Козлов В.Н., Куприянов В.Е., Шашихин В.Н. Управление энергетическими системами. Часть1. Теория автоматического управления
Подождите немного. Документ загружается.


2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
19
Рис. 2.1. Системная классификация линейных моделей ОУ (САУ)
и взаимосвязи между моделями
Важную роль играют интегральные преобразования Лапласа
и Фурье. При этом используются непрерывные преобразования
Лапласа (прямое L и обратное L
-1
преобразования), а также дис-
кретные преобразования Лапласа (прямое DL и обратное DL
-1
преобразования), позволяющие перейти от оригинала к изобра-
жению по Лапласу или от изображения к оригиналу для перемен-
ных, описывающих динамику непрерывных и дискретных объек-
тов и систем. Непрерывное или дискретное преобразования Лап-
Анализ
на основе
ТФКП
Методы
для формы
«вход-выход»
Методы
на основе
формулы Коши
Модели
в виде
«свертки»
Уравнения
состояния
Передаточные
функции
Уравнения
«вход-выход»
Частотные
характеристики
Анализ
на основе
ТФКП
11
,
−−
DLL
DLL, DFF,
11
,
−−
DFF
DL
L
,
1
1
,
−
−
DL
L
DF
F
,
1
1
,
−
−
DF
F

20
ласа позволяют получить модели объектов или систем в виде пе-
редаточных функций или матриц (см. рис. 2.1).
Аналогично применяются прямое непрерывное или прямое
дискретное (
F
или DF ) и обратное непрерывное или обратное
дискретное (
1
−
F
или
1
−
DF ) преобразования Фурье, позволяющие
перейти от оригинала к изображению по Фурье или от изображе-
ния к оригиналу для координат и управлений объекта или систе-
мы. Преобразования Фурье, определяющие частотные характери-
стики непрерывных или дискретных объектов (систем) (см. рис.
2.1), доставляют комплекс соответствующих математических мо-
делей для описания.
2.2. Линейные уравнения «вход–выход»
и ур
авнения «вход–состояние–выход»
Математические модели «вход–выход» для объектов управ-
ления и систем автоматического управления представляются
дифференциальными уравнениями непрерывных объектов (сис-
тем) или конечно-разностными уравнениями дискретных объек-
тов (систем). Эти уравнения связывают линейные комбинации
входных и выходных координат и их производных (для непре-
рывного времени) или входных и выходных координат и их ко-
нечны
х разностей (для дискретного времени). Установление свя-
зей между уравнениями «вход–выход» и уравнениями «вход–
состояния–выход» (уравнениями состояния) – важная задача
моделирования.
2.2.1. Уравнения «вход–выход» и уравнения «вход–
состояние–выход» непрерывных объектов и систем. Связи
между моделями «вход–выход» и уравнениями «вход–состояние–
выход» (уравнения состояния) и способы перехода от од
ной мо-
дели к другой устанавливается с помощью ряда операций.

2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
21
Переход от уравнений «вход–выход» к уравнениям «вход–
состояния–выход». Как показывают приведенные в разд. 1.1
примеры, дифференциальные уравнения непрерывных объектов и
систем могут быть записаны следующим образом:
()
(
)
(
)
(
)
tupBtypA
=
, (2.1)
где
() () ()
(
)
1
() ,, ,,
T
im
yt y t y t y t=
,
() () ()
(
)
1
() ,, ,,
T
ir
ut u t u t u t=
– векторы выходных координат и воздействий (входных коорди-
нат);
()
(
)
gg
g
gg
g
BpBpBpBApApApA +++=+++=
−− 1010
...,...
–
полиномиальные матрицы, причем
0,
0
≠∈
×
ARA
mm
j
,
rm
j
RB
×
∈ и
элементы этих матриц постоянны;
dt
d
p =
– оператор дифферен-
цирования по времени t. При переходе к уравнениям состояния
выполним очевидные преобразования. Перенесем все слагаемые
правой части равенства (2.1) в левую часть и получим:
.0)(
)()(
11
11
1
00
=−+−+
+−+−
−−
−
uByAuByAp
uByApuByAp
gggg
gg
(2.2)
Представим по схеме Горнера полином в левой части (2.2). Тогда
0))...)(((...
11100
=
−
+
−
−
+
−
−
uByA
разg
uBuByAuByAppp
ggg
. (2.3)
В соответствии с формулой (2.3) введем новые переменные
– векторы
i
x
, равные линейным комбинациям переменных в
скобках уравнения (2.3). Тогда получим систему дифференциаль-
ных уравнений:

22
.0
,
..................................
,
,
,
11
1
22
23
11
12
00
1
=−+
−+=
−+=
−+=
−=
−−
−
uByAx
uByAxx
uByAxx
uByAxx
uByAx
gg
g
gg
gg
Решив уравнения относительно y и производных вектора состоя-
ния x, получим алгебраические и дифференциальные уравнения:
,
),(
11
21
0
11
0
uByAxx
uBxAy
+−=
+=
−
.
,
..................................
,
11
1
22
32
uByAx
uByAxx
uByAxx
gg
g
gg
gg
+−=
+−=
+−=
−−
−
Подставим y из первого уравнения в другие уравнения. Тогда
элементарными преобразованиями можно получить уравнения:
.)(
,)(
,)(
,)(
0
1
0
11
0
0
1
011
11
01
1
0
1
022
311
02
2
0
1
011
211
01
1
uBAABxAAx
uBAABxxAAx
uBAABxxAAx
uBAABxxAAx
ggg
g
gg
g
g
g
−−
−
−−
−
−
−
−−
−
−
−+−=
−++−=
−++−=
−++−=

2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
23
Если ввести вектор состояний:
Tgi
xxxx )...,,...,,(
1
=
и матрицы:
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
−
=
−
mmmg
mmmg
mmm
mmm
CA
ECA
ECA
ECA
A
000
00
00
00
1
11
12
11
,
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
−
=
−−
DAB
DAB
DAB
DAB
B
gg
gg 11
22
11
,
,,,),,,(
0
1
0
1
11
BADACOOCC
mm
−
−
=== …
в которых
m
E и
m
O – единичная и нулевая квадратные матрицы
порядка m, то можно получить уравнения «вход-состояния–
выход», известные в литературе как «уравнения состояния»:
DyCxy
B
u
A
x
x
+
=
+
= ,
, (2.4)
где входные координаты – вектор управлений и возмущений.
На основании проведенного анализа можно сформулировать
следующее утверждение.
Утверждение 2.2.1. Если уравнения типа «вход–выход»
имеют вид (2.1), то «вход-состояния-выход» (уравнения состоя-
ния) можно представить в форме (2.4).
Уравнению состояния (2.4) соответствует структурная схема
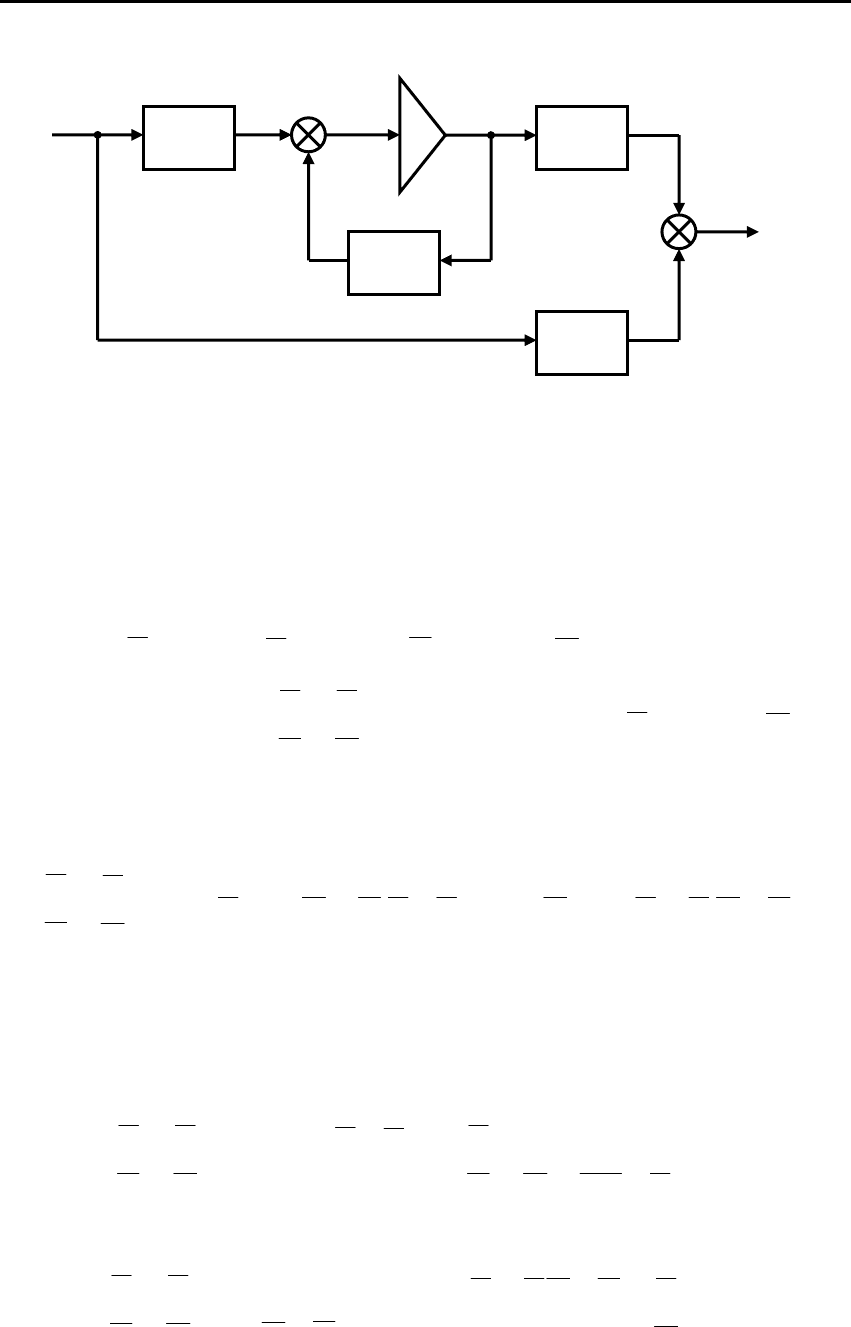
объекта или системы, приведенная на рис. 2.2.
Исследование устойчивости объектов или САУ требует
формирования характеристического полинома объекта или замк-
нутой системы. Наиболее просто характеристический полином
вычисляется для случая, когда ма
трица A – фробениусова, что
будет показано далее. В ряде случаев для определения характери-
стического полинома объекта или системы управления с блоч-
ными матрицами целесообразно использовать лемму Шура.
24
Рис.2.2. Структурная схема для уравнений состояния ОУ (САУ)
Лемма 2.2.1 (лемма Шура о вычислении определителя
блочной матрицы).
Если
mmnmmnnn
RDRCRBRA
×
×
×
×
∈∈∈∈ ,,,
являются
блоками матрицы
⎥
⎦
⎤
⎢
⎣
⎡
=
DC
BA
A
, такими, что 0det,0det
≠
≠ DA ,
то справедливы следующие равенства для определителей:
(
)
(
)
CDBADBACDA
DC
BA
11
detdetdetdetdet
−−
−⋅=−⋅=
⎥
⎦
⎤
⎢
⎣
⎡
.
Последние равенства доказываются приведением исходной
блочной (клеточной) матрицы к квазитреугольному виду
⎥
⎦
⎤
⎢
⎣
⎡
−
=
⎥
⎦
⎤
⎢
⎣
⎡
−
⋅
⎥
⎦
⎤
⎢
⎣
⎡
−
−
BACDC
A
E
BAE
DC
BA
m
n
1
1
0
0
,
⎥
⎦
⎤
⎢
⎣
⎡
−
=
⎥
⎦
⎤
⎢
⎣
⎡
−
⋅
⎥
⎦
⎤
⎢
⎣
⎡
−
−
D
BCDBA
ECD
E
DC
BA
m
n
0
0
1
1
,
B
∫
C
A
D
y
x
x
u

2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
25
и с помощью вычисления определителя квазитреугольной матри-
цы. На основании этого правила определитель квазитреугольной
матрицы равен произведению определителей диагональных под-
матриц. Лемма доказана.
Если коэффициенты характеристического полинома
i
a –
скалярные величины, т.е.
1
Ra
i
∈
, то матрица
A
в уравнениях
«вход-состояния-выход» может иметь «фробениусов вид»:
0
1
2
1
1
000
100
010
001
a
a
a
a
a
A
n
n
⋅
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
−
=
−
.
Применив для вычисления характеристического определителя
правило вычисления «разложением по столбцу или строке» (тео-
рему Лапласа), можно получить характеристический полином
матрицы в виде:
nn
nn
n
aaaAE ++++=−=
−
−
λλλλλχ
1
1
1
)(det)(
,
1
0
=a
,
коэффициенты которого определяются элементами первого
столбца фробениусовой формы матрицы объекта или САУ.
Переход от уравнений состояния к уравнениям «вход–
выход».
Рассматривая обратный переход, ограничимся случаем r
= 1, т.е. будем считать, что в САУ имеется только одно скалярное
управление.
Оператор дифференцирования по времени
d
t
d
p =
вводится
следующим образом:
px
x
=
. Тогда уравнения «вход-состояния-
выход» (2.4) можно записать в следующей форме

26
.)()()(),()()( tDutCxtytButxApE
n
+==−
Решив первое из этих уравнений относительно вектора со-
стояний x(t) и подставив полученный результат во второе уравне-
ние, можно получить окончательное представление вектора вы-
ходных координат системы или объекта управления
)(])([)(
1
tuDBApECty
n
+−=
−
. (2.5)
Напомним, что матрица
)()( AEf
n
−
=
λ
λ
называется ха-
рактеристической матрицей
матрицы А, а матрица, обратная
характеристической
1
)]([
−
λ
f
– резольвентой матрицы А.
Вычислить резольвенту
1
)(
−
− ApE
n
можно на основе сле-
дующего равенства
),(
~
)(
1
)(
1
pB
p
ApE
n
n
χ
=−
−
(2.6)
в которой )(
~
pB – матрица, присоединенная к матрице f(p), т.е.
матрица, транспонированная по отношению к матрице алгебраи-
ческих дополнений элементов f(p).
В соответствии с этим присоединенная матрица
)(
~
pB
при-
нимает вид:
12
12 1
() ,
nn
nn
Bp Bp Bp B p B
−−
−
=+ +++
где
i
B
~
– числовые квадратные матрицы порядка n, причем мат-
рица
1 n
BE=
.
Представим характеристический полином
)( p
n
χ
матрицы А
в стандартном виде:
.)(
1
1
1 nn
nn
n
apapapp +++=
−
−
χ

2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
2
7
Заметим, что разность
)()( qp
nn
χ
χ
−
делится на (p–q) без остатка
так, что полином:
,1,)(
)(
)()(
),(
01
2
1
13
21
2
2
1
1
=+++=++++
+++=
−
−
=Δ
−
−−−
−−
bbpbppaqaq
paqp
qp
qp
qp
n
nnn
nn
nn
……
χ
χ
является многочленом относительно p и q . Коэффициенты этого
полинома можно вычислить по рекуррентному соотношению:
,1,1,
1
−=+=
−
nkabqb
kkk
причем 0
1
=+
− nn
abq .
Рассмотрим тождество
),()()()( qpqpqp
nn
Δ⋅
−
=
−
χ
χ
, кото-
рое справедливо, если вместо p и q в него подставить перестано-
вочные матрицы
n
pE и А, соответственно. После такой подста-
новки будем иметь следующее равенство:
()(,)( )
nn n n
pE pE A pE A
χ
=Δ − . При доказательстве использована
теорема Гамильтона–Кели, на основании которой всякая квад-
ратная матрица удовлетворяет своему характеристическому
уравнению
.0)( =A
n
χ
Если переписать соотношение (2.6) в виде
)()(
~
)( A
n
pEpB
n
Ep
n
−=
χ
и сравнить его с ранее полученным представлением, то можно
придти к следующему результату:
),()(
~
ApEpB
n
Δ= .
Выполним переход от скалярных переменных p и q к матри-
цам
n
pE и A в рекуррентной формуле, а также заменим скаляр-
ные коэффициенты
k
b матричными –
k
B
~
.
28
Тогда можно получить следующую совокупность рекур-
рентных соотношений:
1
,2,; 0.
kkkn nnn
BAB aE k nABaE
−
=+ = +=
Обратимся далее к формуле Ньютона:
11 11
,1,,
kkk k
ka s a s a s k n
−−
=− − − − =
для вычислния коэффициентов
k
a характеристического полино-
ма. В формуле использовано следующее обозначение для следа
матриц A
k
:
∑
==
=
n
i
k
i
k
k
trAs
1
λ
Подставим
k
s
в формулу Ньютона для .1
=
k Тогда будем
иметь следующее равенство:
)(
11
Atrsa
−
=
−
=
.
Для 2=k можно получить равенство:
2211 1 1
11 1
() (( )) ().
22 2
n
a s a s tr A A a E tr AB=− + =− + =−
При 3=k будем иметь:
2
231221 12
12 2
11
()(( ))
33
11
(( )) ( ).
33
n
n
asasastrAAaAaE
tr A AB a E tr AB
=− + + =− + + =
=− + =−
Продолжив этот процесс, можно получить окончательные фор-
мулы для вычисления коэффициентов характеристического по-
