Козлов В.Н., Куприянов В.Е., Шашихин В.Н. Управление энергетическими системами. Часть1. Теория автоматического управления
Подождите немного. Документ загружается.

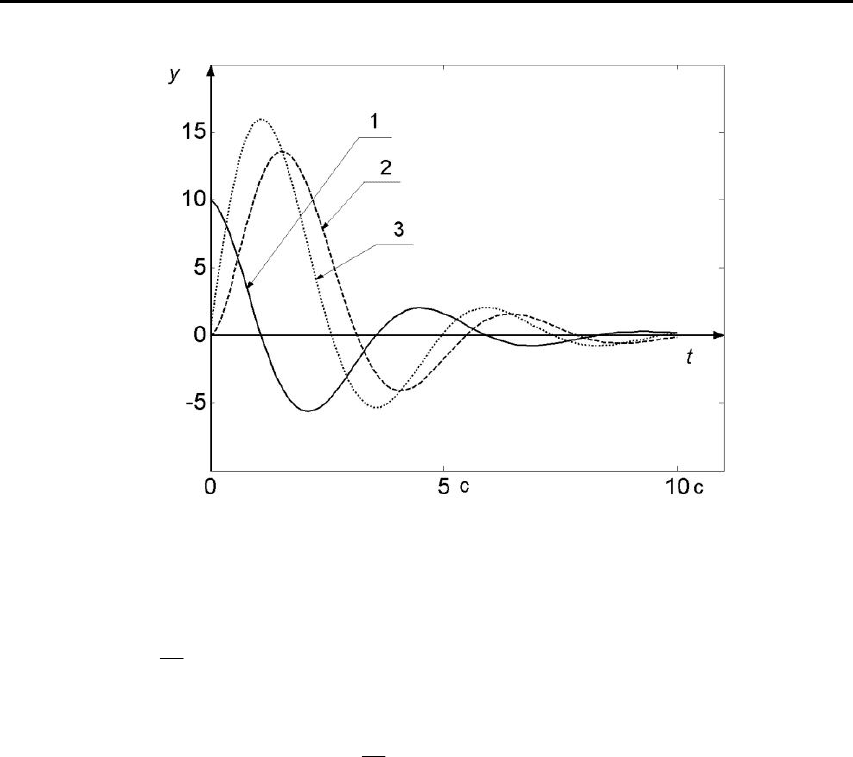
2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
49
Рис. 2.3. Переходные процессы в ОУ третьего порядка
начальных условиях, нулевом возмущении и единичном управле-
нии
))(1,0( tU ==
μ
- зависимость «2»; переходный процесс с ну-
левыми начальными условиями, единичном возмущении и нуле-
вом управлении: (
)0),(1 == Ut
μ
- зависимость «3».
2.3.2. Анализ процессов в дискретных объектах и систе-
мах.
Рассмотрим методику решения уравнений (2.11) дискретных
ОУ и САУ. Эти уравнения имеют вид
.,,
0
01
xxDuCxyBuAxx
tttttt
=+=+=
+
(2.23)
Анализ динамики дискретных объектов (систем) основан на
приведении матрицы А к канонической форме Жордана (как и в
случае непрерывных объектов). С этой целью используется
пре-
образование подобия
:
tttt
xSzSzx
1
,
−
== и приведение уравне-
ний состояния (2.23) к следующей форме:
1
1
,,
tt tt tt
zJzSBuyCSzDu
−
+
=+ = + (2.24)

50
причем
AS
S
J
1−
= – каноническая форма Жордана для матрицы
А. Можно убедиться, что первому уравнению системы (2.23) при
0
0
xx = удовлетворяет функция дискретного аргумента
t
:
,,,
0
1
0
1
0
110
xSzSzxBuSJzJz
tt
t
h
h
htt
t
−
−
=
−−−
==+=
∑
(2.25)
которая является формулой Коши для неоднородных конечно-
разностных уравнений
объектов (систем). Если перейти к мо-
менту времени (t+1), то можно получить равенство для исследо-
вания переходных процессов в дискретном времени
.
11
1
0
110
0
101
1
ttt
t
h
h
htt
t
h
h
htt
t
BuSJzBuSBuSJzJJ
BuSJzJz
−−
−
=
−−−
=
−−+
+
+=+
⎥
⎦
⎤
⎢
⎣
⎡
+=
=+=
∑
∑
Формула (2.25) представляет общее решение конечно-
разностного уравнения (2.24).
Степени квазидиагональной матрицы Жордана определяют-
ся равенствами
]...,,,[diag
10
t
s
ttt
JJJJ =
,
где
1
1
2
1
0
00
0
00
,.
0
00
0
t
t
i
t
t
tt
i
i
t
t
p
ik
J
J
JJ
J
λ
λ
λ
⎡⎤
⎡
⎤
⎢⎥
⎢
⎥
⎢⎥
⎢
⎥
==
⎢⎥
⎢
⎥
⎢⎥
⎢
⎥
⎢⎥
⎢
⎥
⎣
⎦
⎣⎦

2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
51
Пусть
ij
J
–
j-я клетка h -го размера i -го «ящика» Жордана, ко-
торая может быть представлена в виде суммы:
(1)
ij i h
h
J
EI
λ
=+,
где
)1(
h
I – первый единичный «косой ряд» h -го размера, имею-
щий единицы в первой «наддиагонали»
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
0000
1000
0100
0010
)1(
h
I
и обладающий свойством:
⎩
⎨
⎧
≥
<
=
.при,0
,при,
)(
)(
)1(
hl
hlI
l
I
l
h
h
.
Матрицы
)(l
h
I – имеют единицы в l -ой «наддиагонали». Тогда
степень «клетки» при
h
t
≥ определяются равенством:
∑
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=+=
−
=
−
1
0
)(
)1(
)(
h
l
l
h
lt
t
h
hi
t
I
i
l
t
IE
ij
J
λλ
.
Решения (2.19) и (2.25) используются при анализе переход-
ных процессов в непрерывных и дискретных САУ, а также для
исследования переходных и частотных характеристик дискрет-
ных обьектов и систем управления.
Пример 2.3.4. а). Рассмотрим переход от математической
модели непрерывного объекта управления, заданной в простран-
стве cостояний, к дискретной модели. Сформируем уравнения
электроэнергетического объединения, рассмотренного ранее, для
дискретного времени
h
t
k
/= :

52
).()()(),()()1( kuDkxCkykuBkxAkx
дд
+=+=+
Очевидно, что матрицы C и D этой модели совпадают с соответ-
ствующими матрицами непрерывной модели. Выбрав величину
шага
h
достаточно малой (такой, чтобы входные воздействия на
этом интервале можно было считать постоянными) и заменив в
соотношении (2.15)
0
x
на ()
x
kh , ()
x
t на (( 1) )
x
kh
+
, получим
0
,.
h
Ah A
gg
A
eBed
τ
τ
==
∫
Учитывая ранее полученные соотношения для
tA
e и при
ch 01.0= , вычислим матрицы уравнений состояния в дискретном
времени:
.
001.0014.1
0020.0
250.0002.0
,
1001.0009.0
0980.0001.0
012.0247.0998.0
1
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
=
−
==
д
B
S
Jh
eS
Ah
e
д
A
б). Переход к модели «вход–выход». Уравнение «вход–
выход» для данной дискретной системы можно задать в виде:
[] [] []
[] [][]
,)(
3
)(
2
)(
2
1
)(
3
)(
2
)(
2
1
)(
3
kubkubkub
kyakyakyaky
++=
=+++
ξξ
ξξξ
(2.26)
где
ξ
– оператор сдвига вперёд, а коэффициенты
i
a
,
i
b
вычисля-
2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
53
ется по формулам, аналогичным формулам для непрерывных
систем (2.8). Используя представление резольвенты
)(
)(
1
1
)(
ξ
ξχ
ξ
B
n
A
n
E
g
=
−
−
, где
)(
ξ
χ
n
– характеристический по-
лином матрицы
A
,
32
2
1
)( BBBB ++=
ξξξ
– полиномиальная
матрица, определение которых было рассмотрено ранее, получим
д
BCBb
11
=
,
,
22 д
BCBb
=
д
BCBb
33
=
.
Согласно алгоитму п. 2.2, резольвенту системы можно опреде-
лить следующими равенствами:
,978.2)(,
100
010
001
1131
−=−=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
==
д
ABtraEB
),250.0002.0(
11
=
=
д
BCBb
,
978.1001.0009.0
0998.1001.0
012.0247.0980.1
3112
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−−
−
−
=+= EaABB
д
,956.2)(
2
1
22
=−=
д
ABtra ),495.0011.0(
22
−
−
=
=
д
BCBb
,
978.0001.0009.0
0998.0001.0
012.0247.0980.0
3223
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
=+= EaABB
д
,978.0)(
3
1
33
−=−=
д
ABtra .)245.0009.0(
33
−
=
=
д
BCBb

54
При подстановке вычисленных коэффициентов в уравнение
(2.26) можно получить модель объекта или системы управления
типа (2.13) для дискретного времени, которая представляется
разностным уравнением:
[]
[]
.)(245.0)(009.0)(495.0)(011.0
)(25.0)(002.0
)()()()(
2
32
2
1
3
kkUkkU
kkU
kyakyakyaky
μμξ
μξ
ξξξ
++−−+
++=
=+++
Последнее уравнение является моделью типа «вход-выход»
(полиномиальной моделью) дискретного объекта или системы,
которое используется при анализе и синтезе объектов и систем
управления.
2.4. Уравнения свертки и импульсные переходные функции
«Модели в виде свертк
и»
для линейных объектов и систем
управления можно определить из аналитических решений, опре-
деляемых формулой Коши, для линейных уравнений состояния.
2.4.1. Уравнения свертки для непрерывных объектов
или систем.
Рассмотрим реакцию линейной системы на входное
воздействие
)(
t
u , определяемую формулой Коши (2.15) при ну-
левых начальных условиях. Тогда для анализа процессов можно
использовать равенства:
).()()(,)()(
0
)(
tuDtxCtydBuetx
t
tA
+==
∫
−
ττ
τ
(2.27)
Ситуация, когда при t < 0 на систему не воздействуют внешние
возмущения, а начальные условия нулевые, типична для многих

2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
55
вариантов работы систем. Введем специальную функцию вре-
менного аргумента:
⎪
⎩
⎪
⎨
⎧
<
≥
=
.0,0
0,
)(
t
tB
At
e
tw
(2.28)
Тогда формула (2.27) с учетом (2.28) определит уравнение
свертки
, в котором правая часть задается интегралом свертки:
() ( ) ( ) () () ()
0
,.
t
x
twu wt ud ytCxtDut
τττ
=∗= − = +
∫
(2.29)
Определение 2.4.1. Функция (2.28) называется импульсной
(весовой) функцией или импульсной переходной функцией
(ИПФ).
Учитывая, что u(t) приложено в момент t = 0 и управление
⎪
⎩
⎪
⎨
⎧
≥
<
=
,0),(
,0,0
)(
ttu
t
tu
формулу (2.29) можно записать в виде
).()()(
,)()()()()(
1
00
11
tDtwCtw
dtutwdutwty
tt
δ
τττττ
+=
∫∫
−=−=
(2.30)
Содержательный смысл ИПФ можно определить, если считать,
что управление –
δ-функция (функция П. Дирака), определяемая
равенствами:
1)(
,0,0
,0,
)( =
⎩
⎨
⎧
≠
=∞+
=
∫
∞
+
∞
−
dtt
t
t
t
δδ
.

56
Фильтрующее свойство δ-функции, математически опреде-
ляемое
интегралом свертки: )()()( tfdtf =
∫
−
∞
+
∞
−
ττδτ
, позволяет
получить равенства:
).()()()(),()()()(
1
0
twtDtCwtytwdtwtx
t
=+==−=
∫
δττδτ
(2.31)
Из равенств (2.31) следует, что ИПФ - реакция на входное воз-
действие, равное δ-функции
, приложенное к объекту или систе-
ме управления при t = 0. Вычисление ИПФ можно выполнить с
помощью алгоритма, основанного на приведении матрицы урав-
нений состояния к форме Жордана (см. п.2.3).
Пример 2.4.1. Нетрудно видеть, что ИПФ объекта управле-
ния, рассмотренного в примере 2.3.2:
==
−
BSeStw
Jt 1
)(
,
32
0
66
1
0
0
020
622
201
00
0
00
5.05.01
5.000
113
2
2
2
22
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
+−
−
=
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−−
−−
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−−
−
−
=
−−
−−
−
−−
−
tt
tt
t
tt
t
ee
ee
e
tee
e
).(6)()(
2
1
tt
eetwCtw
−
−
−=⋅=
Полученные равенства можно использовать далее для по-
строения других типов моделей, в частности, моделей в виде

2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
5
7
матриц часточных характеристик и передаточных функций (мат-
риц).
2.4.2. Уравнения свертки для дискретных объектов и
систем.
Введем понятие ИПФ для дискретных систем на основе
формулы Коши (2.25), определяющей реакцию линейной систе-
мы на входное воздействие
t
u
при нулевых начальных условиях:
n
x 0
0
= . Тогда
.,
1
0
1
ttt
t
l
l
lt
t
uDxCyuBAx +=
∑
=
−
=
−−
(2.32)
Если ввести функцию дискретного аргумента так, что
⎩
⎨
⎧
<
≥
=
,0,0
,0,
t
tBA
w
t
t
(2.33)
то формула (2.32) примет вид
,
1
0
,
1
ttt
t
l
lltt
uDxCyuwuwx +=
∑
=∗=
−
=
−−
(2.34)
где функция (2.33) называется ИПФ дискретных ОУ или САУ.
Вычисление ИПФ можно (как и для непрерывных объектов и сис-
тем) выполнить с применением форм Жордана (2.17).
Модели объектов и систем в виде уравнений свертки ис-
пользуются при анализе переходных процессов и входо-
выходной устойчивости объектов или систем автоматического
управления.
Пример 2.4.2. Рассмотрим методику построения переходно-
го процесса при нулевых начальных условиях на основе уравне-
ния свертки для объекта, рассмотренного в примере 2.3.3. Урав-
нение свертки для рассматриваемого объекта имеет вид:

58
,)()()()()(
0
τττ
dutwtutwtx
t
∫
−=∗=
где
23
)(
×
∈ Rtw – матричная импульсная переходная функция:
(
)
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
−
=
)(
32
)(
31
)(
22
)(
21
)(
1211
1
)(
twtw
twtw
twtw
BS
Jt
eStw
,
1, 3
1,3
{} ,
j
ij
i
Ss
=
=
=
{
}
3,1
3,1
~
1
=
=
=
−
j
i
ij
SS
, ),,diag(
3
21
t
e
t
e
t
e
Jt
e
λ
λ
λ
= ,
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
00
02
250
B
была ранее определена в приведенном выше примере 2.3.3. То-
гда, учитывая диагональную форму
Jt
e
, элементы матрицы S и
значения элементов
B , можно получить соотношения для эле-
ментов импульсной переходной функции рассматриваемой сис-
темы:
[]
,576.25)325.1sin(672.20)325.1cos(576.25
)
~
~
~
()(
298.14136.0
3213
3
2212
2
1211
1
21
11
tt
t
tt
ette
SSeSSeSSebtw
−−
−+=
=++=
λ
λ
λ
[]
,981.8)325.1sin(546.0)325.1cos(981.33
)
~
~
~
()(
298.14136.0
3113
3
2112
2
1111
1
12
12
tt
t
tt
ette
SSeSSeSSebtw
−−
−−=
=++=
λ
λ
λ
[]
,185.2)325.1sin(937.0)325.1cos(185.0
)
~
~
~
()(
298.14136.0
3223
3
2222
2
1221
1
2121
tt
t
tt
ette
SSeSSeSSebtw
−−
++−=
=++=
λ
λ
λ
