Козлов В.Н., Куприянов В.Е., Шашихин В.Н. Управление энергетическими системами. Часть1. Теория автоматического управления
Подождите немного. Документ загружается.


2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
99
вующие процедуры для линейных систем. Эти схемы могут ис-
пользоваться при анализе и синтезе в качестве дискретных анало-
гов непрерывных линейных и кусочно-линейных дифференци-
альных систем, представляющих модели объектов управления.
Таким образом, рассмотренные разностные схемы и мето-
дика доказательства устойчивости кусочно-линейных разностных
схем позволяет исследовать определенные классы разностных
схем для кусочно-линейных дифференциальных уравнений.
2.9.4. Теорема о сравнении решений. При анализе объек-
тов (систем) управления возникает классическая
проблема срав-
нения решений
- оценки нормы оценки разности решений исход-
ной (нелинейной) системы уравнений и аппроксимирующей (ку-
сочно-линейной) системы. Степень отличия решений при ап-
проксимации можно оценить на основе традиционных или обоб-
щенных теорем сравнения.
Обобщенные теоремы сравнения
решений используется для оценки нормы отклонений решений
в функциональных пространствах. Сущность обобщения состоит
в том, что искомая оценка отклонений норм решений двух систем
сводится к квадратурам, заданным на решениях линейных (базо-
вых) дифференциальных уравнений. При доказательстве обоб-
щенной теоремы сравнения будет использована лемма.
Лемма Грoнуола. Пусть
1
)( RXf ∈
- непрерывная функция
на интервале
1
0
),( RXX ∈
такая, что:
0)( ≥Xf
. Кроме этого:
∫
+≤≤
X
X
dfXf
0
)()(0
ξξμλ
, где
0,0 >≥
μ
λ
, причем
λ
и
μ
- кон-
станты. Тогда имеет место следующая оценка:
0
)(
XX
Xf
−
≤
μ
λε
.
Теорема 2.9.4 (обобщенная теорема сравнения решений).
Пусть имеются две системы дифференциальных уравнений объ-
ектов или систем с непрерывными правыми частями:
1).
Исходная нелинейная система:

100
))(),((),(
~
UXFUXFX
UX
ΦΦ==
•
,
2). Аппроксимирующая кусочно-линейная система:
)()( uBxAx
ux
Φ+Φ=
•
,
правые части которых удовлетворяют условию Липшица с посто-
янной
L
. Тогда если
)(tX
- решение первой системы с началь-
ными данными
()
)(,
00
tXt
, а
)(tx
- решение кусочно-линейной
системы с такими же начальными данными, то оценка отклоне-
ний решений для
01
[,]ttt∈ по норме:
01
1,..., [ , ]
|| ( ) || max max | ( ) |
i
inttt
zt z t
=∈
=
имеет вид:
∫
+−−
≤
≤
−
+
−
≤−
t
t
duByAUyF
t
y
t
x
t
y
t
X
t
x
t
X
0
||)()),((
~
||
[
||)()(||||)()(||||)()(||
τττ
(2.69)
∫
−
−−Φ+Φ+
t
t
ttL
ux
o
eduByAUByA
0
||
]||)()())((||
τττ
где
()
ty
- решение линейной (третьей) системы сравнения
uByAy +=
с липшицевой правой частью с константой
L
.
Доказательство. Эквивалентные интегральные уравнения
систем, решения которых будут сравниваться между собой:
1). Исходной нелинейной системы:

2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
101
∫
+=
t
t
dUXFtXtX
0
,))(),(()()(
~
0
τττ
2). Аппроксимирующей кусочно-линейной системы:
() ( ) ( )() ()()()
∫
Φ+Φ+=
t
t
ux
duBxAtxtx
0
0
τττ
3). Линейной системы сравнения:
() ( ) () ()
(
)
∫
++=
t
t
duByAtyty
0
0
τττ
.
Разность решений рассматриваемых дифференциальных систем
уравнений в силу соответствующих эквивалентных интегральных
уравнений можно представить с помощью вычитания уравнений
соотношениями:
()
(
)
(
)
(
)
(
)
(
)
()
()(
) () ()
()
( )
(
)
()
(
)
(
)(
)
(
)
(
)
.
,
~
00
0 0
∫
∫
∫
∫
Φ
+
Φ
−
+ +
+
+
−
=
=
−
+
−
=
−
t
t
u
x
t
t
t
t
t
t
d
u
B
x
A
d
B
y
A
d
u
B
y
A
d
U
X
F
t
x
t
y
t
y
t
X
t
x
t
X
τ
τ
τ
τ
τ
τ
τ
τ
τ
τ
τ
τ
Оценка нормы разности
(
)
(
)
txtX
−
, элементарные преобра-
зования и аксиома треугольника позволяют определить совокуп-
ность оценок для норм разности решений дифференциальных
систем:
(
)()
(
)
(
)
(
)
(
)
=−+−≤− tytxtytXtxtX
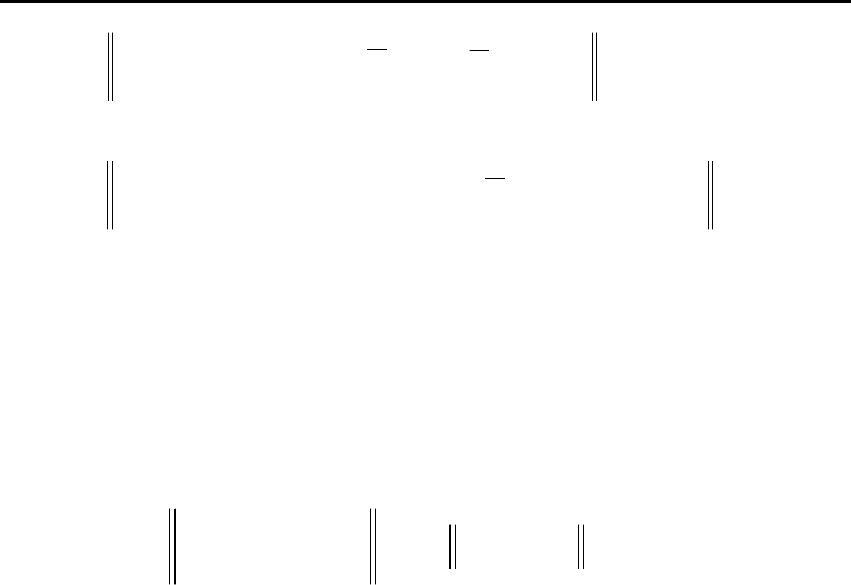
102
() ()()() ()
()
(
)
()() ()() () ()
()()
∫
∫
+−Φ+Φ+
++−=
t
t
ux
t
t
dBuyAuBxA
duByAUXF
0
0
,
~
τττττ
τττττ
при равенстве начальных условий:
(
)
(
)()
000
tytxtX
=
=
. Добавле-
ние и вычитание вектор-функции
(
)
(
)
(
)
ττ
uyF ,
~
к подынтеграль-
ному выражению первого интеграла и вектор-функции вида
()() ()
(
)
τ
τ
uByA
ux
+Φ
второго интеграла, учет условия:
()() ()()
∫∫
≤
t
t
t
t
dXfdXf
00
ττττ
и применение аксиомы треугольника для подынтегральных вы-
ражений в последних соотношениях приводит к оценке нормы
для рассматриваемых отклонений решений сравниваемых урав-
нений следующего вида:
.||]))}(())(({))(())((||
||))}(())(({))(())(([||
||]))}()({))(),((||
||))(),((())(),(([||||)()(||
~
~~
τττττ
ττττ
τττττ
ττττ
duФByФAuBФyAФ
uBФyAФuBФxAФ
duByAUyF
UyFUXFtxtX
uxux
t
t
uxux
t
t
o
o
−−
−−
+−++
++−++
++−+
+−≤−
∫
∫
После применения условия Липшица для норм в подинтеграль-
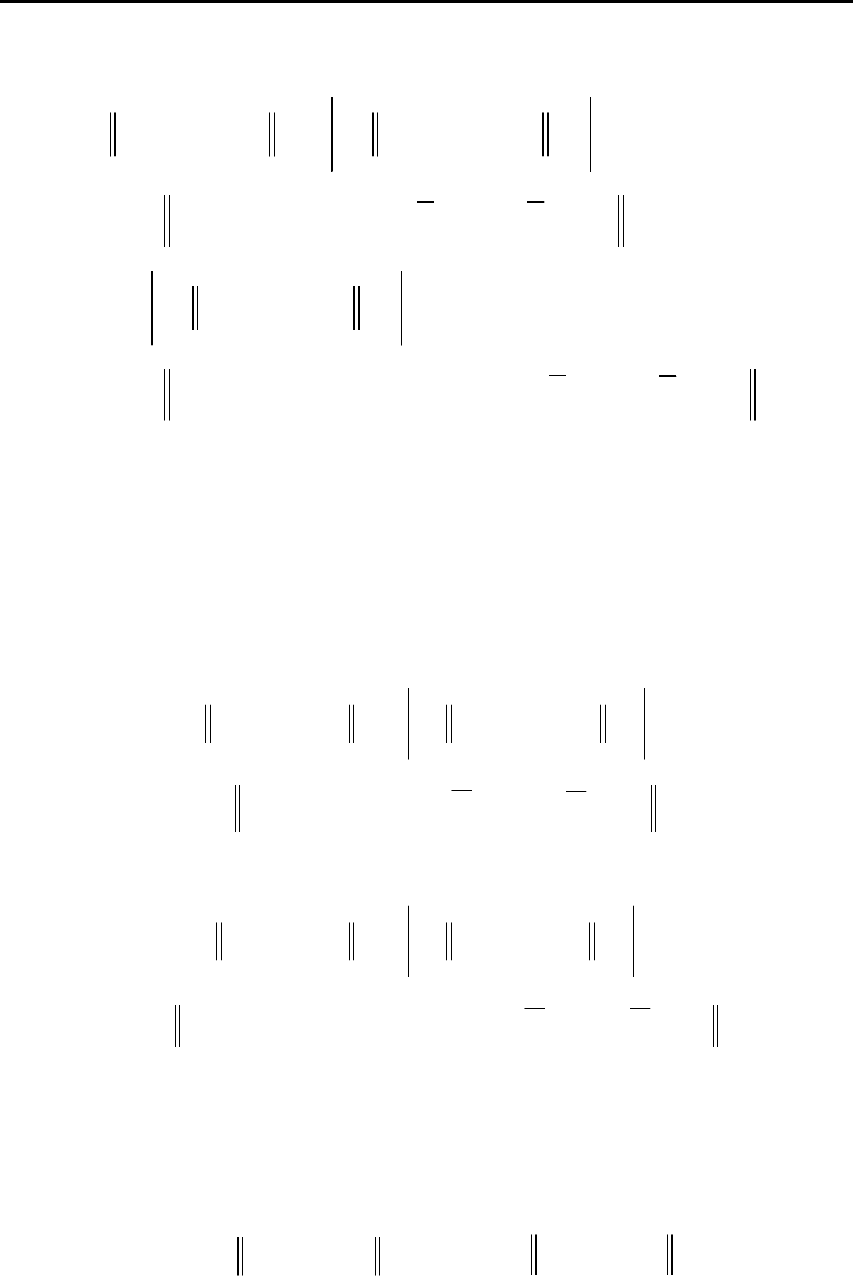
2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
103
ных функциях последнего неравенства оценка принимает вид:
() () () ()
() ()
()
() ()
()
() ()
()
()
()
()
() ()
()
0
0
0
0
,
.
t
t
t
t
t
t
t
xu
t
Xt xt L X x d
Fy U Ay Bu d
Lx yd
AФ yBФ uAyBud
τττ
ττ τ ττ
τττ
τ
ττττ
−≤ − +
+−++
+−+
++−+
∫
∫
∫
∫
Последнее неравенство можно рассматривать как сумму
двух неравенств, которые следуют из рассмотрения полученных
интегралов. В результате можно получить оценки нормы откло-
нений решений (координат) исходной и кусочно-линейной сис-
тем в следующем виде:
() () () ()
() ()()()
()
()
() () () ()
()() ()() () ()
()
∫
∫
∫
∫
+−Φ+Φ+
+−≤−
+−+
+−≤−
t
t
ux
t
t
t
t
t
t
duByAuByA
dyxLtytx
duByAUyF
dyXLtytX
o
0
0
0
.
,),
~
τττττ
τττ
τττττ
τττ
Для каждого из последних неравенств справедлива оценка,
следующая из леммы Гронуола, поскольку
()
(
)
0
1
≥−= tytXf
,
(
)
(
)
0
2
≥−= tytxf
.
Поэтому применение леммы Гронуола доказывает утвер-
ждение обобщенной теоремы сравнения. Применение доказанной

104
теоремы позволяет получить оценки отклонений решенй для раз-
личных моделей, используемых при анализе и синтезе и условий
функционирования объектов и систем.
2.10. Нелинейные математические модели объектов и систем
c распределенными параметрами
Методы анализа процессов в нелинейных объектах и систе-
мах с распределенными параметрами будут рассмотрены на при-
мере моделей теплопроводности. Уравнения в частных производ-
ных будут представлены кусочно-линейными уравнениями теп-
лопроводности, а задача исследования переходных процессов
сформулирована как задача Коши или краевая задача.
2.10.1. Кусочно-линейные уравнения теплопроводности
и основные задачи.
Для процессов с сильными изменениями
свойств теплопроводности имеет смысл сформулировать разно-
стные схемы для одной из канонических форм уравнений. В этих
уравнениях изменение характеристик теплопроводности учиты-
вается кусочно-линейными функциями от первых производных
температуры по времени так, что уравнения имеют вид
()
.Tt,x,t,xf
x
u
)
t
u
( <<<<+
∂
∂
=
∂
∂
010
2
2
1
Φ
(2.70)
Кусочно-линейный оператор от первой производной температу-
ры по времени в (2.70) учитывает изменение параметров тепло-
проводности как функции скорости изменения температуры. Ес-
ли оператор левой части монотонный, то возможны обобщения
методики на случай кусочно-линейной правой части уравнения
теплопроводности.
Задача Коши для данного уравнения теплопроводности –
вычисление его решения при заданных начальных условиях:
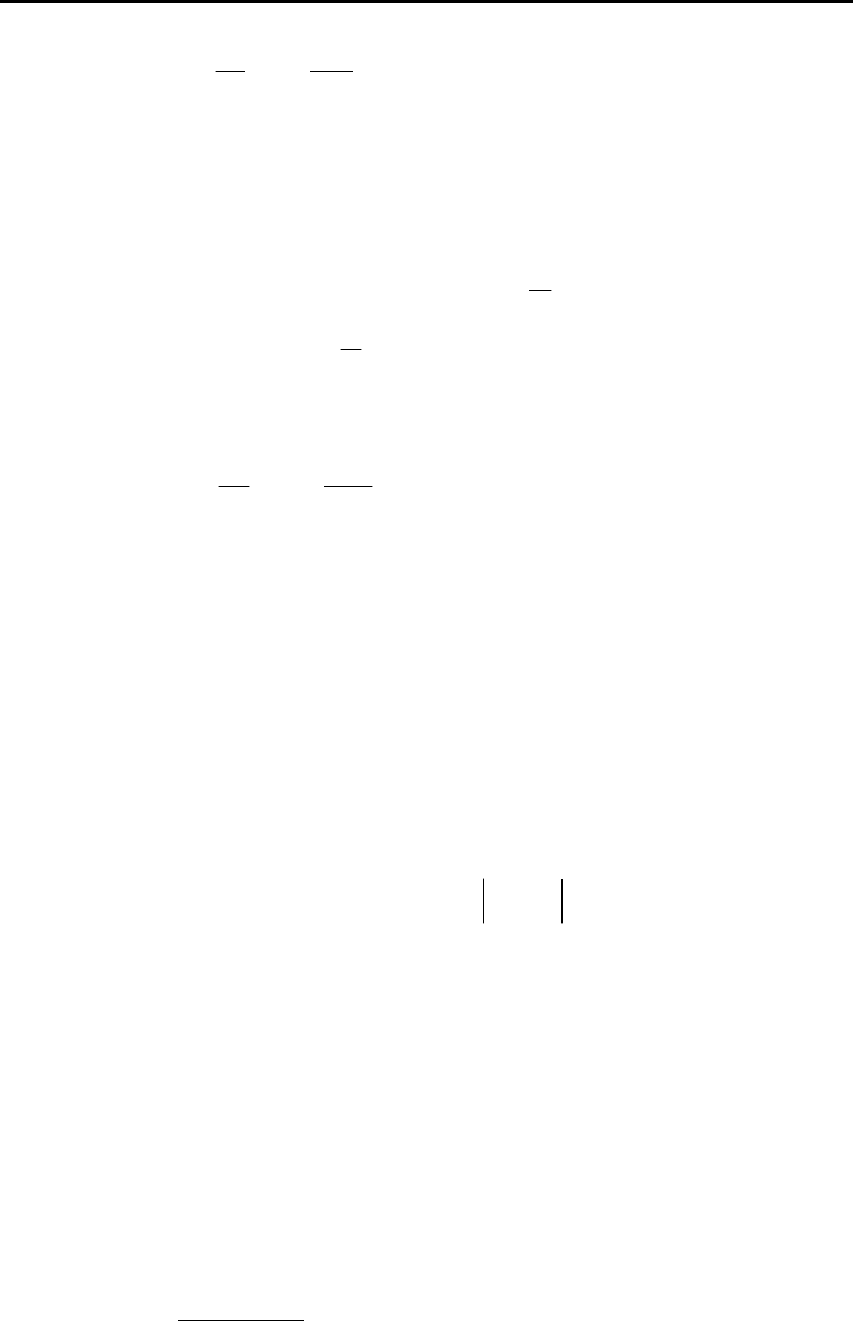
2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
105
()
() ()
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎬
⎫
≤≤=
<<<<+
∂
∂
=
∂
∂
.x,xu,xu
,Tt,x,t,xf
x
u
)
t
u
(
100
010
0
2
2
1
Φ
(2.71.а)
На основе (2.70) и краевых условий можно сформулировать так-
же краевую задачу в прямоугольнике
(
)
Tt,xD ≤≤
≤
≤
=
010
: найти
непрерывное в области
D решение
(
)
t,xuu
=
краевой задачи
()
() ()
( ) () ( ) ()
⎪
⎪
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎪
⎪
⎬
⎫
≤≤==
≤≤=
<<<<+
∂
∂
=
∂
∂
.Tt,tut,u,tut,u
,x,xu,xu
,Tt,x,t,xf
x
u
)
t
u
(
0
2
1
1
0
10
0
0
010
2
2
1
Φ
(2.71.б)
В уравнениях (2.70), задаче Коши (2.71.а) и краевой задаче
(2.71.б) используются кусочно-линейные операторы
10
1
( ) , ,
s
ppр k
p
yzbz zqqqpk
αα
=
=Φ = + + − > >
∑
, (2.72)
которые позволяют учесть изменяющиеся свойства среды.
2.10.2. Основное соотношение и разностные схемы. Ос-
новные разностные схемы для одномерных уравнений могут
быть сформулировны дискретизацией по времени и пространст-
ву. В результате можно получить однопараметрическое семейст-
во кусочно-линейных разностных схем для (2.70) и задач (2.71):
j
i
φ
j
i
y)σ(
j
i
yσ)
τ
j
i
y
j
i
y
( +−+
+
=
−
+
ΛΛΦ
1
1
1
1
, (2.73)

106
где
j
i
y
- сеточная функция для функции
(,)uxt
, причем
i
- сеточ-
ный аргумент для пространственной координаты
x
, а
j
- для
времени; - оператор вычисления второй разности температуры
по
x
. На основе (2.73) формулируются разностные схемы с по-
мощью исчисления кусочно-линейных операторов.
Явные кусочно-линейные разностные схемы. Для уравне-
ний (2.70) из разностной схемы (2.73) при σ = 0 следует кусочно-
линейный аналог «четырехточечной» разностной схемы:
j
i
φ
j
i
y)
τ
j
i
y
j
i
y
( +=
−
+
ΛΦ
1
1
. (2.74)
Применение к обеим частям (2.74) обратного оператора и преоб-
разования определяют явную «четырехточечную» схему:
.
)
j
i
φ
j
i
y(τ
j
i
y
j
i
у +
−
+=
+
ΛΦ
1
1
1
(2.75)
Из (2.75) следует окончательный вид явной разностной схемы:
,
j
i
φh
j
i
y
j
i
y
j
i
yτ
j
i
y
j
i
у
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+−
−
−
+=
+
2
1
2
1
1
1
1
Φ
(2.76)
где
()
qz =Φ
−1
1
– обратный кусочно-линейный оператор, вычисляе-
мый с применением леммы об обращении кусочно-линейных
операторов.
Неявные и частично-неявные кусочно-линейные разно-
стные схемы.
При 0
≠
σ
неявная схема для уравнения
()
f
x
x
u
t
u +=
1
Φ
принимает вид:
()
j
i
φ
j
i
yσ
j
i
yσ
τ
j
i
y
j
i
y
+
⎟
⎠
⎞
⎜
⎝
⎛
−+
+
=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
+
1
1
1
1
ΛΦ
. (2.77)
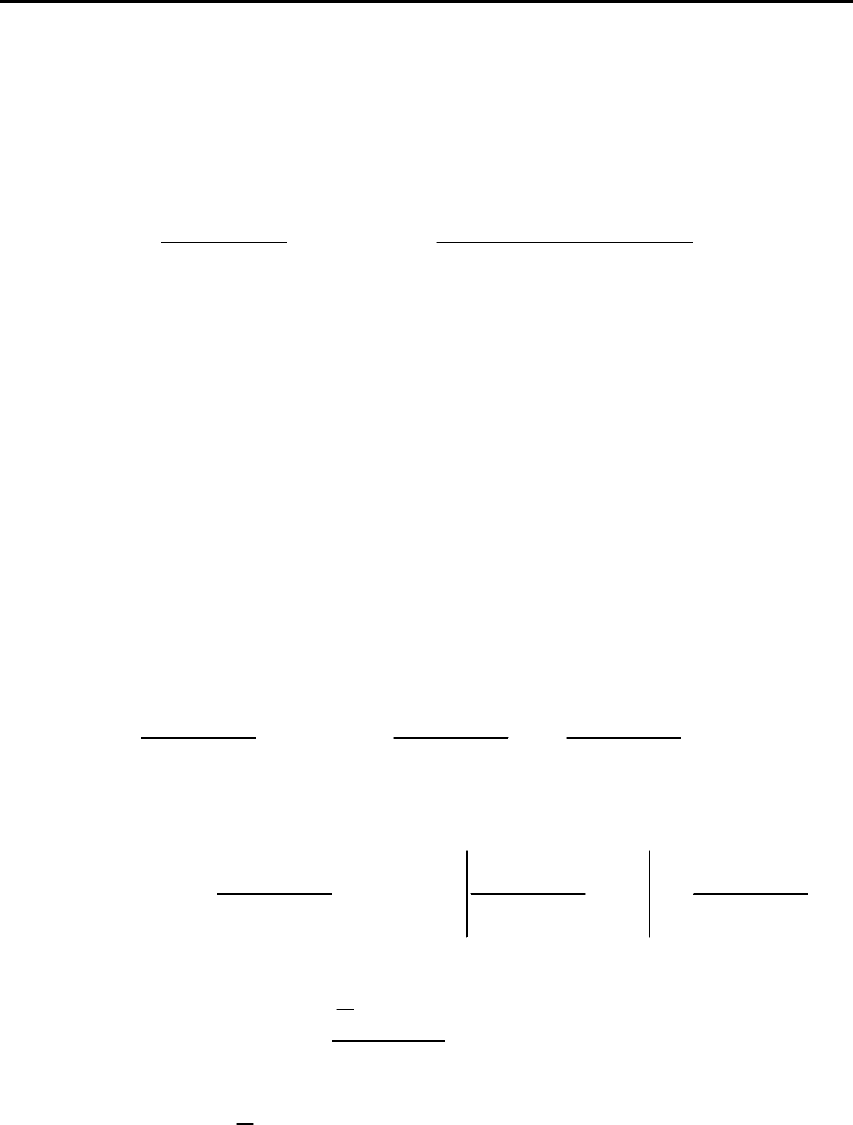
2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
10
7
Из уравнения (2.77) при
1
=
σ
определяется схема с опережением
или чисто
неявная разностная схема для кусочно-линейного
уравнения:
j
i
φ
h
j
i
y
j
i
y
j
i
y
j
i
y
τ
j
i
y
j
i
y
+
+
+
+
−
+
−
=
+
=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
+
2
11
2
1
1
1
1
1
ΛΦ
. (2.78.а)
Проблема построения семейства кусочно-линейных разно-
стных схем на основе общего вида неявных схем сводится к раз-
решимости алгебраических кусочно-линейных уравнений
(2.78.а), что в общем случае приводит к определенным трудно-
стям. Объем вычислений при формулировке однородных схем
сокращается при переходе к частично-неявным разностным схе-
мам. С учетом (2.72) уравнение (2.78.а) п
реобразуется к следую-
щему виду:
111
11
2
111
2
0
1
j1
2
,
jj jj jj
ii ii ii
jj jj jj
s
ii ii ii
pp
p
j
j
ii
i
yy yy yy
h
yy yy yy
bq
h
yy
h
ττ
αα
ττ
ϕ
+++
Δ
+++
=
+
⎛⎞⎛⎞
−−−
Ψ=Φ−=
⎜⎟⎜⎟
⎝⎠⎝⎠
⎛⎞
−−−
=+ + − − =
⎜⎟
⎝⎠
−
=+
∑
где переменные
1
j
i
y
+
вычисляются с помощью явных разностных
схем типа (2.76). Применение обратного оператора ψ
-1
к обеим
частям последнего равенства определяет частично-неявную ку-
сочно-линейную разностную
схему «предиктор-корректор»
первого типа
, которая определяется совокупностью соотноше-
ний:
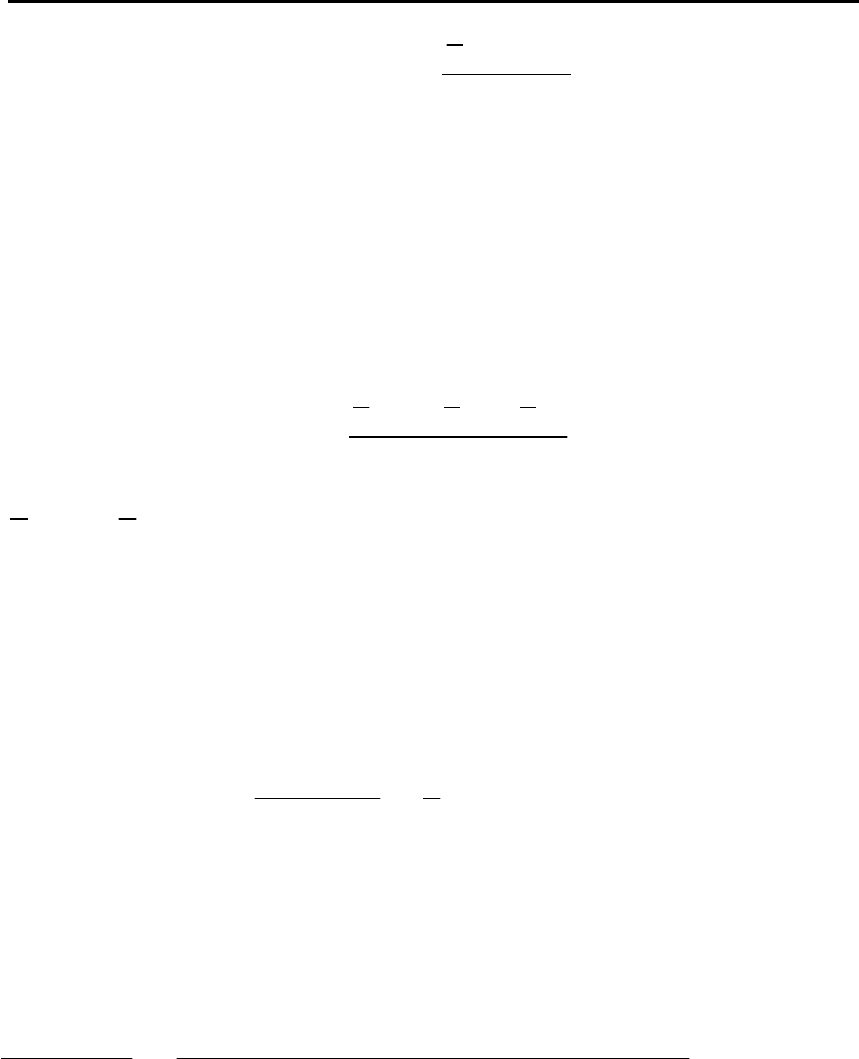
108
11
11
1
1
2
jj
j
jj
ii
ii i
yy
yy
h
τ
ϕ
++
+−
−
⎛⎞
−
=+Ψ +
⎜⎟
⎝⎠
. (2.78.б)
Для повышения порядка аппроксимации можно также ис-
пользовать более простые соотношения для разностных схем ти-
па «предиктор-корректор». После применения к обеим частям
(2.78.а) обратного оператора и преобразований можно сформиро-
вать
разностную схему «предиктор-корректор» второго типа:
111
11
11
1
2
2
()
jjj
jj j
iii
ii i
yyy
yy
h
τ
ϕ
+++
+−
−+
−+
=+Φ +
, (2.78.в)
где
1
j
j
ii
y и
y
+
вычисляются с применением явной схемы (2.76).
При
50,σ =
из (2.77) следует частично-неявный аналог
«шеститочечной» симметричной
разностной схемы типа Кран-
ка-Никольсона
для рассматриваемого кусочно-линейного одно-
мерного уравнения:
j
i
φ
j
i
y
j
i
y
τ
j
i
y
j
i
y
+
⎟
⎠
⎞
⎜
⎝
⎛
+
+
=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
+
1
2
1
1
ΛΦ
. (2.79)
Разностная схема (2.79) с учетом структуры оператора правой
части может быть преобразована к виду:
j
i
φ
h
j
i
y
j
i
y
j
i
y
j
i
y
j
i
y
j
i
y
τ
j
i
y
j
i
y
+
+
+−
−
+
+
+
+
+
−
+
−
=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
+
2
2
1
2
1
1
1
1
2
1
1
1
Φ
. (2.80)
Если в числителе дроби правой части уравнений добавить и
вычесть
4
j
i
y , ввести кусочно-линейный оператор
1
Ψ
, то (2.80)
представляется в виде, позволяющем сформировать канониче-
скую форму оператора правой части. В результате можно полу-
чить равенство:
