Козлов В.Н., Куприянов В.Е., Шашихин В.Н. Управление энергетическими системами. Часть1. Теория автоматического управления
Подождите немного. Документ загружается.

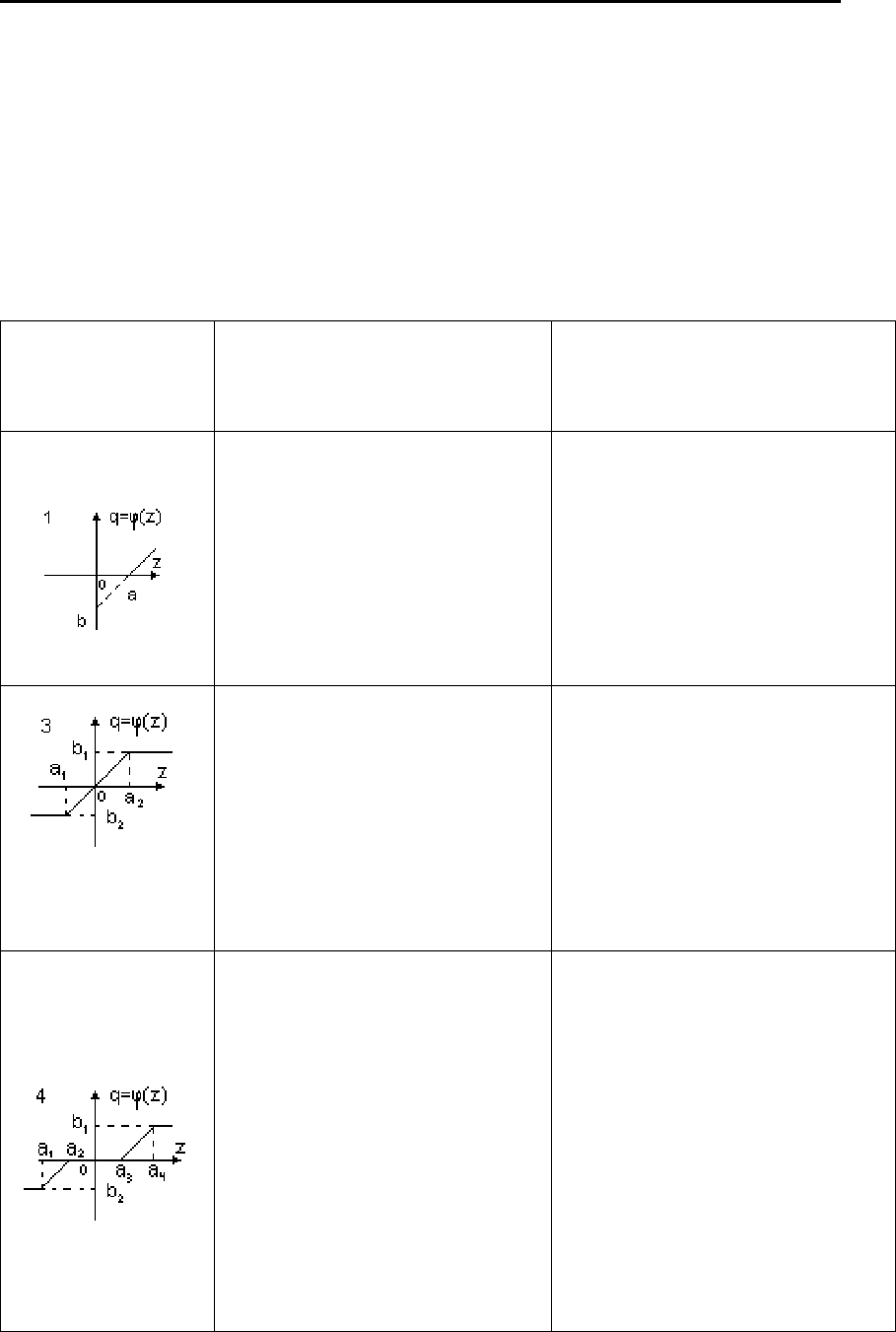
2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
89
Важные следствия и обобщения (2.59), данные в табл. 2.3,
определяют статические и динамические типовые нелинейные
звенья, включая «звенья с памятью». К последним нелинейным
звеньям относятся звенья типа «гистерезис», «люфт», которые
описываются интегро-алгебраическими или эквивалентными
Таблица 2.3
Характери-
стика нели-
нейного звена
Предикатное
описание
нелинейного звена
Описание звена
нелинейным
оператором
⎩
⎨
⎧
>−
<
=
azazk
az
),(
,0
ϕ
0,0,/
<
>−= baab
k
2/|)|
()(
az
a
z
k
z
q
−+
+
−=
=
ϕ
⎪
⎩
⎪
⎨
⎧
>
≤≤
<
=
21
21
12
,
,
,
azb
azakz
azb
ϕ
)/()(
1221
aabbk
−
−
=
2/)||
|(|)(
212
12
aaaz
azkbzq
+−−−
−
−+
=
=
ϕ
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
>
≤≤−
<<
≤≤−
<
=
41
433
32
212
12
,
),(
,0
),(
,
azb
azaazk
aza
azaazk
azb
ϕ
)/(
)/(
341
122
aab
aabk
−=
=
−
=
2/)
||
||||
|(|)(
4
3214
32
12
a
aaaaz
azaz
azkbzq
+
+−+−−−
−−+−−
−
−+
=
=
ϕ
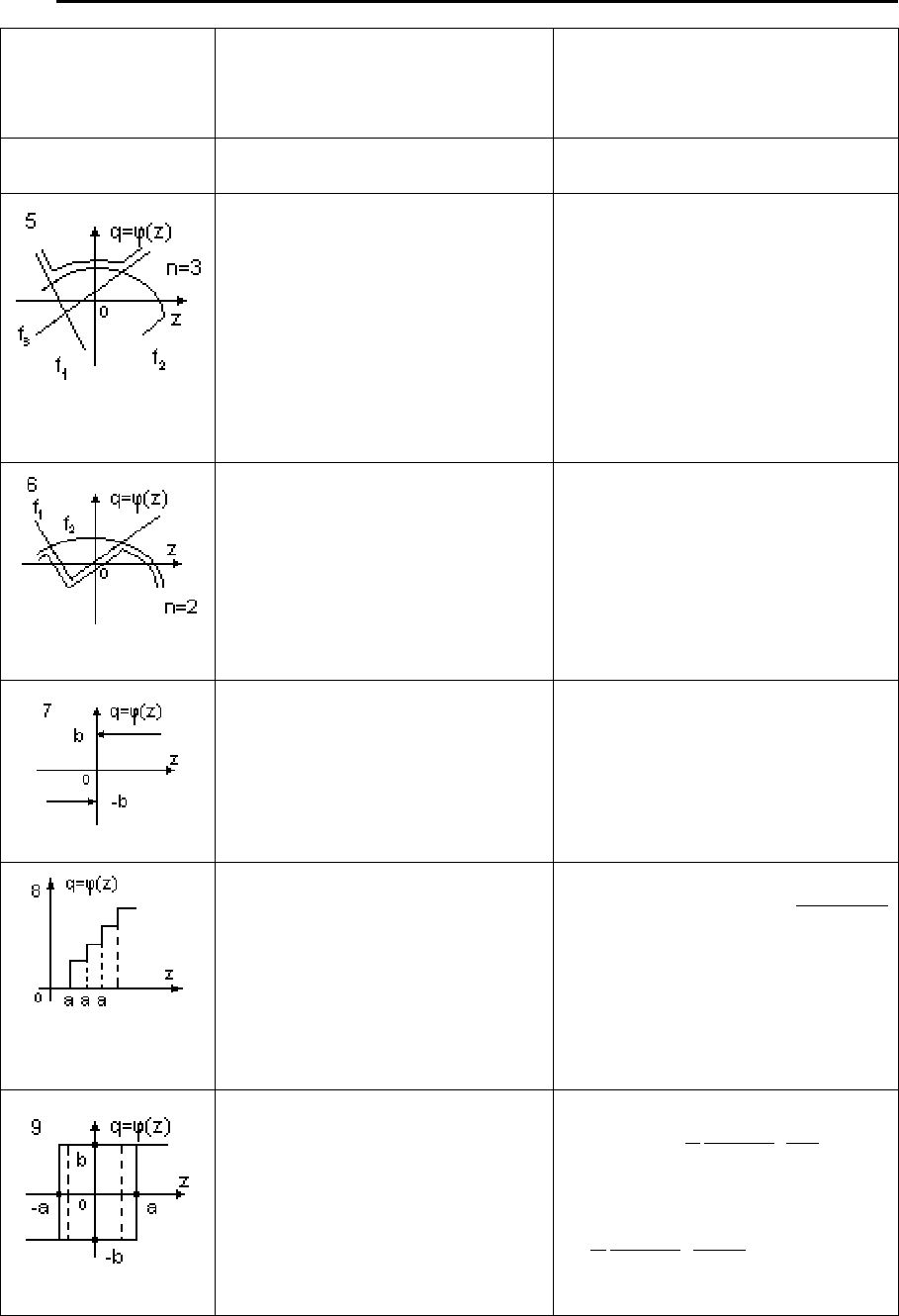
90
Характери-
стика нели-
нейного звена
Предикатное
описание
нелинейного звена
Описание звена
нелинейным
оператором
i
i
nizf ,...,2,1)),(max(
=
=
ϕ
ni
zfm
mzf
mzfzq
i
i
,...,2
)),)((max
2/|))(|
))(()(
1
1
=
=
−+
+
+=
=
ϕ
nizf
i
i
,...,2,1)),((min
=
=
ϕ
ni
zfm
mzf
mzfzq
i
i
,...,2
)),((min
,2/|))(|
)(()(
1
1
=
=
−−
−
+=
=
ϕ
⎩
⎨
⎧
<−
>
=
0,
0,
zb
zb
ϕ
=
=
=
)/|(|)(
z
z
b
z
q
ϕ
b
=
)(z
s
i
g
n
PP
P
P
aza
hb
<<
+=
−
∑
1
0
,
ϕ
slaa
az
az
hbzq
Sl
r
P
P
P
P
>>
−
−
+==
∑
=
,
,
||
)(
1
0
ϕ
Сложное
описание
)1
||
(
||
2
)1
||
(
||
2
)(
+
−
+
+
+
++
−
−
==
•
•
•
•
z
z
az
azb
z
z
az
azb
zq
ϕ
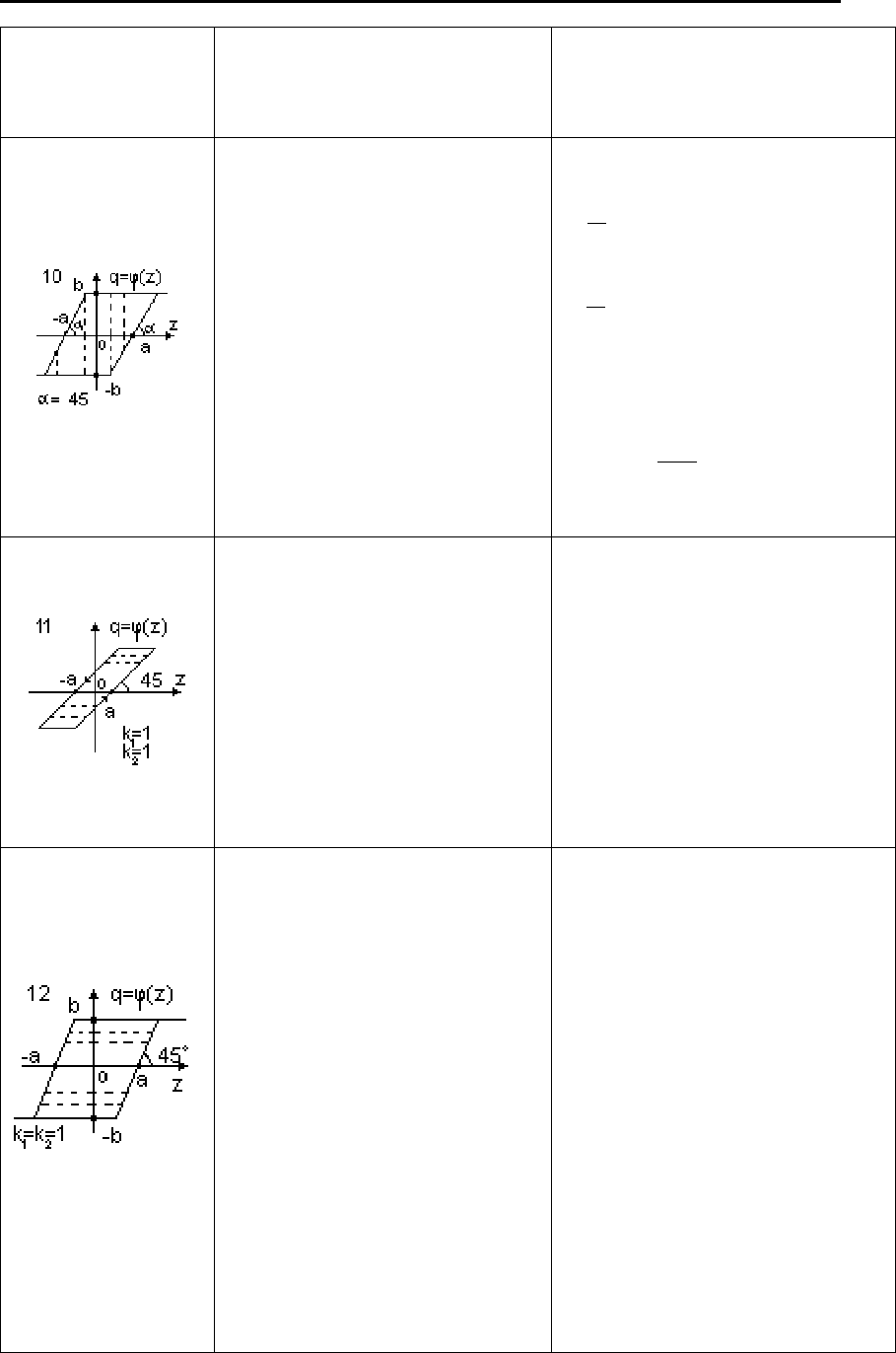
2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
91
Характери-
стика нели-
нейного звена
Предикатное
описание
нелинейного звена
Описание звена
нелинейным
оператором
Сложное
описание
2/)1
||
(
,,
,|)||(|
2
1
|)||(|
2
1
)(
+±=
+=−=
−−++
+−−+=
=
=
•
•
±
−
+
z
z
s
azazu
sbb
sbubu
z
q
ω
ωω
ϕ
Сложное
описание
1
,2/|)||(|
)(,)](
)([)0()(
|1
2
1
0
1
>>
+−−+=
=−
−+=
∫
М
azazz
zdqk
zkМqtq
t
ϕττ
τϕ
Сложное
описание
1
,2/|)||(|
)(
,2/|)||(|
)(
,)]()([
)0()()),(()(
2
1
0
21
1
2
>>
−−+=
=
+−−+=
=
−
+
+==
∫
М
bpbp
p
aqaqq
q
dzkpkМ
ptptptq
t
ϕ
ϕ
τττϕ
ϕ

92
дифференциально-алгебраическими операторами (операторы 11,
12, табл. 2.3). Приведенные описания звеньев позволяют сформу-
лировать модели объектов и систем с типовыми нелинейностями.
2.9.2. Кусочно-линейные дифференциальные и разност-
ные уравнения объектов и систем управления.
Канонические
формы
кусочно-линейных дифференциальных систем, учиты-
вающих типовые звенья, можно сформулировать различным об-
разом. Одна из таких канонических форм имеет вид:
),()(,)0(),()(
0
uDxCyxxuBxAx Ψ+Ψ==Φ+Φ=
(2.60.а)
где
mn
RuRx ∈∈ , – векторы состояний и управления;
l
Ry ∈ –
вектор выходных координат;
,
nn
RA
×
∈ ,
mn
RB
×
∈
nl
RC
×
∈ и
ml
RD
×
∈ – матрицы параметров. Координатные функции уравне-
ний (2.60.а) определяются равенствами:
Tm
m
j
j
Tn
n
i
i
uuuu
xxxx
))(,...),(,...),(()(
,))(,...),(,...),(()(
1
1
1
1
ϕϕϕ
ϕϕϕ
=Φ
=Φ
и формируются с помощью операторов (2.59) и операторами
табл. 2.3. Форма (2.60.а) включает системы с интегральными опе-
раторами, которые представлены в дифференциальной форме.
Кусочно-линейные разностные уравнения объектов и сис-
тем формулируются следующим образом:
)()(,),()(
0
01
tttttt
uDxCyxxuBxAx Ψ+Ψ==Φ+Φ=
+
. (2.60.б)
Уравнения (2.60.а) и (2.60.б) включают уравнения в форме
А. И. Лурье (когда первый оператор в системах – тождествен-
ный), используемые в задачах абсолютной устойчивости:

2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
93
.),(, xcBAxx
T
==+=
σσϕξξ
(2.61.а)
Соответствующие системе (2.61.а) кусочно-линейные разно-
стные уравнения для дискретных объектов или систем имеют
следующий вид:
,),(,
1 t
T
tttttt
xcBAxx ==+=
+
σσϕξξ
(2.61.б)
где нелинейные функции
)(
σ
ϕ
удовлетворяют «секторным усло-
виям:»
2
)(0
σσϕσ
k≤≤ . Эти условия характеризуют широкие
классы нелинейностей – звенья, описываемые операторами типо-
вых нелинейностей, разрывные и гладкие статические характери-
стики нелинейности, принадлежащие «сектору (0, k)». Пример
статических
«секторных нелинейностей» приведен на рис.2.9.
Секторные условия описывают широкий класс нелинейностей
гладкого и негладкого типа.
Рис. 2.9. К характеристике «секторных нелинейностей»
Рассмотренные кусочно-линейные дифференциальные и
разностные уравнения не охватывают общие классы моделей не-
линейных объектов и систем управления. Поэтому на практике
используются конкретизации моделей, адекватные исследуемым
y = kσ
ξ
ξ=φ(σ)
σ
0

94
объектам и системам.
2.9.3. Обобщенные модели объектов и систем управления.
С помощью введенных выше операторов можно обобщить ис-
ходные нелинейные дифференциальные уравнения объектов и
систем (без учета типовых нелинейностей)
),(),,( u
x
yu
x
f
x
Ψ
=
=
, (2.62)
где )(),( ⋅Ψ⋅
f
– вектор-функции аргументов x и u, соответствую-
щих координатам состояния и управления. Из теории дифферен-
циальных уравнений известно, что решение системы (2.62) суще-
ствует и единственно, если правые части удовлетворяют услови-
ям непрерывности и условию Липшица.
Определение 2.9.2. Обобщенные нелинейные уравнения,
учитывающие наличие нелинейных звеньев, имеют вид:
))(),(()),(),(( u
x
y
u
x
f
x
Φ
Φ
Ψ
=
Φ
Φ=
, (2.63)
где осуществлена суперпозиция координат правой части и опера-
торов типовых нелинейностей (см. табл. 2.3).
Определение 2.9.3. Условием Липшица для правой части
системы (2.63) называется условие
xxLLxfxf
f
′′
−
′
≤
⋅
′
′
Φ
−⋅
′
Φ
Φ
)),(()),(( ,
где
f
L и
Φ
L – константы Липшица для функций )(⋅
f
и )(
⋅
Φ
.
Условие Липшица представляет собой условие типа непрерывно-
сти, и позволяет оценить норму разности образов с помощью
нормы разности прообразов. При этом
«постоянная Липшица»
является параметром такой широко используемой оценки.
Утверждение 2.9.1. Если операторы и правые части диффе-
ренциальной системы (2.63) непрерывны и удовлетворяют усло-
виям Липшица, то ее
решение существует и единственно. По-

2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
95
следний факт изучен в теории дифференциальных уравнений.
Аналогично формируется пара уравнений для дискретных
объектов или систем управления. При этом уравнения без учета
операторов типовых нелинейностей записывают как
),(),,(
1 tttttt
uxyuxfx
Ψ
=
=
+
, (2.64)
а аналоги непрерывных уравнений (2.63) принимают вид
))(),(()),(),((
1 tttttt
uxyuxfx
Φ
Φ
Ψ
=
Φ
Φ
=
+
. (2.65)
Введенные модели позволяют существенно расширить воз-
можности конструктивного описания нелинейных объектов и
систем управления. Однако при этом весьма актуальной является
классическая задача о
погрешности аппроксимации нелиней-
ных уравнений кусочно-линейными уравнениями, решения кото-
рой доставляет
обобщенная теорема сравнений решений по
норме
. Эта теорема дает ответ на ряд практических вопросов,
возникающих при описании объектов и систем, на основе мето-
дов функционального анализа.
2.9.3. Численные методы анализа переходных процессов
в кусочно-линейных системах.
Рассмотрим методы анализа пе-
реходных процессов на основе разностных схем, для которых
анализируются условия устойчивости, приведенные в теоремах.
Теорема 2.9.1. Пусть выполнены следующие условия:
1. Задача Коши для кусочно-линейной системы имеет вид:
0
1
(), (0) , 1,,
n
ji i
iijij
j
x
ax x xin
ϕ
=
===
∑
где
0)0(,)(,)( =≤=
ij
j
ij
j
ij
ii
ii
xLxxx
ϕϕϕ
. Исследуется ус-
тойчивость решения
0)(
=
t
x
.

96
2. Разностная схема для решения задачи Коши (анализа пе-
реходных процессов в кусочно-линейной системе) представляет-
ся разностными уравнениями:
nihaxahxx
ii
n
ij
j
kijij
i
k
i
k
,1,)1()(
1
1
=−
⎥
⎦
⎤
⎢
⎣
⎡
+=
−
≠
+
∑
ϕ
.
Тогда решение 0
*
=
i
x разностной схемы устойчиво при условиии:
. (2.66)
Таким образом, при определенных ограничениях на пара-
метры разностная схема устойчива для любого шага
h
. В некото-
рых исследованиях аналогичные условия называются
условиями
«сверхустойчивости»
. Имеются другие способы построения раз-
ностных схем, обладающих свойством условной устойчивости
при любом шаге. Ниже рассматриваются такие разностные схемы
решения задачи Коши для кусочно-линейных систем и условия
их устойчивости, которые используется для анализа процессов.
Рассмотренные разностные схемы могут быть обобщены для ана-
лиза процессов при ненулевых входных воздействиях.
Теорема 2.9.2. Пусть выполнены следующие условия:
1.
Задача Коши для кусочно-линейной системы имеет вид
0
1
(), (0) , 1,,
n
ji i
iijij
j
x
ax x xin
ϕ
=
===
∑
где
ii
ii
xx =)(
ϕ
, причем
j
ij
j
ijii
xLx ≤= )(,0)0(
ϕϕ
. Исследуется ус-
тойчивость решения
0)(
=
t
x
.
2.
Разностная схема для исследуемой кусочно-линейной
дифференциальной системы представлена системой алгебраиче-
ских равенств
∑
≠
=
>><
n
ij
j
ijijiiii
hLaaa
1
0,,0

2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
9
7
∑
=
+
===
n
j
jj
k
j
kijij
i
k
nixxxHx
1
001
,,1,),(
ϕ
где параметры разностной схемы определяются следующими ра-
венствами:
,(1)/.
ii
ah
ii ij ii ij ii
He H H aa==−
Тогда условия устойчивости решения
0
=
∗
x
имеют вид:
(2.67)
Как видно из утверждений последних теорем, условия ус-
тойчивости для постоянной Липшица
1
ij
L
=
включают условия
типа Адамара для матриц исходной кусочно-линейной системы.
Рассмотрим устойчивость обобщенных разностных схем.
Теорема 2.9.3. Пусть выполнены следующие условия:
1.
Задача Коши для кусочно-линейных объектов пред-
ставлена соотношениями для кусочно-линейных уравнений:
0
)0(),()( xxuBФxAФx
ux
=
+
=
.
2. Разностная схема для задачи Коши имеет вид:
[
]
huФxФxx
kkkk
),(),(,
1
Ψ=
+
,
где
[]
)()(()(
2
1
1
kkk
uhBФxФhAxA ++=•Ψ
−
−
−
Φ
, причем
[
]
•
−1
Ф
-
оператор, обратный для кусочно-линейного оператора
)(
•
Ф
,
координатные функции которого определены функциями –
i
ϕ
, а
стационарная точка
∗
x
разностной схемы единственна и опреде-
ляется при условии:
),0[,
*
∞
∈
=
= kconstuu
k
, системой кусочно-
линейных алгебраических уравнений
[
]
[]
*
1
**2*
11
*
)()(( zФuhBФxФhAxAФx
ux
−−−
=
+
+=
,
.0,,0
1
∑
=
>><
n
j
ijijiiii
hLaaa
98
причем операторы системы и разностной схемы липшицевы:
.][][,][][
'''
2
''''''
1
''1'1
yyLyФyФzzLzФzФ
xx
−≤−−≤−
−−
Тогда стационарная точка схемы
*
x устойчива, если выполнены
условия:
()
22
1
1
1
1
0
LA
AL
h
−
<<
−
−
,
.1||||
1
1
<
−
AL
(2.68)
Доказательство. Рассмотрим цепочку соотношений для
норм элементов
x
конечномерного пространства
n
R
, в котором
норма определена равенством
1,...,
|| || max | |
i
in
xx
=
=
. Тогда можно полу-
чить совокупность оценок норм отклонений решений от стацио-
нарного значания:
[]
[]
.1(
)()(
)(()((
][][
*22
1
1
*2*
1
1
*2*
1
2
1
1
*1*
11
*1
xxLAhAL
xФxФhAxxAL
xФhAxAxФhAxAL
zzLzФzФxx
k
xkxk
xkxk
kkk
−⋅+⋅≤
≤−+−⋅≤
≤+−+=
=−≤−≤−
−
−
−−
−−
+
Воспользовавшись принципом сжимающих отображений,
можно записать условие сжатия для оператора разностной схемы:
1)1(
22
1
1
<+
−
LAhAL
. Разрешая последнее условие относительно
h, получаем утверждение теоремы.
Рассмотренные разностные схемы порождают соответст-
