Козлов В.Н., Куприянов В.Е., Шашихин В.Н. Управление энергетическими системами. Часть1. Теория автоматического управления

Подождите немного. Документ загружается.

3. МЕТОДЫ АНАЛИЗА УСТОЙЧИВОСТИ ОБЪЕКТОВ И СИСТЕМ УПРАВЛЕНИЯ

129

Тогда, чтобы стандартный полином (3.11) был гурвицевым, необ-

ходимо и достаточно, чтобы выполнялось условие неотрицатель-

ности диагональных миноров:

,1,0 =>Δ .

Доказательство. В основе доказательства – индукция по

степени полинома (3.11).

База индукции: пусть n = 1, тогда

101

)( aa +=

, а вещественный корень 0/

011

−

, так как

>aa .

Индукционный переход: пусть k=n и условия Гурвица вы-

полнены для

)(

. Покажем, что условия Гурвица будут вы-

полнены и для полинома

)(

Q степени (n+1). Рассмотрим

)(

в соответствии с (3.12)

02)],()()[(

)(

>=++=

γλχλλχλλ

ccQ

nnn

и определим связь коэффициентов )(

Q и )(

. Если рас-

смотреть два полинома

...)(

,...)(

−

+++=

++++=

AAAQ

aaaa

λλλ

λλλλχ

то в силу вида )(

Q можно получить

[]

.))1(...()...)((

...

nnn

aaaaaac

AAA

−++−+++++=

=+++

−−

λλλλλλ

λλ

Приравняем коэффициенты правой и левой частей при сте-

пенях

, учитывая, что с = 2γ. Тогда можно получить следующее

130

семейство равенств для коэффициентов при совпадающих степе-

нях:

;

0000

aaaA

=+=

;)(

01101

aaaacA

γλ

=−+=

212212

:( ) ;

ca a a a a

λγ

−

=++=+

γλ

−

434

aaA

−

γλ

. . . . .

21222212 kkkkk

aaAaA

−−−

Главный диагональный минор порядка (k+1) матрицы Гурвица

полинома

)(

Q можно представить в силу приведенных ниже

равенств:

222122

2434

0212

112212

345

123

kkkk

aaaa

AAAA

AAA

Δ=

−−

+−+

γγγ











3. МЕТОДЫ АНАЛИЗА УСТОЙЧИВОСТИ ОБЪЕКТОВ И СИСТЕМ УПРАВЛЕНИЯ

131

Здесь

, kk – число нечетных и четных столбцов;

– главный

минор k-го порядка матрицы Гурвица. Необходимость доказана.

Часто параметры объектов и систем управления не могут

быть определены точно. В такой ситуации возникает задача ана-

лиза соответствующих корней семейства полиномов, удовлетво-

ряющих

интервальным ограничениям на коэффициенты по-

линомов.

В теории автоматического управления важное место зани-

мают

критерии интервальной устойчивости, под которыми

понимают асимптотическую устойчивость при условии, когда

параметры коэффициентов характеристического полинома объ-

екта (системы) управления неизменны и принадлежат некоторым

областям. Если коэффициенты характеристических полиномов

принадлежат заданным интервалам, то критерий интервальной

устойчивости сформулирован В.Л. Харитоновым (1978 г.). Кри-

терий может использоваться для синтеза адаптивных систем

управления в интервальной постановке.

Критерий интервальной устойч

ивости является достаточно

важным в современной теории и практике управления. Интер-

вальная модель для описания параметров объекта или системы

управления, используемая в критерии, позволяет решить ряд

важных задач управления. К ним относятся задачи теории грубых

(робастных) систем и изучаемых в теории адаптивного управле-

ния, поскольку в данной модели конструктивно определен класс

адаптац

ии.

Теорема 3.4.3 (критерий интервальной устойчивости

В.Л. Харитонова

). Пусть задано семейство алгебраических по-

линомов с вещественными интервальными коэффициентами,

удовлетворяющих условиям:

{

}

.,0,)( nkaaaF

=≤≤=

λχχ

132

Семейство полиномов устойчиво тогда и только тогда, ко-

гда все корни полиномов

)(),(),(

321

fff и )(

f имеют от-

рицательные вещественные части. При этом полиномы

4,1)( =if

имеют следующие коэффициенты:

⎪

⎩

⎪

⎨

⎧

−

⎪

⎩

⎪

⎨

⎧

−

⎪

⎩

⎪

⎨

⎧

−

⎪

⎩

⎪

⎨

⎧

−

⎪

⎩

⎪

⎨

⎧

−

⎪

⎩

⎪

⎨

⎧

−

⎪

⎩

⎪

⎨

⎧

−

⎪

⎩

⎪

⎨

⎧

−

−−

−

−−

−

−−

−

−−

−

.нечетно,

четно,,

нечетно;,

четно,,

:)(

нечетно;,

четно,,

нечетно;,

четно,,

:)(

нечетно;,

четно,,

нечетно;,

четно,,

:)(

нечетно;,

четно,,

нечетно;,

четно,,

:)(

Теорема позволяет анализировать устойчивость непрерыв-

ных объектов или систем с учетом интервальных ограничений на

параметры, что является весьма важным при проектировании

систем управления при отсутствии полной информации о пара-

метрах. Задание интервалов изменения коэффициентов характе-

ристического полинома характеризует степень неопределенности

объекта (системы).

3.4.2. Критерии устойчивости дискретных объектов и

систем управления.

Модели объектов (систем) для анализа ус-

тойчивости в дискретном времени могут быть представлены

уравнениями «вход–выход» или уравнениями «вход-состояния-

выход». Эти модели подробно изучены в разделе 2 и имеют сле-

дующий вид:

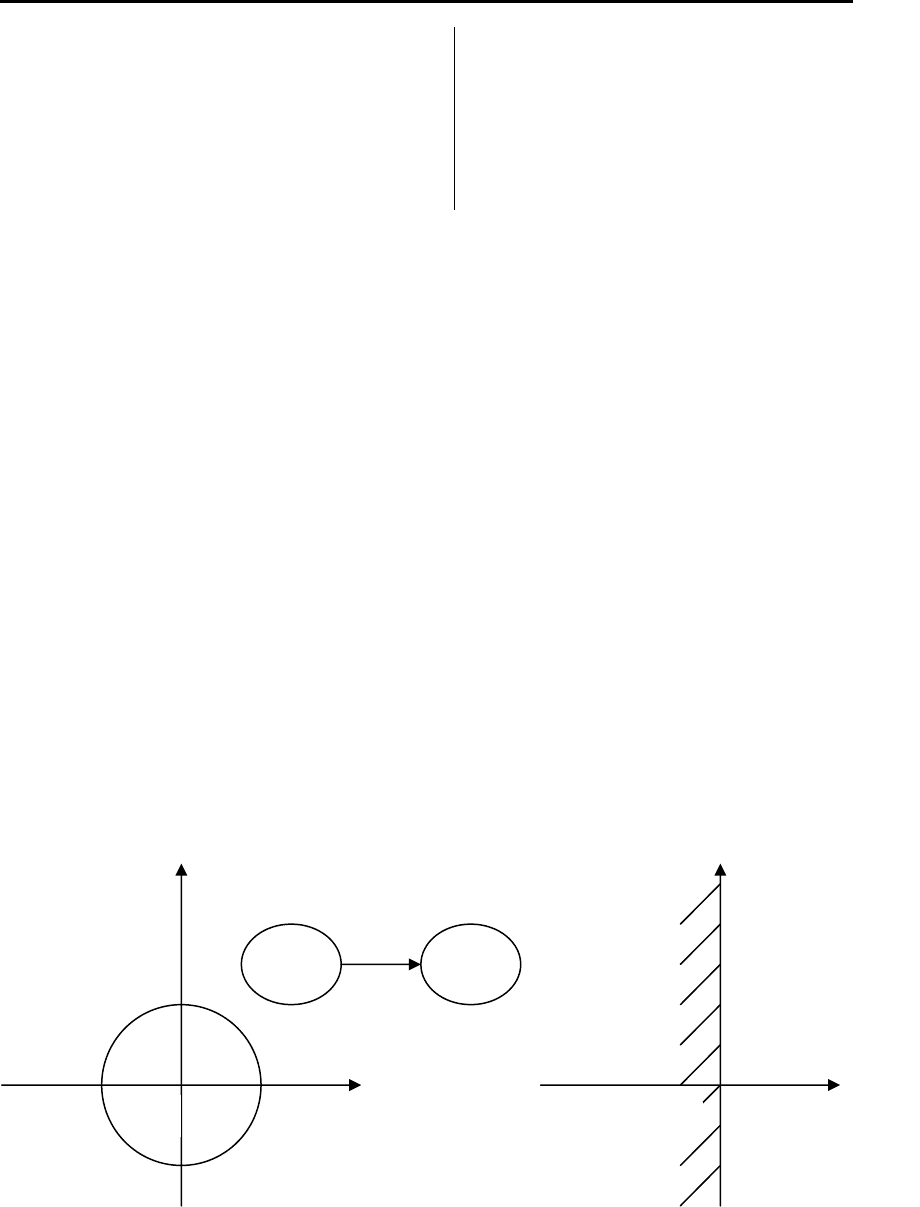
3. МЕТОДЫ АНАЛИЗА УСТОЙЧИВОСТИ ОБЪЕКТОВ И СИСТЕМ УПРАВЛЕНИЯ

133

,)())((

,)()(

uBAy

uByA

ξξ

−

ttt

uDxCy

uBxAx

)(

uDBA

ECy

⎥

⎦

⎤

⎢

⎣

⎡

−

−=

Пусть характеристический полином модели имеет вид

bbbb ++++=

−

λλλλχ

...)( . (3.13)

Для исследования устойчивости дискретных систем требу-

ется определить расположение корней

)(

относительно ок-

ружности единичного радиуса (см. п. 3.3).

Рассмотрим условия принадлежности корней полинома ок-

ружности единичного радиуса, решив задачу с помощью крите-

рия Гурвица. Для этого выполним замену переменных в (3.13) по

формуле

)1/()1( ww −

или )1/()1(

−

w , что соответству-

ет преобразованию единичного круга в левую полуплоскость, ил-

люстрируемому графически на рис. 3.3. В результате полином

)(

преобразуется к виду:

Рис. 3.3. Иллюстрация преобразования единичного круга в

полуплоскость для исследования устойчивости

Im λ

Im w

Re w

134

)1(

)(

...

)(

−

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

где

awawawD +++=

−

...)(

101

. Для анализа устойчивости

)(

wD можно использовать критерий Гурвица.

Рассмотрим другой способ анализа устойчивости.

Теорема 3. 4.4 (критерий Шура – Кона). Полином

aaaa ++++=

−

λλλλχ

...)(

имеет корни

, если знаки определителей

строго чере-

дуются:

0>Δ

при четном k и 0

при нечетном k. При этом

Δ - определитель порядка 2k, формируемый из подматриц:

(

)

()

=Δ

где подматрицы определяются равенствами:

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

−−+−+−

−−

−

021

aaa

nknkn











Пример 3.4.1. Пусть задан характеристический полином

дискретной системы:

05.04.0)(

−+=

λλλχ

. Исследуем устой-

чивость системы, не вычисляя корней полинома. Используя ко-

эффициенты полинома

05.0,4.0,1

210

−

aaa , вычислим оп-

ределители:

3. МЕТОДЫ АНАЛИЗА УСТОЙЧИВОСТИ ОБЪЕКТОВ И СИСТЕМ УПРАВЛЕНИЯ

135

для k=1:

,1,05.0

=−= AA 0105.0

05.01

105.0

<−=

−

=Δ ;

для k=2:

14.0

05.04.0

005.0

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

−

= AA

8186.0

05.0014.0

4.005.001

1005.04.0

4.01005.0

−

=Δ .

Чередование знаков определителей 0,0

>Δ

свиде-

тельствует об устойчивости системы. Действительно, для харак-

теристического полинома системы справедливо представление:

)5.0)(1.0()( +−=

Рассмотренные критерии устойчивости используются для

анализа устойчивости объектов и синтеза систем управления.

3.5. Частотные критерии Михайлова и Найквиста

Рассмотрим методы анализа устойчивости объектов (сис-

тем) управления по годографам характеристических полиномов и

амплитудно-фазовых характеристик.

3.5.1. Критерии Михайлова и Найквиста для непрерыв-

ных объектов и систем.

Пусть характеристический полином, со-

ответствующий анализируемой системе, имеет вид:

aaaa ++++=

−

λλλλχ

...)( .

Требуется найти условия устойчивости )(

с помощью

136

частотного представления годографа )(

Лемма 3.5.1 (принцип аргумента для непрерывных сис-

тем). Пусть полином

)(

имеет m корней, расположенных в

правой полуплоскости, и (n–m) корней – в левой полуплоскости.

Тогда при изменении частоты ω в пределах от –∞ до ∞

измене-

ние аргумента полинома

)(

равно разности между числа-

ми левых и правых корней, умноженной на π.

Доказательство. Полином )(

может быть разложен на

множители

∏

−=

)()(

λλλχ

где

iii

+= – корни полинома. Рассмотрим значение поли-

нома при

j= :

arg ( )

() () .

jje

χω χω

При этом будут выполнены следующие условия:

()

jaj

ωωλ

=−

∏

∑

−=

)(arg)(arg

λωωχ

Рассмотрим множитель (

−

). Его модуль не равен ну-

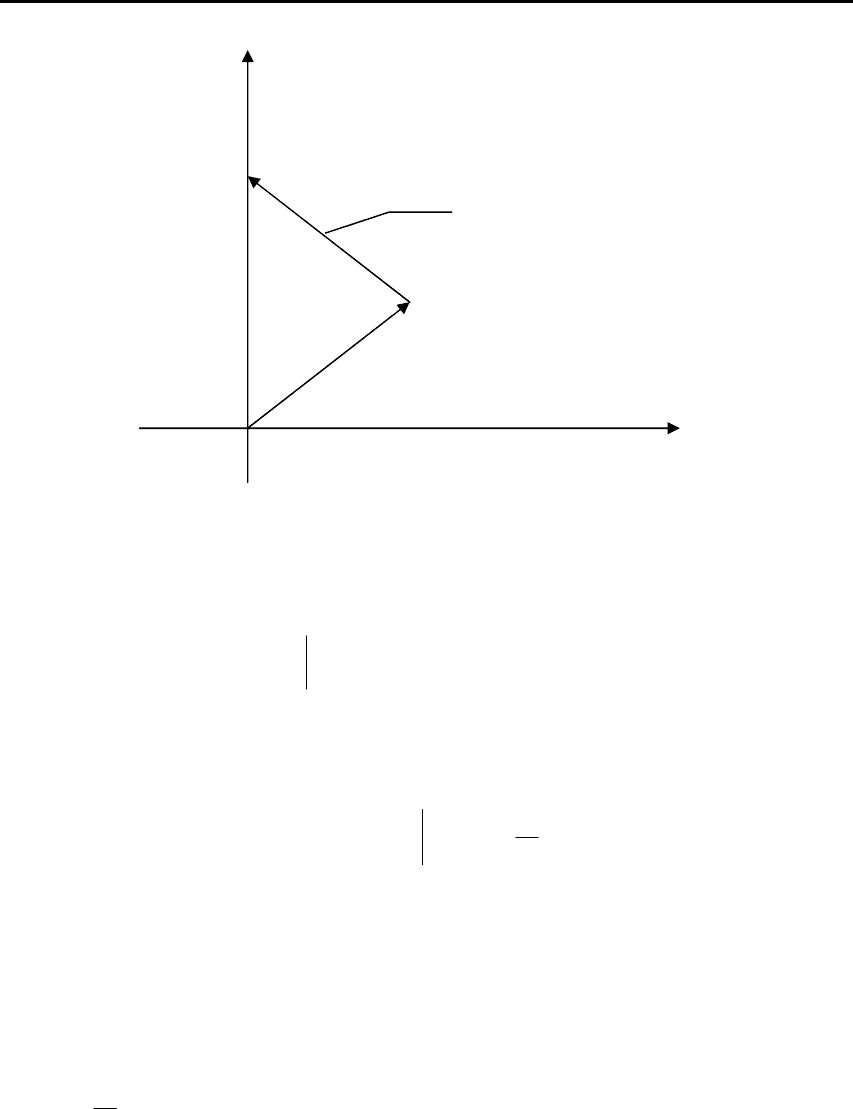
лю, если корень не расположен на мнимой оси. На рис. 3.4 пред-

ставлен вектор (

− ), соответствующий расположению корня

в правой полуплоскости. При изменении параметра ω от –∞ до ∞

аргумент изменится на угол

−

)(arg

j , если корень

расположен в правой полуплоскости, и на угол π, если в левой

полуплоскости.

Пусть

)(

имеет m правых корней и n–m левых корней.

Тогда при изменении частоты ω от –∞ до ∞ изменение аргумента

)(

равно разности между числом левых и правых корней

3. МЕТОДЫ АНАЛИЗА УСТОЙЧИВОСТИ ОБЪЕКТОВ И СИСТЕМ УПРАВЛЕНИЯ

Рис. 3.4. К иллюстрации принципа аргумента

характеристического полинома, умноженной на π :

.)2()()(arg mnmmnj

−=−−=Δ

∞=

−∞=

πππωχ

Обычно рассматривают только положительные значения

частот

),0[ ∞∈

, тогда поворот будет вдвое меньший:

.)2(

)(arg

mnj

−=Δ

∞=

ωχ

Отсюда непосредственно следует критерий Михайлова.

Утверждение 3.5.1 (критерий Михайлова). Система (объ-

ект) является устойчивой, если при возрастании ω от 0 до ∞ ком-

плексный вектор

)(

(годограф Михайлова) повернется на

угол

, где n – степень характеристического полинома

)(

Годограф

)(

при изменении ω от 0 до ∞ обходит по-

следовательно, начиная с положительной действительной полу-

оси в положительном направлении (против часовой стрелки), n

квадрантов. На рис. 3.5 приведены примеры устойчивых годо-

графов Михайлова

)(

для непрерывных объектов (систем)

iii

−

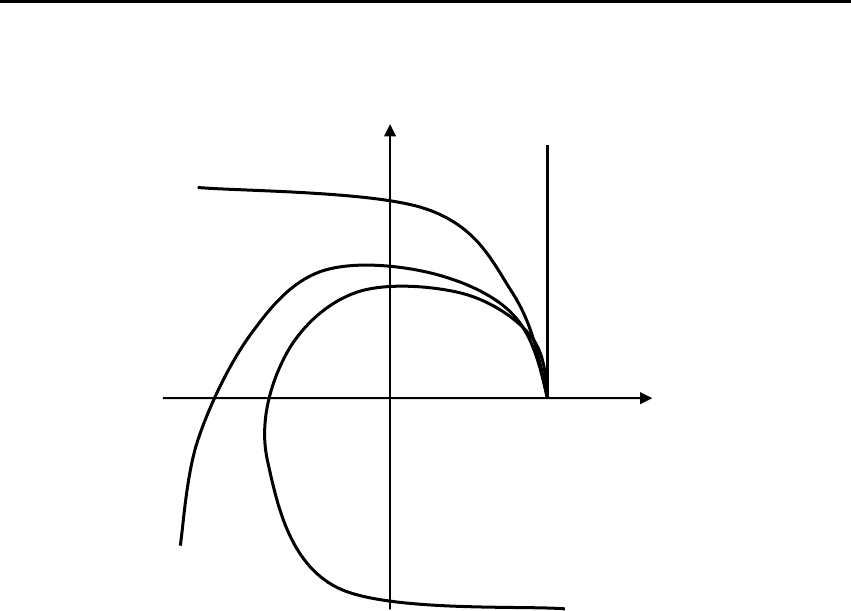
138

управления различных порядков

(

)

)()()(

jVUj

Рис. 3.5. Примеры устойчивых годографов Михайлова

Сформулируем критерий устойчивости в терминах

ампли-

тудо-фазовых частотных характеристик (АФЧХ)

объектов

или систем управления.

Утверждение 3.5.2 (критерий Найквиста). Система, ус-

тойчивая в разомкнутом состоянии, будет устойчива в замкнутом

состоянии, если АФЧХ разомкнутой системы W(s), s=jω, ω

∈

[0,∞) не охватывает точку (–1, j0) (рис. 3.6).

Если система в разомкнутом состоянии неустойчива и ее ха-

рактеристический полином имеет m корней в правой полуплоско-

сти, то для устойчивости САУ в замкнутом состоянии необходи-

мо и достаточно, чтобы АФЧХ W(jω) охватывала точку (–1, j0) в

положительном направлении m/2 раз.

На рис. 3.7 геометрически иллюстрируется эта ситуация дл

случая

4m =

n=2

n =1

n=3

n=4