Козлов В.Н., Куприянов В.Е., Шашихин В.Н. Управление энергетическими системами. Часть1. Теория автоматического управления
Подождите немного. Документ загружается.

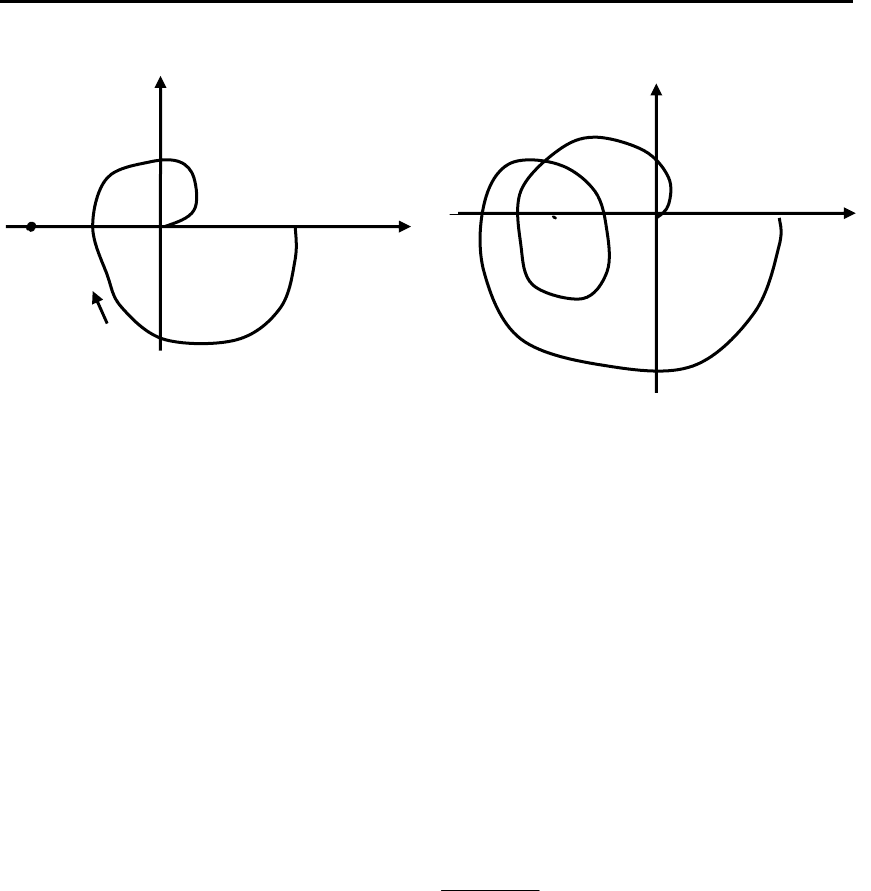
3. МЕТОДЫ АНАЛИЗА УСТОЙЧИВОСТИ ОБЪЕКТОВ И СИСТЕМ УПРАВЛЕНИЯ
139
Рис. 3.6.Годограф устойчивых Рис. 3.7. Примеры устойчивых
ОУ или САУ по критерию по критерию Найквиста ОУ
Найквиста или САУ с корнями в правой
полуплоскости
При сложной форме характеристики W(jω) могут возник-
нуть затруднения при определении числа оборотов вокруг крити-
ческой точки
)0,1(
j
− . У астатических систем, передаточные
функции которых в разомкнутом состоянии содержат интегри-
рующие звенья, АФЧХ не образует замкнутого контура:
()
(
)
()
,
P
s
Ws
s
Qs
ν
= (3.14)
где P(s), Q(s) – полиномы, не имеющие корней равных нулю, ν –
порядок астатизма. Действительно, при ω=0 характеристика
W(jω) обращается в бесконечность, а АФЧХ претерпевает разрыв.
Необходимо связать контуром значения АФЧХ при изменении ω
от –ε до +ε. При переходе частоты ω через «0» вектор jω изменя-
ет аргумент от –π при ω = –ε до +π пр
и ω = ε, причем направле-
ние изменения аргумента не определено. Чтобы освободиться от
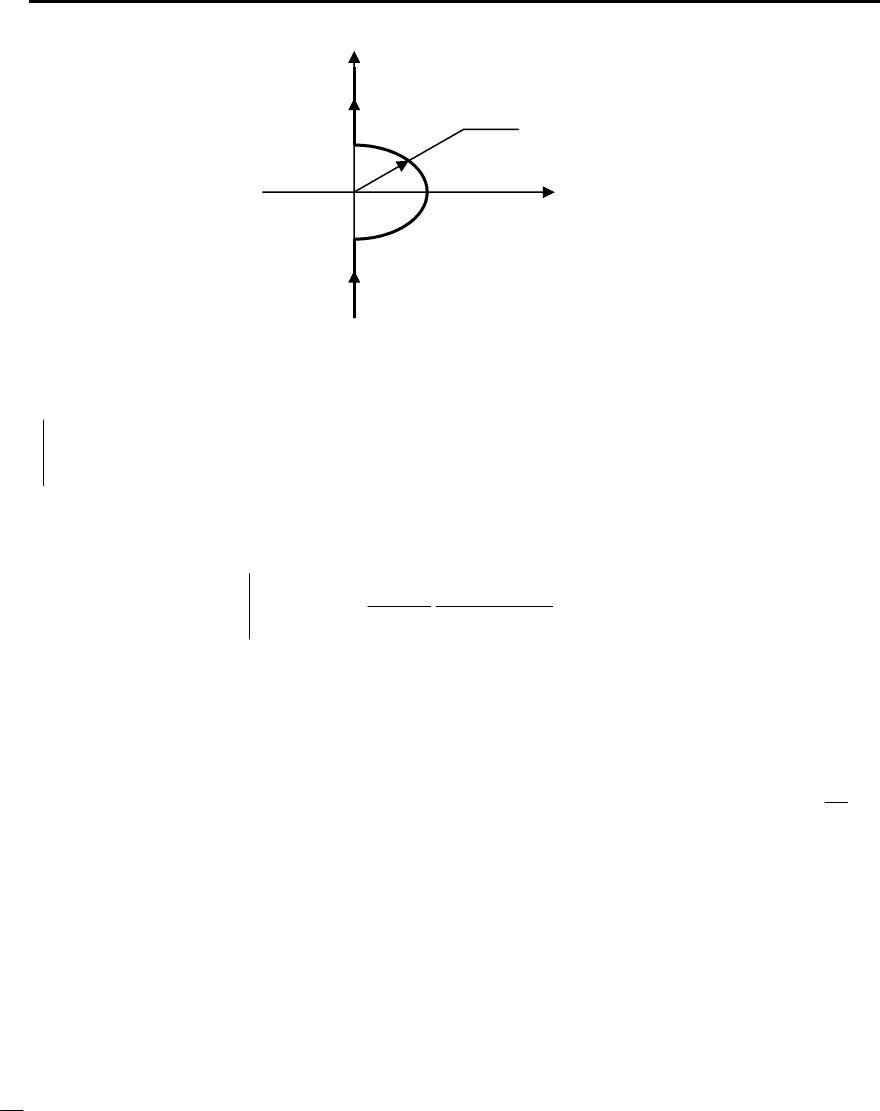
неопределенности, будем обходить начало координат в правой
полуплоскости по окружности малого радиуса r, как показано на
рис. 3.8, что отразится на поведении АФЧХ следующим образом:
-
1
ω
ω=0
0
ω→∞
Im
-1
m=4
ω→∞
ω=0
Im
Re
Re
0
140
Рис. 3.8. К устранению неопределенности
γ
j
ers
sW
=
)( , где r→0, -π/2 ≤ γ ≤ π/2, величина Δγ = +π. Тогда, учи-
тывая малую величину r и соотношение (3.14), получим
Ψ
=
=
⋅
=
j
j
ers
eR
er
Q
P
sW
j
νγ
γ
)(
1
)0(
)0(
)(
,
где R→∞ при r→0, а изменение аргумента
ν
π
γ
ν
ψ
−
=Δ−=
Δ
.
При рассмотрении только положительных частот
),0[ ∞∈
ω
изме-
нение аргумента будет определяться соотношением
ν
π
ψ
2
−=Δ .
На основании изложенного можно сделать следующий вывод.
Для определения устойчивости системы с астатизмом любого по-
рядка ν достаточно построить одну ветвь АФЧХ разомкнутой
системы, соответствующую положительным частотам, дополнить
ее дугой бесконечно большого радиуса с центральным углом
ν
π
2
− и применить рассмотренный выше критерий Найквиста.
3.5.2. Критерии Михайлова и Найквиста для дискретных
объектов и систем.
Пусть дискретные объекты (системы) опи-
сываются полиномиальной моделью «вход–выход»:
(
)
(
)
tt
aybu
ξ
ξ
=
,
r
I
m
Re
0
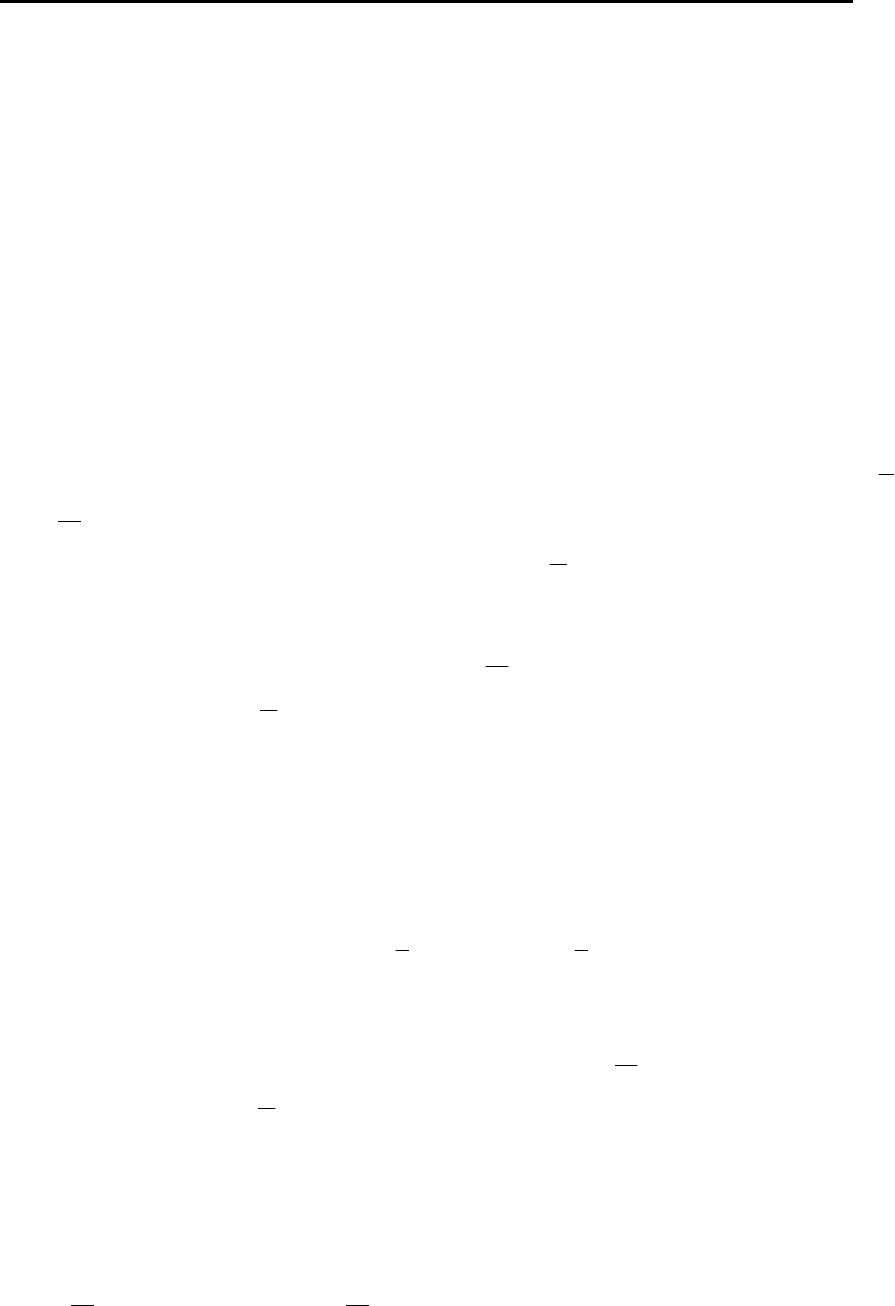
3. МЕТОДЫ АНАЛИЗА УСТОЙЧИВОСТИ ОБЪЕКТОВ И СИСТЕМ УПРАВЛЕНИЯ
141
где ξ – оператор сдвига, ,...)(
1
10
n
nn
aaaa +++=
−
ξξξ
n
nn
bbbb +++=
−
...)(
1
10
ξξξ
, или уравнениями состояний:
.,
1 tttttt
uBxCyuBxAx +=+=
+
Пусть характеристический полином системы имеет вид:
n
nn
n
aaa +++=
−
1
10
)(
λλλχ
. (3.15)
Как было показано в п. 2.6.2, для анализа частотных характери-
стик дискретных систем используется подстановка
ω
j
ez
zW
=
|)(
*
,
где
ω
– относительная частота. Годограф Михайлова может быть
получен при подстановке в (3.15)
ω
λ
j
e= .
Лемма 3.5.2 (принцип аргумента для дискретных сис-
тем
). При изменении параметра
ω
от 0 до π изменение аргу-
мента
πχ
ω
re
j
n
=Δ )(arg , где r – число корней характеристиче-
ского уравнения, лежащих внутри единичной окружности.
Доказательство. Полином )(
λ
χ
n
может быть разложен на
множители и частотная характеристика определена равенством:
() ()
0
1
n
jj
ni
i
eae
ωω
χ
λ
=
=−
∏
.
Для указанного изменения параметра
ω
справедливо соот-
ношение
πλ
ω
=−Δ )(arg
i
j
e , если выполнено условие 1||
<
i
λ
.
Если это условие не выполнено, то изменение аргумента равно
нулю. Поэтому, чтобы многочлен степени n имел все корни стро-
го внутри единичной окружности, необходимо, чтобы годограф
)(
ω
χ
j
n
при изменении
ω
от 0 до π обходил последовательно в
положительном направлении 2п квадрантов. Это утверждение –
142
критерий Михайлова. Годографы Михайлова устойчивых дис-
кретных ОУ (САУ) даны на рис. 3.9.
Рис
. 3.9. Годографы устойчивых по Михайлову ОУ (САУ)
Критерии Найквиста для дискретных и непрерывных систем
аналогичны и формулируются в виде утверждения.
Утверждение 3.5.3. Пусть передаточная функция разомкну-
той системы имеет вид:
)(
*
zW
. Чтобы замкнутая дискретная сис-
тема была асимптотически устойчива, необходимо и достаточно,
чтобы годограф
ω
j
ez
zW
=
|)(
*
при изменении
ω
от 0 до π обходил
точку (–1, j0) последовательно в положительном направлении m/2
раз, где m – число полюсов передаточной функции разомкнутой
системы
)(
*
zW , расположенных вне круга единичного радиуса
1|| >
i
z . Если разомкнутая система устойчива, то m=0. Замкнутая
система будет устойчива, если годограф
ω
j
ez
zW
=
|)(
*
не охваты-
вает точку (–1, j0) при изменении
ω
от 0 до π.
I
m
R
e
n=3
n=2
n=1
ω
0

3. МЕТОДЫ АНАЛИЗА УСТОЙЧИВОСТИ ОБЪЕКТОВ И СИСТЕМ УПРАВЛЕНИЯ
143
Сформулированные критерии позволяют исследовать ус-
тойчивость при различных исходных данных и параметрах объ-
ектов и систем управления.
3.6. Критерий абсолютной устойчивости
Абсолютная устойчивость определяется как асимптотиче-
ская устойчивость в целом, т.е. для любых начальных состояний
и для определенного класса нелинейностей из заданного сектора.
Определение 3.6.1. Пусть система (объект) управления опи-
сываются уравнениями
,)0(,),(,
0
xxxcybyAxx
T
===+=
σσϕ
(3.16)
где )(
σ
ϕ
– нелинейная функция, удовлетворяющая «секторным
условиям»
2
)(0
σσϕσ
k≤≤ . (3.17)
Абсолютной устойчивостью системы (3.16), (3.17) назы-
вается
асимптотическая устойчивость в целом (во всем про-
странстве состояний).
Теорема 3.6.1 (критерий В.М. Попова). Пусть все полюсы
передаточной функции линейной части системы
()
Ws лежат в
левой полуплоскости, а характеристики нелинейного элемента
удовлетворяют секторным условиям (3.17).
Тогда система (3.16), (3.17) абсолютно устойчива, если су-
ществует такое вещественное число q, что выполняется частотное
условие:
bAEjcjWkjWjq
n
T
1
)()(,0/1)()1(Re
−
−=>++
ωωωω
(3.18)
для всех
),0[ ∞∈
ω
и все полюсы передаточной функции линей-
ной части системы
)(
s
W
лежат в левой полуплоскости.
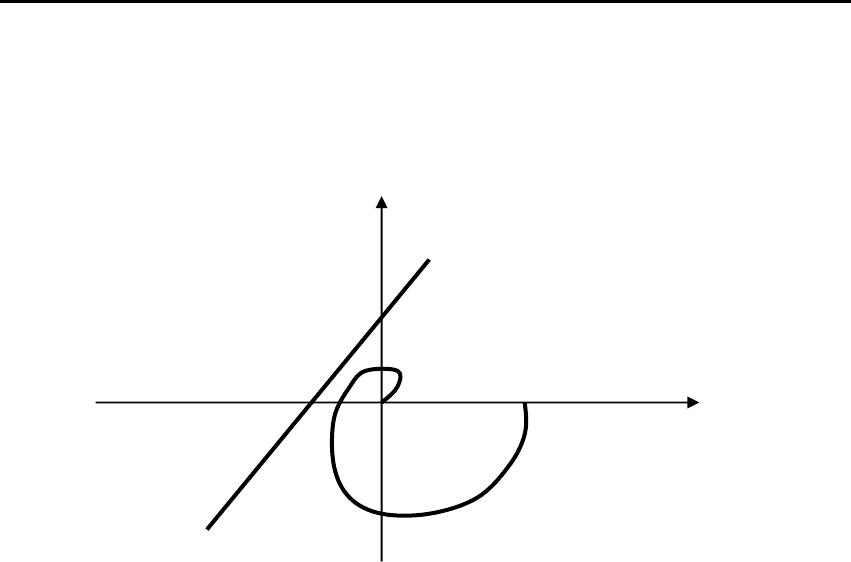
144
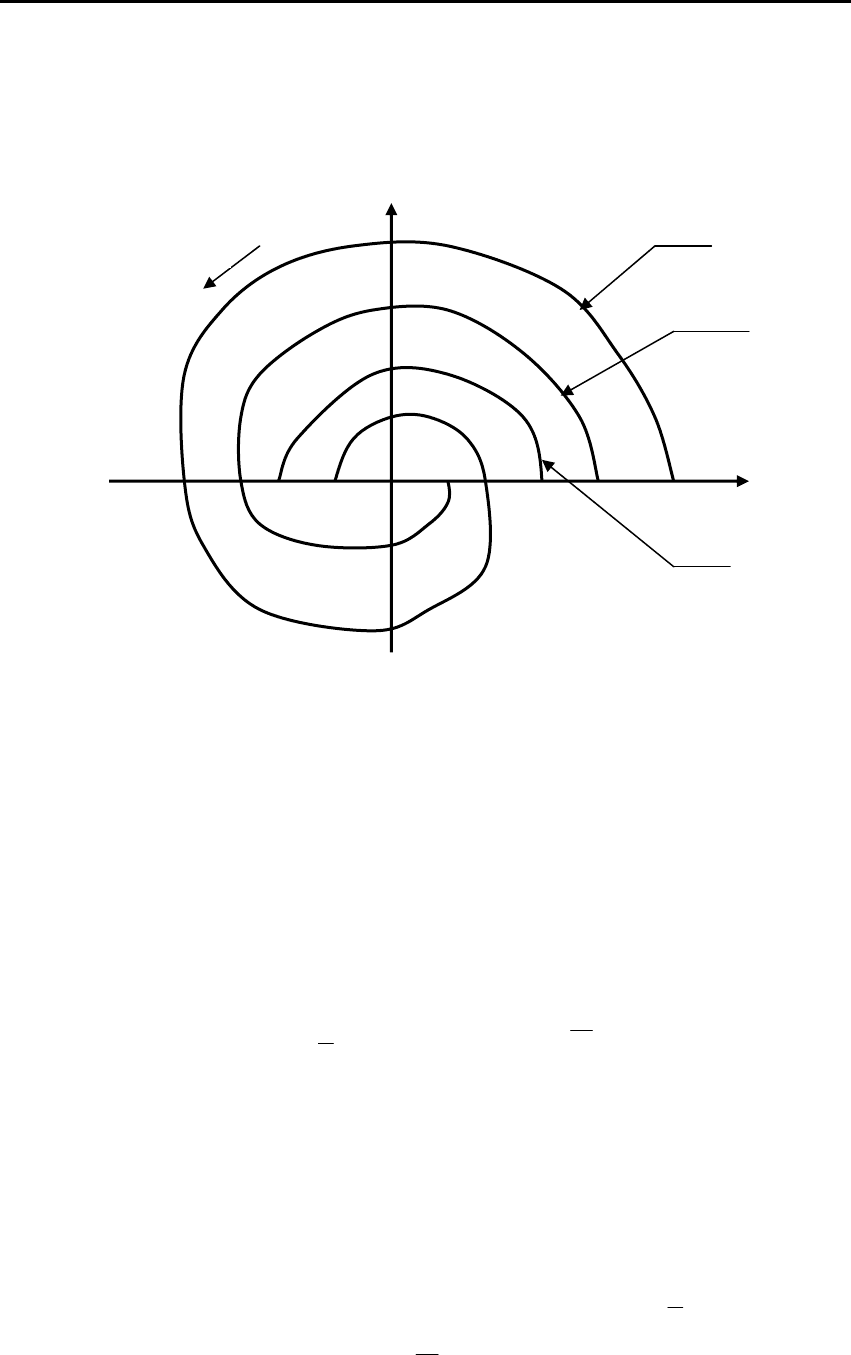
Графическая иллюстрация частотного условия представлена
на рис. 3.10. Состояние равновесия нелинейной системы абсо-
лютно устойчиво, если через точку (–1/k, j0) можно провести
Рис. 3.10. Иллюстрация частотного условия
прямую так, что она не пересечет модифицированную частотную
характеристику
)(
ω
jW
м
, которая отличается от частотной харак-
теристики линейной части масштабным множителем ω по мни-
мой оси
( ) real( ( )) imag( ( )).
M
Wj Wj j Wj
ω
ωω ω
=+
Существуют другие критерии абсолютной устойчивости,
сформулированные, в частности, в трудах В.М. Попова, В.А.
Якубовича и их учеников. Критерий абсолютной устойчивости
можно рассматривать также как «критерий грубости» для систем
с «
секторной неопределенностью» для нелинейностей, по-
скольку описывает условия устойчивости широкого класса сис-
тем с отличающимися нелинейностями.
-1/k
Im
Re
0

4. МЕТОДЫ СИНТЕЗА ДЕТЕРМИНИРОВАННЫХ СИСТЕМ
145
4. МЕТОДЫ СИНТЕЗА ДЕТЕРМИНИРОВАННЫХ
СИСТЕМ
Рассматривается синтез обратных связей для объектов
с сосредоточенными параметрами и различных целевых усло-
вий - заданного распределения корней характеристического
уравнения замкнутой системы (модальное управление), мини-
мума интегральных или суммарных функционалов (опти-
мальное управление), минимума функционалов мгновенных
ошибок (локально-оптимальное управление). Даны примеры
синтеза для объектов с сосредоточенными и распределенны-
ми параметрами.
4.1. Синтез следящих систем
Важной задачей создания систем автоматического управле-
ния является
синтез управлений, обеспечивающих достижение
целевого условия: 0)()(
⎯
⎯
→
⎯
−
=
∞→t
зад
tyyte , где
зад
y
– заданное
значение выхода;
)(
t
y – выходня координата системы.
Определение 4.1.1. Величина )(
t
e называется динамиче-
ской ошибкой
САУ.
Была отмечена важность использования сигнала ошибки для
управления объектами, что приводит к применению отрицатель-
ной обратной связи. Проанализируем влияние обратной связи на
характеристики систем на примере сравнения двух систем управ-
ления объектом с передаточной функцией W(s): разомкнутой
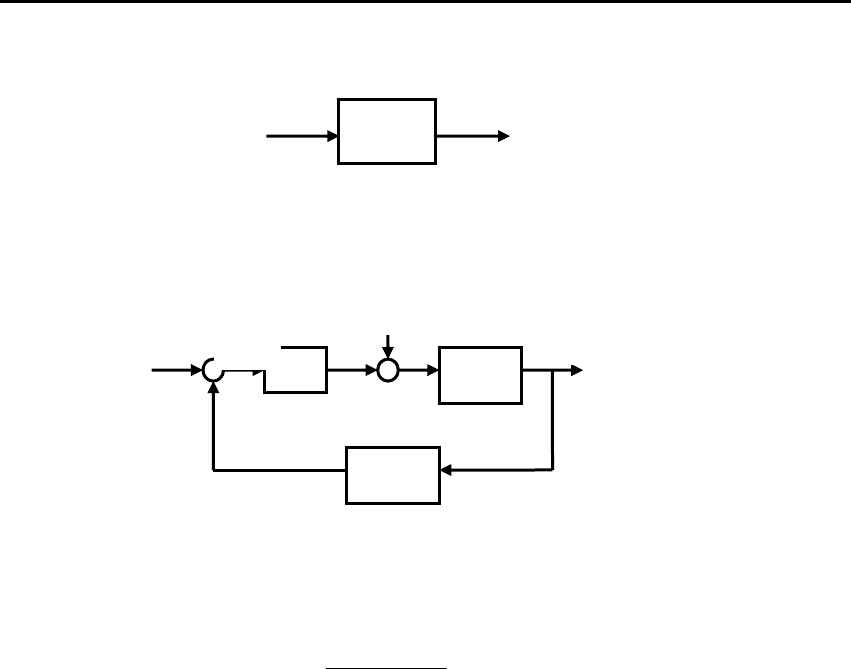
(рис. 4.1.а) и замкнутой (рис. 4.1.б). В разомкнутой САУ динами-
ческая ошибка мо
жет быть малой лишь при близости передаточ-
ной функции к единице:
[
]
)()(1)( sysWse
зад
−
=
.
Изображение по Лапласу ошибки управления замкнутой САУ
определяется равенством:
146
Рис. 4.1. Структуры синтезируемых разомкнутой и замкнутой систем
)(
)(1
1
)(
sy
sW
se
зад
p
+
=
,
где )()()( sHsWKsW
p
= – передаточная функция разомкнутой
системы. Очевидно, что с увеличением коэффициента усиления K
значение ошибки уменьшается. Предел увеличения коэффициен-
та усиления определяется требованием устойчивости САУ. Один
из важных показателей систем автоматического управления – ус-
тановившаяся ошибка системы.
Определение 4.1.2. Установившаяся ошибка – это ошиб-
ка, существующая после окончания переходного процесса, вы-
званного внешним возмущающим (возмущением) или управ-
ляющим (управлением) воздействиями .
Для вычисления статической ошибки можно использовать
теорему о конечном значении:
0
lim lim ( ).
ts
s
es
→∞ →
=
⋅
W
(
s
)
Н(s)
K
)(sy
зад
)(se
—
)(sw
)(sy
—
б)
W(s)
)(sy
)(sy
зад
a)

4. МЕТОДЫ СИНТЕЗА ДЕТЕРМИНИРОВАННЫХ СИСТЕМ
14
7
При отсутствии нулевых корней передаточной функции
W(s) и при входном воздействии
)(1)( tty
зад
=
установившаяся
ошибка
определяется равенством:
1).
Для разомкнутой САУ (рис. 4.1.а):
[]
)0(1
1
)(1
lim
)(
0
W
s
sWse
s
−=⋅−=∞
→
,
2). Для замкнутой САУ – системы с обратной связью (рис.
4.1.б):
)0(1
11
)(1
1
lim
)(
0
WKssWK
se
s
+
=
+
=∞
→
.
Значение
0
)(
=s
sW часто называют коэффициентом усиле-
ния на нулевой частоте
(по постоянному сигналу). Полученные
соотношения свидетельствуют о снижении динамических и уста-
новившихся ошибок в замкнутых САУ за счет обратных связей.
Параметры объекта управления изменяются, что приводит к
изменению его передаточной функции. Анализ влияния измене-
ния параметров передаточной функции на выходной сигнал про-
водится следующим образом. Пусть передаточная функция объ-
екта имеет вид:
)()()(
0
sWsWsW
Δ
+
=
,
где )(
0
sW – базовое значение передаточной функции, а
)(
s
WΔ
– ее
изменение, вызванное отклонением параметров в процессе рабо-
ты. Тогда для разомкнутой системы изменение выходного сигна-
ла
)()()( sysWsy
зад
Δ=Δ
.
В замкнутой системе управления, где изображение по Лап-
ласу выходного сигнала определяется равенством:

148
)(
))()(()(1
))()((
)()(
0
0
sy
KsWsWsH
sWsWK
sysy
зад
Δ++
Δ
+
=Δ+
,
его изменение существенно уменьшается. При выполнении усло-
вия
)()(
0
sWsW <<Δ можно получить:
()
)(
)()(1
)(
)(
2
0
sy
sWsHK
sWK
sy
зад
+
Δ
=Δ .
Рассмотрим влияние возмущения
()wt
на выходной сигнал
системы автоматического управления. Для этого рассмотрим
ошибку, вызванную возмущением, при нулевом задающем воз-
действии
0
=
зад
y и докажем соответствующее утверждение. В
системе без обратной связи с возмущением, приведенным к вхо-
ду, изображение ошибки и ее установившееся значение при
w(t)=1(t) определяются совокупностью следующих равенств:
)()()(
s
w
s
W
s
e −= ,
[]
)0(
1
)(
lim
)(
0
W
s
sWse
s
−=−=∞
→
.
Для замкнутой САУ при таких условиях получим следующие со-
отношения для изображения ошибки:
)(
)(1
)()(
)( sw
sW
sHsW
se
p
+
−=
,
)0()0(1
)0()0(1
)()(1
)()(
lim
)(
0
HWK
HW
ssHsWK
sHsW
se
s
+
−
=
+
−
=∞
→
.
Утверждение 4.1.1. Если передаточную функцию обратной
связи
)(sH
выбирают близкой к единице, и в рабочем диапазоне
частот выполняется соотношение:
1)( >>sW
p
, то ошибки в замк-
