Козлов В.Н., Куприянов В.Е., Шашихин В.Н. Управление энергетическими системами. Часть1. Теория автоматического управления

Подождите немного. Документ загружается.

4. МЕТОДЫ СИНТЕЗА ДЕТЕРМИНИРОВАННЫХ СИСТЕМ

159

ратной связью

,)(

uu = ,)(

xuu

(4.12)

обеспечивающие минимум интегрального (для непрерывной сис-

темы) или суммарного (для дискретной системы) функционала

(4.11) и стабилизацию САУ. Такая задача называется

задачей

оптимальной стабилизации.

Для решения задачи используем

необходимые условия оптимальности, следующие из метода

динамического программирования Р. Беллмана.

4.4.2. Общий метод синтеза. Рассмотрим вывод функцио-

нального

уравнения Беллмана как необходимого условия оп-

тимальности

для задачи оптимальной стабилизации. Пусть

уравнение возмущенного движения объектов имеет вид (4.10)

),,(



а функционал качества определяется соответствующим выраже-

нием (4.11). Введем функцию Ляпунова–Беллмана аргументов t и

х(t) и рассмотрим ее значения для моментов t и (t+s):

⎥

⎦

⎤

⎢

⎣

⎡

Φ+=

∫

ttxduxtxV )),((),,(min),(

ττω

, (4.13)

⎥

⎦

⎤

⎢

⎣

⎡

Φ+=++

∫

ttxduxststxV )),((),,(min)),((

ττω

. (4.14)

Управление u должно доставлять минимум J для любого значе-

ния s > 0. Следовательно, уравнение (4.13) для любого значения s

> 0 можно переписать с учетом (4.14) в преобразованном виде

⎥

⎦

⎤

⎢

⎣

⎡

+++=

∫

+st

ststxVduxttxV )),((),,(min)),((

ττω

. (4.15)

160

Если V(. , .) – гладкая функция, то существует предел

ttxVststxV



∂

−

→

)),(()),((

lim

Учитывая это, а также независимость V от u можно из функцио-

нального уравнения (4.15) получить преобразованное уравнение:

)),(()),((

),,(

min

***

ttxVststxV

tux

⎥

⎦

⎤

⎢

⎣

⎡

−

(4.16)

где )(

⋅

– значение, соответствующее теореме о среднем для

интеграла в равенстве (4.15). После сокращения в выражении

(4.16) на s и перехода к пределу при s→0 получим

необходимое

условие оптимальности – уравнение Беллмана

min ( ) ( , , ) 0,

Vx xut

⎡⎤

⎣⎦



(4.17)

обеспечивающего минимум интегрального функционала в (4.11)

для открытой области изменения

∈

. Если область определе-

ния ограничена (

Du ∈ ), то уравнение (4.17) запишется в виде:

[

]

0),,()(inf

∈

tuxxV



. (4.18)

Основную роль в уравнениях (4.17) и (4.18) играет функция

V(x(t),t), которая является

функцией Ляпунова, удовлетворяющей

граничным условиям:

)),(()),((

kkkk

ttxttxV

при

∞

t ;

0)),(( =

ttxV для ∞=

t .

Уравнение Беллмана для дискретных систем имеет вид:

,0)],,([min

Δ tuxV

ttt

(4.19)

где

VΔ – приращение функции Ляпунова на траекториях (4.10).

4. МЕТОДЫ СИНТЕЗА ДЕТЕРМИНИРОВАННЫХ СИСТЕМ

161

4.4.3. Синтез оптимальных управлений для линейных

объектов.

Рассмотрим линейные уравнения динамики непрерыв-

ных и дискретных объектов, имеющие следующие формы для:

непрерывных объектов:

,)0(,

xxuBxAx =+=



дискретных объектов:

ttt

Ax Bu x x

+= (4.20)

Пусть интегральные и суммарные функционалы (4.11) равны:

()

∫

∞

+= dtuRuxQxJ

(

)

∑

∞

uRuxQxJ

(4.21)

где 0,0 >=≥=

RRQQ .

Предполагается, что объект вполне управляемый. Найдем

управления с обратной связью, минимизирующие функционалы

(4.21) на траекториях систем (4.20). Представим уравнения Белл-

мана (4.17) и (4.18) для непрерывных и дискретных систем в со-

ответствующих формах, которые имеют соответствующие виды:

для непрерывных объектов для дискретных объектов

0)(min =++

∈

uRuxQxV



min(

)0.

tttt

xQx uRu

∈



Выберем функции Ляпунова для непрерывных и дискретных

объектов в виде соответствующих квадратичных форм:

,)( xPxxVV

,)(

ttt

xPxxVV == (4.23)

где 0>=

PP . Для преобразования необходимых условий (4.22)

вычислим полную производную

)(xV



и приращение

VΔ в силу

уравнений объекта управления

. Тогда можно получить два

(4.22)

162

класса уравнений для непрерывных и дискретных систем, полу-

ченные вычислением полной производной или приращения функ-

ций Ляпунова в силу исследуемых систем. Получим для непре-

рывных и дискретных систем соответствующие полные произ-

водные и приращения, вычисленные в силу уравнений:

для непрерывных объектов:

() 2,

TT TTT TT

xAxBu

VxPxxPx xAPxxPAxuBPx

=+ = ++





для дискретных объектов:

()

ttt

t t t t t x Ax Bu

TT T TT TT

tttttttt

VxPx xPx

A P Ax x Px u B PAx u B PBu

++ =+

=− =

=−+ +



Далее необходимо подставить полную производную функ-

ции Ляпунова

)(xV



и приращение функции Ляпунова

VΔ в соот-

ветствующие (непрерывные и дискретные) уравнения Беллмана

(

как необходимые условия экстремума оптимизации).

В результате можно получить преобразованные уравнения

Беллмана как необходимые условия оптимальности для рассмат-

риваемых задач оптимизации в непрерывном и дискретном вре-

мени. Условия оптимальности, соответствующие непрерывному

и дискретному времени обладают специальной правой частью,

представляющей собой конечномерную экстремальную задачу:

.0)

2(min

,0)2(min

=+++

++−

=++++

∈

TTTTTTT

uRuxQxuPBBu

xAPBuxPxxAPAx

uRuxQxxPBuxPAxxPAx

(4.24)

4. МЕТОДЫ СИНТЕЗА ДЕТЕРМИНИРОВАННЫХ СИСТЕМ

163

Вычислим минимум в левых частях полученных уравнений

Беллмана для непрерывных и дискретных систем, используя пра-

вила векторного дифференцирования линейной и квадратичной

форм вида:

()

(

)

MxxMxcxc

2, =

′

. Используя необходимое

условие экстремума, можно получить линейные алгебраические

уравнения для непрерывных и дискретных объектов:

,022 =+ uRxPB

0222 =++

uRuBPBxPAB

Тогда минимизирующие элементы

u примут вид:

PxBRu

T−

−=

xPABRu

−

−= (4.25)

.BPBRR

При подставке управлений

u и

в уравнения динамики непре-

рывных и дискретных объектов (4.24) можно получить уравнения

для непрерывного (слева) и дискретного (справа) времени:

,0][

=+−+

−

xQPBPBRPAPAx

TTT

.0]

[

=+−

−−

−

xQPABRPBA

PAPAx

Для выполнения полученных равенств при любых векторах

x необходимо, чтобы выполнялись матричные уравнения:

QPBPBRPAPA

−=−+

−

PBBRR

QPABRPBA

PAPA

−=−

−−

−

(4.26)

которые называются уравнениями Риккати относительно мат-

рицы Р для непрерывных и дискретных систем. Решения матрич-

ных нелинейных алгебраических уравнений (4.26) не единствен-

164

ны. Необходимо с помощью численных методов найти решение,

которое является положительно определенной матрицей. Суще-

ствование такого решения определяется следующей теоремой.

Теорема 4.4.1. Для существования единственного поло-

жительно определенного решения алгебраического уравнения

Риккати достаточно

выполнения условий:

1). Пара матриц (A,B) должна быть невырожденной, т.е. объект

(4.20) с параметрами A, B – вполне управляемый;

2). Матрица R>0 (матрица – положительно-определенная);

3). Требуется выполнение одного из двух условий:

а). Матрица

0>Q - положительно-определенная матрица;

б). Матрица 0

≥Q и представима в виде CCQ

= , причем пара

),(

CA - невырожденная.

Таким образом, оптимальные управления осуществляется

регуляторами пропорционального типа (4.12) (

xKu =

, )

Kxu =

∗

параметры которых определяются уравнениями (4.26) так, что:

для непрерывных систем

PBRK

T−

−=

для дискретных систем

PABRK

−

−=

Приведенные результаты являются решением задачи опти-

мальной стабилизации и основой для синтеза оптимальных регу-

ляторов.

4.5. Наблюдаемость объектов и систем

Синтезированные ранее в п. 4.3 и 4.4 законы управления ос-

нованы на использовании для управления координат состояния

объекта. Известно, что координаты состояния часто не могут

быть измерены и возникает задача восстановления координат со-

стояния по измерениям выходных координат

)(

или

y .

4. МЕТОДЫ СИНТЕЗА ДЕТЕРМИНИРОВАННЫХ СИСТЕМ

165

Определение 4.5.1. Объекты (4.10) называются вполне на-

блюдаемыми

, если по точным измерениям векторов выхода )(

и входа

)(

u (или

y и

u ), а также их производных (конечных

разностей) можно определить оценки векторов состояния непре-

рывных объектов

()



или дискретных объектов



, такие, что

выполняется условия

(

)

(

)

lim

txt

→∞



для непрерывного объекта и

lim

→∞



для дискретного объекта. Для оцениваниякоординат

состояния по выходным координатам необходимо выполнение

критериев наблюдаемости.

Теорема 4.5.1 (критерий наблюдаемости для линейных

систем). Для того чтобы объекты

,, uD

CyuB

+=+=



ttt

uDxCy

uBxAx

(4.27)

были вполне наблюдаемыми, необходимо и достаточно выполне-

ние рангового критерия

nCACACACrank

TnTTTTTT

−

])(||)(||[

 ,

)(dim

. (4.28)

Рассмотрим доказательство достаточности (4.28) для непре-

рывных объектов. Поскольку

)(

u измеряется и параметры моде-

ли (4.27) известны, можно ограничиться вариантом D=0. Про-

дифференцируем вектор выхода (n–1) раз. Тогда:

uCBCABuxCAuCBxCAy

CBuCAxxCy

Cxy

BuAxx

′

++=

′

′′

′

166

∑

−

−−−−

′′

′

++=

′′

′′′

)2(1)1(

lnlnn

BuCAxCAy

uCBuCABBuCAxCAy



Представим подчеркнутые слагаемые системы через остальные

переменные рассматриваемой системы. Тогда можно получить

следующие соотношения:

()

232

nlnl

CAx

CBu

CA x

CABu CBu CA x

CA Bu CABu CBu

CA x y CA Bu

−

−−−

′

==−

′′ ′ ′′′ ′ ′′

=− − =− − −

=−

∑

………

(4.29)

Система линейных алгебраических уравнений (4.29) разре-

шима относительно координат вектора состояний x, если ранг

матрицы системы равен n:

nCACACACrang

−

]...[

Поскольку при транспонировании ранг матриц не изменяется, то

доказана достаточность условия полной наблюдаемости (4.28).

Определение 4.5.2. Устройства, используемые для вычис-

ления координат состояния по измерениям выходных координат,

называются

наблюдателями состояния.

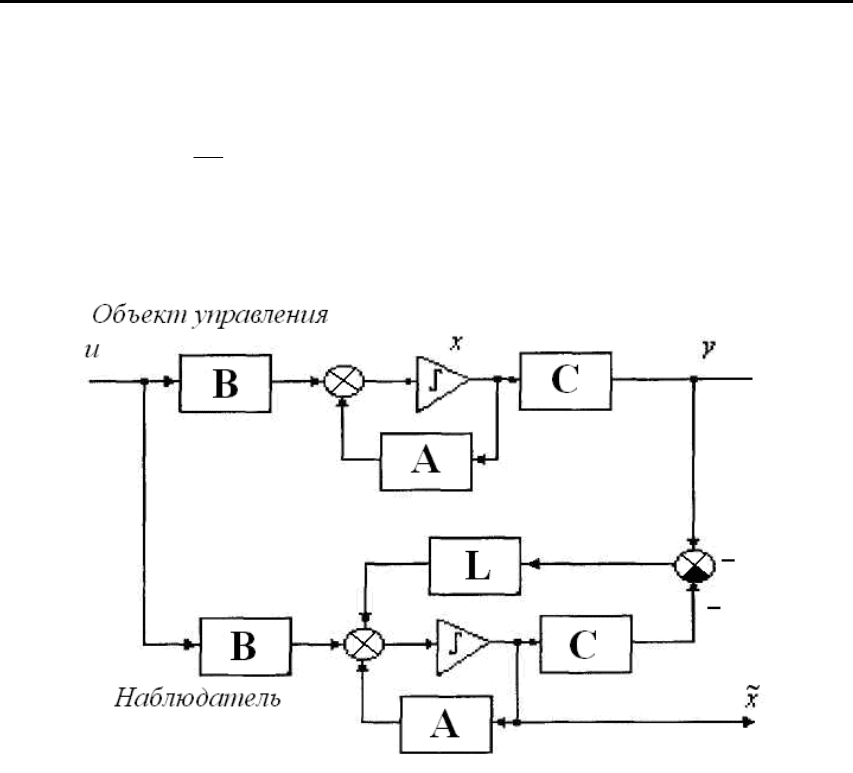
Известны разомкнутые и замкнутые наблюдатели, причем

структурная схема таких устройств, предложенная Люенберге-

ром, описывается уравнениями

(

, xCxCLuBxAxuBxAx

−



(4.30)

4. МЕТОДЫ СИНТЕЗА ДЕТЕРМИНИРОВАННЫХ СИСТЕМ

Структурная схема наблюдателя Люенбергера, соответствующая

уравнениям (4.30), представлена на рис. 4.2. Изменение ошибки

наблюдателя

)(

)()( txtxte



−=

определяют на основе использо-

вания соотношений (4.30), что приводит к уравнению ошибки:

Рис. 4.2. К структуре наблюдателя Люенбергера

.)( eL

e −=



При синтезе систем с наблюдателями управление

строится в функции оценки

. Тогда уравнения объекта и

наблюдателя определяются уравнениями:

)(

xBKxLCxLCAxxBKxAx ++−=+=



Введение ошибки преобразует уравнения наблюдателя к виду:

.)(,)( eLCAeeBKxBKAxx −=−+=



(4.31)

Если ввести вектор

[,]

zxe=

, то системе (4.31) соответствует

однородное дифференциальное уравнение с блочной матрицей

168

ABK BK

zAz A

+−

⎡

⎤

⎢

⎥

−

⎣

⎦



При этом матрица A

замкнутой системы имеет такие же собст-

венные значения, что и стоящие на главной диагонали блоков

+ и L

− . Таким образом доказано утверждение.

Утверждение 4.5.1. Если система (4.27) управляемая и на-

блюдаемая, то можно выбрать матрицы K и L так, что обратная

связь

= с наблюдателем (4.30) стабилизирует систему.

Таким образом, для наблюдаемых объектов синтезируются

наблюдатели для оптимальной стабилизации и других задач.

4.6. Синтез стабилизирующих регуляторов

на основе мо

делей «вход–выход»

При проектировании определенного класса систем управле-

ния стремятся использовать наиболее простую зависимость

управления от выходных переменных. Желательно строить

управление в функции выхода в наиболее простой форме

u = ,

однако далеко не всегда это приводит к успеху. Рассмотрим воз-

можность построения устойчивых систем управления с заданны-

ми полюсами передаточной функции при управлении по выходу.

4.6.1. Постановки задач. Пусть заданы математические мо-

дели вполне управляемых непрерывных и дискретных объектов в

виде соотношений «вход–выход», которые представляются урав-

нениями:

для непрерывного времени

,)()()()(

upb

ypa

для дискретного времени

,)()(

ubya

(4.32)

где

ΔΔ

- операторы дифференцирования и сдви-