Ковтун В.В., Павлов В.С., Дорофєєв О.А. Опір матеріалів. Розрахункові роботи
Подождите немного. Документ загружается.

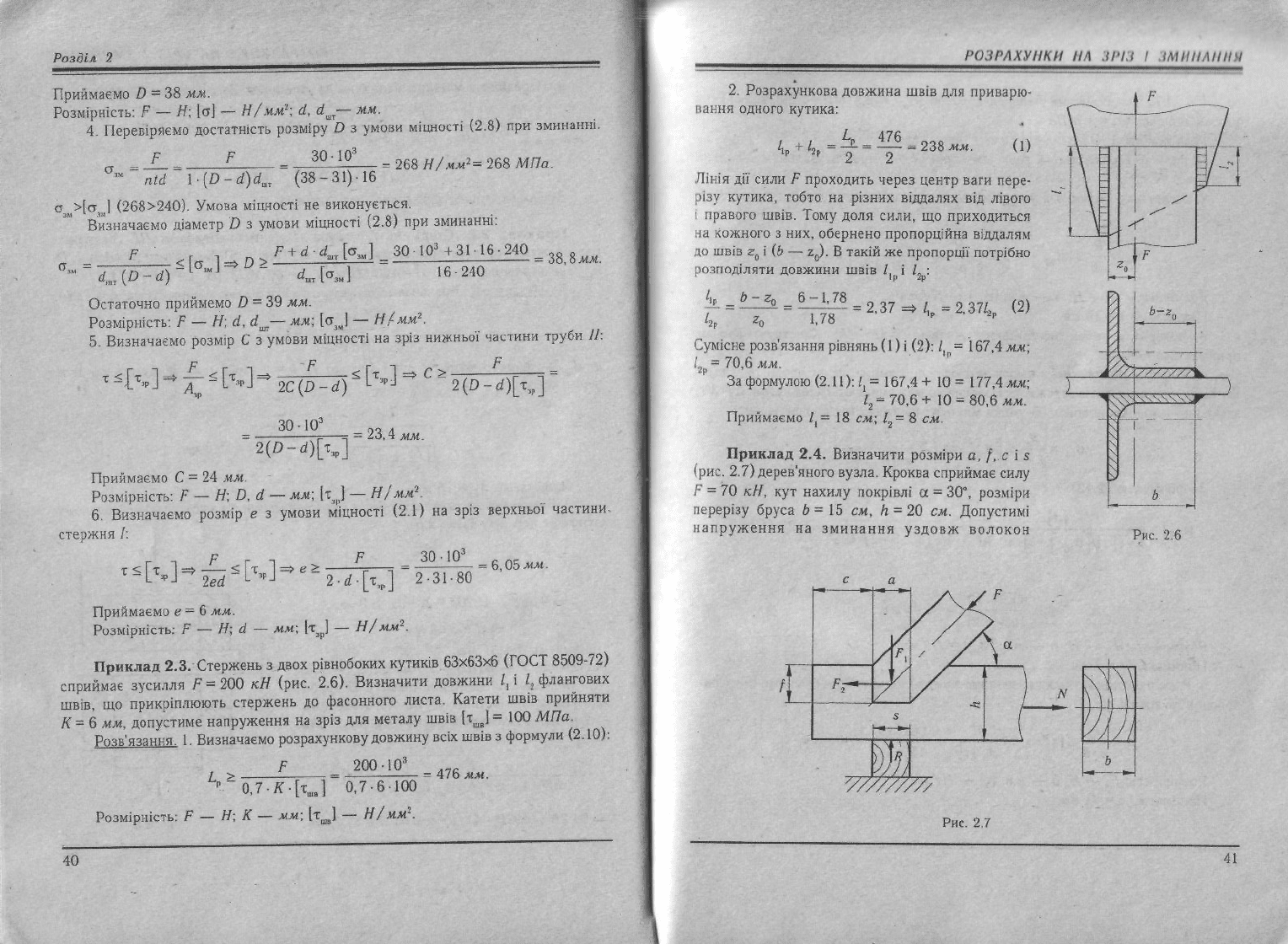
Розділ
2
Приймаємо
D = 38 мм.
Розмірність: F ~ И; [а] — Н/мм
2
; d,
d
at
—
мм.
4. Перевіряємо достатність розміру D з умови міцності (2.8) при зминанні.
(У...
=
F
пій
30-10
3
•
= 268Я/лш
2
=268 МПа.
\{D-d)d
a
,
(38 - З і) 16
о
=и
>[(т
іч
| (268>240). Умова міцності не виконується.
Визначаємо діаметр D з умови міцності (2.8) при зминанні:
D>
ЗО
-1O
3
+ 31 -16 -240
16-240
Остаточно приймемо D - 39 мм.
Розмірність: F — H;d, d
m
_— мм; [и J — Н/мм
г
.
5. Визначаємо розмір С з умови міцності на зріз нижньої частини труби //:
F
2С (D - d)
30
•
ІО
3
C>
=
23,4
мм.
Приймаємо
С - 24 мм.
Розмірність: F — И; D. d — мм; Іт
з
] — Н/мм
1
.
6. Визначаємо розмір є з умови міцності (2.1) на зріз верхньої частини,
стержня /:
<к,
Г і
т.
ЗОЮ
3
"
2-31-80
=
6,05 мм.
Приймаємо
(t = 6 мм.
Розмірність: F — Ні d — мм; [т
зі
] — Н/мм
2
.
Приклад
2.3. Стержень з
двох
рівнобоких кутиків
63x63x6
(ГОСТ
8509-72)
сприймає зусилля F - 200 кИ (рис. 2.6). Визначити довжини /, і t
2
флангових
швів, що прикріплюють стержень до фасонного листа. Катети швів прийняти
К = 6 мм, допустиме напруження на зріз для металу швів [т
іав
1 = 100 МПа.
Розв'язання.
1. Визначаємо розрахункову довжину
всіх
швів з формули (2.10):
F 200
-
10
а
-
= 476 мм.
Розмірність: F — Н; К — мм; [т
шв
] — Н/мм
2
.
40
РОЗРАХУНКИ ІІЛ ЗРГ.І І ЛМШІАШШ
2. Розрахункова довжина швів для приварю-
иання
одного кутика:
Лінія дії сили F проходить через центр ваги пере-
різу кутика, тобто на різних
віддалях
від лівого
і
правого швів. Тому доля сили, що приходиться
на
кожного з них. обернено пропорційна віддалям
до швів г
0
і (і — z
0
). В такій же пропорції потрібно
розподіляти довжини швів /
i|r
i l
2r
:
b-z
0 =
6 - 1,78
z
Q
" 1,78
=
2,37 =* і =2,374„ (2)
Сумісне розв'язання рівнянь (1) і (2): І, -
167,4лл;
/,
(
= 70,6 мм.
За
формулою (2.11):^= 167,4+ 10=
177,4мм;
/
г
=70,6+
10 = 80,6 мм.
Приймаємо
/, = 18 см; /
2
= 8 см.
Приклад
2.4. Визначити розміри a, f, с \ s
(рис.
2.7) дерев'яного
вузла.
Кроква сприймає силу
F = 70 к.Н, кут нахилу покрівлі а = 30", розміри
перерізу
бруса
6=15 см. ft = 20 см. Допустимі
напруження на зминання уздовж волокон
Рис.
2.7
Рис.
2.6
41

Розділ
2
[c
a
j
= 8
МПа,
на
зминання поперек волокон Іо
м
.]
= 2,5 МПа і на
сколювання
уздовж волокон
[т] = 1 МПа.
Розв'язання.
1.
Розкладемо силу
F на
складові
F
t
і F
r
Ці
сили зрівноважуються реакцією опори
R
=
F
f
і
розтягувальним зусиллям
в затяжці
N
= F
s
.
2. Визначимо розмір
s з
умови міцності при зминанні затяжки силою
R по
площі
sb:
R
35
•
10
3
= 93,3 мм.
"»%
fe
n^J--
&
|--^]-
1
5o.2,5
Розмірність:
R — H; b — мм;
іо
ет
]
—
Н/мм
2
.
Приймаємо
s
=
10 см.
3. Розмір
а, з
умови рівноміцності дорівнює
s {F
y
-
R). Конструктивно
він
приймається більшим.
4. Розмір
/
визначимо
з
умови міцності
при
зминанні
по
площі
fb у
місці
контакту торця крокаи
із
затяжкою. Волокна крокви зминаються під кутом
а
=
30°,
затяжки
—
уздовж волокон.
З
умови міцності
на
зминання крокви маємо:
За
формулою (2.12):
МПа.
Тоді
60,62-10'
-
64,45мм.
'
~
150-6,27
Розмірність:
Fj — Н; b — мм;
[сг^.]
=
Н/мм
2
.
Приймаємо
/
=
7 см.
5, Розмір
с
кінця затяжки визначимо
з
умови міцності прн сколюванні уздовж
волокон
по
площі
cb:
Л
г
, Л
60,62-10
3
Розмірність:
F
2
—
H;
b —
мм; [т]
—
Н/мм
1
.
Приймаємо
с
= 41
см.
=
404
мм.
42
РОЗРАХУНКИ
НА
ЗРІЗ
І
ЗМИНЛИНЯ
2.2.3.
ЗАДАЧІ
ДЛЯ
САМОСТІЙНОГО
РОЗВ'ЯЗАННЯ
2.1. Перевірити міцність заклепкового з'єднання, якщо діаметр заклепка
(І
=
20мм
(рис. 2.8),
Н=
160МЯа,|т
!р
|= ПОЛШа,
[oj -
320 МПа.
Відповідь:
о=і56,3
МПа;
т
і1(
= 99,5
МПа;
(т_,™=
312,5
МПа.
Міцність
•л
єднання забезпечена.
2.2.
З
умови рівноміцності визначити розміри головки
D і h
стержня,
по-
казаного на рис. 2.9, при допустимих напруженнях: [о]
=
140 МПа;
[т ]
= ІООЛІЯа;
|я
J = 250
АШа.
Відповідь:
D
=
42 мм; h = 11 мм.
F = 250 кН
Рис.
2.8
h
f
CM
II
•о
v
///
Рис.
2.9
Рис,
2.10
43
Розділ
2
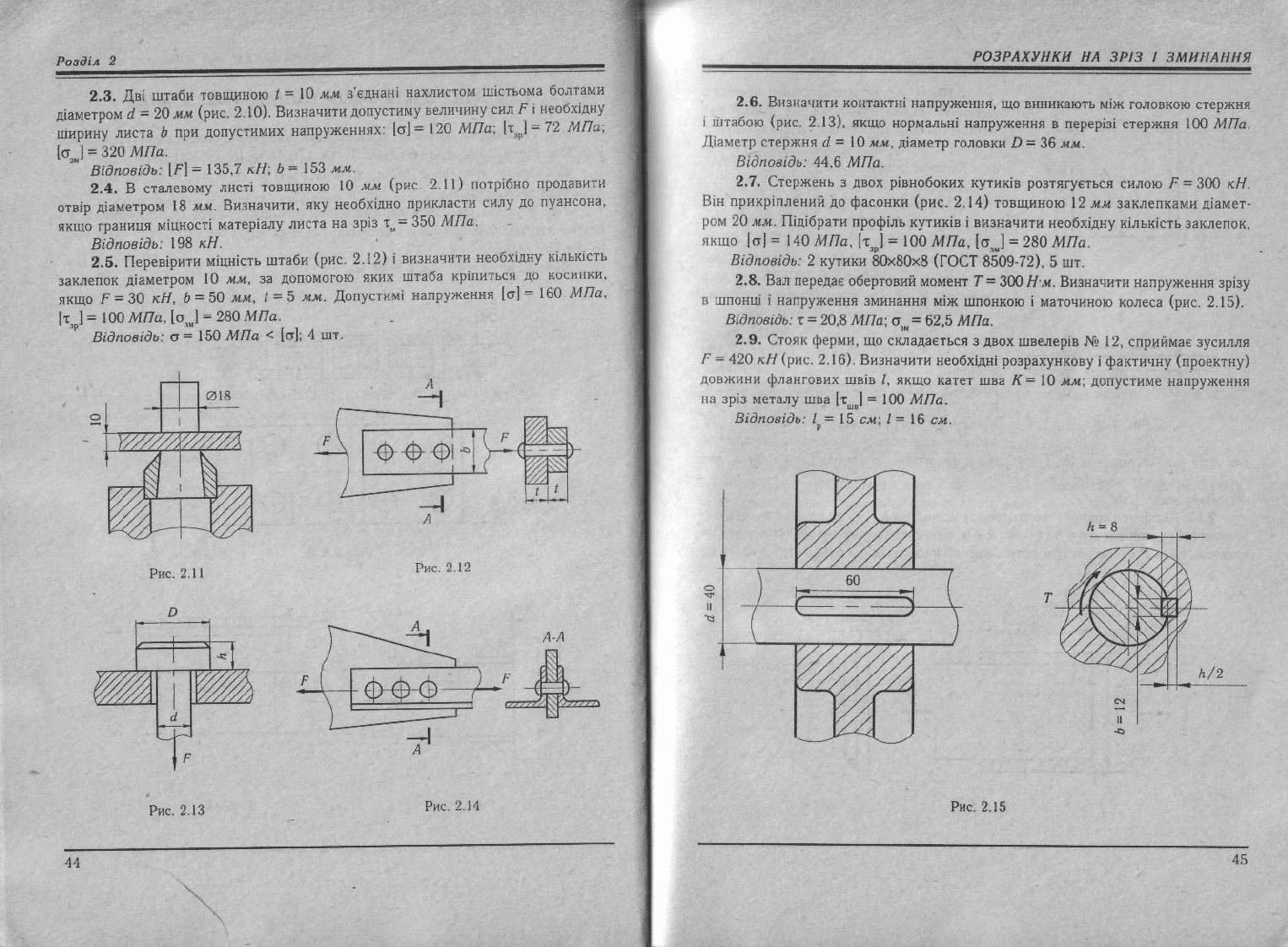
2.3. Дві штаби товщиною t = 10 мм з'єднані нахлистом шістьома болтами
діаметром d - 20 мм (рис. 2.10). Визначити допустиму величину сил F і необхідну
ширину листа Ь при допустимих напруженнях: \а\ = 120 ЛІЯа; |т
ч
| = 72 МЯо:
[oj = 320 МЯа.
Відповідь:
[F] = 135,7 «Я: Ь = 153 лш.
2.4. В сталевому листі товщиною 10 мм (рис. 2.11) потрібно продавити
отвір діаметром 18 мм. Визначити, яку необхідно прикласти силу до пуансони,
якщо
границя міцності матеріалу листа на зріз т
и
= 350 МПа.
Відповідь:
198 кН.
2.5. Перевірити міцність штаби (рис. 2.12) і визначити необхідну кількість
заклепок
діаметром 10 мм, за допомогою яких штаба кріпиться до косинки.
якщо
F — ЗО кН, 6 = 50 мм, ( = 5 мм. Допустимі напруження [о] = 160 МПа,
іт
р
]=
Ю0ЛіЯа,[а
ірі
] = 280МЯа.
Відповідь:
а — 150 МПа < [а]; 4 шт.
018
Рис.
2.12
Л-А
Рис.
2.13
Рис.
2.14
\
РОЗРАХУНКИ
НА
ЗРІЗ
І ЗМИНАННЯ
2.6. Визначити контактні напруження, що виникають між головкою стержня
і
іптабою {рис. 2.13), якщо нормальні напруження в перерізі стержня 100 МПа.
Діаметр стержня d = 10 мм, діаметр головки D = 36 мм.
Відповідь:
44,6 МПа.
2.7. Стержень з двох рівнобоких кутиків розтягується силою F - 300 кН.
Він прикріплений до фасонки (рис. 2.14) товщиною 12 мм заклепками діамет-
ром 20 мм. Підібрати профіль кутиків і визначити необхідну кількість заклепок,
якщо
Істі
=
[АОМПа,
[т
ар
] = 100 МПа, \aj = 280 МПа.
Відповідь:
2 кутики
80x80x8
(ГОСТ
8509-72). 5 шт.
2.8. Вал передає обертовий момент Т = 300Им. Визначити напруження зрізу
в
шпонці і напруження зминання між шпонкою і маточиною колеса {рис. 2.15).
Відповідь:
т - 20,8 МПа; о
зм
= 62,5 МПа.
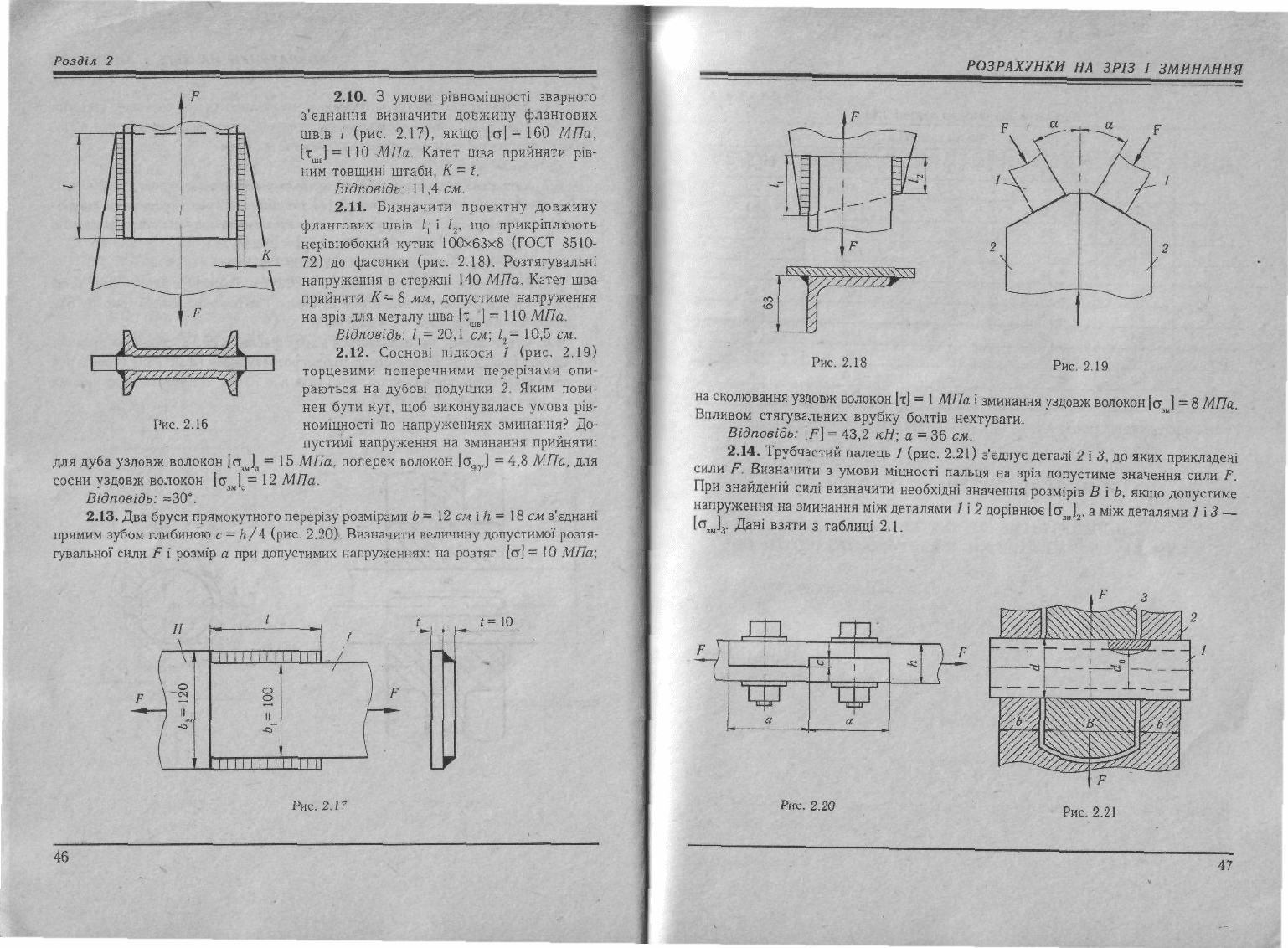
2.9. Стояк ферми, що складається з двох швелерів № 12, сприймає зусилля
F = 420 кН (рис. 2.16). Визначити необхідні розрахункову і фактичну (проектну)
довжини флангових швів І, якщо катет шва К= 10 мм; допустиме напруження
на
зріз металу шва [т
шв
] = 100 МПа.
Відповідь:
1„= 15 см; І- !6 см.
60
Рис.
2.15
45
Розділ
2
Рис.
2.16
2.10. З
умови
ріаноміцності
зварного
з'єднання
визначити
довжину
флангових
швів
/
(рис.
2.17),
якщо
[а]= 160 МПа,
[т
ш
|=
110 МПа.
Катет
шва
прийняти
рів-
ним
товщині
штаби,
K-t.
Відповідь:
11,4 см.
2.11. Визначити проектну довжину
флангових швів (
:
і
(,, що прикріплюють
нерівнобокий
кутик
100x63x8
(ГОСТ 8510-
72) до фасонки (рис
2.18).
Розтягувальні
напруження а стержні 140 МПа. Катет шва
прийняти
К- 8 мм, допустиме напруження
на
зріз для металу шва ІТ
шв
] = 110 МПа
Відповідь:
^=20.1 7м;
І,
г
= 10,5 см.
2.12. Соснові підкоси
/
(рис. 2.19)
торцевими поперечними перерізами опи-
раються на
дубові
подушки 2. Яким пови-
нен
бути кут, щоб виконувалась умова рів-
коміцності по напруженнях зминання? До-
пустимі напруження на зминання прийняти:
Д = 15 МПа. поперек волокон |o
w
] = 4,8 МПа, для
,=
12 МПа.
для
дуба
уздовж волокон
і
сосни
уздовж волокон
[а
Відповідь:
=30°.
2.13. Два бруси прямокутного перерізу розмірами b
-
12 см і h
-
18 с.и з'єднані
прямим
зубом глибиною с =
ft/4
(рис. 2.20). Визначити величину допустимої розтя-
гувальної сили F і розмір а при допустимих напруженнях: на розтяг |о] = 10 МЛа;
=10
Рис.
2.17
46
РОЗРАХУНКИ
НА
ЗРІЗ
І
ЗМИНАННЯ
\/////////l
Рнс.
2.18
Рис.
2.19
на
сколювання уздовж волокон [т] = 1 МПа і зминання уздовж волокон [o
a
j = 8 МПа.
Впливом стягувальних врубку болтів нехтувати.
Відповідь:
\F\ = 43,2 кН; а
-
36 см.
2.14. Трубчастий палець 7 (рис. 2,21) з'єднує деталі 2 і 3, по
ЯКИХ
прикладені
сили
F. Визначити з умови міцності пальця на зріз допустиме значення сили F.
При
знайденій силі визначити необхідні значення розмірів Б
і
Ь, якщо допустиме
напруження на зминання між деталями / і 2 дорівнює 1о
эы
]
2
, а між деталями / і 3 —
[а
ім
]
3
.
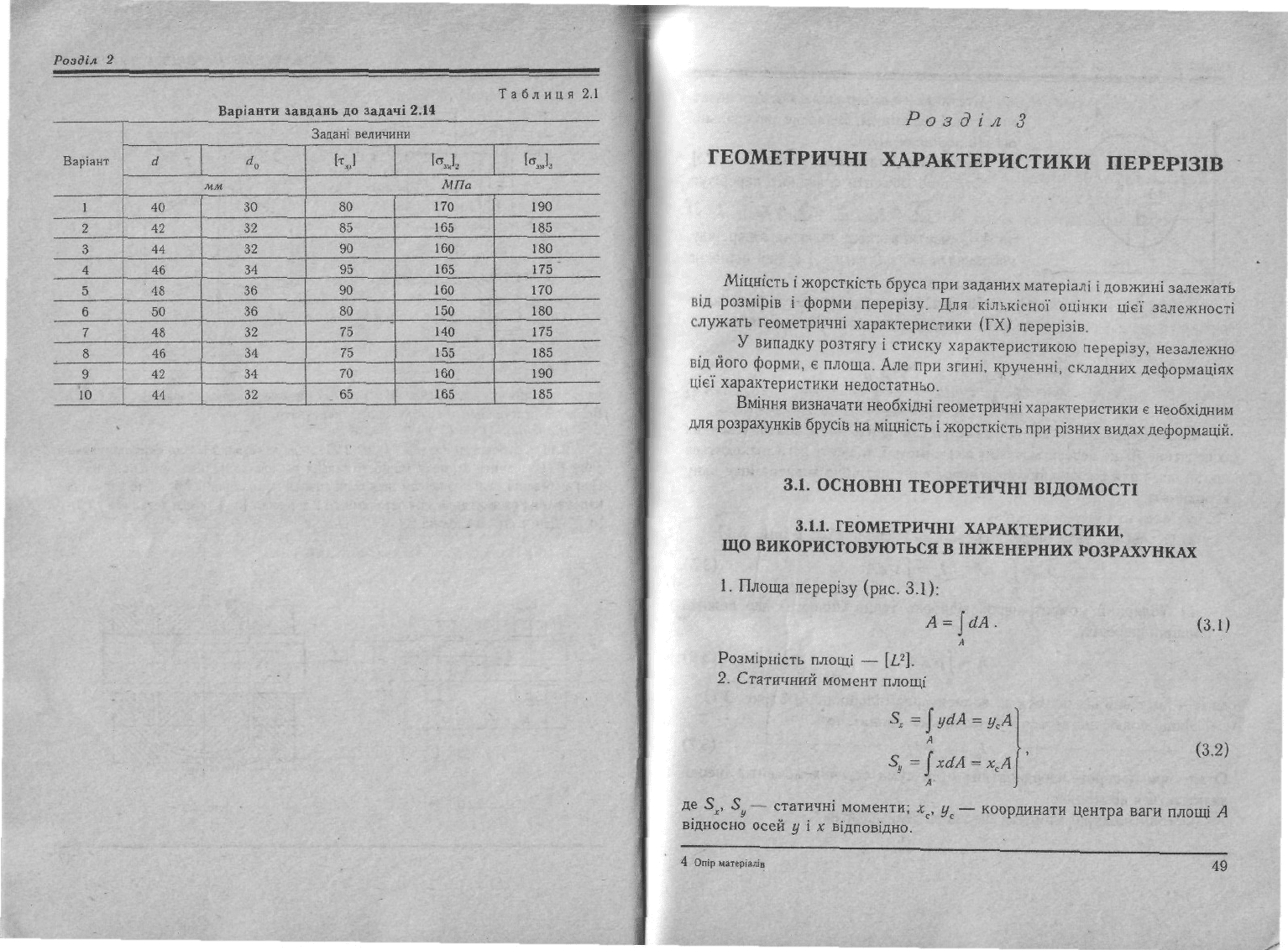
Дані взяти з таблиці 2.1.
F
З
Рис.
2.20
47
Розділ
2
Таблиця 2.1
Варіанти
завдань
до
задачі
2.14
Варіант
1
2
3
4
5
6
7
8
9
10
Задані величини
d
d
*
мм
40
42
44
46
IS
50
48
46
42
4-1
ЗО
32
32
34
36
36
32
34
34
32
К)
Kh
i<a
МПа
80
85
90
95
90
80
75
75
70
65
170
165
160
165
160
150
140
155
160
1Є5
190
185
180
175
170
ISO
175
185
190
185
Р о з д і л З
ГЕОМЕТРИЧНІ
ХАРАКТЕРИСТИКИ
ПЕРЕРІЗІВ
Міцність і жорсткість бруса при заданих матеріалі і довжині залежать
під розмірів і форми перерізу. Для кількісної оцінки цієї залежності
служать геометричні характеристики (ГХ) перерізів.
У випадку розтягу і стиску характеристикою перерізу, незалежно
від його форми, є площа. Але при згині, крученні, складних деформаціях
цієї характеристики недостатньо.
Вміння визначати необхідні геометричні характеристики є необхідним
для розрахунків брусів на міцність і жорсткість при різних видах деформацій.
3.1.
ОСНОВНІ
ТЕОРЕТИЧНІ
ВІДОМОСТІ
3.1.1.
ГЕОМЕТРИЧНІ
ХАРАКТЕРИСТИКИ,
ЩО
ВИКОРИСТОВУЮТЬСЯ
В
ІНЖЕНЕРНИХ
РОЗРАХУНКАХ
1. Площа перерізу (рис. 3.1):
=
\dA.
(3.1)
Розмірність площі — [L
2
].
2. Статичний момент площі
=
J xdA
=
х
с
А
А
(3,2)
де
-V Л~ статичні моменти; x
z
, у
с
— координати центра ваги площі А
відносно осей у і х відповідно.
4
Опір матеріям
49

Розділ
З
Рис.
3.1
Статичний
момент може
бути
як
додат-
ним,
так
і
від'ємним. Відносно центральної
осі він дорівнює нулю.
Розмірність статичного моменту
—
[L
3
].
Статичні моменти складного перерізу:
де
А. —
частина площі складного перерізу,
координати
центра ваги
х. і
і/, якої відносно
осей
х і у
відомі.
Визначення
координат центра ваги склад-
ного перерізу виконується
за
формулами:
(3.4)
Якщо
переріз має
дві осі
симетрії,
то
центр ваги знаходиться
на
їх перетині. Якщо переріз має одну вісь симетрії, то центр ваги знаходиться
на
цій осі,
і
для визначення його положення потрібно знайти лише одну
координату.
3. Моменти інерції перерізу.
а) Осьові моменти інерції перерізу відносно осей
х, у
(рис. 3.1):
;
]
у
=\хЧА.
(3.5)
б) Полярний момент інерції відносно точки (полюса),
що
лежить
в
площині перерізу:
s
dA.
(3.6)
де
р —
відстань
від
полюса
до
елементарної
площинки
dA
(рис. З.І).
Якщо
полюс збігається
з
початком координат,
то
'„
=
Л
+
V (3.7)
Отже, при повороті координатних осей сума осьових моментів інерції
залишається незмінною.
Осьові
і
полярні моменти інерції завжди додатні.
50
ГЕОМЕТРИЧНІ
ХАРАКТЕРИСТИКИ
ПЕРЕРІЗІВ
в) Відцентровий момент інерції перерізу відносно осей
х, у
(рис. 3.1):
J
1
,=jxydA.
(3.8)
А
Він може
бути
додатним, від'ємним
і
рівним нулю. Якщо
хоча
б
одна
з
двох
взаємно перпендикулярних осей
є
віссю симетрії,
то
відцентровий
момент інерції перерізу відносно таких осей дорівнює нулю.
Розмірність моментів інерції
—
[L
4
].
3.1.2.
ЗАЛЕЖНІСТЬ МІЖ
МОМЕНТАМИ
ІНЕРЦІЇ
ВІДНОСНО
ПАРАЛЕЛЬНИХ
ОСЕЙ,
ОДНІ
З
ЯКИХ
ЦЕНТРАЛЬНІ
Якщо
моменти інерції
^,,^ц,-К
л
відносно центральних осей
x
L
, y
c
(рис.
3.2) відомі,
то
моменти інерції відносно осей
х, у,
що паралельні
центральним,
визначають за формулами:
J
x
= J
Xs
+ a
2
A- J
g
= /
а<
+
йМ,
• (3.9)
]
ч=Кь
+abA
(З-
10
*
У виразі
(3.10)
потрібно врахувати знаки координат
а і Ь
центра
ваги
С
У
ч
!
І
Рис.
3.2
Рис.
3.3
51

Розділ
З
ГЕОМЕТРИЧНІ
ХАРАКТЕРИСТИКИ
ПЕРЕРІЗІВ
3.1.3.
ОБЧИСЛЕННЯ
МОМЕНТІВ
ІНЕРЦІЇ
СКЛАДНИХ
ПЕРЕРІЗІВ
Моменти
інерції складного перерізу обчислюють
як
суму
моментів
інерції його простих частин:
^Х^;
',
=
14:/
Ч
=
ХС
(зло
Величини J',,
Г
г
Г^
визначають
за
формулами (3.9), (3.10).
Якщо
в
перерізі
є
отвір, його зручно вважати частиною фігури
з
«від'ємною» площею. Наприклад, переріз, показаний на рис. 3.3, можна
розбити
на дві
прості фігури:
/
—
прямокутник bxh
і
//
—
круг діаметром
d з
«від'ємною» площею. Тоді
J.=J'.-J'J.
3.1.4.
ЗМІНА
МОМЕНТІВ
ІНЕРЦІЇ
ПРИ
ПОВОРОТІ
КООРДИНАТНИХ ОСЕЙ
Моменти
інерції перерізу відносно осей
x
v
y
y
повернутих на кут
а
від початкових осей
х,
у
(рис. 3.4):У,
].
=
і,
cos
2
а
+ /,
sin
2
a-J
sin2ctl
J
v
=
J
x
sin
s
a
+
J
y
cos
2
а
+ J
xj/
sin 2cc
I
—
S
/
=-i 2
;
(3.12)
(3.13)
Рис.
3.4
Додатним
напрямком
відліку
кута
вважа-
ють
напрямок
проти
ходу
годинникової
стрілки.
3.1.5.
ГОЛОВНІ ОСІ
І
ГОЛОВНІ
МОМЕНТИ
ІНЕРЦІЇ
Головними
називаються ортогональні осі, відносно яких відцентровий
момент інерції дорівнює нулю,
а
осьові моменти інерції набувають екстре-
мальних значень.
52
Кут
a
n
, що
визначає положення головних осей, обчислюють
за
.•нрмулою:
2/,..
tg2cc
0
=
(3.14)
Моменти
інерції відносно головних осей називаються головними мо-
•птами
Інерції
і
обчислюються
за
формулою:
(3.15)
Одна
з
головних осей нахилена на кут с^ до осіл(|а„|
<
45°],
друга
—
перпендикулярна
до
неї. Вісь
з
найбільшим моментом інерції
«ближча»
до тієї
з
осей
(х
або у), відносно якої момент інерції більший (У
г
або
/ ).
Практичне
значення мають головні осі, що проходять через центр
наги
перерізу. Вони називаються
головними
центральними
осями.
Л моменти інерції відносно
цих
осей
—
головними
центральними
моментами
інерції.
їх і
використовують
у
розрахунках.
3.1.6.
ЧАСТКОВІ
ВИПАДКИ
ВИЗНАЧЕННЯ
ПОЛОЖЕННЯ
ГОЛОВНИХ
ЦЕНТРАЛЬНИХ
ОСЕЙ
1. Переріз має одну вісь симетрії
—
одна
з
головних центральних осей
і" віссю симетрії,
друга
проходить через центр ваги перпендикулярно до першої.
2. Переріз має
дві осі
симетрії
—
головними центральними осями
і
осі
симетрії.
3. Переріз має дві осі симетрії
і
моменти інерції відносно них рівні
—
псі
центральні
осі є
головними
і
моменти інерції відносно них рівні.
4. Переріз
має
більше
двох
осей симетрії (круг, кругове кільце,
правильні
многокутники) —- довільна центральна вісь
є
головною.
Всі
головні центральні моменти такого перерізу рівні між собою.
Поняття
про інші ГХ перерізу дано
у
відповідних розділах.
53

Розділ
З
3.1.7. ВИЗНАЧЕННЯ ПОЛОЖЕННЯ
ГОЛОВНИХ
ЦЕНТРАЛЬНИХ
ОСЕЙ
І ВЕЛИЧИНИ
ГОЛОВНИХ
ЦЕНТРАЛЬНИХ
МОМЕНТІВ ІНЕРЦІЇ
Порядок
розрахунку,
1. Викреслюють переріз у масштабі.
2. Розбивають переріз на прості частини, ГХ яких відносно власних
центральних осей легко визначити або вони відомі. Проводять для кожної
частини прямокутну систему центральних осей х., у
с
Додатний напрямок
паралельних осей
усіх
частин однаковий. Обчислюють ГХ перерізів
простих частин відносно власних центральних осей. ГХ перерізів профіль-
ного прокату беруть з таблиць сортаменту. Для простих геометричних
фігур можна скористатись таблицею 3.1 посібника.
3. Проводять довільну систему прямокутних осей і за формулами
(3.4) визначають центр ваги перерізу. Візуальна перевірка правильності
визначення
центра ваги: а) при
двох
простих частинах він знаходиться на
відрізку, що з'єднує центри ваги простих перерізів; б) при наявності більше
двох
простих частин він знаходиться в межах площі, обмеженої відрізками,
що сполучають центри ваги простих частин.
4. Проводять початкову систему центральних осей х
с
, у
с
, паралельних
осям
x
t
, у.. В системі осей х
с
, г/
с
визначають координати центрів ваги
простих частин. Виконують остаточну перевірку правильності знаходження
центра ваги: статичні моменти перерізу відносно центральних осей х
с
, у
с
повинні
дорівнювати нулю.
5. За формулами (3.9)—(3.11) визначають осьові (J
Is
, /
А
) і відцентровий
/щ,
(
моменти інерції всього перерізу відносно початкових центральних осей.
6. За формулами
(3.14)
і
(3.15)
визначають положення головних цент-
ральних осей х, у і величину головних центральних моментів інерції /., / .
7. Виконують перевірку правильності обчислень. Для цього переві-
ряють постійність суми
^+4
=/,+./,=
const.
(3.16)
а також знаходять за формулою повороту осей
(3.13)
значення відцентро-
вого моменту інерції J
r
відносно головних осей х, у. Зрозуміло, що значення
повинно
наближатись до нуля (різниця складає похибку обчислень):
ГЕОМЕТРИЧНІ ХАРАКТЕРИСТИКИ ПЕРЕРІЗІВ
(3.17)
54
Таблиця
3.1
У
с
ь
-т—
^
Прямокутник
А
= bh;
12
/ = .
12
-4 =
Круг
nd
1
X ,4
J.-J =^-
' ' 64 •
32
Напівкруг
mt'
Л =
' =
O.OO686rf'
L =
126
Паралелограм
Ук
Трикутник
(прямокутний
" 36
36
Кругове кільце
4
Еліпс
A
= nab
nab
3
4
Трикутник
55

Розділ
З
3.2.
ПРАКТИЧНІ
ЗАНЯТТЯ
3.2.1.
КОНТРОЛЬНІ
ЗАПИТАННЯ
1. Навіщо потрібні геометричні характеристики перерізів?
2. Що таке статичний момент? Як він обчислюється і які значення
може приймати?
3. Як обчислюють статичний момент складного перерізу?
4. Де використовують ггоняття статичного моменту?
5. Які моменти інерції ви знаєте?
6. Яка залежність між полярним і осьовими моментами інерції?
(Полюс
— в початку координат).
7. Які значення може приймати відцентровий момент інерції?
8. Яка залежність між моментами інерції відносно паралельних осей,
одні з яких — центральні?
9. Як обчислюють моменти інерції складних перерізів?
10. Як змінюються моменти інерції при повороті координатних осей?
11.
Які осі називаються головними і як визначають ЇХ положення?
12. Що таке головні моменти інерції і як їх визначають?
13.
Що таке головні центральні осі і головні центральні моменти інерції?
14. Які ви знаєте часткові випадки визначення положення головних
центральних осей?
. 15. Записати формули моментів інерції для простих перерізів (прямо-
кутного, трикутного, круглого, кругового кільця).
16. Як визначають геометричні характеристики прокатних профілів?
17. В яких одиницях вимірюють статичні моменти і моменти інерції?
3.2.2.
ПРИКЛАДИ
ОБЧИСЛЕННЯ
МОМЕНТІВ
ІНЕРЦІЇ ПЕРЕРІЗІВ
Приклад 3.1.
Обчислити площу
і
головні центральні моменти перерізу
(рис.
3.5). Як
зміняться площа
і
моменти інерції при відсутності отворів? Прийняти
Ь
= 9 CM, h = 16 см, d = 5 см, а = 4 см.
Розв'язання.
Переріз можна представити
як
складну плоску фігуру,
що
складається
з
трьох простих частин: прямокутника
bxh і
двох кругів діаметром
d
«від'ємної* площі.
56
ГЕОМЕТРИЧНІ ХАРАКТЕРИСТИКИ ПЕРЕРІЗІВ
Площа
Л = Д-2Л - 6 •
А
- 2
тій
2
/4
= 16 - 9 - ге • 5^/2 = 104,7 см
1
.
J
s
, 1 —
головні центральні моменти інерції, тому
що осі х, у є
головними
центральними
як осі
симетрії.
Обчислюємо власні моменти інерції простих частин. Згідно
з
табл.
3.1:
— для
прямокутника
11
12 12
• '" 12 12
— для
круга
I'l
=l'l=n-
d*/64
- к - 5
4
/б4 =
ЗО,
7 см\
За
формулами
(3,9)
обчислюємо моменти інерції частин відносно осей
х і у.
Ґ
х
= l'
h
=
3072
см* (осі х і х
х
збігаються):
І"
=
J
i +
а
Ч = 30,7 + 4
г
• л • 5
2
/4 -
344,9
си«;
У
г
'
=І'
Я
=$72
CM*;
J" =/,"
=30,7
С
ж
1
(осі
у, у, і
^збігаються).
За
формулами (3.11) обчислюємо головні центральні моменти інерції:
/, = 5[ - 2J'J =
3072
- 2 •
344,9
-
2382,2
см*;
l,=K-
2I
> =972-2-30,7
= 910.6 см*.
При
відсутності отворів площа збільшиться
на
1
І1І1^І.100%
=
37
1
5%;
Рис.
3.6
57
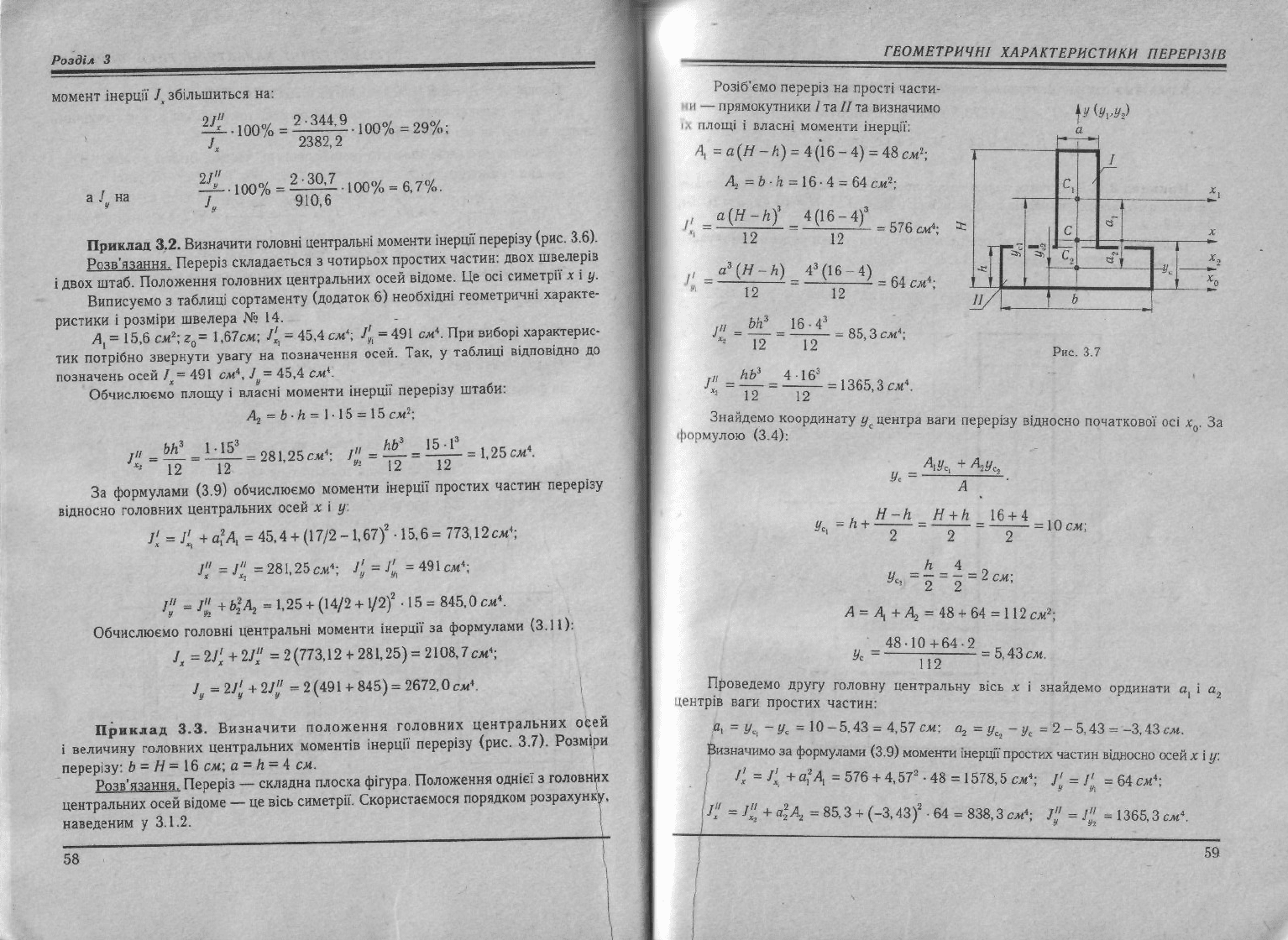
Розділ
З
момент інерції ^збільшиться на:
а/
у
на
VL.
100%
=
910,6
.
100% = 6,7%.
Приклад
3.2. Визначити головні центральні моменти інерції перерізу (рис. 3.6).
Розв'язання,
Переріз складається з чотирьох простих частин:
двох
швелерів
і
двох
штаб. Положення головних центральних осей відоме. Це осі симетрії х і у.
Виписуємо з таблиці сортаменту (додаток 6) необхідні геометричні характе-
ристики
і розміри швелера № 14.
А,
~ 15,6
CM
2
;
z
o
=
1,67СЛІ;
/
Г]
= 45,4 см*; J
gl
~ 491 см*. При виборі характерис-
тик
потрібно звернути
увагу
на позначення осей. Так, у таблиці відповідно до
позначень
осей / = 491
CM
4
,
J = 45.4 см
А
.
Обчислюємо площу і власні моменти інерції перерізу штаби:
"-
12
12 12 "- 12 12
За
формулами (3.9) обчислюємо моменти інерції простих частин перерізу
відносно головних центральних осей х і у:
3[ = І\ + of Д = 45,4 + (17/2 -
1,67)
г
-15.6 = 773,12 см
4
;
',"
= ^ + N4 =1.25 + (14/2 + !/2)
2
•
15 =
845.0
см\
Обчислюємо головні центральні моменти інерції за формулами (3.1!):
У,
=2Ґ,+2Ґ,'
=2(773.12 +
281,25)
=
21О8,7сж*;
I
t
= 1l[ + 2J'J - 2 (491 + 845) =
2672,0
см\ \
Приклад
3.3. Визначити положення головних центральних осей
і
величину головних центральних моментів інерції перерізу (рис. 3.7). Розміри
перерізу: b = Н = 16
CM;
a = h
—
4 см.
різу:
b Н ;
Розв'язання.
Переріз — складна плоска фігура. Положення однієї з головних
центральних осей відоме — це вісь симетрії. Скористаємося порядком розрахунку,
наведеним у
3.1.2.
ГЕОМЕТРИЧНІ ХАРАКТЕРИСТИКИ ПЕРЕРІЗІВ
Розіб'ємо
переріз на прості части-
н
— прямокутники /та //та визначимо
.
площі і власні моменти інерції:
Л,
= а (Я - h) = 4 (16 - 4) = 48
см>;
А
г
=Ь-к = 16-4 =
64t«
3
;
/•
=.
Ч-h'f 4(16-4)*
(H~k)
12
12
,„
hb
3
4-16
3
12
•
= 64 см";
Рис.
3.7
її =
12
12
=
1365, Зе
Знайдемо
координату у. центра ваги перерізу відносно початкової осі х
0
. За
ормулою (3.4):
А
H + h 16 + 4
=
Д + А; =48 + 64 =
48 .10+ 64-2
112
=
5,43
см.
Проведемо
другу
головну центральну вісь х і знайдемо ординати о, і а
2
центрів ваги простих частин:
ft =У
Ч
-(/
с
=10-5,43=
4,57 сл; а
2
= у
ч
- у
с
= 2 -5,43 =
-3,43СЛІ.
Визначимо за формулами (3.9) моменти інерції простих частин відносно осей х і у:
і
К =К, +"М = 576+
4,57
а
-48
=
1578,5
сж
4
; /
(
' = 1^ =
64с«
4
;
*
4
:
К' =J'J =
1365,3
ел
4
.
59
