Колпаков В.М. Теория и практика принятия управленческих решений

Подождите немного. Документ загружается.

условий (данные из примера 4) с поправкой на коэффициент ве

роятности каждого условия. Полученные значения суммируют.

Максимальная прибыль при низком спросе — 8, среднем — 10, вы

соком — 14. Следовательно, ожидаемая прибыль в условиях уве

ренности

0,4 (8) + 0,6 (10) + 0,3 (14) = 13,4.

2. Ожидаемая прибыль в условиях риска (для примера 4) равна

11,4, следовательно, ПСТИ = 13,4 — 11,4 = 2. Эта цифра характери

зует верхнюю границу суммы, которую лицо, принимающее реше

ние, планирует израсходовать на получение информации. Если зат

раты равны этой сумме или превышают ее, то следует придерживать

ся альтернативы с максимальной ожидаемой прибылью и не расхо

довать дополнительные средства.

Пример 7. Определить ожидаемую стоимость точной информа

ции, необходимой для планирования производственных мощностей,

относительно убытков от упущенных возможностей.

Решение. Используя данные примеров 2 — 4, рассчитывают ожи

даемые убытки для каждого варианта.

Мощность:

малая — 0,4 (0) + 0,6 (2) + 0,3 (6) = 3;

средняя — 0,4 (2) + 0,6 (0) + 0,3 (4) = 2 (минимум);

высокая — 0,4 (5) + 0,6 (8) + 0,3 (0) = 6,8.

Возможный наименьший убыток равен 2, что соответствует ре

зультату примера 6, где используется другой подход.

Анализ чувствительности [131]. Состоит в определении такого

уровня вероятности, для которого альтернатива имеет максималь

ную предполагаемую прибыль. Анализ позволяет оценить чувстви

тельность показателей вероятности. Определяется уровень вероят

ности, после которого выбор варианта не меняется.

Пример 8. Используя данные табл. 3.10, определить уровень веро

ятности Р(2) для условия 2, где каждая альтернатива относительна,

при использовании подхода ожидаемой стоимости.

Решение. На графике строят все альтернативные варианты, свя

занные с Р(2). На рис. 3.1 с левой стороны обозначены показатели 1,

а с правой — показатели 2. Например, для варианта А отмечают сле

ва точку 4, а справа — 12, и точки соединяют прямой. Штриховой

231

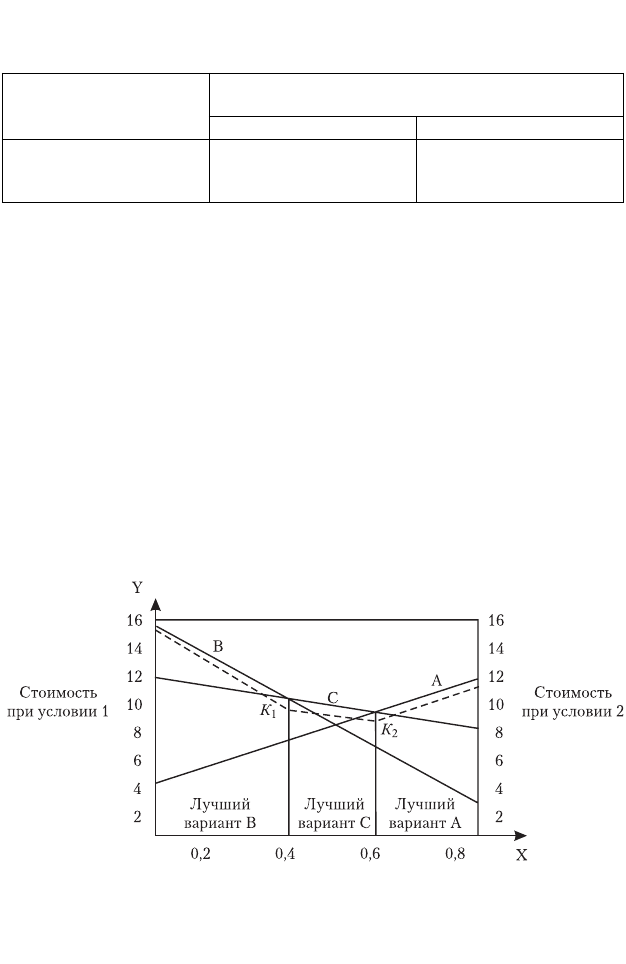
линией показаны оптимальные значения Р(2), выше которых каж

дая альтернатива оптимальна.

Следует обратить внимание, что в точках пересечения две альтер

нативы, показанные линиями, будут эквивалентны с позиции ожи

даемой стоимости. Для определения точек пересечения необходимо

получить уравнение каждой кривой. Уравнения имеют вид y = a + bx,

где а — точка пересечения с осью Y cлева, b — угол наклона x — P(2).

Наклон определяется как изменениe величины Y при изменении Х

на единицу. В данном типе задач расстояние между двумя вертикаль

ными осями равно 1. Следовательно, наклон всех прямых равен пра

вому значению минус левое значение (табл. 3.11).

Из рис. 3.1 видно, что альтернатива В оптимальна от Р(2) = 0 до

точки К

. От точки К

до К

лучше вариант С.

232

Альтернатива

Ожидаемая стоимость при возможном условии,

млн грн.

Вариант 1 Вариант 2

Таблица 3.10

Исходные данные

Рис. 3.1. График анализа чувствительности

Решая уравнение 16 — 14 Р(2) = 12 — 4 Р(2), получают значе

ние точки К

= 0,40. Для нахождения точки К

решают уравнение

4+ 8 Р(2) = 12 — 4 Р(2); Р(2) = 0,67. Найдя К

и К

, можно утверж

дать, что альтернатива С будет точнее в интервале от Р(2) > 0,4 до

Р(2) = 0,67. При необходимости решить проблему относительно

Р(1) следует определить (аналогично рассчитанному Р(2)) и вы

честь каждое значение Р(2) из 1,0.

Основы прогнозирования

Наиболее используемые при производстве товаров и оказании

услуг прогнозы основаны:

• на суждении и мнении;

• на данных временного ряда;

• на ассоциативных методах прогнозирования.

При прогнозировании стараются применять упрощенные вари

анты методов, что характерно для малого бизнеса.

Прогнозы, основанные на суждении и мнении. Эти прогнозы ос

нованы на анализе субъективных данных, полученных при опросе

потребителей, сотрудников отдела продажи, линейных менеджеров,

групп экспертов.

Опросы потребителей. Потребители — это люди, которые опре

деляют спрос. Зная их мнение и потребности, можно спланировать

производство. Однако при всей его простоте это достаточно сложный

метод. Проводя опросы, следует учитывать психологию потребителей

при покупке товаров. Так, мнение будущего покупателя определяется:

• ситуацией, когда восприятие, память человека подвержены влия

нию когнитивных (внутренних, субъективных) и мотивационных

факторов, что приводит к предвзятости в суждениях;

233

Альтернатива

Возможное условие

Угол наклона Уравнение

Вариант 1 Вариант 2

12—4 = 8

2—16 = —14

8—12 = —4

4 + 8 Р(2)

16—14 Р(2)

12—4 Р(2)

Таблица 3.11

Исходные данные и решения

• тем, как и кем задан вопрос (в каком свете он сформулирован, ка

ков контекст, содержит ли он уловки и т. п.);

• социальным окружением лица, высказывающего суждение;

• эвристическими способностями и субъективным смещением

мнения и т. п.

Зная особенности психики человека, можно более обоснованно

интерпретировать ответы потребителей. Это требует знаний и навы

ков. Опросы могут потребовать финансовых расходов и времени, но

позволяют извлекать информацию, которую нельзя получить из

других источников.

Опросы сотрудников отдела продажи могут служить источни

ком очень ценной информации для прогноза, поскольку это, как пра

вило, специалисты, непосредственно контактирующие с потребите

лями. Однако здесь следует учитывать инерцию мышления, наличие

прошлого опыта у продавца товара. Так, прошедший период успеш

ных продаж он может воспринимать как тенденцию.

Мнение руководства достаточно ценно в силу обобщенности ин

формации из различных каналов. Необходимо учитывать влияние

лидера на коллективное мнение.

Группы экспертов используются для составления прогноза или

создания нескольких его вариантов и последующего отбора наибо

лее подходящего. В данном случае может быть полезен метод Дель

фи. Для участия в опросе могут привлекаться менеджеры и сотруд

ники компании анкетирования. Благодаря этому создается согласо

ванный прогноз с наименьшими затратами.

Прогнозы, основанные на данных временного ряда. Под вре

менным рядом понимают упорядоченную во времени последова

тельность наблюдений через разные промежутки времени (через

1 час, ежедневно, ежегодно). Данными могут быть показатели спро

са, дохода, прибыли, отгрузок, несчастных случаев, производитель

ности и т. п. Прогноз основан на анализе данных временного ряда.

Предполагается, что будущие значения ряда могут быть оценены ис

ходя из прошлых. В данном случае фиксируется и строится тенден

ция проявления какихто фактов. Если эти проявления были резуль

татом действия объективных закономерностей в прошлом, то в по

добных условиях в будущем они повторятся. На практике требуется

фиксировать показатели, представляющие интерес, через заданное

время и строить график, где на оси Х отмечают значение показателя,

234

а на оси Т — время. На графике могут проявляться одна или несколь

ко закономерностей: тенденция, сезонные изменения, циклы и пос

тоянные изменения (вокруг некоторого среднего значения) [131], а

также случайные или нерегулярные изменения. Выбирая параметр

временного ряда, следует учитывать объективность его фиксации.

Например, если требуется изучить спрос на какойто продукт в

прошлом году, то параметром, изменения которого позволят разра

ботать прогноз, должен быть не спрос, а объем продаж.

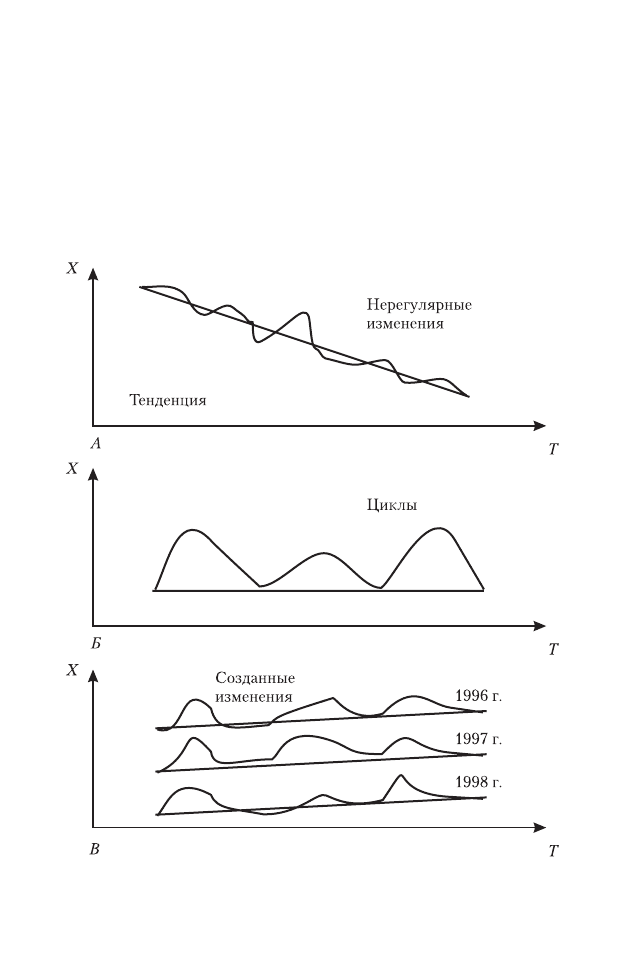
На рис. 3.2 показаны тенденции, сезонные изменения, циклы,

случайные и нерегулярные изменения.

235

Рис. 3.2. График изменений циклов:

А — сезонных, Б — случайных, В — нерегулярных

Методы усреднения. Фиксируемые данные о какомлибо явлении

часто содержат “выпадающие” из общей тенденции значения показате

ля. Следствием этого может быть влияние существенных и несущест

венных факторов. На практике, определяя общую тенденцию, ими

обычно пренебрегают, усредняя значения показателя. К прогнозам,

составленным методом усреднения, относятся прогнозы “наивные”,

скользящие средние значения, экспоненциального сглаживания [131].

“Наивным” является прогноз на данный период, который равен

фактическому значению предыдущего прогноза. Так, если сегодня

спрос на продукцию составляет 40 т, то и через неделю спрос не из

менится. Этот прогноз можно успешно использовать, когда выявле

на закономерность (тенденция, сезонность и т. п.).

Скользящее среднее значение — прогноз, построенный на основе

усреднения нескольких последних показателей. Прогноз (ПГ) мож

но определить так:

где i — “возраст” данных, i = 1, 2, 3, … ; n — количество периодов в

скользящем среднем значении; A

— текущие значения.

Пример 9. Вычислить скользящее среднее значение за три перио

да на основе показателей спроса на продукцию фирмы за последние

пять периодов:

Период “Возраст” данных Спрос на продукцию, усл. ед.

15 52

24 50

33 53

42 50

51 51

Решение. Рассчитывают значение прогноза:

Если фактический спрос в течение периода 6 оказывается 49, то

прогноз скользящего среднего значения для периода 7 составит

53 51 50

ПГ 51,3.

ПГ ,

∑

236

Прогноз модифицируется при поступлении каждого нового фак

тического значения показателя спроса прибавлением его и вычита

нием прежнего с последующим вычислением среднего. Прогноз как

бы “скользит”, отражая только последние значения. Скользящее

среднее значение может включать необходимое количество перио

дов. При этом следует иметь в виду, что число усредненных точек на

графике характеризует чувствительность для каждого нового значе

ния. Среднее значение более чувствительно к усреднению меньшего

числа показателей. Следовательно, разрабатывая этот прогноз, необ

ходимо выбирать между высокой чувствительностью к случайным

изменениям данных и медленной реакцией на изменения. Недоста

ток этого прогноза состоит в том, что все значения учитываются как

среднее (равнозначное) без значимости (веса) показателя.

Взвешенное среднее подобно скользящему среднему значению, но

придает больший вес (коэффициент значимости) последним показа

телям временного ряда.

Пример 10. По показателям спроса необходимо:

1) рассчитать прогноз для взвешенного среднего значения, когда

последнему значению присвоен коэффициент значимости 0,50,

предшествующим — 0,20; 0,22 и первому — 0,08;

2) определить прогноз спроса для периода 7, если фактический

спрос для периода 6 равен 49.

Период Спрос на продукцию, усл. ед.

152

250

353

450

551

Решение:

1. ПГ = 0,50 (51) + 0,20 (50) + 0,22 (53) + 0,08 (50) = 47;

2. ПГ = 0,50 (49) + 0,20 (51) + 0,22 (50) + 0,08 (53) = 50.

При использовании четырех коэффициентов значимости берут

четыре последних значения. Однако следует учесть, что коэффици

ент значимости устанавливается экспериментально.

50 51 49

ПГ 50.

237

Экспоненциальное сглаживание достигается, когда каждый новый

прогноз основан на предыдущем с прибавлением (суммированием)

процента разности между этим прогнозом и фактическим значением

ряда в данной точке:

Очередной прогноз = (предыдущий прогноз) + a(фактический

прогноз – предыдущий прогноз), где a — процент разности; (факти

ческий прогноз — предыдущий прогноз) — погрешность прогноза, или

= F

t–1

+ a(A

t–1

– F

t–1

где F

, F

t–1

— прогноз для периода соответственно t и t–1; a — сгла

живающая константа; A

t–1

— фактический спрос.

Пример 11. Вычислить прогноз. Согласно предыдущему прогнозу бы

ло реализовано 52 усл. ед. Фактический прогноз равен 50 усл.ед.; a = 0,10.

Решение.

1. Новый прогноз определяют следующим образом:

= 52 + 0,10 (50 – 52) = 52,2.

2. Если фактический спрос стал равен 53 усл. ед., то согласно сле

дующему прогнозу

= 52,2 + 0,10 (53 – 52,2) = 52,28.

Прогнозирование по выявлению тенденции. Анализ тенденций

используется для построения уравнения, выражающего характер из

менений параметров в виде математических зависимостей. Выяв

ленные математические зависимости тенденций позволяют прогно

зировать с использованием математического аппарата. Наиболее

распространены на практике два способа разработки прогнозов при

выявленной тенденции: использование уравнения тенденции и рас

ширение экспоненциального сглаживания.

Наиболее простым уравнением тенденции является линейное:

= a + bt ,

где Y

— прогноз для периода t; a — значение Y

при t = 0; b — нак

лон линии; t — количество прогнозов.

238

Например, при уравнении Y

= 50 + 5t имеем линейную тенден

цию. Экспоненциальное сглаживание тенденций является разно

видностью экспоненциального сглаживания, используемого при t = 0,

= 50 и наклоне линии, равном 5. Следовательно, в среднем Y

уве

личивается на 5 ед. для каждого единичного увеличения t при выяв

лении тенденции. Прогноз, скорректированный тенденцией, состоит

в выявлении сглаженной ошибки и фактора тенденции:

ПГ

t + 1

= S

+ T

где S

— сглаженный прогноз; S

= ПГ

t+1

+ a

– ПГ

); T

— оценка

текущей тенденции; T

= T

t –1

+ a

(ПГ

– ПГ

t–1

– T

t–1

); а

, a

— сгла

живающие константы.

Для использования метода необходимо выбрать значения a

и a

(обычным подбором), сделать начальный прогноз и оценку тенденции.

Рассмотрим уравнение экспоненциального сглаживания тенден

ций на примере [131].

Пример 12. По показателям уровней продаж за последние 10 недель:

1) определить уравнение линии тенденции;

2) спрогнозировать уровень продаж в последующие две недели

(периоды t = 11 и t =12).

Неделя 1я 2я 3я 4я 5я 6я 7я 8я 9я 10я

Уровень продаж,

усл. ед. 700 724 720 728 740 742 758 750 770 775

Решение.

1. Из исходных данных видно, что с каждой неделей увеличи

ваются продажи по линейной функции (график можно не строить).

2. Определяют наклон линии b:

где n — количество периодов; y — значение временного ряда; t — пе

риод времени;

;

nybt

−

∑∑

()

nty t y

nt t

−

∑∑∑

∑∑

239

Из полученных результатов следует, что линия тенденции

= 699,40 + 7,51t,

где t = 0 для нулевого периода.

3. Определяют прогнозы для будущих периодов (t = 11; t = 12):

= 699,40 + 7,51 (11) = 782,01;

= 699,40 + 7,51 (12) = 789,51.

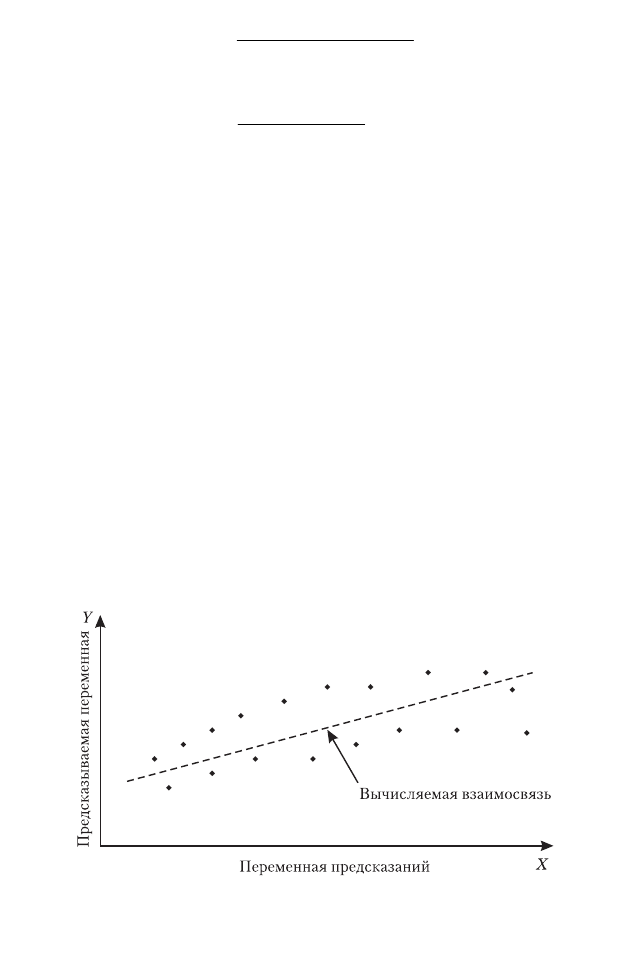
Регрессионный анализ. Простая линейная регрессия [131].

Простая наиболее распространенная форма регрессии представляет

собой линейную связь между двумя переменными (рис. 3.3). Цель

линейной регрессии — получить уравнение прямой линии, которая

дает минимальную сумму квадратов вертикальных отклонений то

чек данных от линии.

10 41 358 55 7407

7,51;

10 385 55 55

7407 7,51 55

699,40.

⋅−⋅

−⋅

240

Рис. 3.3. Регрессионный анализ (простая линейная регрессия)