Киреев П.С. Физика полупроводников

Подождите немного. Документ загружается.

Исходя из его размерности, назовем его тензором эффективной

iaccbi. Его компоненты m

не равны обратным величинам компо-

нентов тензора обратной эффективной массы, т. е.

(

dPidPj

Они должны находиться из условия

*-i __

*-i

* = I,

(12.22)

где I есть единичный тензор. Рассмотрим частный случай, когда

тензор т*"

имеет диагональный вид

{т

}

= т?6

(12.23)

Обозначим компоненты тензора т* в виде m

iJ%

Так как

1 при

О при IΦ /,

'/у

= δ

ί7

= {

(12.24)

то на основании правил умножения матриц из (12.22) запишем,

учитывая (12.24):

2 т

{m*-i}

= 2 ттТЬи =

тт

= Ь

. (12.25)

Мы видим, что

= ^ Ьц = mjbij, (12.26)

т. е. если т*

-1

является^ёиаёональным тензором, то тензор т

также является диагональным, причем по диагонали его стоят эле-

менты, обратные элементам тензора

обратной эффективной массы.

Запишем это подробно. Если обозначим

mji = д

Е (dPf) = mj

то тензоры т* и ш*

-1

будут иметь вид

т**

— О О

0 — 0

оо—з

(т

0 0

т* =

(

0 т

0 0 т

(12.27)

(12.28)

В дальнейшем величины т,· будем называть компонентами эффек-

тивной массы, а деление на гп* будем понимать как умножение

на т*-

(и наоборот).

Изоэнергетическая поверхность описывается уравнением

E<JP)=E

{

-Ρ , (

х-

охУ* . (Ру-Роу)* , 1Р.-Р0.Г

2m,

2 m

2 rrio

= const. (12.29)

Если ввести полуоси эллипсоида а, Ь, с и записать уравнение

эллипсоида в канонической форме

(fir-Яе,)» , (Ру-РоуУ* , Рм-РомУ* .

/100Л

* + Ρ + *

^ (

)

то легко видеть, что длина полуосей пропорциональна корню квад-

ратному из соответствующих величин тс.

(Е-

) т

\ Ь

= 2(Е -Е

)

; с

(Е-

)

щ. (12.31)

Рассмотрим случай, когда все три элемента эффективной массы

равны: m

= m

В этом случае тензор эффективной массы вырождается в скаляр

(тензор нулевого ранга), и изоэнергетические поверхности представ-

ляют собой сферы:

* £ = + = const. (12.32)

Если равны какие-либо два элемента тензора, например т

= т

Φ m

то

Е =Е

° + 2т

+ 2т

C0Ilst

(

и изоэнергетические поверхности представляют собой эллипсоиды

вращения вокруг оси P

. Если т

<С.т

3у

то .эллипсоид вращения

будет вытянут вдоль оси вращения, причем он вытянут тем больше,

чем больше отношение эффективных масс т

/т

. Если m

то

эллипсоид сжат вдоль оси вращения.

В общем случае различных эффективных масс m

эллипсоид

имеет три различных полуоси. При этом необходимо помнить, что

чем сильнее различаются величины эффективных масс т

тем сильнее «вытянут» эллипсоид.

С ростом разности энергии £(к)

—

необходимо учитывать

последующие члены ряда Тейлора; эллипсоиды энергии будут дефор-

мироваться, превращаясь в более сложные поверхности энергии.

§ 13. СВЯЗЬ СКОРОСТИ С КВАЗИИМПУЛЬСОМ

бок Пуассона

Оператор скорости ν определяется с помощью квантовых ско- j

\ = dr/dt = [Η, r] = ^(rH-Hr), · (13.1)

гд е г —оператор координаты и

—оператор Гамильтона. Для вычи-

сления коммутатора г и Η удобно перейти к Е- или к-представле^-

нию, когда все операторы задаются в виде определенных действий

над переменной к, от которой могут зависеть функции. Оператор

Гамильтона в к- или Ε-представлении есть оператор умножения,

или просто энергия Ε (к):

Н(к) = £(к). (13.2)

Чтобы найти вид оператора г (к), учтем, что if>

(r) тесно связана

с собственной функцией оператора г (к), которую обозначим через ψ

(к):

Γ(κ)ψ

(κ) = ήΜκ), (13.3)

где г есть собственное значение оператора координаты, (к) его

собственная функция, заданная в к-представлении.

Как известно из квантовой механики, собственные функции двух

операторов во взаимных представлениях связаны простым соотно-

шением: если собственная функция L в Λί-представлении есть (Μ)

ИМ)ЫМ) = /лЫМ), (13.4)

а собственная функция Μ в L-представлении есть ψ^ι (£)

M(L)^(L) = M^(L), (13.5)

то

ЫМ) = г№(1). (13.6)

На основании этого можно записать собственную функцию опе-

ратора г (к) в к-представлении в виде:

(к) = φ* (г) =ег^г)ц*

(г)

, (13.7)

после чего легко найти вид оператора г (к) на основании уравнения

на собственные функции и собственные значения:

^φρτ^)==Γψ

(κ), (13.8)

или

г>)г|>*(г) = п|>*(г). (13.9)

Смысл этого соотношения состоит в том, что нужно подобрать

такую форму оператора г (к), чтобы после его воздействия на функ-

цию г|?к(г) получить ту же функцию, умноженную на г. При этом

необходимо действовать на ψκ (г) только по переменной к.

Рассмотрим действие оператора d/(dk) = V

на функцию ψκ (г):

(г) = V

[е-^

кг

>фк (г)] = -

/п|>*

(г) + e-'<

(p* (г) =

= - /πψ* (г) + (г) [V

1η

φ* (г)], (13.10)

или

ψ* (г) = [iV

- (iV

1η

φ5)] ψ* (г) =

(к) ψ

(г), (13.11)

т. е. оператор

(κ)

= /ν

-ί(ν

1ηφ*) (13.12)

представляется в виде суммы операторов дифференцирования по

волновому вектору (или квазиимпульсу) и умножения на некоторую

функцию от к (и г). Вместо члена

—

i (V

1η

cpt)

можно ввести

неко-

торый оператор Ω, разложив функции ν

φ* по функциям φ

При U(г) = const второй член обращается в нуль, и г(к) имеет

обычный вид оператора координаты в р-представлении, поскольку

в этом случае квазиимпульс тождествен импульсу. Теперь можно

записать выражение для оператор а. скорости в к-представлении:

ν (к) = 1

{г

(к) Ε (к) - Ε (к) ? (к)} = 1 , (13.13)

который имеет вид оператора умножения на производную энергии

по квазиимпульсу:

ν(κ)4^ = §

ν(Ρ) = ν. (13.14)

Это соотношение подобно выражению для групповой скорости

волнового пакета

= dE/dp. (13.15)

Средняя скорость электрона в состоянии с энергией Ε (к) (с вол-

новой функцией г|)

(г), но не ψ£(

)) имеет вполне определенное зна-

/ч 1 dE dE

чение, зависящее от этого состояния и равное (v) = v=.y j- = ^р

(опустим знак < )). (13.16)

Таким образом, усредненная по состоянию с определенной энер-

гией (точнее: и по бесконечно малому интервалу энергий) скорость

электрона определяется в виде производной энергии по квазиимпульсу.

В точках экстремума средняя в квантовомеханическом смысле ско-

рость равна нулю. (В дальнейшем слова «средняя в квантовомеха-

ническом смысле» будем опускать.)

Если рассматривать состояния в малой окрестности экстремаль-

ных точек, где энергия имеет квадратичную зависимость от квази-

импульса:

2 (13.17)

то

ι-J. <

ΐ3

·'

или в векторной форме

v==

i^(

»)' <

,9)

т. е. в общем случае скорость равна скалярному произведению кв

зиимпульса на тензор обратной эффективной массы. Если тензор

ш*"

имеет диагональный вид

{т*->Ь

= тГб,

, (13.20)

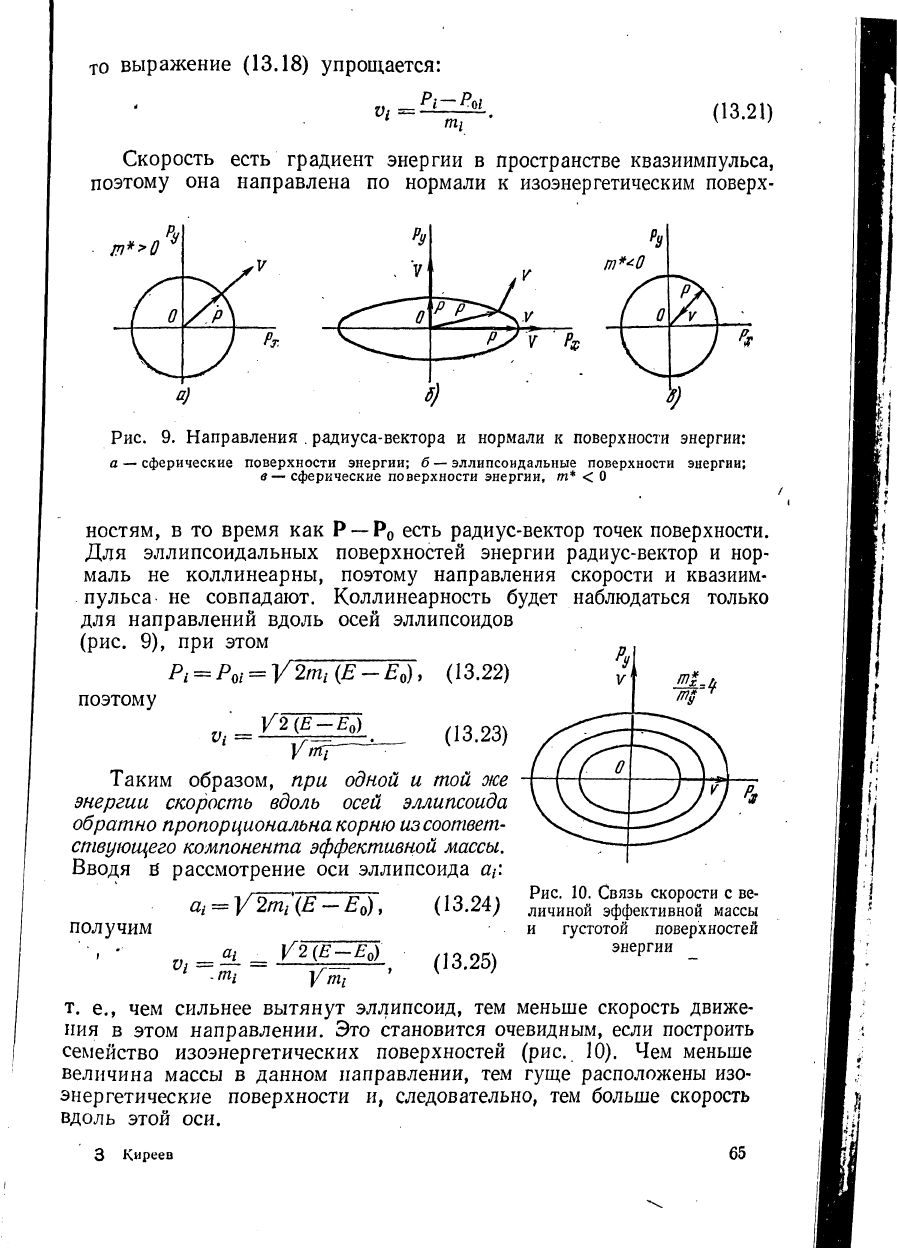
то выражение (13.18) упрощается:

(13.21)

Скорость есть градиент энергии в пространстве квазиимпульса,

поэтому она направлена по нормали к изоэнергетическим поверх-

(

• " . F'

ЛР\ 0

У т**0

i£>V С о

2ν·

)

Рт

J *

а)

Рис. 9. Направления . радиуса-вектор а и нормали к поверхности энергии:

а — сферические поверхности энергии; б — эллипсоидальные поверхности энергии;

в — сферические поверхности энергии, т* < О

ностям, в то время как Р — Р

есть радиус-вектор точек поверхности.

Для эллипсоидальных поверхностей энергии радиус-вектор и нор-

маль не коллинеарны, поэтому направления скорости и квазиим-

пульса не совпадают. Коллинеарность будет наблюдаться только

для направлений вдоль осей эллипсоидов

(рис. 9), при этом

= P

= Y2m

{E-E

), (13.22)

поэтому

V2 (Е-Ε о)

Vrrqr

(13.23)

Таким образом, при одной и той же

энергии скорость вдоль осей эллипсоида

обратно пропорциональна корню из соответ-

ствующего компонента эффективной массы.

Вводя в' рассмотрение оси эллипсоида

(13.24)

(13.25)

ρ»

if f Ί

получим

Οι

= у

2/72/

(Ε

—

\f2 (Е-Е

)

αϊ

Рис. 10. Связь скорости с ве-

личиной эффективной массы

и густотой поверхностей

энергии

Vtm

т. е., чем сильнее вытянут эллипсоид, тем меньше скорость движе-

ния в этом направлении. Это становится очевидным, если построить

семейство изоэнергетических поверхностей (рис. 10). Чем меньше

величина массы в данном направлении, тем гуще расположены изо-

энергетические поверхности и, следовательно, тем больше скорость

вдоль этой оси.

3 Киреев

Необходимо остановиться на одном существенном моменте, свя-

занном со знаком эффективной массы. Предположим для простоты,

что эффективная масса —скалярная величина. В этом случае век-

торы ν и .(Р

—

) коллинеарные, однако их направления зависят

от вида экстремума. Для минимума ш*>0 и скорость ν совпадает

по направлению с (Р —Р

). Для максимума энергии т* < 0 и ско-

рость направлена против (Р —Р

) (см. рис. 9, в).

§ 14. ОПЕРАТОР УСКОРЕНИЯ

Оператор ускорения а определяется как производная от опера-

тора скорости по времени:

a=.dv/d/ = [H, v] = i(vH-Hv). (14.1)

Легко видеть, что а = 0 при движении электрона в периодическом

поле решетки. Действительно, в к-представлении Н(к)н=£(к) и

ν (к) = dE (к)/Н άκ, поэтому

ν Η

—

Hv = 0. (14.2)

Но так как коммутатор двух операторов не зависит от вида

представления, то а^О и

(а) = (а) = 0. (14.3)

Это значит, что электрон движется в периодическом поле без

ускорения. Интуитивное представление о движении электрона как

о периодически повторяющемся ускорении и замедлении лишено

основания.. Причиной этого является наличие (наряду с корпуску-

лярными) волновых свойств у электрона. Это приводит к тому, что

его средняя скорость является интегралом движения, подобно тому,

как сохраняется скорость свободно движущейся частицы.

Напомним, что одновременно с этим сохраняются во времени энер-

гия и квазиимпульс. Импульс же частицы периодически меняется:

dp/dt = — Vi/(r) = F

, (14.4)

так как сила F

·, действующая на электрон со стороны решетки,

имее т период решетки

F; (Г+ 11)^(11). (14.5)

Пусть теперь на кристалл наложено некоторое «внешнее» поле

с потенциальной энергией 1/(г).

В этом случае, как мы знаем, квазиимпульс начинает изменяться

dP/dt = F

= -VV(r), ' (14.6)

если V (г + п) ^ V (г), т. е. поле не является периодическим. Ква-

зиимпульс меняется под действием внешней силы F

, обусловленной

любым нарушением периодического поля. Точка в к-(или Р)-прост-

ранстве, изображающая состояние, начинает перемещаться в соот-

ветствии с уравнением

dP/dt = F

. (14.7)

Из (14.7) можем записать

P(0 = P

+S Fa (ξ) dt (14.8)

Если внешняя сила не зависит от времени, то

P(t) = P

+ FJ. (14.9)

Траекторией частицы в Р-пространстве является прямая линия, зада-

ваемая направлением внешней силы F

. Но если частица начинает

двигаться в пространстве квазиимпульса, то она переходит от одной

поверхности энергии к другой. Другими словами, внешняя сила F

меняет не только квазиимпульс, но и энергию частицы. К вопросу

об изменении энергии можно подойти, рассматривая уравнение Шре-

дингера, что будет проведено ниже.

Вернемся к оператору ускорения. Для этого вычислим скобку

Пуассона, учитывая, что на кристалл наложено «внешнее» потен-

циальное поле V (г). Обозначим гамильтониан поля решетки Н

= —g-A + t/(r), (14.10)

для полного гамильтониана имеем выражение

H = -^A + U(r) + V(r) = U

+V(r). (14.11)

Так как оператор cKopocm-v коммутирует с Н

, то для опера-

тора ускорения получим

а = dw/dt = (1ЦК) {ν (Н

+ V) - (Но + V) v} = (vV - Vv).

(14.12)

Удобно выразить а в к-представлении. Учитывая, что

ν (к) = άΕ/Ηάκ, (14.13)

запишем

• aW^^^VM-Vwf-}; (14.14)

Чтобы вычислить из (14.14) а (к), надо задать потенциальную

энергию в к-представлении. Для этого в потенциальную энергию,

заданную в виде функции от координаты

—

V (г), необходимо подста-

вить г в к-представлении, т. е. вместо г надо подставить оператор

г (к) =

— /

In φκ). (14.15)

Рассмотрим наиболее важный практически случай однородного

силового поля

K(r) = -(F

r). (14.16)

В к-представлении оно будет иметь вид суммы оператора диффе-

ренцирования по к и оператора умножения:

V (к) = — I (F

) + i (F

In φ*). (14.17)

Пёк

Так как второй член в (14.17) коммутирует с-^-, то

ft (К) •=- W {ж (-

«) - Wa

VK)

= (l/й

) (F

VJE) = F

/m*.

(14.18 )

Величина

Λ = = ' (14.19)

ш* αΡ

v 7

может рассматриваться как обобщенный тензор обратной эффек-

тивной массы, который при квадратичной зависимости энергии от

квазиимпульса совпадает с введенным ранее тензором т*

-1

Учитывая (14.19), запишем

а (к) = F

/m* (к). (14.20).

Так как F

не зависит от к, то при не зависящей от к эффек-

тивной массе а будет иметь один и тот же вид в любом представ-

лении:

a = F

/m*; a = F

/m*, (14.21)

или

m*a = F

; m*a = F

. (14.22)

Уравнение (14.21) или (14.22) по форме совпадает с уравнением

движения Ньютона. Однако уравнение (14.21) или ,(14.22) имеет ряд

особенностей, на которые необходимо обратить внимание.

Во-первых, т* является в общем случае тензором второго ранга,

поэтому вектор ускорения не совпадает по направлению с вектором

силы. Уравнение (14.21) имеет вид, например, для а

Если m*"

имеет диагональный вид, то

= Fj/mj. (14.24)

Уравнение (14.24) показывает, что ускорение будет коллинеарно

силе только в том случае, когда сила направлена по одной из осей

эллипсоида энергии.

Во-вторых, ускорение сообщается электрону только внешней си-

лой F

, внутренние силы F/ никакого ускорения электрону не сообщают.

В-третьих, динамической характеристикой электрона, определяю-

щей его реакцию на действие внешних сил, является эффективная

масса т*, а не обычна.β масса. Это означает, что несмотря на то,

что поле решетки не ускоряет электрон, оно оказывает воздействие

на изменение его движения под действием внешних полей. Другими

словами, при действии внешних сил пом решетки проявляет себя

тем, что динамические свойства электрона определяются не обычной

его массой, а массой эффективной.

Для скалярной эффективной массы а и F

коллинеарны. Но отли-

чие электрона в решетке от свободной частицы заключается не толь-

ко в отличие величины эффективной массы от массы свободной час-

тицы. В том случае, когда частица находится в окрестности макси-

мума энергии, эффективная масса отрицательна, и ускорение а нап-

равлено против внешней силы F

а = F

/m* = — F

/j m* (14.25)

Рассмотрим силу, вызываемую однородным электрическим полем

F« = £,JE, (14.26)

где е

—

заряд электрона (е

<0). В этом случае

а = = Е = ^гЕ. (14.27)

т*

—\т* |

|m*|.

v 7

Ускорение, которое испытывает электрон в электрическом поле,

направлено по полю, т. е. так, как если бы электрон имел положи-

тельный заряд и положительную эффективную массу. Такой аномально

ускоряемый электрон будем называть квантовомеханической дыркой.

Если же электрон находится в окрестности минимума энергии,

то т* > 0, и ускорение направлено по силе, т. е. против поля Е,

как и для обычного электрона:— ? . '

Выражение (14.22) можно получить из (13.19). Действительно,

дифференцируя (13.19) по времени, получим

4V = = =

(14

28)

dt dt m* m* dt m*

a x

Выражение (14.28) совпадает по форме с (14.21), однако оно бо-

лее общее, чем (14.21), где ¥

предполагается независящей от коор-

динат, в то время как в (14.28) F

может быть функцией координат.

Но с другой стороны т*"

в (14.21) является обобщенным тензором

обратной эффективной массы, а в (14.28) т*-

не зависит от к. Дру-

гими словами, уравнение (13.19) и, следовательно, (14.28) справед-

ливо до тех пор, пока состояние Р —Р

находится в области квад-

ратичной зависимости энергии от квазиимпульса; если же состояние

перемещается в область, где энергия является более сложной функ-

цией квазиимпульса, то в (14.28) необходимо добавить производную

от т*

по времени.

В заключение этого параграфа запишем выражение для среднего

(в квантовомеханическом смысле) значения импульса в стационарном

состоянии , описываемого функцией Блоха ψ

(г):

(ρ) = $Ψ!(Γ)ΡΨΕ(Γ)Λ =

/Η

$ιΚ£*Μτ =

/η<ν>.

(14.29)

Но, согласно (13.16) и (13.19),

поэтому

или

(ρ)=^ (Ρ - Ро); Ρ -

Ρο

= ^ (ρ>, (14.31)

Pi-Pv^W. (14.32)

Таким образом, понимая под (ρ) «классический» импульс элек-

трона в решетке, можно выразить квазиимпульс через «классический»

импульс и эффективную массу.'

Сравним величину кинетической энергии свободной частицы,

имеющей импульс <р), с полной энергией электрона в решетке,,

имеющего тот же средний импульс, что и у свободной частицы:

Т-^-Т-Т^Г· .««Ί

Для скалярной эффективной массы

= m* и

' Т = ^[Я(Р)-£(Р

)]. (14.34)

Резюме § 12— 14

1. Важнейшим понятием, используемым для описания движения

электрона в твердом теле, является понятие эффективной массы т*.

Она определяется как тензор, обратный тензору обратной эффектив-

ной массы т*

-1

. Тензор обратной эффективной массы т*

есть ве-

личина, равная второй производной от энергий по квазиимпульсу:

* ι 1 (РЕ ' /чл ι \

= (

·!Ρ)

поэтому

m* = {cPE/dP

. (14.2р)

Если m*

имеет диагональный вид: {т*~

}ц = тг

, то т* также

диагонален, причем

ту = rriibij. (14.Зр)