Киреев П.С. Физика полупроводников

Подождите немного. Документ загружается.

В системе единиц СИ электропроводность измеряется в симен-

сах (Сим), а удельная электрическая проводимость

—

в Сим/м. Раз-

мерность подвижности в СИ можно найти из (1.8):

[μ] = (А-с

) кг-

Подвижность можно ' измерять также величиной скорости в еди-

ничном поле, т. е. величиной с наименованием м/с: В/м = м

/(В-с).

В лабораторной практике чаще используют внесистемные единицы

(см, 'В, с) и измеряют подвижность в см

/(В-с), а удельную элек-

трическую проводимость' в Ом"

см

-1

. Очевидно, что

1 м

/(В

с) = 10

см

/(В

с);

Сим/м = ΙΟ"

1/(Ом

см).

Резюме§1

1. Основные положения классической электронной теории про-

водимости- сводятся к следующему:

а) электроны образуют идеальный (электронный) газ, находя-

щийся в хаотическом тепловом движении, которое характеризуется

средней длиной свободного пробега I и средним временем свободного

пробега τ;

б) электроны обмениваются. энергией и импульсом с ионами-

решетки, благодаря чему электронный газ находится в термодина-

мическом равновесии с решеткой;

в) электрическое поле сообщает электронам направленное дви-

жение, тем самым вызывает электрический ток.

2. Плотность тока пропорциональна напряженности электри-

ческого поля:

j = σΕ. (1.1 ρ)

3. Удельная электрическая проводимость связана с концентра-

цией η и подвижностью μ электронов соотношением

σ = βημ. (1.2р)

4. Подвижность определяется характеристиками электрона и

хаотического движения (в ςлaбыx полях):

μ = ex/2 т = el/2mvr. (1 .Зр)

5. Подвижность численно равна скорости дрейфа в электрическом

поле единичной напряженности:

μ = ν

/Ε. (1.4р)

6. В сильных электрических полях закон Ома может нарушаться.

7. Время свободного пробега можно рассматривать как время

релаксации.

§ 2. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ ВРЕМЕН

И ДЛИН СВОБОДНОГО ПРОБЕГА

Выражения для подвижности и проводимости, полученные в пред-

положении одинаковости времени свободного пробега для всех электро-

нов, необходимо преобразовать, учитывая, что в действительности будут

наблюдаться самые различные времена свободного пробега, меняю-

щиеся от 0 до оо. Для этого, необходимо знать вероятности опреде-

ленных значений времен свободного пробега, которые рассматри-

ваются как случайные величины. Найдем функцию распределения

времен свободного пробега.

Для этого предположим, что:

1) .

вероятность испытать столкновение {рассеяние) в течение

интервала времени dt для электрона пропорциональна величине интер-

вала dt;

2) вероятность столкновения в единицу времени

—

постоянная во

времени величина.

Этих двух предположений достаточно для получения функции

распределения времен свободного пробега. Обозначим вероятность

того, что частица двигалась без столкновения в течение вре-

мени t, t + dt, через

dw = dw (dt). (2.1)

Величина w(t) есть вероятность свободного движения в интер-

вале времени (t

t-\- 1), a w(t-\- dt) есть вероятность свободного дви-

жения в интервале t + dt, t-\-dt-\-1. Но величину w(t-1- dt) можно

выразить двояко. С одной стороны,

w(t + dt) = w(t) + ^-dt. (2.2)

С другой стороны, факт свободного движения в течение времени

t + dt

—

событие С —можно рассматривать как произведение двух

событий: Л —свободного движения в течение времени t и В— сво-

бодного движения в течение времени dt; так что

С = АВ. (2.3)

Вероятность произведения двух событий есть произведение веро-

ятности одного на условную вероятность другого:

w(C) = w (A) w (В/A) = w(B)w (А/В). (2.4)

Но так как событие А не зависит от события В, то

(А/В) =

= w(A). Вместе с тем событие В оказывается не зависящим от Л*,

поэтому

w(t + dt) = w (t). dw (dt). (2.5)

* Утверждение о независимости события В от события А (в нашем случае),

как правило, вызывает у изучающих резкое возражение, в то время независи-

мость события А от В принимается как очевидный факт. Основным аргументом

обычно выдвигается утверждение, что если частицы рассеиваются за время, мень-

Вероятность свободного движения за

время dt можно выразить

через вероятность рассеяния за то же время. Обозначим вероят-

ность рассеяния (соударения) за единицу времени через а, тогда

вероятность рассеяния за время dt будет равна adt, а вероятность

свободного движения будет равна

1 — adt>

т. е.

dw{dt)=l-ctdt. ' (2.6)

Учитывая выражения (2.2), (2:5) и (2.6),' можно записать

w(t + dt) = w(t) + ^dt==w(t)[l-~ adt] = (t) - w (t) adt, (2.7)

что приводит к дифференциальному уравнению для функции w(t)

dw/dt = — wa. (2.8)

Решая уравнение (2.8), получим

w (t) = ct~

. (2.9)

Константа интегрирования с определяется из условия нормировки

оо оо

[w(t)dt=l=c^ e~

dt = (2.10)

о о

откуда

с = а. (2.11)

Таким образом, нормированная функция распределения времен сво-

бодного пробега имеет вид

w (t) = ae~

. (2.12)

Найдем среднее время свободного пробега (/): ,

00 00

<0 = J tw (t) dt= J tae-

dt = ±. (2.13)

0 0 . ' ·

Если обозначить среднее время свободного пробега через τ: (t) = τ,

т о согласно (2.13) вероятность столкновения за единицу времени

равна обратному среднему времени свободного пробега: /

•

= | = (2.14)

Нормированная к единице функция распределения может быть

записана в виде

w(t) = ±e - (2.15)

шее t, то ни о каком движении за время dt после t говорить нельзя. Но в этом

случае нет не только события В, но и С и даже Л, в то время как теорема

формулируется для события ЛВ = С, а произведение двух событий есть осу-

ществление обоих событий — сомножителей.

Аналогичным образом можно йаити функции) распределения длин

свободного пробега χ:

где I —средняя длина свободного пробега.

Полученные функции распределения справедливы для самых

общих случаев. Применим их для случая движения электронов

в электрическом поле. Нас будет интересовать при этом только

направленное движение электронов против поля. Пусть ось χ сов-

падает по направлению с полем. Электрон, двигаясь в поле, за время

свободного движения t приобретает скорость

v(t)= —Ε

' т

и проходит путь длиной х:

]L /2. ν

—

№

~2т

' 2т *

Средняя скорость дрейфового движения

ОО СО 2

ν, = ^ ν (0 ю (0 dt=

| \ te~% % =Ε, (2Л9)

О о

а среднее перемещение против поля

СО СО f

1= $

•И»

(0 л =

Τ ='Έ

•• $

О О

Мы видим, что скорость дрейфа равна

где

(2.22)

есть подвижность.

Выражение (2.22) для подвижности отличается от ранее наиде*

кого значения (1.8) множителем 2, обусловленного тем, что в (2.2'

учтен больший вклад движении с большими временами свободнс

пробега. Это особенно отчетливо видно из выражения для среди·

смещения:

так как всегда

в данном случае

В заключение этого параграфа необходимо сделать одно простое,

о очень существенное замечание: τ есть среднее время свободного

пробега, т. е. время между двумя соударениями. Оно определяется

длиной свободного пробега и полной скоростью частицы, но не ско-

ростью дрейфового движения. Полная скорость зависит от энергии

частицы. Тем самым время свободного пробега является функцией

энергии частицы. Эта зависимость усложняется в том случае, когда

длина свободного пробега также зависит от энергии. Поэтому для

нахождения дрейфовой скорости, как и целого;ряда других харак-

теристик вещества, необходимо усреднять времена свободного про-

бега и другие величины с учетом функции распределения электро-

нов по энергии, что будет проделано в IV главе.

Резюме § 2

1. Для получения функции w(t) достаточно предположить, что:

а) вероятность рассеяния в течение времени dt пропорциональна dt\

б) существует независящая от времени вероятность рассеяния в еди-

ницу времени, равная а.

2. Времена свободного пробега вследствие случайного характера

столкновения могут принимать различные значения. Вероятность

того, что время свободного пробега лежит в пределах t,t-\-1, равна

= (2Лр)

3. Среднее время свободного пробега τ и вероятность соударе-

ния за единицу времени а связаны между собой соотношением

ατ= 1. (2.2р)

4. Вероятность того, что длина свободного пробега лежит в пре-

делах χ, x+\

равна *

(

)

-T. (2.3р)

5. Средняя длина свободного пробега I связана с вероятностью

рассеяния на единице длины Ь соотношением

М= 1.

6. Если учесть статистический разброс времен свободного пробега

и учесть, что большие времена свободного пробега в силу квадра-

тичной зависимости пути от времени дают больший вклад в прово-

димость, то для подвижности получим выражение

μ = ет/т.

(2.4р)

§ 3. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ ЭЛЕКТРОНОВ ПО СОСТОЯНИЯМ.

СРЕДНИЕ ЗНАЧЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН

Пространство координат х, у, ζ и импульсов р

Х1

, р

называют

фазовым пространством. Рассмотрим в фазовом пространстве элемент

объема

dT = dx dy dz dp

= dx

, (3.1)

построенного вокруг точки с координатами (л:, у, z\ р

> р

уу

ЧИСЛО электронов* dN, находящихся в этом элементе объема, должно

быть пропорционально величине объема dT, если dT достаточно

мало. Кроме того, это число должно зависеть от точки (г, р) фазо-

вого пространства, оно определяется некоторой функцией F (г, р, t),

так что

dN = F(r,p

t)dT. . (3.2)

Интегрируя по всему фазовому пространству, получим полное

число электронов N:

N = \ F(r,p,i)dT. (3.3)

(

τ)

Функция F(г, р, t) определяет число электронов в единице объема

фазового пространства. Вместо нее можно ввести функцию

(г, р, t)

в N раз меньшую:

/(Г. P. f) = jfF(r, ρ, 0. (3.4)

Функция f(г, ρ, определяет вероятность нахождения одного

электрона в единичном объеме фазового пространства, а равенство

(г, р, 0 ^Г =

- (3.5)

(

τ)

называют условием нормировки.

Интегрирование проводится по объему кристалла V и по всем

возможным значениям импульса. Условие нормировки не зависит

от времени, функция же распределения в общем случае зависит

от времени. С помощью функции распределения можно вычислять

средние значения произвольной физической величины, зависящей

от координат и импульса. Напомним, как производится это вычис-

ление. Пусть а —некоторая величина, которая может зависеть

от состояния движения электрона: a = a(r, р, t). Возьмем элемент

фазового объема В нем находится

dN = Nf (г, ρ, t) dT (3.6)

электронов, каждый из которых обладает величиной α (г, р, /).

Суммарное значение физической величины для dN электронов

равно

сс

dN. (3.7)

Если проинтегрировать (3.7) по всему фазовому пространству,

то получим суммарное для всех электронов значение величины а;

разделив эту величину на Ν, получим среднее значение (а):

<а>

= 1 J α dN = J «(г, р, 0 / (г, р, t) dT. (3.8)

(ν

) (ν

)

Если величину (3.7) проинтегрировать только по импульсу и

разделить на Ndx

, то получим среднее значение величины а(г)

которую имеют электроны в окрестности точки г.·

Отметим один практически важный частный случай. Пусть функ-

ция распределения не зависит от координат. В этом случае интегри-

рование по координатам соотношения (3.5) дает объем тела V, вслед-

ствие чего интегрирование по импульсу функции распределения

дает обратный объем. Если и α не зависит от координат г, то усред-

нение только по импульсу дает величину а? = где V

—

объем тела.

Плотность тока можно выразить через функцию распределения

следующим образом:

j = еп (ν) = enV \ vf (г, ρ, t) dx

= env

. (3.9)

Λ — oo

^^ Если /(r, p, t)=f(r, —p, t)

что означает равновероятность

гч. движений со скоростями ν и —ν, то средняя скорость (ν) в силу

jsj^нечетности функции г, р, t) при интегрировании в симметрич-

г^чных пределах равна нулю.

) Для металла, находящегося в состоянии термодинамического рав-

новесия, движение электронов описывается четной (симметричной)

функцией распределения. Отсюда следует хорошо известный факт,

что тепловое движение не приводит к возникновению тока. Для его'

появления необходимо создать условия, при которых нарушается

симметрия функции распределения, благодаря чему одни направле-

ния скоростей становятся более вероятными, чем другие. Это приво-

дит к тому, что вся совокупность электронов должна перемещаться

в пространстве; на хаотическое движение должно быть наложено

направленное движение электронов, которое

может быть

вызвано

различными причинами: электрическим полем, градиентом темпера-

туры, неоднородным освещением и т. п.

Функция распределения электронов по состояниям в общем слу-

чае должна быть найдена из "кинетического уравнения Больцмана,

о котором будем говорить при описании кинетических явлений

в полупроводниках.

Для равновесного состояния системы квантовая статистика при-

водит к следующему выражению (f = f

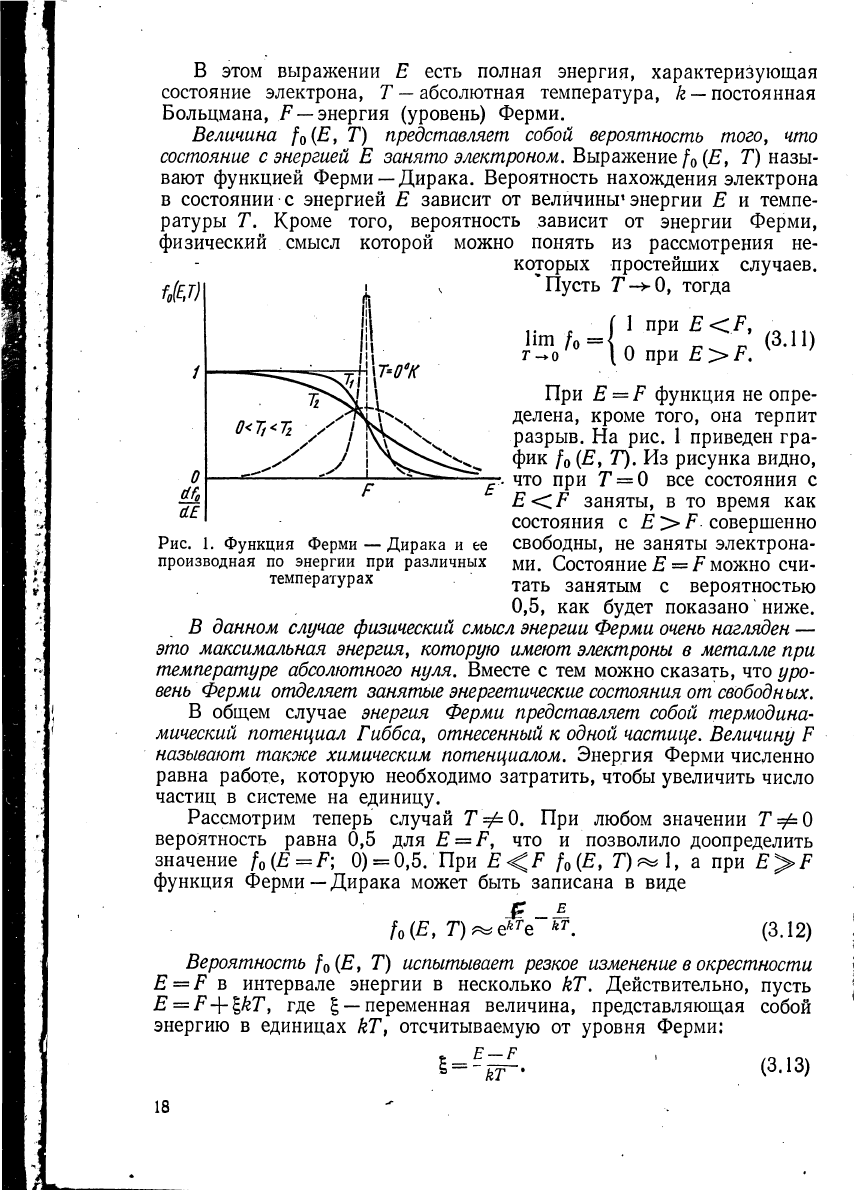
В этом выражении Ε есть полная энергия, характеризующая

состояние электрона, Г —абсолютная температура, k

—

постоянная

Больцмана, /'

—

энергия (уровень) Ферми.

Величина f

(E, Τ) представляет собой вероятность того, что

состояние с энергией Ε занято электроном. Выражение /

(Е, Т) назы-

вают функцией Ферми —Дирака. Вероятность нахождения электрона

в состоянии с энергией Ε зависит от величины

энергии Ε и темпе-

ратуры Т. Кроме того, вероятность зависит от энергии Ферми,

физический смысл которой можно понять из рассмотрения не-

которых простейших случаев.

Ф)

I 1

\ T=0°K

0<Т,<Т

У у

\ T=0°K

F E'

Пусть Т~*0у тогда

lim

при Ε <F,

при E>F.

(3.11)

dfo

Рис. 1. Функция Ферми — Дирака и ее

производная по энергии при различных

температурах

При Ε = F функция не опре-

делена, кроме того, она терпит

разрыв. На рис. 1 приведен гра-

фик

/о

(Е> Т). Из рисунка видно,

- что при Т

—

0 все состояния с

E<CF заняты, в то время как

состояния с E>F совершенно

свободны, не заняты электрона-

ми. Состояние £== F можно счи-

тать занятым с вероятностью

0,5, как будет показано

ниже.

В данном случае физический смысл энергии Ферми очень нагляден —

это максимальная энергия, которую имеют электроны в металле при

температуре абсолютного нуля. Вместе с тем можно сказать, что уро-

вень Ферми отделяет занятые энергетические состояния от свободных.

В общем случае энергия Ферми представляет собой термодина-

мический потенциал Гиббса, отнесенный к одной частице. Величину F

называют также химическим потенциалом. Энергия Ферми численно

равна работе, которую необходимо затратить, чтобы увеличить число

частиц в системе на единицу.

Рассмотрим теперь случай Τ Φ 0. При любом значении Τ Φ 0

вероятность равна 0,5 для E = F, что и позволило доопределить

значение f

(E=F\ 0) = 0,5. При f

(E, Т)ъ*1

а при £>/?

функция Ферми—Дирака может быть записана в виде

fo(E, Τ) ,

;e*

(3.12)

Вероятность f

(E, Τ) испытывает резкое изменение в окрестности

E = F в интервале энергии в несколько kT. Действительно, пусть

Ε = F + lkT

где ξ —переменная величина, представляющая собой

энергию в единицах kT, отсчитываемую от уровня Ферми:

Ε — F

(3.13)

В таком случае

(3.14)

В табл» 1 приведена величина /

(Ю Для нескольких значений ξ.

Таблица!

-5

—4 —3

—2 —1

/о

0,994

0,980 0,954

0,882

0,730

0,600

0,270 0,118

.0,048

0,018

0,007

На рис. 2 приведен график /

(£),-из которого видно, что функ-

ция Ферми —Дирака испытывает сильное изменение: от 0,88 до 0,12 —

при изменении ξ в интервале от —2 до 2. Другими словами, сущест-

венное изменение функция распределения f

(E, Τ) испытывает при

изменении энергии отF

—

2kT до F + 2kT, и при ξ<—2,

а при ξ> 2 она ведет себя подобно

экспоненте.

Интервал энергии, определяющий

резкое изменение f

(E, Τ), зависит

от температуры: при Т-^0 он стре-

мится к нулю. Для характеристики

изменения функции распределения

удобно использовать ее производную

по энергии

f ^ _ 1 1

-dE~dl \дЕ~~ 2kT *

+ ch ξ'

(3.15)

где ch£

е^ +

е-^

-6-5-Ϊ-3-2-1 0 1 2 3 ϊ 5 НТ

Рис . 2. Функция Ферми — Дирака.

Энергия выражена в kT и от-

считывается от уровня Ферми

При Τ

-»•

0 всюду, кроме Ε =

= F (ξ = 0), chg->oo и поэтому при

Τ Φ 0 /о£ будет отлична от нуля только в малой окрестности точки

ξ = 6. В пределе 0 эта окрестность стягивается в-одну точку

1 = 0, так что

а/

(£, 0) „(

со при E = F,

0 при

при этом

-< J Κε(Ε,0)άΕ = \..

(3.16)

(3.17)

Выражение (3.17) справедливо при любой температуре Т^О.

Мы видим, что —Гое{Е, 0) представляет собой δ-функцию Дирака.

При Г>0 функция КяФ, Τ) будет тем ближе к δ-функции, чем

меньше температура. На рис. 1 (пунктирная линия) дан график

Гое(Е, Т) при разных температурах.

Квантовые системы, описываемые функцией Ферми—Дирака, назы-

вают вырожденными.

Рассматривая большие значения ξ, видим, что /

может быть

представлена экспоненциальной функцией

(3.18)

(3.19)

Функцию

/о

(Ε, Т) = e

-e

называют классической функцией

распределения, или функцией Больцмана. Системы, описываемые

функцией Больцмана, т. е. подчиняющиеся классической статистике,

называют невырожденными. Отличие классической функции распреде-

ления от квантовой состоит не только в различии функционального

выражения, но имеет более глубокий смысл, связанный, в частности,

с возможностью в классической физике раздельного определения

кинетической и потенциальной энергии, что невозможно в кванто-

вой физике, в которой измеряется лишь полная энергия.

Для вычисления средних значений физических величин с исполь-

зованием функций распределения [

(Е, Т) необходимо знать связь

между энергией и скоростью (или импульсом р) частиц. Предполо-

жим, что для свободного электронного газа

= s(3-20)

Так как энергия не зависит от направления импульса, то эле-

мент объема в пространстве импульсов dx

= dp

удобнее

выразить в сферической системе координат:

= p

dpdQ = p*dpsinQdBdy. (3.21)

Интегрирование по углам θ, φ дает множитель 4π.

Рассмотрим случай статистики Больцмана и вычислим среднее,

значение энергии электрона:

tovJgLrs&Vrfp

<£> = — · (3.22)

4nV ^ е

2mkT

ρ- dp

foil)··

или

ΜΕ, Τ) e