Киреев П.С. Физика полупроводников

Подождите немного. Документ загружается.

т е

. полосы энергии Е~ и Е

перекрываются. Но это означает, что

спектр энергии в этом случае непрерывен.

Для того чтобы возник интервал запрещенных значений в спектре

энергии, необходимо, чтобы перекрытия полос не происходило. Эта

возможность становится очевидной, если учесть существование дру-

гих граничных поверхностей.

Рассмотрим качественно особенность характера энергетического

спектра в окрестности одной из вершин зоны Бриллюэна. Пусть

границы зон заданы тремя уравнениями:

(gi,

Koi

+ ttgxHO,

Ko2

+ rcg

) = 0,

Коз

+ л£

) = 0,

(17.50)

где gi, g2

—

некоторые векторы обратной решетки; κ

χ, к

, κ

οθ

—

текущие радиус-векторы соответствующих граничных плоскостей.

Так как для состояний на граничных плоскостях скорости лежат

в самих плоскостях, то для состояний, определяемых линией пере-

сечения двух плоскостей, скорость может- быть направлена только

по этой линии. Если же рассмотрим состояние, соответствующее

точке κδ пересечения трех плоскостей, то. скорость ν(κβ) может быть

равна только нулю, т. е. в вершине зоны Бриллюэна должен быть

экстремум энергии, так как в ней

-Si г

(,7

Мы видим, что разложение в ряд Тейлора для экстремумов,

лежащих в вершинах зон, не будет содержать линейных членов.

Считая векторы g

и g

взаимно ортогональными, можем найти

приближенное выражение для энергии в окрестности точки κδ.

Одновременно должны быть справедливы три уравнения:

1 П* / jt

g?· \

(к) = (Κδ) + — — zb^IT^J-) <

δ)

0=1.

> 3)· (

·52)

Для того чтобы они удовлетворялись одновременно, необходимо,

чтобы каждое из них было справедливо, для проекций (к

—

к§)

на соответствующие векторы g

так что

Е± (к) =£± (κδ) ± 2 ЙГ (

^ m^j) <*"*Ь>

= Е

(ко) ± 2 (17.53)

Ни

этом ПЛЮС И МИН

УС должны относиться к состояниям внеш-

и внутренним для каждой поверхности. Величина разрыва

будет разной для различных направлений. Термической шириной

запрещенной зоны будет минимальная величина из трех (2

U|)

поскольку она определяется минимальным энергетическим зазором*

существенным для явлений электропроводности. Для явлений, в кото-

рых существен закон сохранения квазиимпульса, ширина запрещен-

ной зоны должна изменяться от минимальной до максимальной

величины из (2|[/

, |).

Наличие разрыва в спектре энергии становится очевидным

из самого выражения для энергии —при смещении от точки лсо энер-

гия или возрастает по сравнению с £

(ко), или уменьшается по срав-

нению с £-(ко), а Ε (ко) в данном случае не может изменяться, в то

время как при разрыве энергии в точках граничной плоскости изме-

нение энергии достигается за счет изменения Ε (к

) и линейного члена.

Для получения более точного выраже-

ния для энергии в окрестности вершин

зон Бриллюэна'необходимо учесть четы-

рехкратное вырождение энергии, в силу

чего волновую функцию нулевого прибли-

жения надо брать в виде.

f>(r (17.54)

где

^ (г) = ^ е<

(кг)

; (г) = -±= е*"+'

(/=1,2,3). (17.55)

Для определения Ε (к) получим уравнение четвертого порядка.

В заключение рассмотрим форму изоэнергетических поверхностей

в зонах Бриллюэна и зависимость энергии от к вдоль некоторых

направлений.

Вблизи центра первой зоны Бриллюэн.а при к = 0 поверхности

энергии являются сферами (на рис. 17 приведены поверхности энер-

гии, т. е. изоэнергетические линии, для плоской решетки). По мере

удаления от центра сферы начинают деформироваться. Характер

деформации можно понять, если рассмотреть поверхности энергий

в углах зон, где они должны быть частью поверхности эллип-

соида.

Рассмотрим теперь зависимость энергии от

для некоторого

направления. Поскольку изоэнергетические поверхности имеют слож-

ную форму, графики, выражающие зависимость энергии от

лЯ

разных направлений, будут разными. На рис. 18 представлена

зависимость Ε (к) для одного из осевых направлений, перпендику*

лярных границам зон Бриллюэна. Пунктиром обозначена зависи-

мость Е° (к) для свободного электрона. Расстояние до границы Д

лЯ

различных направлений различно, поэтому положение точки, гД

Рис. 17. Изоэнергетические

линии для квадратной пло-

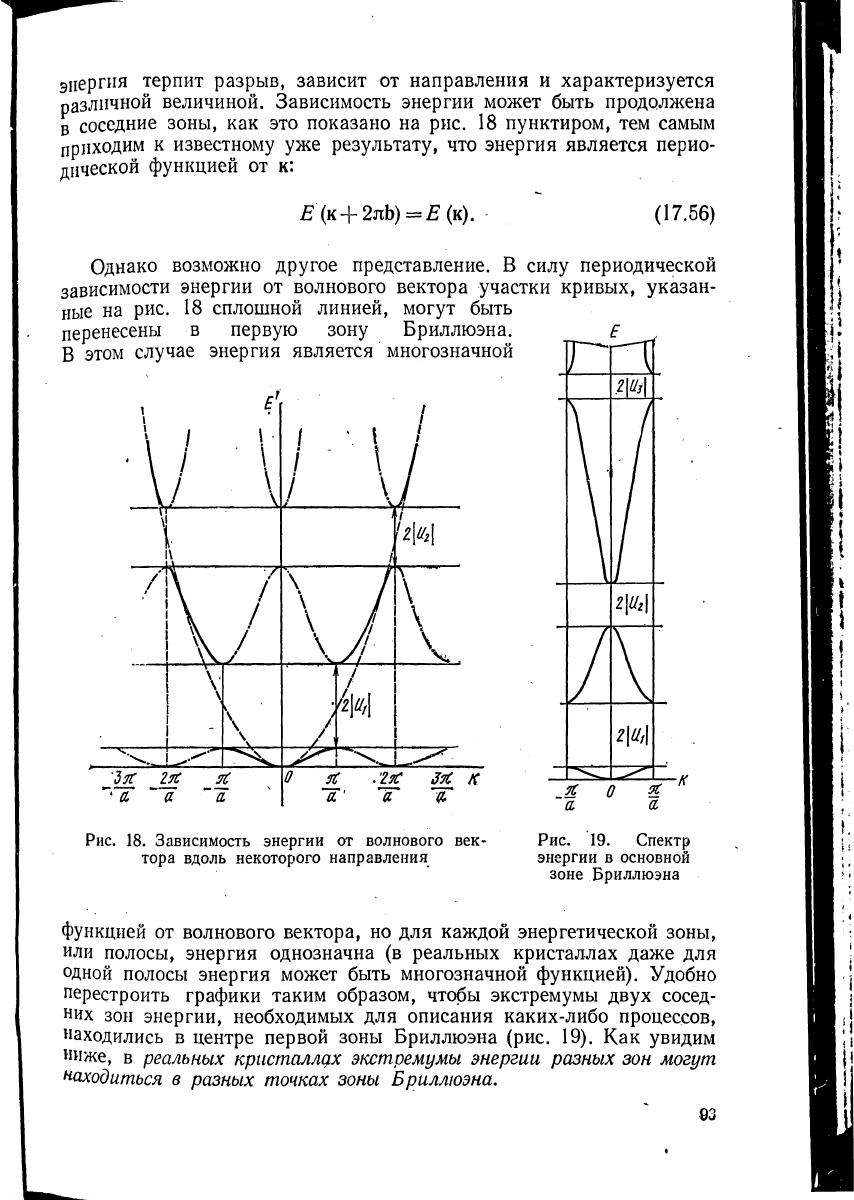
энергия терпит разрыв, зависит от направления и характеризуется

различной величиной. Зависимость энергии может быть продолжена

в соседние зоны, как это показано на рис. 18 пунктиром, тем самым

приходим к известному уже результату, что энергия является перио-

дической функцией от к:

£'(к + 2лЬ) = £(к). - (17.56)

Однако возможно другое представление. В силу периодической

зависимости энергии от волнового вектора участки кривых, указан-

ные на рис. 18 сплошной линией, могут быть

тора вдоль некоторого направления энергии в основной

зоне Бриллюэна

функцией от волнового вектора, но для каждой энергетической зоны,

или полосы, энергия однозначна (в реальных кристаллах даже для

одной полосы энергия может быть многозначной функцией). Удобно

перестроить графики таким образом, чтобы экстремумы двух сосед-

них зон энергии, необходимых для описания каких-либо процессов,

находились в центре первой зоны Бриллюэна (рис. 19). Как увидим

ниже, в реальных кристаллах экстремумы энергии разных зон могут

находиться в разных точках зоны Бриллюэна.

Резюме § 17

1. В теории квазисвободного электрона в качестве нулевого

приближения для электрона в периодическом поле принимается

решение уравнения Шредингера для свободного электрона:

, ' <

·ΐρ>

Шг)=у=е<<->. (17.2ρ)

2. Потенциальная энергия поля решетки рассматривается в каче-

стве возмущения

W (г) = U (г). " (17.3р)

Матричные элементы оператора W, вычисленные с помощью волно-

вых функций Ψ£(γ), отличны от нуля, если к' = к + 2лЬ; они равны

при этом коэффициентам разложения U (г) в ряд Фурье:

= U

= c

; b-^i. (17.4р)

Для малых значений

величинна Uъ будет больше, чем для

больших |Ь|, посксэльку большие значения |Ь| соответствуют «гармо-

никам» поля U (г) более высокого порядка.

3. В первом приближении теории возмущения спектр энергии

смещается вниз на величину (U>. Во втором приближении для боль-

шинства состояний поправка к энергии практически равна нулю.

Но существуют состояния, для которых поправки к энергии и вол-

новой функции обращаются в бесконечность. Физически это озна-

чает, что такие состояния вырождены.

4. Вырожденные состояния к лежат в плоскостях, которые удов-

летворяют уравнению

(Ь, к + яЬ) = 0, (17.5р)

представляющему собой уравнение Вульф —Брэгга. Эти плоскости

удобно выбрать в качестве границ зон Бриллюэна. Решение задачи

методами теории возмущений для вырожденных состояний показы-

вает, что энергия терпит разрыв величиной 2

в точках вырож-

дения, т. е. на границах зон Бриллюэна.

5. Разрыв в энергии приводит к разрыву в спектре энергии,

возникают запрещенные значения энергии, которые называются

запрещенными зонами.

Ширина запрещенной зоны равна 2|1/ь|> поэтому она растет

с ростом потенциального поля U (г). С ростом энергии Ε ширина

запрещенных зон уменьшается, а ширина зон энергии увеличива-

ется (см. рис. 19).

6. Физической причиной образования зонной структуры спектра

является вульф.-брэггова интерференция электронных волн.

7. Эффективная масса имеет различный знак в максимуме

и минимуме энергии^Пренебрегая единицей по сравнению с другим

членом в знаменателе выражения (17. 45), получим

пг

/** g2

(17.6р)

Из (17.бр) следует, что: а) \т*\ пропорциональна ширине запре-

щенной зоны; б) с ростом энергии

уменьшается, т. е. в более

высоких зонах энергии

меньше, чем в более низких.

8. Энергия является квадратичной функцией волнового вектора

в окрестности экстремумов. Поверхности энергии ортогональны гра-

ницам зон Бриллюэна.

§ 18. ТЕОРИЯ КВАЗИСВЯЗАННОГО ЭЛЕКТРОНА

В теории квазисвязанного электрона при решении уравнения

Шредингера для электрона в периодическом поле

Ηψ(Γ)«£ψ(Γ),

Η*

Η = + U (г) = U (г + п)

(18.1)

за нулевое приближение принимается состояние электрона в изо-

лированном атоме. Обозначим га-

мильтониан изолированного атома

через Н

№

2т

Δ + УЛг) (18.2)

и запишем уравнение Шредингера

для атома

HA(r) = tt(r), (18.3)

где V

(г) — потенциальная энергия

электрона в изолированном атоме;

?о

—

энергия некоторого уровня,

Рис. 20. Потенциальная энергия и

уровни изолированного атома

Ψα

(г) — соответствующая уровню Ε а

волновая функция. На рис. 20 по-

казана схема уровней энергии изо-

лированного атома. Отличительной особенностью атомной волновой

Функции является ее резкая зависимость от расстояния: начиная

с некоторых значений г, волновая функция уменьшается по экспо-

ненте. Решение уравнения для атома считается известным. Для

нахождения энергии электрона в кристалле в первом приближении

необходимо подобрать волновую функцию в нулевом приближении.

^ этой целью предположим вначале, что атомы кристалла не взаимо-

действуют друг с другом. Совместим начало координат с каким-либо

ядром, тогда координаты остальных ядер можно представить в виде

вектора трансляции:

η =

η,χ&χ

+ «2

2 + Яз

з·

Если обозначить текущий радиус-вектор через г, то расстояние

между данной точкой г и ядром η равно

—

η волновая функция

электрона в,п-ом атоме запишется в виде ψ

(Γ —п).

Волновая функция электрона в кристалле (г) должна быть

образована из атомных волновых функций ψ

(Γ—п):

(Γ) = 2^ψα(Γ-Πΐ). (18.4)

Коэффициенты с

выбираются таким образом, чтобы (г) удовлет-

воряла трансляционному условию

(г + п) = е'

(κη)

(г), (18.5)

где п—-вектор трансляции и к —волновой вектор. Для того чтобы

трансляционное условие выполнялось, с

можно выбрать в виде

Ст==е

Ккт)

, (18,6)

или

\])0(

)

Km)

ij>

(r-m). (18.7)

Проверим, выполняется- ли условие (18.5) для функции.(18.7):

ψο

(r-f

п)

= 2

(г -

+ η) =

πι

кп

>]£е

{(к

п)

ψα

[г

—

η)] =

е* <

κη

(ж1>

(

— 0

(

)

Очевидно, что

= ш —η пробегает те же значения, что и т,

только в другой последовательности, поэтому

2>'

(κ1)

ψα( г —1)=ψ°(Γ), ν (18.9)

и, следовательно, трансляционное условие выполнено.

Так как if>

(r —1) нормированы к единице, то -ψ

(г) не нормиро-

вана. Найдем ее нормировочный множитель:

(Г)Я|?°

(Г)dx =

р е-'

кт

ψ* (г - m) J p

e< <»>

(r -

n)~|

dx =

S Ψβ

(r - m)

Ψα

(г -

П)

dx. (18.1

m η

Двойная сумма легко сводится к одинарной сумме. Для этого

положим

—

m = r

; r = r' + m; dx = dx\ (18Л1)

тогда

$ψ2 (r-m) % (г η) dx =

= J ψα(Γ') [г' - (η - m)j dx'. - (18.12)

Интеграл от произведения волновых функций ^(г') и [г' — .

— (п

—

ш)] зависит не от положения ядер пит, а

только от рас- -

стояния t

—

m между

ними. Обозначим U(r)

(18.13)

При t = 0 S

= 1. Если

расстояние между ядрами

велико, то волновые функ-

ции не перекрываются и St

практически равны нулю.

Величины St будут отличны от нуля лишь для малых значений t.

Поскольку п

—

m и t пробегают одни и те же значения при фикси-

рованном т, то сумма- по η будет равна сумме по t:

е* <

(г - ш) % (г - п) dx = 2 е

. (18.14)

η t

Под знаком второй суммы стоят одинаковые члены вида

|^e

i(Kt)

StJ, их число равно Ν

—

числу атомов в кристалле. Следо-

вательно,

ψ*° (г) (г) dx = Ν Σ e

f(Kt)

St." (18.15)

Рис. 21. Поле решетки «растянутого» кристалла

Перейдем к нахождению вида оператора возмущения.

Предположим, что кристалл «растянут» столь сильно, что взаимо-

действие между атомами отсутствует. В этом случае периодическое

потенциальное поле кристалла есть периодически повторяющееся

потенциальное поле изолированного атома (рис". 21), поэтому

(18.16)

Отличительной особенностью этой суммы является то, что в каж-

дой точке г функция U (г) определяется только потенциальной кри-

вой ближайшего атома. При сближении атомов кристалла в каждой

точке г сумма потенциальных кривых изолированных атомов будет

по-прежнему давать потенциальную энергию электрона в поле всех

4 Киреев

ядер (рис. 22), но при этом не учитывается взаимодействие атомов

другими словами, сумма не является самосогласованной. Пуст^

самосогласование потенциальной энергии поля решетки достигается

посредством добавления некоторой энергии W (г) таким образом, ч

То

U(r)=%V

(r-n) + W(r). (18.7)

Функция W (г) является периодической, так как U (г)

—

n) —функции периодические; W(г) не имеет особых точек·

особые точки U (г) передаются атомными потенциальными кривы®

(г

—

п). Другими словами, W (п) близка к нулю, IF (г) всюду

ограничена. Аналитическое выраже-

ние для W (г) находится элементарно:

(г) = ί/ (г) _ Va(r-п) (18.18)

по «известным» U (г) и V

(r — η).

Величина W (г) будет меньше

нуля, пока атомы притягиваются,

и станет больше нуля, когда атомы

Рис. 22. Поле решетки кристалла начнут отталкиваться При очень

без учета взаимодействия электрон- сильном сжатии кристалла.

ных оболочек Перейдем к нахождению энер-

гии. Как известно, волновая функ-

ция в нулевом, приближении позволяет получить значение энер-

гии в первом приближении Е

{1)

U(r)

ihf

ауГ

Δ + 2 У а

(Г •-

п) + W (г) j (г) = £uy (г). (18.

19)

Умножая уравнение (18.19) на (г) и интегрируя его по объему

кристалла, получим

ψο

(г)

•£• •

Va(v

•+

w (г)

t° (г) dx

EW = —ι J

(18.20)

(Γ)ψ°(Γ)ί/τ . V

Знаменатель выражения (18.20) был ранее найден (см. 18.15).

Вычислим числитель, который обозначим через I:

ψο*

(г)

Г д

(г _ П) +

(Γ)1ψ° (г)

L η

= S {[Σ

(Kl>

^ (г -1) J ^ Δ + 2 У

(г -

П)

+ Г (гЛ X

χ ^ е'<*>% (г -1)| dx = ё<"· *

ψ* (г -1) χ

[- ш

•+

« ϊ-

У+

wj^»

(

}

άτ

· ^

21)

Положим

—

t = ρ; r = r+1; г

— 1

= r

; dx =

dx'\

= n-l; W(r) = W(r').

(

}

В таком случае интеграл I можно записать в виде одинарных

сумм:

! = N

»> Ψ* (г') £ Δ' + J

-Ю+'W (r')j Χ

(18.23)

подобно тому, как это было сделано при вычислений нормировоч-

ного члена для ψ°(ι*).

Учитывая, что

"-^-Δ'+1/

(γ'-Ρ) +

2 V

(r'-n') + W(r')jjt|;

(r'-p) =

= ^Ж(г'-р) + |2 У a(г'-гО + Г (r')j^(r'-p), (18.24)

можем записать

ι=л £ tf

(«ρ) ^

ψ* («ο +1 Σ

- ν -

')+Ψ ν - Ρ)}]

χψ

(г'-

ρ)

dY = ΝΕ

2 ёCP) 5ρ +

+ М^

1{кр)

\Га (Ο[Σ ν

(ϊ-η) + Ψ(Γ')\%(Γ'-ρ)άτ?. (18.25)

' Ρ [χι'φρ )

Выделим во втором слагаемом член с р = 0 и обозначим его

через С:

С =

Га (О { Σ

(Г

П')

(Г) j

(Г') d%\

(18.26)

Величина С представляет собой усредненную для некоторого

атома потенциальную энергию электрона в поле всех остальных ядер

с учетом самосогласованного характера поля. Теперь выражение для I

можно представить в следующей форме:

I = NE

J] е'

(кр)

+ NC + N Σ

е* <-*> \

(О X

Р Р

х\ Σ V

(f-TO + W(f)\y

(f--p)d*. (18.27)

Ln'^p J

Обозначим через A (ρ) интеграл в (18.27):

S ψα

(Ο Γ Σ У α (Γ' - η') + W (Ο ]ψα - ρ) Μ = Α (ρ). (18.28)

Ь'^р J

4* 99

А (ρ) есть обменная энергия, обусловленная тем, что каждый

электрон может быть найден с некоторой вероятностью у любого

ядра. Это проявляется в том, что в образовании А (р) участвуют

волновые функции двух атомов, отстоящих на расстоянии |р|. Дру

гими словами, два ядра, отстоящие друг от друга на расстоянии

могут обмениваться электронами.' Обмен происходит посредством

поля всех ядер, кроме двух данных ядер, и посредством периоди-

ческой самосогласующей части поля решетки W (г). Очевидно, что

А (р) существенно только при малых расстояниях |р|, так ^ак

в силу экспоненциального характера волновых функций А (р) о

при больших р. Физически это означает, что обмен в основном про-

исходит только между ближайшими атомами. Два любых атома

обмениваются электронами посредством последовательных обменов

соседних атомов. Другими словами, электроны не локализуются

у отдельных ядер, а «.свободно» перемещаются по кристаллу, пере-

ходя от атома к атому благодаря обменному эффекту. Кроме того,

следует заметить, что в образовании А (р) основную роль должно

играть периодическое поле W (г), достигающее заметной величины

в окрестности любого ядра, в то время как ^(г^ —п') при п'^0

и ri Φ ρ

—

величина малая в окрестности «обменивающихся» ядер.

Учитывая выражение для I можем записать выражение для энер-

гии ЕМ:

и \Е

2 +

е'

<-">

А (р)1

£(1) ^ L Ρ Ρ -I _

2><<

кр)

Л (ρ)

= Еа+Се'<«•>S

y +

(Kp)Sp

. (18.29)

ρ "

Мы видим, что в нулевом приближении энергия электронов системы

атомов равна энергии электрона изолированного атома Е

. При

сближении атомов (т. е. при учете взаимодействия электронов с ядрами

и электронами других атомов) уровни энергии опускаются на вели-

чину С и расщепляются в полосу некоторой ширины. Учитывая, что

Sp^O при ρ Φ 0, можно записать

£^=£

+ С + 2

е1

(кр)л

(Р)· (

30)

В качестве первого примера рассмотрим простую кубическую

решетку. Каждый атом имеет шесть ближайших атомов с координа-

тами

((1, 0, 0)

р = а (0, 1, 0)

1(0, О, 1)

100

(-1, 0, 0))

( 0, -1, 0) . (18.31)

( 0, 0, -l)j