Киреев П.С. Физика полупроводников

Подождите немного. Документ загружается.

Считая обменную энергию изотропной: Α (ρ) =

А(\

= А и пре-

небрегая обменом электронами с более удаленными атомами, получим

£(υ = Ε

+ С + 2A (cos к

а + cos к

а + cos κ

α) = Ε (к). (18.32)

Энергия зависит квазинепрерывно от волнового вектора к и

меняется в интервале от Е

т[п

до Е

тйХ

Таким образом, в результате взаимодействия атомов уровень

энергии изолированного атома Е

опускается на величину С и рас-

щепляется в полосу, или зону, шириной \2\A\ {для простой куби-

ческой решетки). Энергетические полосы разделены запрещенными

интервалами энергии— запрещенными зонами. Ширина энергетической

зоны зависит от величины обменной энергии А. Но обменная энер-

гия зависит от области перекрытия волновых функций— чем силь-

нее перекрываются волновые функции атомов, тем больше обменная

энергия. Отсюда следует, что уровни энергии внутренних электрон-

ных оболочек расщепляются меньше, чем наружных, поскольку элек-

троны внутренних оболочек локализованы в меньших по размеру

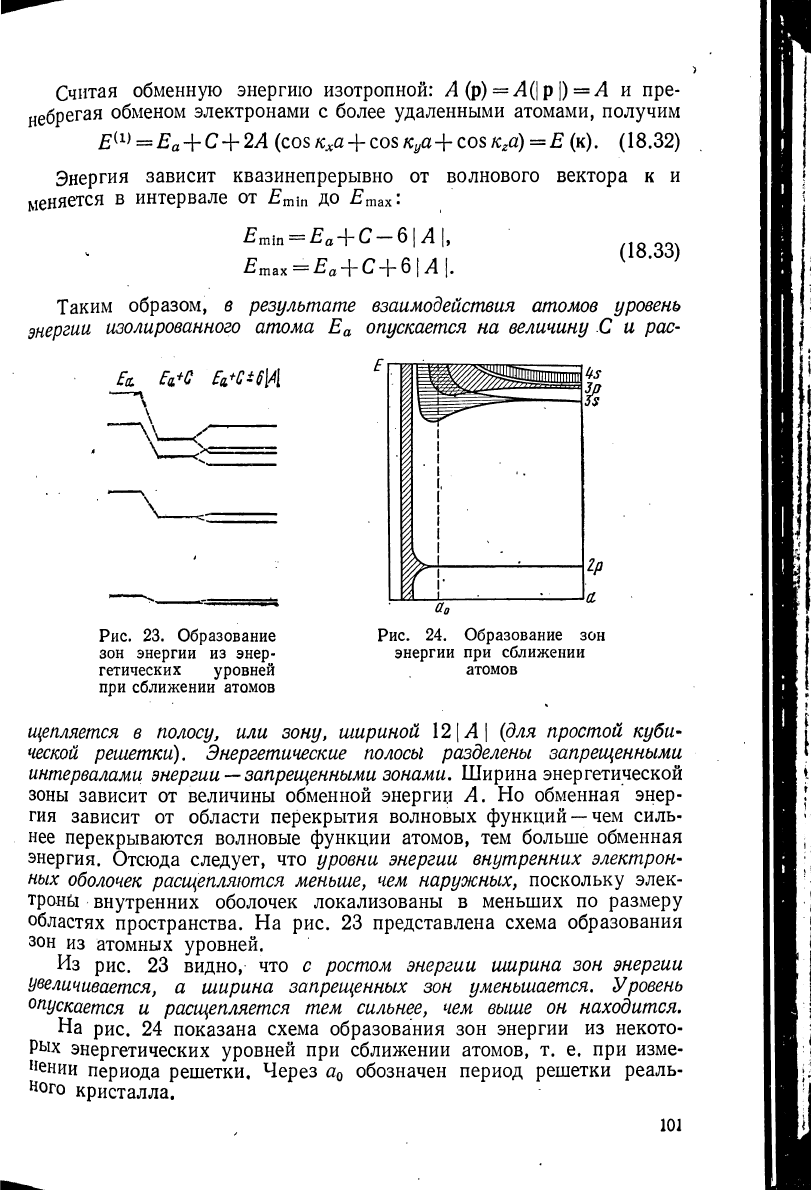
областях пространства. На рис. 23 представлена схема образования

зон из атомных уровней.

Из рис. 23 видно, что с ростом энергии ширина зон энергии

Увеличивается, а ширина запрещенных зон уменьшается. Уровень

Щскается и расщепляется тем сильнее

чем выше он находится.

На рис. 24 показана схема образования зон энергии из некото-

рых энергетических уровней при сближении атомов, т. е. при изме-

нении периода решетки. Через а

обозначен период решетки реаль-

ного кристалла.

щ = Е

+ С-6\А\

Етах = Е

+ С+6\А\.

(18.33)

Рис. 23. Образование

зон энергии из энер-

гетических уровней

при сближении атомов

Рис. 24. Образование зон

энергии при сближении

атомов

101

Для тетрагональной или ромбической кристаллических систем

расстояния между атомами в различных направлениях разные, по,

этому и обменный интеграл может зависеть от направления. Обозна*

чив координаты соседних атомов ρ в виде

(а

0, 0); (—а

(0, а* 0); (0, -й

(0, 0, а

); (0, 0,

(18.34)

и соответствующие этим направлениям обменные энергии через А

, А

> можем записать

Ε (к) = Ε

+ С + 2А

cos к

+ 2Л

cos к

+ 2А

cos κ

. (18.35)

Найдем экстремальные точки, полагая dE (ικ)/άκ = 0. Легко видеть,

что экстремумы энергии находятся в точках % = 0 и K

= ±n/a

т. е. в центре и вершинах зоны Бриллюэна.

Разлагая Ε (к) в ряд Тейлора относительно точек Kq, получим

в общем виде

Ε (К) = ^extr + у (

о)

· ·

или

о о

(18.36)

(18.37)

1=1

f=l

ЕЫ = Е

0 +

С-21А; + Ц^(

К1

±?:)

(18.38)

Для эффективной массы ш* имеем выражение

ш*

-1

= zt

; \

2Л

а|

ti* /

(18.39)

где минус соответствует точке к

= 0, а плюс —точкам (±η/αν

± я/я

; ± п/а

) = я (Ь

, Ь

Знак эффективной массы определяется знаком обменной энергии.

При Αι^> 0 в центре зоны Бриллюэна находится максимум энер-

гии, минимум энергии находится в вершинах зоны Бриллюэна. Пр

Л/ <С]

0 максимум энергии будет находиться в вершинах, а мини-

мум—в центре зоны Бриллюэна.

Энергия является действительно квадратичной функцией (к

— Ко)

и периодична с периодом 2π&, что непосредственно видно из анали-

тической зависимости Е{к).

102

Компоненты тензора эффективной массы в максимуме и мини-

муме отличаются только знаком, по модулю они равны. Другими

словами, форма изоэнергетических поверхностей в окрестности мак-

симума и минимума для одной и той же зоны одинакова. Компо-

ненты тензора эффективной массы обратно пропорциональны обмен-

ной энергии:

Щ = ± ^т; (18.40)

Так как обменная энергия определяет ширину зоны энергии, то

можно сказать, что эффективная масса обратно пропорциональна

ширине энергетической зоны. Это означает, что чем выше располо-

жена зона энергии, тем меньше в ней эффек-

тивная масса носителей заряда.

Изоэнергетические поверхности в окрестно-

сти экстремумов являются эллипсоидами, на-

пример, при Л*<0'(к

= 0)

' Й

/ к

. = + (18.41)

' а

JC_

Рис. 25. Связь. между

энергией и

волновым

вектором при

> 0 и

Л <0

Максимумов для этого случая будет восемь

в соответствии с числом вершин куба. Но так

как каждая изоэнергетическая поверхность,

построенная вокруг вершины куба, принадле-

жит первой зоне Бриллюэна на 1/8, то на пер-

вую зону приходится только один полный

эллипсоид энергии. Этот факт очень важен при

подсчете плотности состояний в зоне энергии.

Для простой кубической решетки обменная энергия изотропна:

Л(р) = Л(|р|), поэтому эффективная масса является скаляром

± НУ (2а

А). (18.42)

Изоэнергетические поверхности в окрестности экстремума явля-

ются сферами. На рис. 25 представлена графическая

зависимость

£ (к). Поверхности энергии имеют вид, который изображен на рис. 17.

Рассмотрим вопрос о ширине запрещенной зоны. Определим ши-

рину запрещенной зоны Af'o между п-й и (п+ 1)-й энергетическими

зонами как минимальное по энергии расстояние между ними:

A£'

= £

(M-|-i)min

—

Ε птах- (18.43)

Подставляя выражение (18.37) и (18.38) для экстремумов энер-

гии в

двух зонах, получим

Ea{n+l) + С (

Л+1

) — 221

1=1

*/(«+1)

+ C

+ 2^\A

ί=1

[Eatnw - En] -h [<Vi - С

] - 2 2 (I

Л/(л+1) I

+1 A

I). (18.44)

103

Этот результат очень нагляден. Будем для простоты считать,

Чт

+i^C

. В таком случае ширина запрещенной зоны меньше р

ас

стояния между уровнями Е

а{п+1)

—

ап

на сумму полуширин соседу

энергетических зон. Так как с ростом энергии расстояния «межд^

уровнями уменьшаются, а ширина зон энергии увеличивается,

ширина запрещенных зон с ростом энергии уменьшается. Этот резуд

ь>

тат является основой для объяснения зависимости ширины запр

щенной зоны от порядкового номера элементов одной и той ^

группы. Например, ширина запрещенной зоны, отделяющей валент,

ную зону от ближайшей свободной зоны для алмаза, кремния, гер*

мания и (серого) олова, должна уменьшаться в том же порядке

что соответствует экспериментальным данным.

Важное значение для объяснения многих явлений имеет знак

Αι двух соседних зон. Если Ац

п+1)

и A

имеют одинаковый знак,

то максимум и минимум энергии для этих зон находятся в различ-

ных точках зоны Бриллюэна (центре и вершинах зоны). Если же

1) и Ai

имеют разные знаки, то минимум и максимум нахо-

дятся соответственно в одних и тех же точках зоны Бриллюэна

(см. рис. 25). Каждой энергетической зоне соответствует своя зона

Бриллюэна, которые считаем как бы наложенными одна на

Другую.

Косинусоидальная зависимость энергии Ε от к для простой куби-

ческой решетки получена в результате учета обменной энергии

Л (1,0,0) только для ближайших атомов. Если учесть более уда-

ленные атомы, то выражение для Ε (к) усложняется, однако основ-

ные качественные выводы при этом сохраняются. Учтем обменную

энергию Л(1, 1, 0) с атомами, имеющими координаты а(

1, 0);

(1 , 0, 1) и т. д. Выражение для энергии будет при этом иметь вид

Ε (к) = Ε

+ С + 2А (1, 0, 0) (cos к

а + cos к

а + cos κ

α) +

+2А (1

\, 0) [cos (к

-\r

) аcos (к

— Ку)

а + cos (к

+ κ

) а +

+ cos (к

—

) а + cos (к

+ к

) а + cos (к

—

) а]. (18.45)

Если

А (110)

| |

А (100) то характер изоэнергетических поверх-

ностей изменится незначительно. Если же

А (100)

А (110)

то

изменения как в положении экстремумов, так и форме изоэнергети-

ческих поверхностей будут существенными.

Рассмотрим зависимость энергии от квазиимпульса для объемно-

центрированной решетки, учитывая взаимодействие только ближай-

ших соседних атомов. Если длину ребра куба обозначить через

а начало координат совместить с атомом, находящимся в центр

куба, то координаты атомов, лежащих в вершинах куба, равны

Р =

(

• 1);

(-1,

-1,-1)

1); ( 1,

-ι, -1)

2"'

(

1, -1,

1);

ι. - О

. (

-1);

(-1,

-ι. 1)

(18.46)

104

Подставляя (18.46) в (18.30), получим

(к)

= Е

+ С + 2 A [cos (к

+ к

)±+ cos (— к

+ к

)

-} - cos (к

Ку-\-

)

-Ц-

+cos{K

Ky —

)-^j =

(18.47)

™

км к

а κ

= Е

+ С + 8А cos-J- cos -γ cos-γ.

Как видно из выражения (18.47) для Е(к), экстремальные зна-

чения энергии определяются условием, что косинусы равны 1 по

модулю, и

Ет'т =Е

-\-С

—

А I,

£тах = £* + С + 8|Л|,

;

что дает "для ширины зоны энергии величину 16|Л|.

Если построить в пространстве к куб с ребром Απ/а, то в нем

будет находиться 27 экстремальных точек

—

в~ центре куба одна,

в центре граней шесть, в вершинах куба восемь и в середине ребер

двенадцать. Однако выделенный объем превосходит объем первой

зоны Бриллюэна, представляющий собой додекаэдр.

Найдем зависимость энергии от волно'вого вектора для гране-

центрированной решетки. Совмещая начало координат с атомом,

находящимся в вершине куба с ребром а, запишем координаты 12

ближайших соседних атомов:

( ι,

(-1, 1,0)

( 1,-1,0)

(-1, -1, 0)

( 1, О, 1)

( 1,0,-1)

(-1,0, 1)

(-1, о, -1)

(0, 1, 1)

(0, -1, 1)

(0, 1,-1)

(0, -1,-1)

(18.49)

Считая, как и прежде, обменную энергию изотропной, можем

записать:

Ε (к) = Ε

+ С + 2A [cos. (к

+ к

)^- + cos (к

- к

) у +

COS

(к

К,)

γ + cos (к

- К

) γ +

COS

(к

+ К

) + cos (к

)

yj =

с- , о , ,. л Г

αΚχ ак

У ,·

ак

ακ

ζ ,

ак

*Л

— Ε а + С + 4 A cos -γ cos -γ -f cos -γ cos -γ + cos —γ cos —γ I.

(18.50)

Предположим для определенности, что А > 0. В таком случае

Центре зоны Бриллюэна находится максимум энергии величиной

J-max. —

(18.51)

105

Минимум энергии не может быть равен Е

+ С

— \2А>

поскольку

для этого попарные произведения косинусов должны быть равны

—

что невозможно. Записав условия экстремума для (18.51), найдем

т = Еа + С-4А, (18.52)

т. е. ширина зоны энергии равна 161 А

а не 241 А

В заключение этого параграфа остановимся. на одном моменте

связанном с вырождением атомных уровлей. s-уровень энергии атома

является простым, все остальные уровни энергии вырожденные

фактор вырождения (без учета спина) равен при этом

= (2/ 1)]

где I

—

орбитальное квантовое число, поэтому р-уровии имеют трех!

кратное вырождение, d-уровни

—

пятикратное вырождение и т. д.

Благодаря взаимодействию орбитального и спинового магнитных

моментов электрона уровни энергии имеют так называемую тонкую

структуру .

Но если уровни энергии атома вырождены, то волновая функция

электрона в кристалле должна строиться

с учетом вырождения

атомных состояний:

Г (*)=Σ*

ί(Κη)<

ΜΡαα (Г- П), (18.53)

η, α

где с

—

неизвестный коэффициент, а принимает g различных зна-

чений. Подставляя (18.53) в (18.19), можно вычислить энергию Е.

Отличие последнего случая от рассмотренного ранее состоит в том,

что теперь интегралы, вычисленные с помощью различных атомных

волновых функций, будут различными. В результате этого вырож-

дение может быть частично или полностью снято, и для р-зоны

можно полунить три различные ветви энергии Ε {к).

Резюме § 18

1. В теории квазисвязанного электрона в качестве нулевого при-

ближения для гамйльтониана поля решетки принимается гамильто-

ниан электрона в изолированном атоме. Оператор возмущения пред-

ставляет собой энергию взаимодействия атомов друг с другом и энер-

гию электрона в поле всех остальных ядер. Волновая функция

электрона в кристалле представляет собой линейную комбинацию

атомных волновых функций, удовлетворяющую трансляционному

условию.

2. «Возмущение», т. е. взаимодействие электрона данного атома

со всеми ядрами и электронными оболочками, приводит к тому, что

уровни энергии Е

электрона в атоме существенно видоизменяются:

они опускаются вниз и расщепляются в полосу, или зону энергии.

3. Уровень Е

опускается тем сильнее, чем выше он расположен

в изолированном атоме, поскольку с ростом энергии Е

размерь*

электронного облака увеличиваются.

106

4. Если атомы кристалла сближать неограниченно, то начиная

некоторых расстояний между электронными оболочками атомов

возникнут силы отталкивания, потенциальная энергия W (г) станет

положительной, быстро возрастающей величиной, что приведет

к подъему уровня энергии £

(С>0).

5. Ширина зоны энергии пропорциональна обменному интегралу,

который возрастает с ростом Е

, поэтому чем выше расположена

зона энергии, тем она шире (см. рис. 23).

6. Ширина запрещенной зоны тем меньше, чем выше располо-

жены зоны энергии. Уменьшение ширины запрещенных зон с ростом

энергии обусловлено уменьшением расстояний между соответствую-

щими уровнями энергии и возрастанием ширины зоны энергии. При

больших значениях энергии зоны энергии могут накладываться,

перекрываться (см. рис. 23).

7. Эффективная масса электрона обратно пропорциональна обмен-

ному интегралу и тем самым ширине зоны энергии. Поскольку при

прочих равных условиях увеличение ширины зоны энергии приво-

дит к уменьшению ширины запрещенной зоны, можно ожидать, что

в веществах с меньшей шириной запрещенной зоны эффективная

масса электрона должна быть меньше.

8. Воздействия, приводящие к изменению расстояния между ато-

мами (нагрев, сжатие или растяжение), меняют область перекрытия

волновых функций, что приводит к изменению обменного интеграла,

благодаря чему меняется ширина зоны энергии, эффективная масса

и ширина запрещенных зон. Это в свою очередь приводит к изме-

нению физических свойств полупроводников, зависящих от ширины

запрещенной зоны или эффективной массы.

9. Зонная структура спектра энергии вытекает как из теории

квазисвободного, так и из теории квазисвязанного электрона. При

этом выводы первой теории применимы с большей точностью в области

больших энергий, а выводы второй теории оправдываются при малых

энергиях.

§ 19. МЕТОД ЭФФЕКТИВНОЙ МАССЫ. ВЛИЯНИЕ ВНЕШНИХ ПОЛЕЙ

НА СПЕКТР ЭНЕРГИИ КРИСТАЛЛА

Перейдем к рассмотрению решений уравнения Шредингера для

случая, когда на кристалл наложено внешнее поле V (г):

Ηψ = [- £ Δ + и (г) + V (г)] ψ (г) = (г). (19.1)

Чтобы решить это уравнение, необходимо знать поле U (г), кото-

Рое нам неизвестно. Однако существует удобный и достаточно точ-

ный метод решения уравнения (19.1), который получил название

метода эффективной массы. Чтобы понять его, рассмотрим вновь

Решение уравнения Шредингера для идеального кристалла. Как

известно, волновая функция электрона в идеальном кристалле пред-

107

ставляет собой функцию Блоха г(З

(г), а энергия электрона в окрест*

ности экстремума к

является квадратичной функцией квазиимпульса

или волнового вектора:

Йо^к

(Г)

= [- I; Δ + υ

(г)]

(г) = Ε

(κ)

(г);

EW^f^ + ^iK-Ko)

, (19.2)

Рассмотрим гамильтониан H

представляющий собой гамильтониан свободной частицы, масса кото-

рой совпадает с эффективной массой электрона. Решим уравнение

Шредингера

ΗοΨΟ

£ΟΨΟ.

(19.4)

. Подставляя вместо Н

его выражение, можем записать

+ = (19.5)

Непосредственной подстановкой

ψο

= Ae

i{aX+

(19.6)

в это уравнение можно убедиться, что ψ

является решением урав-

нения (19.4) и (19.5), причем

Сравнивая (19.7) с (19.2), приходим к выводу, что уравнение

(19.4) имеет тот же спектр энергии, что и уравнение (19.2), если

выбрать α, β, γ в виде

а = к

—

0х

; $ = Ку-гК

оу

; у = к

—

οζ

, (19.8)

а начало отсчета энергии совместить с точкой экстремума, т. е.

положить Ε (к

) = 0. В общем случае гамильтониан

= -^1д + £(ко) (19.9)

имеет тот же спектр энергии, что и гамильтониан поля решетки

в окрестности экстремума, а его собственные волновые функции

имеют вид

гро

(г) = —1=

е'

(к

°· г)

(19.Ю)

Таким образом, движение частицы в кристалле подобно движению

свободной частицы. Различие между действительно свободной части-

108

ней и частицей в кристалле заложено б различиях масс: вместо

массы свободной частицы необходимо использовать эффективную

массу ш*.

При наложении внешних полей V (г) уравнение Шредингера

(19.1) может быть записано в виде

[- Δ+ V (Γ)]ψ (г) = £ψ (г). (19.11)

Реши в это уравнение,, найдем волновую функцию ψ (г) и значе-

ние энергии Ε электрона в кристалле, находящемся во внешнем

поле. Решение задач на основе уравнения (19.11) получило название

метода эффективной массы. Его преимуществом по сравнению с общим

уравнением (19.1) является то, что вместо неизвестного поля

решетки U (г) мы можем воспользоваться экспериментально опреде-

ленной эффективной массой т* частицы. Недостатком его является

приближенный характер, поскольку оно имеет смысл лишь для

состояний в окрестности экстремумов.

Используя функции Ванье, можно показать более строго, что

уравнение (19.1) не приводит к существенному изменению спектра

энергии в плавно меняющихся внешних полях, а волновая функция

действительно имеет вид (19.10).

Чтобы найти изменения, возникающие в спектре энергии идеаль-

ного кристалла под действием внешнего поля, воспользуемся не

обычной теорией возмущений, а квантовым уравнением движения.

Рассмотрим гамильтониан кристалла во внешнем поле (19.1). Кван-

товое уравнение движения для произвольной, не зависящей явно от

времени физической величины с оператором L, имеет вид

^-[ft, L] = 1(LH-HL). (19.12)

Применим это уравнение для гамильтониана идеального кристалла

^ =

]

[V, Н

] == [V,

t]=4(-£){AV-VA}-

2т

{

AV) + 2(W, V)}. (19.13)

Остановимся на полях, слабо меняющихся в пространстве; для

них величиной AV можно пренебречь по сравнению со вторым ела*

аемым. Учитывая, что (VV) = — F

, а

= i = (19.14)

т т dt

9 4

запишем

(19.15)

109

Усредним это выражение по исходным состояниям с волновой

функцией ΨΚ(Γ), Предполагая, что F

не зависит от координаты,

можем вынести F

из-под знака интеграла:

/<Шо\ d £ * /

л .. /

, __ (к)

d i

Ψί (r) (F

v) ψ« (Γ) dx = (F

<ν». (19.16)

Уравнение (19.16) является классическим, и оно показывает,

что «полная» энергия Е

(к) меняется со временем в результате работы

внешней силы F

. Его можно получить из уравнения движения

dP/dt = F

= —

V V\

(19.17)

Умножим (19.17) на скорость v — dr/dt:

(ν S) г -

i^p-(,™--

Г Г--f. О··"»

или

(Ρ) + V (г) = #0 (Ρ, г) = const. , (19.19)

Через Η

(Ρ, г) мы обозначили сохраняющуюся во времени функ-

цию Гамильтона электрона в кристалле, на который наложено

внешнее потенциальное поле V(r).. Уравнению (19.19) как раз и

соответствует уравнение (19.11), благодаря чему метод эффективной

массы получает строгое квантовомеханическое обоснование.

Обратим внимание, что при движении частицы в кристалле под

действием внешнего поля его полная энергия Н

сохраняется,

в то время как Е

(Р) и V (г) меняются, причем в противополож-

ных направлениях. Но если V (г) может меняться в любых преде-

лах, то Е

(Р) может меняться только в пределах зоны энергии:

от fmin до Ε max. Но отсюда вытекает, что изменение V (г) ограни-

чено тем же интервалом; действительно, возьмем дифференциалы

от левой и правой частей уравнения (19.19), получим

+ dV = 0, или 6E

+ 6V = 0. (19.20),

Полагая 8E

= E

max

—E

in, получим

β =

.—

§Е

о —

Ε mm Ε

щах ·

(19.21)

Из (19.21) также вытекает, что в однородном электрическом

поле электрон должен совершать колебательное периодическое дви-

жение вдоль поля на участке длиной

bV = - (6rF

) = - (£тах - £min), (19.22)

откуда

Ρ г ρ ρ

fif— max min max ^min (19 23)

110