Киреев П.С. Физика полупроводников
Подождите немного. Документ загружается.


Положение уровня энергии E
t
указано с плюсом, если E
t
отсчитывается от Ε
ν
, и с минусом, если E
t
отсчитывается от Е
с
.
Для сравнения приведена вероятность захвата электронов атомом
галлия.
Резюме § 65
1. Дефект, способный захватывать свободные носители заряда
с последующим их освобождением, называется ловушкой захвата.
2. Дефект, способный захватывать последовательно электрон и
дырку, что приводит к рекомбинации пары свободных носителей
заряда, называется рекомбинационной ловушкой.
3. Теория рекомбинации электронов и дырок через рекомбина-
ционные ловушки приводит к следующему выражению для времени
жизни пары τ = x
f
\
которое описывает зависимость времени жизни пары:
а) от величины избыточной концентрации неравновесных носи-
телей заряда δη = δρ (от уровня инжекции); б) от равновесной кон-
центрации носителей заряда п
0
, р
0
; в) от положения уровня энер-
гии E
t
рекомбинационной ловушки (посредством п
г
и р
г
); г) от
концентрации дефектов N
t
и вероятности захвата (с
п
) и <с
р
)
у
опре-
деляющих время захвата τ
η0
и τ
ρ0
.'
4. При малом уровне инжекции в области примесной проводи-
мости время жизни пары определяется временем захвата неоснов-
ных носителей заряда. По мере перемещения уровня Ферми к сере-
дине запрещенной зоны время жизни пары возрастает.
5. Для описания неравновесных состояний может быть исполь-
зована функция Ферми
—
Дирака, параметры которой должны быть
изменены. Если верхние уровни заселены больше, чем нижние, то
температуру системы неравновесных частиц необходимо считать вели-
чиной отрицательной: Г< 0. Такие системы называются системами
с инверсной населенностью уровней, или системами с отрицательной
температурой; они используются для создания квантовых генерато-
ров и усилителей.
Если распределение неравновесных частиц по уровням энергии
нормальное, то такая система описывается квазиуровнем Ферми У
7
*,
определяемым из условия нормировки неравновесной функции рас-
пределения на неравновесную концентрацию η:
η=ΆΦι (ξ*). (65.2ρ)
Κπ 2
Для невырожденных полупроводников положение квазиуровня
Ферми можно определить из уравнений для электронов
nz=NcQ
-^kT
J1
. F% = E
c
^kT\n^-, (65. Зр)
441.

для дырок
p = N
v
e
kT
;
—
E
v
—
kT
\n
. (65.4p)
Расстояние между , квазиуровнями электронов и дырок опреде-
ляется уровнем инжекции:
F% —
Fp = kT In — = £7 ln^. (65.5р)
п
0
р
0
n
t
Для вырожденных полупроводников связь между неравновесной
концентрацией и квазиуровнем Ферми можно получить, учитывая,
что
ΦΙ/2(Γ) = 4^
3/2
.
§ 66. ДИФФУЗИЯ И ДРЕЙФ НЕРАВНОВЕСНЫХ НОСИТЕЛЕЙ ЗАРЯДА
Если в полупроводниках создать неравновесные носители заряда,
то в них наблюдается целый ряд новых физических явлений. Они
могут быть описаны на основе обобщенного кинетического уравнения
Больцмана или с помощью вытекающего из него уравнения непре-
рывности:
|=-div| + G-R. ·' (66.1)
Рассмотрим стационарное состояние в отсутствие генерации носи-
телей заряда за. счет внешней энергии, т. е. положим dn/dt = О,
(3 = 0, после чего уравнение <66.1) запишем в виде
. ydivj + R = 0. (66.2)
Из уравнения (66.2) следует, что при R^=0 неравновесная кон-
центрация носителей заряда поддерживается током j. Другими сло-
вами, уменьшение избыточной концентрации носителей заряда вслед-
ствие рекомбинации компенсируется расходимостью тока.
Для величины плотности тока j мы можем воспользоваться
общим выражением (38.1 р), считая, что кинетические коэффициенты
выражаются через неравновесную концентрацию η и усредненное
время релаксации для неравновесных носителей заряда. Будем
считать, что магнитное поле отсутствует (В = 0), полупроводник
находится в изотермических условиях (V7
1
= 0). В таком случае из
(38.1р) запишем
j =
£
2
/СЦЕ —
eK
n
VF*. (66.3)
Необходимость сохранения члена
—
eKnVF* очевидна, если
учесть, что он описывает ток, обусловленный неоднородностью полу;
проводника. В данном случае неоднородность вызывается возможной
442.

зависимостью неравновесной концентрации носителей заряда от коор-
динаты. Перепишем уравнение (66.3), учитывая выражения для /Си·'
j=e
2
пЩ-Е-епЩ V/
7
* = σΕ - ημ^*. (66.4)
• ''^ 171
Из (65.3р) можем записать для невырожденного полупроводника
VF*=kT~, (66.5)
откуда
j = dE-^Vtt==jE + b, (66.6)
где. jE = aE представляет собой омический, или дрейфовый, ток, а
j
D
= —A7>
rf
V/i (66.7)
носит название диффузионного тока. Последнее название связано с тем,
что ток j о возникает вследствие диффузии носителей заряда при их
неравномерном распределении в кристалле. Поток частиц должен
быть пропорционален градиенту "концентрации и направлен в сто-
рону уменьшения концентрации частиц. Умножая поток частиц на
их заряд и вводя коэффициент пропорциональности D, можем запи-
сать
]d = — eDln. (66.8)
Величину D называют коэффициентом диффузии, он имеет раз-
мерность [L
2
7
_1
], как это видно из его определения соотношением
(66.8). Сравнивая (66.8) с (66.7), получим связь между коэффи-
циентом диффузии и подвижностью носителей заряда
0 = (66.9)
— выражение, справедливое как для дырок, так и для электронов.
Выражение (66.9) называется соотношением Эйнштейна для подвиж-
ности и коэффициента диффузии. Подобное же соотношение можно
получить и для вырожденного полупроводника. Действительно, учи-
тывая связь между я и Ζ
7
*, получим
-Ι'·?'··'· «*·'°>
откуда
Подставим уравнение (66.6) для j в (66.2), получим
-idiv(aE-eDVn) =0, (66.12)
или
ημ
α
div Ε (EVn) - DV
2
n + = o. (66.13)
443.

Выражение (66.13) может быть записано как для дырок, так и
для электронов, при этом величина электрического поля, входя-
щего в уравнение (66.13) для электронов и дырок, не зависит от
знака заряда частиц. Поскольку при прохождении тока электро-
нейтральность не нарушается, то на основании уравнения Пуас-
сона можем записать
divE = 0, (66.14)
после чего уравнение (66.13) примет вид
= - (65.15)
Так как неравновесная концентрация поддерживается током, то
Vn должен быть коллинеарен Е. Рассмотрим одномерный случай,
положив Е = (Е, 0, 0),_и запишем уравнение (66.15) для избыточной
концентрации п
—
п
0
:
d*(n—n
0
) μ
ά
Ε d (η—η
0
) η—η
0 Λ
—Ш D Τχ
Dx~
=
(
66Л6
)
Введем обозначения
Dx = L
2
,
μ
α
Ε μ
α
Ετ l
E
В новых обозначениях уравнение (66.16) будет иметь вид
d
2
(η /г
0
) · l
E
d(n-n
0
) п
— п
0
L? dx ΰ~
=
(
66Л8
)
Ищем решение линейного однородного уравнения в виде
п
—
п
0
= Ае
ах
. (66; 19)
Подставив (66.20) в (66.19), после сокращения на Ае
ах
получим
характеристическое уравнение
= \ (66.20)
решение которого имеет вид
Введем величину
/
= — 1 /а, с помощью которой запишем решение
(66.19):
я-По^е-*/'. (66.22)
Чтобы решение было конечным при необходимо выбрать
а < 0 или
/
> 0, А имеет смысл избыточной концентрации в точке
444.

χ = 0: [я
—
п
0
]\
х
=
о
= А. Из условия а<О следует, что в (66.21)
необходимо оставить знак минус перед корнем, поэтому .
τ = t(V
1
+^-W)· <
66
·
23
>
Мы пришли к выводу, что избыточная концентрация с ростом χ
уменьшается по экспоненте с некоторой характеристической вели-
чиной I, которую называют длиной затягивания; она равна расстоя-
нию, на котором избыточная концентрация уменьшается в е раз.
Рассмотрим случай, когда электрического поля нет: Ε = 0. В
таком случае /
Е
= 0 и .
/
= L^V
r
Px. (66.24)
В вещестре нет электрического поля, в нем течет лишь диффу-
зионный ток
j = j
D
= — eDVn. (66.25)
Так как избыточная концентрация изменяется только в резуль-
тате диффузии неравновесных носителей заряда, то l = L называется
диффузионной длиной. Для одномерного случая
χ
η
(χ)
- п
0
= δη
(χ)
= δη
(0)
e
L
(66.26)
и ' .
j = — = = = (66.27)
Обозначим отношение L/τ через v
D
:
υ
°~ Τ
=
Т?
=
Τ"' (
66
·
2
5)
Величину Vd называют диффузионной скоростью, она равна чис-
ленно скорости, с которой неравновесные носители заряда проходят
путь, равный диффузионной длине, за время их жизни. Плотность
диффузионного тока можно выразить через диффузионную скорость:
jDx=eu
D
(n-n
0
) = j
DO
e-
x
/
L
. (66.29)
Выражение (66.29) показывает, что плотность диффузионного
тока уменьшается по тому же закону, по которому изменяется
избыточная концентрация, уменьшение которой обусловлено реком-
бинацией неравновесных носителей заряда. Выражения (66.24
—
29)
будут справедливы не только при Е = 0, но и при Е^О, если
IE<2L. .
Рассмотрим противоположный случай
—
случай больших полей:
/|^>4/А Это условие имеет наглядный смысл:
4^2 =
β
Щ>
1
' (
66
·
30)
445.
Величина I Ε численно равна пути, который проходят неравновес-
ные частицы за время жизни со скоростью дрейфа
у
поэтому ее назы-
вают длиной дрейфа неравновесных носителей заряда. Таким образом,
поле Ε будем считать большим, если длина дрейфа намного превос-
ходит диффузионную длину. Однако при нахождении длины затяги-
вания I надо различать два случая /Е>0 И /Е<0. Рассмотрим
случай /
Е
> 0, из (66.23) можем записать
1
-Ι^ΐΛ 4-iii'-AUMl-l·- —+
I ~~ L \2L V
1
2L) 2L
2
\
/|
1
т. е.
/
=
—
длина затягивания равна длине дрейфа:
/
=
/
Е
= μ^Ετ = ν
α
τ (/
Е
> 0).
'г» <
66
·
31
)
(66.32)
Учитывая (66.22) и (66.32), запишем для избыточной концентра-
ции δ/ζ (л:): ч
бл(*) = бл(0)е
/Е
=бп(0)е
μ
"
Ε
\ (66.33)
Смысл этого выражения состоит в следующем. Если в начале
координат создается избыточная концентрация δη(0), то в результате
прохождения тока, вызываемого сильным электрическим полем, избы-
точная концентрация «затягивается» полем на расстояния (2-5-3)/Е
в объем полупроводника. Если при этом δη(0)>0, то объем обога-
щается неравновесными носителями зарядов; это явление называется
инжекцией неравновесных носителей заряда. Инжекция дырок в
точки χ > 0 из точки χ = 0 наблюдается
при Е>0, инжекция электронов
—
при
Е<0. Если избыточная концентрация
отрицательна
—
бя(0) < 0
—
, то объем
обедняется носителями заряда, это яв-
ление называется экстракцией.,
Рассмотрим случай /
Е
<0, (|/Е|>0)·
Для длины затягивания I из (66.23)
получим
1 _ 4<EI
2
_I'E|. ,JL
Г66 34)
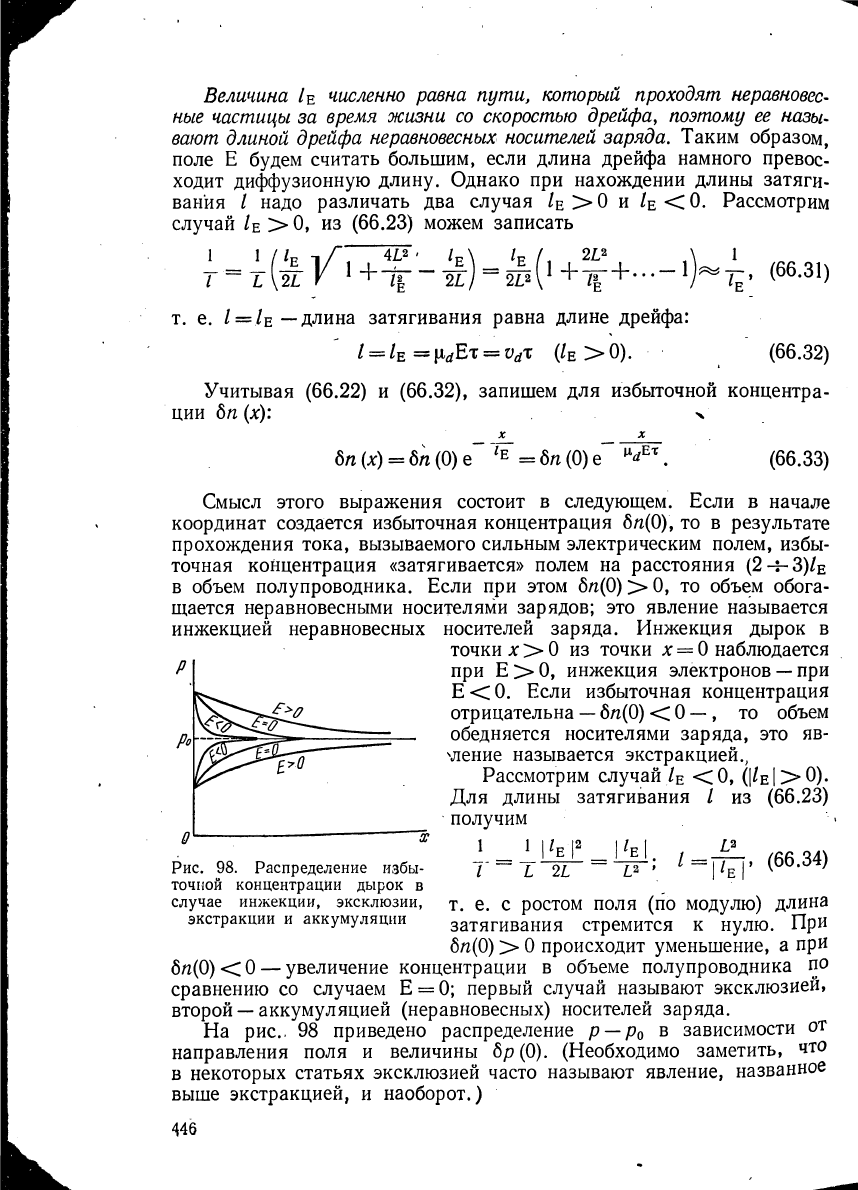
0
Рис. 98. Распределение избы-
точной концентрации дырок в
случае инжекции, эксклюзии,
экстракции и аккумуляции
т. е. с ростом поля (по модулю) длина
затягивания стремится к нулю. При
δη(0) > 0 происходит уменьшение, а при
блг(0) < 0 — увеличение концентрации в объеме полупроводника по
сравнению со случаем Е = 0; первый случай называют эксклюзией,
второй
—
аккумуляцией (неравновесных) носителей заряда.
На рис., 98 приведено распределение р
—
р
0
в зависимости от
направления поля и величины δρ(0). (Необходимо заметить, что
в некоторых статьях эксклюзией часто называют явление, названное
выше экстракцией, и наоборот.)
446.

Говоря об изменении избыточной концентрации носителей за-
ряда, мы не связывали его с видом частиц. Более того, условием
divE = 0 мы по существу предположили, что избыточные концен-
трации электронов и дырок меняются одинаковым образом. Чтобы
доказать это, рассмотрим полупроводник, в котором каким-либо
образом создан объемный заряд с плотностью ρ (г, 0). Введенный
заряд порождает электрическое поле Ε (г, /), которое связано с
Ρ (
г
> 0 уравнением Пуассона:
divE=£. (66.35)
εε
0
Электрическое поле Ε вызывает ток проводимости ]'Е=ОЕ. Из
уравнения непрерывности
- |=-divj (66.36)
следует
' — = — divaE = — σ div Е = —— = (66.37)
dt εε
0
τ
где через τ
Μ
обозначена величина, имеющая размерность времени:
(66.38)
Уравнение (66.37) решается элементарно:
ρ (г, ί) = ρ (г, 0) е
τΜ
. ' (66.39)
Оценим величину τ
Μ
, положив ε =10 и σ= 10 Сим-м
-1
и учи-
тывая, что ε
0
= 10
7
/4яс
2
= 8,85416· 10~
12
Ф/м, получим т^^10-
п
с.
Величину τ
Μ
называют временем релаксации Максвелла, она опреде-
ляется удельной электрической проводимостью вещества. Таким
образом, в результате проводимости объемный заряд, введенный в
полупроводник, существует в среднем в течение времени τ
Μ
. Но
отсюда вытекает важнейший для понимания многих вопросов физики
полупроводников и полупроводниковых приборов, связанных с нерав-
новесными носителями заряда, вывод: если создать в полупроводнике
избыточную концентрацию основных носителей заряда, то объемный
заряд и избыточная проводимость исчезнут в среднем через т
м
; но
если создать избыточную концентрацию неосновных носителей заряда,
то благодаря релаксации Максвелла их объемный заряд будет ском-
пенсирован основными носителями заряда через τ
Μ
, а избыточная
концентрация неосновных и основных носителей заряда будет сущест-
вовать в течение времени жизни jf неравновесных носителей заряда.
Таким образом, неосновные и основные неравновесные носители
заряда играют принципиально различную роль в изменении физи-
ческих свойств полупроводника, поэтому обычно говорят об инжек-
ции или экстракции только неосновных носителей заряда.
447.

Неизменность первоначального распределения объемного заряда
с течением времени, вытекающая из уравнения (66.39), возникает
потому, что мы учли только ток проводимости. В действительности
же будет иметь место диффузия заряда, поэтому объемный заряд
вследствие диффузии меняет свое распределение в кристалле.
Резюме §66 —
1. Рассасывание (или компенсация)-объемного заряда вследствие
проврдимости называется релаксацией Максвелла. Время релакса-
ции Максвелла определяется проводимостью вещества
в СИ в системе Гаусса
^(
66Л
р)
2. Избыточная концентрация основных носителей заряда рас-
сасывается через τ
Μ
; избыточная концентрация неосновных носите-
лей заряда исчезает вместе с вызываемой ею избыточной концентра-
цией основных носителей заряда через время жизни т^.
3. Изменение концентрации неравновесных неосновных носи-
телей заряда в стационарных условиях в отсутствие генерации
носителей заряда за счет энергии, попадающей извне, описывается
уравнением
±divj+^ = 0. (66.2р)
4. Ток в изотермических условиях и при В = 0 имеет вид
j = е
2
КцЕ - eKn^F* = j
E
+ Ь, (бб.Зр)
где
j
E
= е
2
КцЕ = βημ
α
Ε (66.4р)
есть ток проводимости, а
)
D
= — ημ^ν/
7
* = — еКи V/
7
* = — eDVn (66.5р)
есть диффузионный ток.
5. Коэффициент диффузии D и подвижность носителей заряда
связаны соотношением Эйнштейна:
D
n
= ~
μάη\
D
p = r № ι(66.6ρ)
t>n Cp
D
«=P
n
V«n>
D
P = lS;V<iP (66.7p)
соответственно для. невырожденного и вырожденного полупровод-
ников. ,
447.

6. Избыточная концентрация' неосновных носителей заряда в
одномерном случае определяется уравнением
х_
δη(χ) = δη( 0)е
1
\ (66.8р)
где / называется длиной затягивания; она связана с диффузионной
длиной L = YDxj и длиной дрейфа /Е =μ
ί
/Ετ
/
соотношением (66.23).
В слабом электрическом поле распределение, избыточной концентра-
ции неосновных носителей заряда определяется диффузией, в силь-
ном
—
дрейфом.
§ 67. ПОВЕРХНОСТНАЯ РЕКОМБИНАЦИЯ
На поверхности полупроводника содержится ряд дефектов, игра-
ющих роль рекомбинационных ловушек, что приводит к поверхност-
ной рекомбинации, уменьшающей концентрацию неравновесных
носителей заряда в приповерхностном слое полупроводника. Если
поверхность одного и того же полупроводника обработать различ-
ным образом, Например, шли-
фовкой, полировкой, травле-
нием, нанесением поверхност-
ного покрытия, то время
жизни, измеренное экспери-
Л
ментально, будет различным,
/
оно зависит от способа обра-
ботки поверхности. Наличие
поверхностной рекомбинации
можно наблюдать визуально
или с помощью электронно-
оптического преобразователя.
На рис. 99 приведена фото-
графия диода из арсенида
галлия, в котором инжекция р
ис<9
9. Свечение на поверхности диода из
создается большими импуль- арсенида галлия вследствие поверхностной
сами тока. Из рис. 99 видно, рекомбинации
что приповерхностные слои
образца светятся, в то время как объем остается темным (за исклю-
чением р-я-перехода, где возникает стимулированная рекомбинация).
Поверхностная рекомбинация обычно характеризуется так называв-
мой скоростью поверхностной рекомбинации s, которую можно
ввести следующим образом.
Запишем уравнение непрерывности в виде
£-_±divj-»-=b + a, (67.1)
которое мы решали выше в одномерном случае в предположении
неограниченности полупроводника вдоль осей у и ζ и G = 0. Учтем
15 Кирееа
449

наличие границ у полупроводника. Внешнее электрическое поле,
направленное вдоль оси образца (осьх), обеспечивает инжекцию
неосновных носителей заряда. Чтобы упростить уравнение (67.1),
будем считать, что электрическое поле отсутствует: Е = 0, а избы-
точная концентрация создается некоторым источником, дающим
независящую от координаты скорость генерации носителей заряда G.
В этом случае электрическое поле всюду будет равно нулю. Если
рассмотреть неограниченную вдоль оси у (и х) пластину, то урав-
нение непрерывности снова будет одномерным. Так как на поверх-
ности образца существует рекомбинация, то концентрация избыточ-
ных носителей заряда у поверхности должна быть меньше, чем в
объеме, вдали от поверхности. Наличие градиента концентрации
неравновесных носителей заряда должно создать диффузионный
поток, направленный из объема полупроводника к его поверхности.
Величина тока будет тем больше, чем больше происходит ' актов
рекомбинации и чем ближе к поверхности находится элемент объема,
в котором мы рассматриваем ток. Ток должен обращаться в нуль
на поверхности. Пусть величина рекомбинационного тока на поверх-
ности равна Уравнение непрерывности (67.1) в стационарных
условиях может быть записано в виде
0 = —idivj—^ + ' (67.2)
Подставляя вместо j величину —eDl
z
n> получим
или
+ (67.4)
Общее решение однородного уравнения имеет вид
ζ ζ
бп(г) = п(г)-п
0
= Ле~
т
+£е
т
. ' (
67
*
5
>
Частное решение неоднородного уравнения (67.3) можно выбрать
следующим образом:
δη = Gr
f
. (67.6)
Общее решение неоднородного уравнения равно их сумме:
δη (ζ) = Gx,[l - Л V ^ - В'е\|, (
67
·
7
)
где
450.
