Киреев П.С. Физика полупроводников

Подождите немного. Документ загружается.

Из соображений симметрии или из уравнения

= 0; _i —

Uq,

-|-ι = — и

следует, что Л

1 = Л

, -ι и Л

= 2Л

1, поэтому

1 - к

ω = ω

—

cos Κα)

= ω

Υ2 sin^.

При малых К фазовая скорость

sin

Κα

= ^ =

и групповая скорость

άω У 2

(59.34)

(59.35)

(59.36)

(59.37)

т. е. групповая скорость совпадает с фазовой скоростью. Выраже-

нию для

Уф

= У

гр

можно придать некоторый наглядный смысл. Обо-

значим через Т

—

среднее «натя-

жение» линейной цепочки и через

= —— среднюю плотность вещества;

в таком случае для скорости волн можем

записать выражение

= ^ = = (59-38)

Оно совпадает с выражением для

скорости упругих волн, или скорости

звука.

Таким образом, при К-+0 имеем ра-

венство ν

Γν

= ν

= с, где с— скорость

упругих волн, или скорость звука.

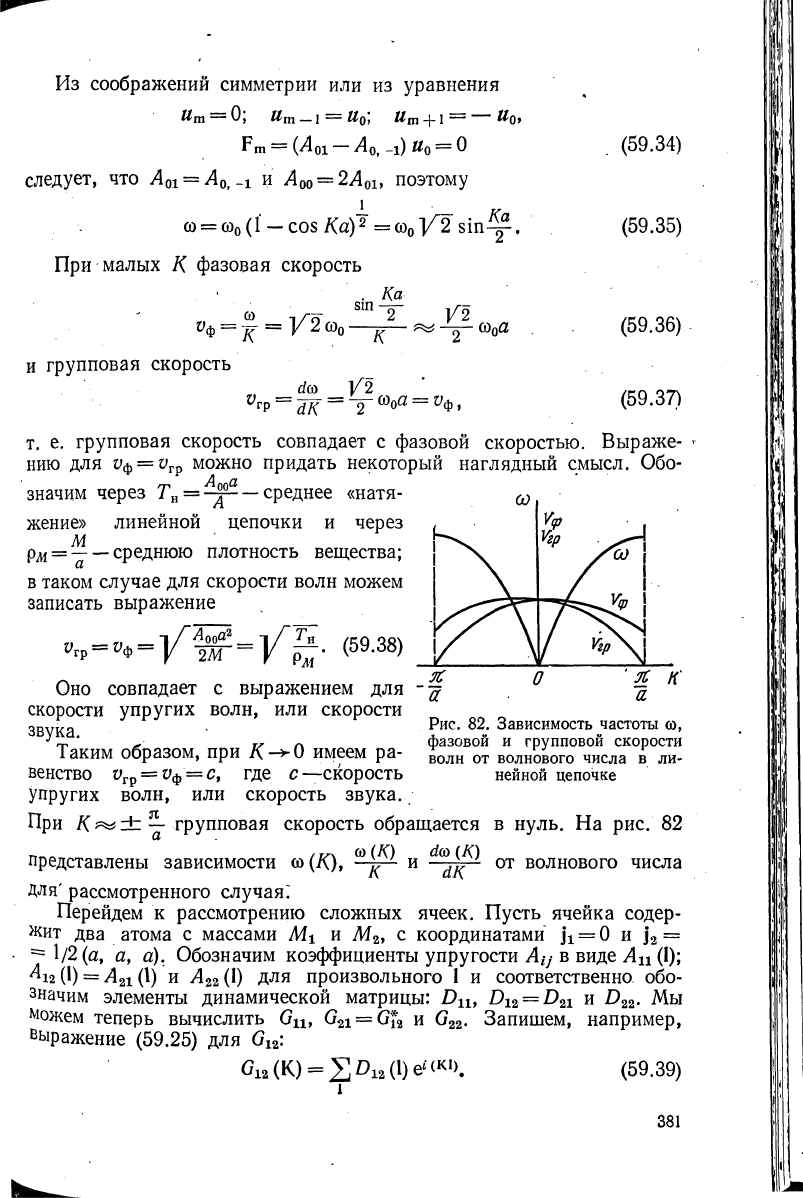
При К ± ~ групповая скорость обращается в нуль. На рис. 82

ι ω

(/О

d(0(K)

представлены зависимости ω(Λ), —^ и ^ от волнового числа

Для' рассмотренного случая;

Перейдем к рассмотрению сложных ячеек. Пусть ячейка содер-

жит два атома с массами Λίχ и М

, с координатами ji =

и j

- 1/2 (α, а, а). Обозначим коэффициенты упругости Ац в виде Ац (1);

^12 (1) = Α

ι (1) и Л

( 1) для произвольного 1 и соответственно обо-

значим элементы динамической матрицы: D

, D

= D

и D

. Мы

Можем теперь вычислить G

llf

= G?

и G

. Запишем, например,

Сражение (59.25) для G

Οΐ2(Κ) = Σ°ΐ2(

(Κ1

>. (59.39)

Рис. 82. Зависимость частоты ω,

фазовой и групповой скорости

волн от волнового числа в ли-

нейной цепочке

381

Составим детерминант (59.27):

= 0. (59.40)

Gn-ω

2l G

— (

Из (59.40) найдем ω

(in - ω

) (G

- ω

) - G

= 0, (59.41)

или

со*

со

+ G

) + G

- G

= 0. (59.42)

Решая уравнение (59.42), получим

^π4^22.

-|/· (On + g

)

0ц0и + Gi2

2i a

= +

(59.43)

т. e. ω

принимает два различных значения для каждого К.

Пусть, например, G

= G

, тогда

©ι —Gii +

|, (59.44)

Ι = Gn

— I

1. (59.45)

Перепишем систему уравнений (59.26) в следующем виде, опустив

нижние значки 0 и α у w§j,

—

) wj + G

W2 =

(59.46)

G21W1

+ (G

— ω

) w!j

= 0.

Так как ω

имеет два различных значения cof и ωто, подстав-

ляя их поочередно в (59.46), получим две системы уравнений:

при CDJ = GH + |G

4Gu|wi + G

w5 = 0,.l

wJ-|G

|wS = 0;J

при ωΐ = G

— I

|Gi

|wj+G

w§ = o, \

5948)

G12W1

I W

= 0. J

Из (59.47) следует, что если co

= G

1, то

,., Ο ι 012 .,.0

Из (59.48) аналогично следует, что при ω

= Gn

— |

..,ο ^12 ...о

IGul

382

(59.49)

(59.50)

Предположим, что б

величина действительная й положительная.

В таком случае имеем два типа колебаний

wj = wj (тип Л), (59.51)

° = —

w°

(тип О). (59.52)

Колебания типа Ά означают, что смещения обоих атомов одина-

ковы, ячейка смещается как одно целое. Это приводит к локальным

сжатиям и разрежениям в кристалле подобно сжатиям и разреже-

ниям, возникающим при прохождении упругих, или акустических,

волн, поэтому колебания, при котарых оба атома колеблются в фазе,

называются акустическими.

Колебания типа О означают, что атомы смещаются в противо-

положных направлениях, они колеблются в противофазе, поэтому

оставляют центр масс ячейки в покое, но зато в такой ячейке воз-

никает смещение центров тяжести зарядов, и в ячейке возникает

дипольный электрический момент. Так как при прохождении электро-

магнитной волны наблюдается сильное .взаимодействие света с коле-

баниями типа О, то они получили название оптических колебаний.

В общем случае G

может быть комплексной величиной, поэтому

представим ее в виде

^12 = 10ΐ21

» (59.53)

после чего уравнения (59.49) и (59.50) соответственно примут вид

= (59.54)

wj = —

PwS

= ё

t(p+3t)

w2. (59.55)

Если φ = π/2, то между типами колебаний А и О различие

теряется, поскольку и в том и в другом случае сдвиг фаз состав-

ляет ± π/2.

Чем ближе φ к 0 или π, тем отчетливее проявляется различие

между акустическими и оптическими колебаниями решетки, т. е.

тем сильнее изменяется распределение заряда или массы в ячейке.

Рассмотри м более общий случай, когда G

Φ G

. Подставляя

(59.46) вместо ω

значение из (59.43), получим два уравнения,

связывающих wj и

o<»

|βιι + β«

Gi2

]2|_L

o.I>

(59<56)

• и

oс

|<?

_ y + ήgL wj

(2Ϊ

, (59.57)

соответствующие плюсу и минусу перед корнем в (59.43). Так же,

Как и в частном случае G

= G

, одно решение соответствует син-

фазному колебанию атомов ячейки, второе решение

—

противофазному

383

колебанию, другими словами, акустической и оптической ветвям

колебаний. Рассмотрим зависимость ω (К) для оптической и акусти-

ческой ветвей в области малых К (длинных волн).

Чтоб ы получить зависимость ω (К), необходимо при вычислении

Gij взять, кроме

= 0, члены с 1=^0. Рассмотрим для простоты

одномерную цепочку атомов. Ограничимся простейшим случаем —

учтём взаимодействие только соседних атомов, т. е. будем считать,

что отличными от нуля являются Ац (0); А

(0); А

(0); Α

ι (0); А

(1)|

Л21 (1). Для простоты предположим, что Ли (0) = Л

(0) = Л; Л

(0) =

= Л

(0) =Л1

(1) = Л

(1) = Б. Между Л и β имеется определенная

связь; так как

(1)

= An (0) +

(0) +

Л12

(1) = Л + 2В = 0,

ι. j

то

Л = — 2В.

Вычислим Gij:

'12 "

Лц (0) , Л

(1)

Ум

1·

УЖЩ

ΥΛζΛζ

Мг

t(Ka

— А Г —

22 — м >

' М

Ум

м<

(1 + е'

(Ка)

(59.58)

(59.59)

(59.60)

Последнее соотношение в (59.60) записано с учетом того, что

вектор 1, направленный от первого атома ко второму, противополо-

жен по знаку вектору, направленному от второго атома к первому.

Подставив (59.60) в (59.43), получим

ω-

2 [Мг ^ М

) — У \М

£2

А\

) 4 ^ M

А (Мг + МЛ

)

. =ωϊ

4М

где

ω;

2 \ М

) '

\±Y 1-^sin^],

4М{М

81Π'

Ка\

1; ω{γ

1 _j_

t(Ka) |2

(59:61)

2 А

'М

+М

Рассмотрим зависимость ω (/() в окрестности К = 0. Полагая

sin/(α/2 ^/(а/2, получим

ω* = ωφ± (l-Y

^)]. (59.62)

Для ветви ω(/(), соответствующей знаку минус в (59.62), имеем

(59.63)

384

фазовая ν

и групповая ν

Γρ

скорости равны и представляют

с0

бой скорость звука

ω άω щуа

-•

Г Аа

/сп

= V

Гк

= -f- = у

(Μι

Мг)

= с. (59.64)

Подставляя ω = 0 при

/С

= 0 в (59.46), получим

3-'· <

е. атомы колеблются синфазно и с одной и той же амплитудой.

Другими словами, ветвь, соответствующая знаку минус перед корнем

(59.61), описывает акустические колебания. Плюс в (59.61) описы-

вает оптические колебания:

ω(7() = ΐ/2ω

(ΐ-^). (59.66)

При К = 0 частота ω (0) = |/2ω

= j/~ А с ростом К час-

тота оптических колебаний ω уменьшается по квадратичному закону.

Фазовая скорость оптических колебаний стремится к бесконечности

при

/С

—^0, групповая скорость равна.нулю при К = 0. При аК12

=±

= π/2 находится минимальная частота оптических колебаний:

ω° (i) = ω

γΥ+ντΤψ

= ω?ηίη

(59.67)

и максимальная частота акустической ветви

аИ(£) = а>о}Л (59.68)

Как видно из общего выражения (59.61), ω° (/С)>со

(/С). Частота

акустических колебаний меняется от нуля до со£

ах

, частота опти-

ческих колебаний меняется в интервале от |/2 ω

до ω

]/"l + У\

—

Чем ближе к единице величина γ, тем больше спектральный интер-

вал оптических и акустических колебаний. Групповая скорость

точке К = ±п!а равна нулю. При γ=1 спектры оптических

акустических колебаний сливаются. При γ<

между ними имеется

некоторы й частотный интервал.

При многих расчетах можно считать, что оптические колебания

Сов

ерилаются примерно с одной и той же частотой которая

большинства кристаллов находится в инфракрасной области

Сп

ектр

излучения.

На рис. 83 приведен график зависимости ω (К) для оптических

акустических ветвей.

Найденные нами свойства оптических и акустических ветвей не

ависят от конкретного вида решетки, структура которой лишь

ияет на вид функциональной зависимости ω (К). Наибольшие

13 Киреев 385

максимальные частоты оптических колебаний соответствуют больщц^

длинам волн, поскольку фазовая скорость для оптической ветви

обращается в бесконечность при /С->0, в то время как групповая

скорость при этом обращается в нуль. Если максимальная

длина

волны оптических и акустических ветвей

не существует: Я

тах

= оо, то минимальная

длина волны существует:

KTR^

=2A> (59

)

что имеет вполне наглядный смысл. Очевид.

но, что минимальное расстояние' в про

странстве между точками, состояния коле

баний в которых имеют разность фаз 2π

для дискретно распределенных колеблю

щихся центров не может быть .меньше

чем 2а. Кроме того, дискретность К, вы-

текающая из периодических' граничных условий, имеет тот же

смысл

—

возможны лишь такие колебания, длины волн которых охва-

тывают целое число периодов решетки.

Частоты колебаний решетки лежат в интервале (0-2-10

) Гц.

Длинноволновые оптические колебания решетки (колебания с наиболь-

шими частотами) проявляются в спектрах поглощения^ и отражения

кристаллов в области длин волн в несколько десятков микрон.

Рис. 83. Оптические и аку-

стические ветви колебаний

решетки

Резюме § 59

1. Решая уравнение движения (59.8) в предположении, что част-

ное решение имеет вид гармонического колебания с частотой ω,

получим для амплитуд уравнение, совпадающее с уравнением матрицы

преобразования координат S. Из свойств матриц S и D следует,

что колебания соседних атомов происходят с постоянной разностью

фаз. Другими словами, гармонические колебания образуют бегущие

гармонические волны, идущие в направлении вектора К.

2. Вводя матрицу G, элементы которой представляют собой сумму

элементов динамической матрицы, умноженных на некоторый фазо-

вый множитель, сведем систему 3Ns уравнений к системе 3s урав-

нений, из решения которой получаются 3s различных ветвей зави-

симости ω (К). Три ветви казываются акустическими, остальные

(3s — 3)

—

оптическими.

3. Акустические ветви соответствуют синфазным колебаниям р

а3

личных атомов элементарной ячейки, когда все атомы совершают

колебания с одной и той же амплитудой и фазой. Для окрестности

центра зоны Бриллюэна связь между частотой и волновым число*

является линейной , *

аИ=с/С, (59.1Р>

где с —скорость звука.

386

4. Оптическим колебаниям соответствуют колебания атомов

противоположными фазами, амплитуды колебаний обратно пропор-

циональны массам атомов, поэтому центр массы ячейки остается

покое, в то время как смещения атомов приводят к разделению

зарядов, вследствие чего в ячейке возникает электрический диполь-

ный момент.

5. Различие между акустическими колебаниями отчетливо про-

является только в окрестности К =

О,

вдали от этой точки различие

между оптическими и акустическими колебаниями теряется.

§ 60. ТЕПЛОЕМКОСТЬ РЕШЕТКИ. СТАТИСТИКА ФОНОНОВ

В статистической физике доказывается, что вероятность нахож-

дения системы в состоянии с энергией E

равна

, (60.1)

где статистическая сумма Ζ определяется условием нормировки

=l, (60.2)

из которого для Ζ следует выражение

Z = 2

e kT

. (60.3)

Среднее, или равновесное, значение энергии

(E) = ^E

. (60.4)

Используем выражение (60.4) для нахождения равновесного зна-

чения энергии, гармонического осциллятора:

«("+т)

(£(*>= : / ι \.

оо (/Н-г j

2 ^ kf

η —0

_ пЛ(й,

2 пШ

ι 1=0

ηΐί(ύ„

* оо α

(60.4')

- /ι=0

13· 387

Знаменатель (60.4') вычисляется как сумма геометрической про-

грессии:

Г _2ΐ«Τ

= (60.5)

п = 0

1-е

Но так как

ОО ОО 00

1 ^ = (1^-= (Г^. (60.6)

п—О п=О п = О

ТО

оо ηΆ(ύ„

ΐίω,

— •——

е _

2 пИа

=hco

j- (Б0.7)

—

Ζ* * kT

nfito

п=\

Учитывая (60.4

—

60.7), запишем выражение для равновесного

значения энергии осциллятора:

ηω

1-е

-1

что находится в соответствии с функцией распределения Бозе —Эйн-

штейна! Из (60.8) следует

(60.9)

= + V.

\ e

-J

Обозначим отношение (Е

) к Ηω

через (п

W-JG- I + TS—·

;

60Л0

где (я

) есть «ιсреднее» значение колебательного квантового числа

осциллятора. '

При Т-> оо, когда йсо

<^7\ осциллятор находится в высоком

энергетическом состоянии:

«->=4+S~H;. ««Ο·

а его средняя энергия равна &7

) = (n

)h<o

= kT (60.12)

в соответствии с классической статистикой.

388

При малых температурах, когда

Λ(ύ

(60.13)

е. осциллятор находится в наинизшем колебательном состоянии:

Так как нулевая энергия осциллятора не принимает участия

в балансе энергии при взаимодействии осциллятора с окружающей

средой, то в дальнейшем ее опустим я будем считать, что средняя

энергия осциллятора равна

-ng^· (60.14)

-1

Воспользовавшись полученными результатами для гармонического

осциллятора, найдем среднюю энергию колебаний решетки. С этой

целью можем исходить из общего выражения (60.4), учитывая, что

= E(v

, υ

,...)=Σ

ηω

«{

* + Ύ) (

= 0

> ···) (

Если подставить (60.15) в (60.4), то получим общее выражение

для (Е), которое в силу независимости осцилляторов можно преоб-

разовать в сумму средних значений энергии каждого осциллятора

(60.10) или (60.14), так что

<β>-1<Εΐ-ζ-&-1Σ w-· <

Сумму (60.16) удобно разделить на две суммы —сумму по опти-

ческим

> 3) и сумму по акустическим (J -s; 3) ветвям колебаний:

Частоты оптических колебаний имеют узкий интервал значений,

поэтому ω

(Κ

)^ω? и

Пай ^ * МП®?

22^—2^-'·. <«·'

ак как Κα принимает N различных значений.

Введем некоторый характеристический параметр —температуру

Дебая 6]

—

соотношением

= (60.19)

389

Если положим ω?= 1,4· 10

-1

, то для температуры Дебая полу,

чим: 0]= 100° К. Для большинства веществ значения

Θ/

лежат в пре-

делах 100—400° К. Используя величины 0J, энергию оптических

колебаний можно представить в виде

= (60.20)

/=4 е

—1

Если 7>Θ?, то е

9/г

+ Ъ)!Т и

3 s

(Е°) = N 2

= (

)

NkT

> (60.21)

/==4

т. е. все оптические колебания возбуждены до высоких квантовых

состояний. Величину = можно рассматривать как число

fid) а

оптических фононов. При Т^б? в кристалле имеется большое число

оптических фононов, при оптические колебания практически

не возбуждены

—

(п^) ^ 0

— и

вклад в энергию колебаний решетки

они не дают.

В акустической ветви частота меняется от нуля до со^ квази-

непрерывно. В этом случае сумму по ω

;

(Κ

) можно заменить на

интеграл по частотам. Однако при этом необходимо знать плотность

состояний по частотам, поскольку в единичном интервале частот

(άω= 1) может содержаться различное число колебаний. Пусть число

колебаний в единичном интервале частот равно g(co), в таком случае

в интервале dco их будет

dN = g (ω) dco. (60.22)

Чтобы найти функцию g"(co), необходимо знать дисперсионное соот-

ношение ω (К). Если У —объем кристалла,'то в объеме УАтк^

η*Δτ

ν VAx

фазового пространства содержится —^— = элементарных

ячеек, при этом каждой ячейке соответствует одно возможное коле-

бательное состояние кристалла. Построим в К-пространстве шаро-

вой слой толщиной dK и радиусом К; объем слоя 4лК

dK, ему соот-

ветствует ~ ячеек, на единичный объем кристалла прихо-

4πΚ* dK

дится —g^g— ячеек.

Выразим эту величину через частоту: так как υ

Γρ

= άω/άΚ,

т0

άΚ = άω/ν

Γρ

. Выражая К через ω, так как 7( = /((со), получим

(

23)

Итак, плотность состояний колебаний решетки имеет вид

IW-FIG· «**>

390