Киреев П.С. Физика полупроводников

Подождите немного. Документ загружается.

является решением стационарного уравнения Шредингера. Решение

временного, уравнения Шредингера

= £(г, f) (55.2)

связано с решением стационарного уравнения простым соотноше-

нием

Е°

(а) .

Чй(г, 0 = ift(r)e

(55.3)

что легко проверяется непосредственной подстановкой (55.3) в (55.2),·

откуда вытекает (55Л).

Пусть при t = 0 на квантовую систему наложено некоторое поле

Λ '

= W(r, t). Гамильтониан системы имеет теперь вид

AAA

H =

H°

+ W. (55.4)

Волновая функция возмущенной системы ψ (г, i) определяется из

уравнения

ih ^ = Щ - (н° + w)

ψ.

(55.5)

Для решения этого уравнения согласно Дираку разложим (г, t)

функциям ψα (г, t),

(Г, 0= t)da. (55.6)

Мы записали разложение ψ (г, t) по ψ£(Γ, t)

считая, что а имеет

непрерывный спектр, в противном случае необходимо заменить ин-

теграл суммой по всем значениям а. Подставим (55.6) в (55.5):

<к„

(t)

д№ (Г,

01 ,

= \c

{f) {но^ (г, ί) + 4ίψ

(г, /)} da. (55.7)

Учитывая (55.2), получим

J »(г, ή da = ξ (0 Wi|4 (r, t) da. (55.8)

Умножим (55.8) слева на (г, t) и проинтегрируем по всему

пространству. Условие нормировки функций ψα(Γ)

• J

Ψβ* (

) Ψ»

(

) άτ = δ φ —а) (55.9)

позволяет записать

ч-^Э Ρ /А T^^-^^'iy; л /КС 1Λ4

,й

"ЗГ

· ί

Уравнение (55.10) —это уравнение (55.5) в матричной форме, оно

является точным уравнением. Решение его в общей форме крайне

351

затруднительно, поэтому оно решается обычными методами теори

возмущений; Пусть W мало, тогда его можно считать возмущением

За меру малости величин принимается малость матричного элемента

Ι^βα =

%* (г) w (г, 0

г|£

(г) dx = UV (0.

(55.

Ц)

Будем искать c

(t) в виде ряда

(t)=cb(t) + cW(t) + W(t) + ... (55.12)

' Л

Са (0 есть нулевое приближение, соответствующее W = 0. В нулевом

• л

приближении, когда W = 0, правая часть (55.10) обращается в нуль,

следовательно , в нулевом приближении da (ή являются констан-

А ,

тами —в полном соответствии с тем, что при W — 0 система нахо-

дится в стационарном состоянии. Рассмотрим состояние, которое

соответствует энергии £°(γ). Для него все с'а=0 при а Φ у. Так

как вероятность нахождения системы во всех состояниях а равна 1,

то при с

= 0 (а Фу) необходимо положить с

= оо, т. е.

4 = δ( α-γ). (55.13)

Чтобы получить уравнение для (ί), необходимо взять нулевое

приближение для с

(0> поскольку в уравнение (55.10) входит

}

(

) С

/ \ ТГ

<β>

£0 (a)]

' \V7

/Л A

= \ δ (a

—

γ) e

{t)d(x =

Уравнение (55.14) интегрируется элементарно:

(9 = тИ (t)^'dt, (55.15)

где

(β)—(7)

βν

Величина

(ί)

есть вероятность нахождения квантовой

cucmeMbi

в состоянии ψβ (г, t) в момент времени t. В момент времени t^

система находилась в состоянии я|4(г, 0). Используя выражение

(55.15), получим для вероятности |ср' (0

(01

=ж

\ (0 e

W dt

(55.16)

. ο

Эту величину можно рассматривать как вероятность перехода

системы из состояния (г, t) в состояние ψβ (г, t) под действие*

возмущения W в течение времени L

352

Вероятность перехода в единицу времени, которую обозначим как

ί£>(γ, β)>

можно

определить соотношением

Иг. β)=|ΐ4Γ(')Ι

= ~

jj dt

(55.17)

Рассмотрим возмущение, не зависящее от времени. Вынося мат-

ричный элемент возмущения из-под знака интеграла и интегрируя

по времени, получим

'.. <55.18,

Как показывает выражение (55.18), вероятность перехода из со-

стояния γ в состояние β имеет осциллирующий характер. Частота

осцилляций зависит от разности энергий. Если рассматривать w (γ, β)

как функцию ωβ

, то мы видим, что эта функция для каждого мо-

мента времени монотонно уменьшается с ростом частоты. Другими

словами, если рассматривать вероятность перехода как функцию

разности энергий между исходным и конечным состояниями, то ве-

роятность с ростом указанной разности падает.

sin ωβ

/ sin*

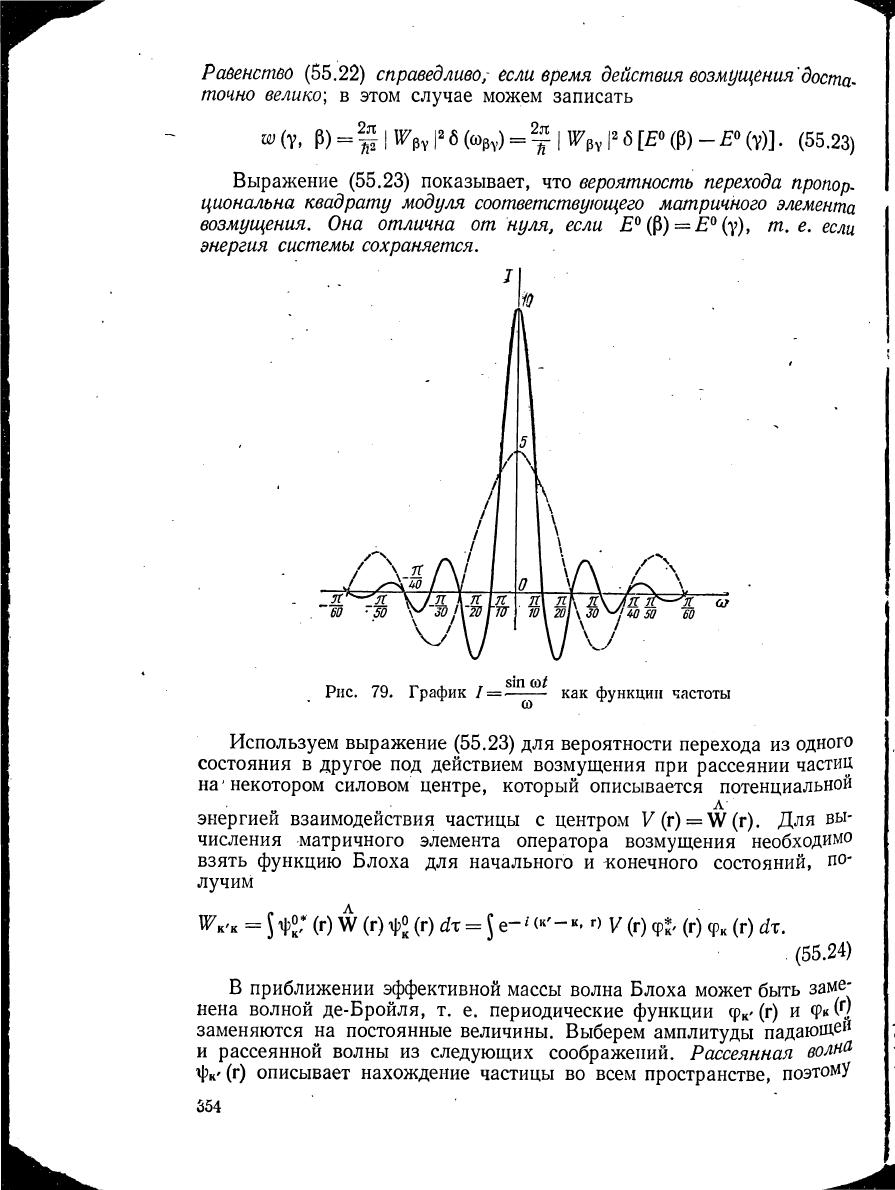
Рассмотрим величину /=

— = t как функцию частоты.

ω,3

ЕСЛИ ύ)β

-^0, то

lim/= lim f^L^t. (55.19)

βγ

-0 ω

βγ

-*0

βΥ

График функции I приведен на рис. 79.

Чем больше время тем больше величина максимума и меньше

интервал частот, охватываемый первым максимумом:

Δω

βγ

= ^. (55.20)

При. оо интервал частот основного максимума Δω

βγ

-»-0

и /оо.

Рассмотрим интеграл от I по частотам:

ОО 00

\ /Λο

βΎ

= \

sin

«W

d(Qp

= π. (55.21)

oo -i

βν

Таким образом, при больших интервалах t

1 sin a>R

12 Киреев 353

Равенство (55.22) справедливо; если время действия возмущения доста-

точно велико; в этом случае можем записать

ИТ, β) = §

^βγ

δ (*W = I

δ [Ε° (β) - Ε» (ν)]. (55.23)

Выражение (55.23) показывает, что вероятность перехода пропор-

циональна квадрату модуля соответствующего матричного элемента

возмущения. Она отлична от нуля, если Е° (β) = Е° (γ), т. е. если

энергия системы сохраняется.

Используем выражение (55.23) для вероятности перехода из одного

состояния в другое под действием возмущения при рассеянии частиц

на'некотором силовом центре, который описывается потенциальной

Л"

энергией взаимодействия частицы с центром l/(r) = W(r). Для вы-

числения матричного элемента оператора возмущения необходимо

взять функцию Блоха для начального и конечного состояний, по-

лучим

WVк =

\ ψ°

(г) W (г) ψο (г) dx =

е-' г) у

(г) ф

(г) φκ (r) dXt

(55.24)

В приближении эффективной массы волна Блоха может быть заме-

нена волной де-Бройля, т. е. периодические функции qv (г) и <рк(

]

заменяются на постоянные величины. Выберем амплитуды падают

ей

и рассеянной волны из следующих соображений. Рассеянная волна

' (г) описывает нахождение частицы во всем пространстве, поэтому

354

она должна быть нормирована на δ-функцию, вследствие чего запи-

шем ее в виде

- (г) = -V ё с«''>. (55.25)

(2п)

Падающую волну пронормируем, таким образом, чтобы она описы-

вала поток вероятности единичной величины. Так как плотность

потока вероятности определяется величиной

L = (55.26).

полагая ψ

(г) = Ае'

(кг)

, получим

iw = 2m* t

* (- fc)

- («) А] = йк =

V. (55.27)

Таким образом, единичной плотности потоку вероятности соот-

ветствует условие

|А|*

=1; A = -|/"I=]/g (55.28)

или

Ыг) = {"ш)

(55.29)

Подставляя ψ

(г) и ι|ν (г) из (55.29) и (55.25) в (55.24), получим

для матричного элемента оператора возмущения

= § -V

(к

'° (

) (ш)^ *

(КГ) άτ =

(2π)

з г е'

κΓ

V (г) dr, (55.30)

(2л)

(Пк)

где

χ =

к —

к'.

Обозначим через V

интеграл, входящий в матричный элемент (55.30),

= (г) άτ. (55.31)

Рассмотрим случай сферически симметричного возмущения:

)=V(/·). Для вычисления (55.31) удобно перейти к сферической

системе координат, направив полярную ось вдоль вектора κ:

оо π

2π

= 5 И

EIXR C0S К

(')

Ή DR SIN

Μ'

ООО

оо π

= 2π

^ r

(r) dr I ё™

cos s

' sin

L·'

№. (55.32)

о 0

* 355

Интеграл по θ' вычисляется элементарно:

π π

ыгcos

в>

n 0

/ db' = — J-

cos Θ

ixr

2 sin xr

Подставив (55.33) в (55.30), будем иметь

(55.33)

(55.34)

Запишем выражение (55.23) для вероятности перехода, используя

(55.34):

(

') = Т (2^1 Ух|»в[£(к)-Я(к')]. (55.35)

Если .проинтегрировать (55.35) по всем состояниям к', то получим

вероятность перехода w (к) из данного состояния к во все возможные

состояния для одной частицы, создающей поток единичной плотности,

следовательно, w (к) тождественно интегральному эффективному

сечению:

w (к) = S* = (к, к')

cLx

= JII

')] (

)

Интеграл по к' вычисляется элементарно, если учесть, что

άτ

= άΩ^γά(κ'*). (55.37)

Интегрирование по /с' сводится к замене /с' на /с:

С другой стороны,

(in)

s* = $σ(θ, ψ)άΩ.

Сравнивая (55.39) с (55.38), запишем

(55.38)

(55.39)

4 π

оо

2 от*

'Й2

(55.40)

Таким образом, найдя V

_, мы можем выразить дифференциальной

эффективное сечение через матричный элемент возмущения.

356

Резюме §55

1. Возмущение, наложенное на квантовую систему, находившуюся

некотором стационарном состоянии, вызывает переход из этого

состояния в другие стационарные состояния. Вероятность перехода

за единицу времени из состояния α в состояние β равна

φ)-Ε (α)

w^(t)e

Если возмущение не зависит от времени, то

w(a

=^|1Τ

βα

δ[£(β)~£(α)].

(55. lp)

(55.2ρ)

Матричный элемент вычисляется с помощью волновых функ-

ций стационарных состояний

ψβ (г)

и γ

(г).

2. Для сферически симметричного воз- /

мущения вероятность перехода (55.2р) по- /·

зволяет выразить дифференциальное эффек-

тивное сечение рассеяния:

σ(θ, φ) =

2/я* С τ

7 /

ч sin кг j

(55.Зр) Рис. 80. Связь между κ и

' " углом рассеяния θ

где V (г) характеризует энергию электрона в поле сферически сим-

метричного рассеивающего центра, а κ =

|κ

—к'

Так как согласно

(55.37)

/с

/с',

то .

x = 2/csiny,

где θ— угол рассеяния (рис. 80).

(55.4р)

§ 56. РАССЕЯНИЕ НА ИОНАХ ПРИМЕСИ

Применим общую теорию квантовых переходов, изложенную

предыдущем параграфе, для определения эффективного сечения

рассеяния электронов и дырок на ионах' примеси." Для этого необ-

ходимо записать энергию возмущения в виде

(56.1)

V(r) = ±

Плюс относится к случаю, когда заряды рассеиваемой частицы

иона одинаковые, минус означает, что носитель заряда и ион имеют

Различные знаки. Заряд иона обозначен через Ze, расстояние между

ионом и частицей равно г. Чтобы обобщить результаты, рассмотрим

Рассеяние частиц на центрах с экранирующим потенциалом:

(56.2)

357

Размер области действия поля центра рассеяния определяется

величиной /?= —. При

/е

= 0 —оо, что' соответствует кулонов-

скому полю заряда Ze. Потенциальная энергия (56.2) достаточно

хорошо описывает электрон (или дырку) в поле нейтрального атома,

при этом 10

СМ"

Чтобы найти дифференциальное эффективное сечение рассеяния,

необходимо знать Υ

4π

со

Ze*· „ . г sm кг

-K

r dr -a

ЕГ κ

2ί'εκ

^ [е-

КоГ

iKr

e~~

[yr

] dr

= ±

Ze 2

8 /Cg+X

(56.3)

Подставляя выражение (56.3) в (55.40), запишем выражение для

σ(θ, φ):

/Ω

4m*

Z4* ,ι

σ(θ, ф)

—— (56.4)

]/с§

+κ

Угловая зависимость σ(θ, φ) содержится в κ:

/п ч

„ /Ze

*(β , φ) = 4

σ(θ). (56.5)

[KJ

+ 4*

sin

Выражение (56.5) для рассеяния на ионах упрощается:

/с

= 0 и

Ьтах.

Ьта*

(

Ze2 1

"2"

(56.6)

Рис. 81. Максимальное

прицельное расстояние

при движении частицы

в иоле двух ионов

— известная- формула Резерфорда, полученная

им при описании рассеяния α-частиц полем

ядер.

Если вычислить 5* и а

из (56.6), то полу-

чим бесконечность. Это связано с тем, что малым

углам отклонения соответствует большое эффек-

тивное сечение, поскольку малым углам откло^-

нения соответствуют большие расстояния между ионом и рассеиваемой

частицей

—

большие прицельные расстояния При движении же

частицы в твердом теле нет необходимости рассматривать изменение

b от нуля до бесконечности. Можно установить верхний предел зна-

чения прицельного расстояния из следующих простых соображений.

Предположим, что два иона находятся на расстоянии R друг от

друга (рис. 81). Очевидно, что отклонение носителя заряда опреде-

ляется ближайшим ионом. Естественно выбрать в качестве верхнего

предела для прицельного расстояния величину R/2. Если концент-

рация ионов Nj, то среднее расстояние между ними N

, поэтому

358

1 .,-4-

верхний предел для Ь

тах

равен N j

. Ему. соответствует некото-

рый минимальный угол отклонения 0

, определяемый из условия

" Введение 0

позволяет получить конечное значение S*:

π π

о* О С /о\ ·

^Л π 1 /· Ze

\2 f sin

θ dd

Cm - · Cm

•π

θ θ

2 008

= π

/ Ze* \» / 1 _ Λ (56.8)

em*t>

j 1

sin3

| W^/

min

Найдем эффективное сечение проводимости а

f /лч/1 „м ·

fl/ifl

π / Ζβ2 \а ? (1 —cos θ) sin 0

σ,

2π \

(θ) (1 —

cos

θ)

θ d0

- ^ •· •

. V

л ein*—

(56.9)

min

Sin4

Учитывая, что

1 cos0 =2 sin

у; sin θ = 2 sincos γ, (56.10)

получим

π π

Γ*

min

(1 — cos 6) sin 8 de

1 ^L^ll-^-Slnsin^· (56.11)

sinl

T ' J

sin

(56.12)

Разим Gmin через bmax В соответствии с (56.7):

sin^

-у- 4W/

359

В таком, случае, учитывая (56.13), (56.8) и (56.9), получим для

S* и а

S* = π

-^Ϊ-яИ

(56.14)

Ze2 Да

= — 4π

(

Т^ЕГ,

]

ε/η*ι>

1п

4УУ/

ε/η*

Ζβ2

4 \

ет*г>

(56.15)

Выражение для S* имеет очень наглядный смысл: свободный носи-

тель заряда взаимодействует с ионом на любом расстоянии, поэтому

интегральное эффективное сечение рассеяния на ионе равно беско-

нечности. Но если учесть, что при большом числе ионов достаточно

ограничиться прицельным расстоянием Ь

, то для эффек-

тивного сечения получим величину, равную площади круга радиуса

&шах. Отметим, что чем больше концентрация ионов примеси, тем

сильнее они взаимно компенсируют поля, тем меньше интегральное

сечение рассеяния носителей заряда на них. Пусть N1= 10

см

-3

в этом случае Ь

тах

^10~

см и S* 10~

см

, что намного превос-

ходит величину S/, взятую нами в § 53 для оценки роли ионов

примеси в рассеянии. Если оценить длину свободного пробега, то

получим для Ν] = 10

см

-3

= 10~

см. Это означает, что ионы при-

меси играют значительно большую роль в рассеянии и определении

длины свободного пробега, чем предполагалось в § 53.

Зависимость // от концентрации ионов примеси сравнительно

слабая:

NiS*

1 4 8

"Τ=

(56.16)

nNj

В табл. 17 указано значение //, подсчитанное по формуле (56.16)

для некоторых значений Nj.

Та блица 17

Nj, см-з

1021

1018

1015

1р см

1,3· Ю"

1·,3· 10"б

1,3- ю-5

1,3. 10"

360