Киреев П.С. Физика полупроводников

Подождите немного. Документ загружается.

проводнике создается некоторое число свободных электронов и дырок.

Свободные носители зарядов создаются в результате ионизации ато-

мов примеси и атомов основного вещества; другими словами, в полу-

проводнике имеются свободные носители заряда и ионы. Как во всем

кристалле, так и в любом физически малом объеме вещества суммар-

ный заряд всех заряженных частиц должен быть равен нулю —это

и есть условие, электронейтральности, справедливое для незаряжен-

ного в целом тела.

Запишем условие электронейтральности для единичного объема

вещества. Для этого необходимо подсчитать заряд положительных

и отрицательных частиц.

Электроны возникают за счет ионизации донорной примеси и ато-

мов основного вещества. Переход электронов из валентной зоны

в зону проводимости или к атомам акцепторной примеси приводит

к созданию свободных дырок.

Отрицательный заряд создают свободные электроны и ионы акцеп-

торов, он равен

(η-\-

Νΐ)β~. Положительный заряд создают свободные

дырки, и ионы доноров общей величиной (р +

ДО

J)' е

Условие электронейтральности можно записать в виде

(p + Ni)e+ + (n + Nz)e~ = 0. (30.1)

Учитывая, что

е~ —

—е

, получим уравнение электронейтральности

(n + N*)-(p +

N+)

= 0. (30.2)

Если обозначить через /г

, р

, п

&у

число электронов и дырок,

находящихся на донорном и акцепторном уровнях, то можно запи-

сать ряд очевидных соотношений:

ДО

-ДО£

= ДО

-р

;

Ν$

= Ν

-η

= ρ„

В таком случае уравнение электронейтральности (30.1) или (30.2)

можно записать в одной из таких форм:

(я + я

)-(р + р

) = 0, (30.4)

или

η +

/г

—

Л/д —

(30.5)

• · - <

Чтобы составить уравнение, из которого можно определить поло-

жение уровня Ферми, необходимо выразить входящие в уравнение

электронейтральности (30.5) величины через F. Выражения для η

Ρ известны, необходимо найти я

и р

(или п

и р

). Чтобы найти

число электронов, находящихся на примесном уровне, необходимо

знать функцию распределения электронов по примесным состоя-

ниям.

Легко видеть, что функция Ферми —Дирака не может быть

использована непосредственно для описания распределения электро-

181

нов по примесным состояниям, так как она справедлива в том слу.

чае, когда в данном энергетическом состоянии может быть два

элек-

трона с противоположно направленными спинами. Однако в состоя-

нии с энергиями £

или Е

может быть не более одного электрона.

Если поместить в состояние с Е

или Е

еще один электрон, то

в силу большого электростатического взаимодействия между

элек-

тронами энергия £

или Е

резко меняется. Другими словами уровни

энергии однократно и двукратно ионизированной примеси отличны

друг от друга. Невозможность .нахождения двух и более электронов

в примесном центре с энергией £

или Е

должна отражать функ-

ция распределения электронов по состояниям. Расчет по методу

Гиббса для систем с переменным числом частиц приводит к выводу,

что для примесных состояний функция распределения электронов

должна иметь вид

e!-F .. (30.6)

i-e π +1

8ι

где ^

—

степень вырождения ί-го примесного состояния. Если E

= Е

принадлежит донорной примеси, то gi = 2. Если Е

(

= Е

при-

надлежи т акцепторной примеси, то 1/2; таким образом распре-

деление электронов по донорным уровням определяется выражением

/= ЕЬ • (30.7)

1 ——

уе +1

а распределение электронов по акцепторным уровням имеет вид

/=—τρρ—(30.8)

2е *

Для дырок функция распределения имеет соответственно вид

fp~ ί fp — Ρ—Ε · (30.9)

£ ι

4-1

+1 i-e

Теперь легко найти число электронов или дырок, находящихся

на примесных уровнях. Найдем, например, я

(

)№ =ΝЛ * (Е-£

) —ст dE .

(30.10)

182

Аналогично можно наити п

, р

Ν„

2е

Ν,

Ρ д

f—я,

(30.11)

(30.12)

Запишем уравнение электронейтральности (30.5) с учетом явных

выражений (29.1), (29.13), (30.10) и (30.12) для п, р, п

и р

4л

{E — E^dE

£ —f

N„

(30.13)

+1 ^ +1

Если рассматривать это уравнение относительно уррвня Ферми,

то оно может быть сведено к алгебраическому уравнению четвертой

степени. Решать в общем виде его очень сложно, поэтому рассмот-

рим ряд частных случаев, имеющих важное практическое значение.

Кроме того, необходимо помнить, что уравнение записано для слу-

чая, когда имеется всего лишь один донорный и один акцепторный

уровень. В противном случае уравнение (30.13) будет еще более

сложным.

§ 31. СОБСТВЕННЫЙ ПОЛУПРОВОДНИК

Полупроводник, в котором примесь Ν

= Ν

= 0 отсутствует,

называется чистым или собственным полупроводникомУравнение

электронейтральности имеет вид

п-р = 0, или

/г

= р, (31.1) - 9 ft—S-

т. е. переход каждого электрона из валентной ДЕ

зоны порождает в ней дырку, поэтому число

дырок в собственном полупроводнике всегда

равно числу электронов (рис. 49). При усло-

вии (31.1) уравнение (30.13) для определения

положения уровня Ферми имеет вид

~7= Φΐ/2 (?)

~7= Φΐ/2 (ή)·

V я у η

(31.2)

Рис. 49. Генерация элек-

тронов и дырок проводи-

мости в собственном полу-

проводнике

Предположим, что N

= N

для этого необходимо, чтобы эффек-

тивные массы для плотности состояний были равны, т. е. т% = тр

β этом случае

Φι/

(Ι) = Φι/2(η), (31.3)

183

следовательно, ξ = η или, учитывая выражения (29.3) и (29.12),

получим -

F — Ec __

— F /οι .

kT - kT ' .

откуда

F = = (31.5)

т. е. уровень Ферми от температуры не зависит и лежит точно

посредине запрещенной зоны (совпадает с Е

Поскольку ширина запрещенной зоны для полупроводников

много больше, чем 2kT, то —

и — 1; собственный полупро-

водни к является невырожденным и интеграл Ферми равен -^е^

Vn £ '

и соответственно, поэтому для концентрации электронов и ды-

рок получим следующие выражения: ·

E-F АЕ

б £

n = N

et = N

e '

2kT

, , (31.6)

p = N

e^=N

2kT

. (31.7)

Энергия активации 6E

для собственного полупроводника равна

половине ширины запрещенной зоны.

Мы получили выражения (31.6) и (31.7) в предположении, что

= N

. Пусть N

. Но поскольку они являются величинами

одного порядка, интеграл Ферми опять-таки можно представить

в виде е^ и сокращая (31.2) на получим

n = N

e* = N

& = p

(31.8)

или

= (31.9)

Из (31.9) следует

F =

= (31.10)

Так как

/тМЗ/2 у

«лз/2

ν \ΚαΙ

ТО

«si.ii»

Через т*а дана величина, которую раньше обозначали как ш·

Уровень Ферми при Т=0 лежит в середине запрещенной зоны; он

184

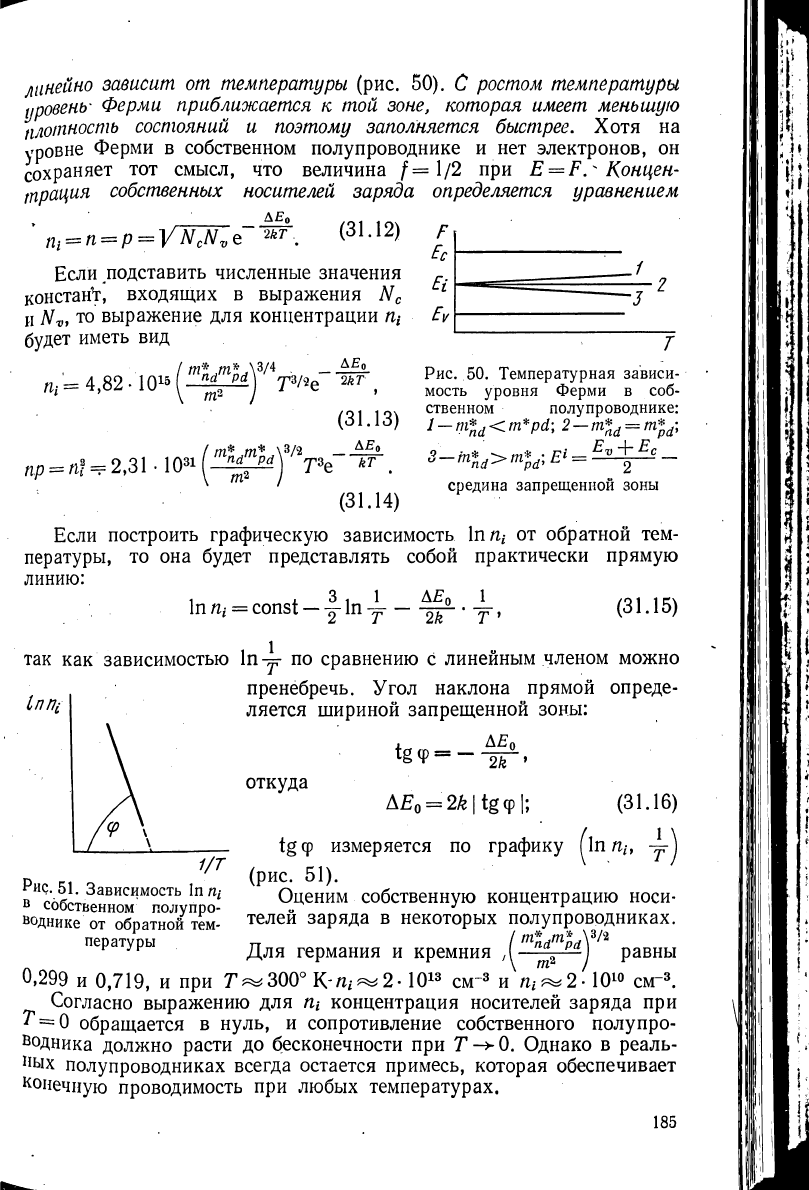
линейно зависит от температуры (рис. 50). С ростом температуры

уровень· Ферми приближается к той зоне, которая имеет меньшую

плотность состояний и поэтому заполняется быстрее. Хотя на

уровне Ферми в собственном полупроводнике и нет электронов, он

сохраняет тот смысл, что величина /=1/2 при Ε = Fг Концен-

трация собственных носителей заряда определяется уравнением

* = р = (

31Л2

Если подставить численные значения

констан'т, входящих в выражения N

и Ν

, то выражение для концентрации по-

будет иметь вид

Ее

Εν

= 4,82

3/4

3/2

ΔΕ ρ

2k Τ

(31.13)

Рис. 50. Температурная зависи-

мост ь уровня Ферми в соб-

ственном полупроводнике:

1 —

<m*pd\ 2 —т.]

η.ρ

= η?==2,31 · 10

-Mi

ad"

m2 j

ТЧ

Ά — M*

•

" nd·^ pd' — 2

(31.14)

средина запрещенной зоны

Если построить графическую зависимость In

от обратной тем-

пературы, то она будет представлять собой практически прямую

линию:

(31.15)

1 , 3.1 Δ£

= const

—

1η

так как зависимостью

1η

γ по сравнению с линейным членом можно

пренебречь. Угол наклона прямой опреде-

ляется шириной запрещенной зоны:

Inn;

Δ£ο

откуда

tgv ——

Δ£

= tg φ

(31.16)

1/Τ

Рис. 51. Зависимость In щ

собственном полупро-

воднике от обратной тем-

пературы

tgcp измеряется по графику [\пщ, γ

(рис. 51).

Оценим собственную концентрацию носи

телей заряда в некоторых полупроводниках

равны

Для германия и кремния

0,299 и 0,719, и при 7^300° 10

см~

и m"L 2

см"

Согласно выражению для щ концентрация носителей заряда при

^ = 0 обращается в нуль, и сопротивление собственного полупро-

водника должно расти до бесконечности при Τ0. Однако в реаль-

ных полупроводниках всегда остается примесь, которая обеспечивает

конечную проводимость при любых температурах.

185

В заключение этого параграфа рассмотрим вопрос о концентра-

ции носителей заряда в полупроводниках, имеющих вырожденные

зоны, подобно р-германию и р-кремнию.

Каждая зона характеризуется своей эффективной массой т

Р1

/Пр

. ПЛОТНОСТЬ СОСТОЯНИЙ ДЛЯ НИХ может быть записана в виде:

/ 2/72*

\ 3/2

(E) = 2n[-

]

j (Е

-Е)**

. (31.17)

(E) = 2N(^Y\E

-E)V*. . " (31.18)

Введем полную плотность состояний

/2т* \ з/2 ' .

N(E) = N

(E) + N

(E) = 2n[-

^J (Ε

-Ε)**

(31.19)

где

(m*

)V* = (mj

rfl

)

8/a

+ «л)

*, (31.20)

после чего можно воспользоваться выражением (31.13) для концент-

рации носителей заряда. Если вырождение имеет кратность g·, то

необходимо сложить эффективные массы плотности состояний с уче-

том числа максимумов М- для каждого сорта дырок (конечно, ана-

логично и для электронов) в степени 3/2.

, Легко видеть, что отношение концентраций дырок разного вида

определяется только плотностями состояний для них:

i <,,*„

v2 \

pd2/

т. е. легких носителей заряда должно быть меньше, чем тяжелых.

Для германия и кремния отношение масс

п?

1т%

легких и тяжелых

дырок равно 0,13 и 0,3, поэтому концентрация легких дырок должна

составлять примерно 0,047 и 0,165 от концентрации тяжелых дырок.

Концентрация легких дырок в германии составляет 4,5% и в крем-

нии 14% от общего числа дырок.

В заключение этого параграфа рассмотрим случай, когда ширина

зоны невелика: &E

<^kT. Если зона проводимости перекрывается

с валентной зоной на величину Δ, то вещество называется полуме-

таллом. В данном случае рассмотрен чистый, или собственный,

полуметалл с отрицательной запрещенной зоной

-E

= - Δ. (31.22)

При kT Δ полуметалл может быть вырожденным одновременно

как по электронам, так по дыркам, поэтому для концентрации

электронов и дырок можцо использовать выражения (29.14р) и

(29,15р) и записать:

(31.23)

/г

2m* W«

"Pd

δρ

, (31.24)

186

где

= F-E

\ F; б

+ 6

= Е„-Я

= Л. (31.25)

При повышении температуры вырождение одного из газов может

быть снято. Наиболее вероятно снятие вырождения для дырочного

газа, поскольку эффективная масса дырок больше эффективной

массы электронов, и быстрее заполняется зона проводимости. Когда

уровень Ферми перейдет из области перекрытия выше потолка ва-

лентной зоны,' сохранится вырождение только электронного газа.

В области двойного вырождения из (31.23—24) с учетом п = р

имеем

"mSA-тгЛ (31.26)

* 4_т* '

т* 4-т*

пл г

пи

пн

Г)

= , l

. Δ; δρ— , Д. (31.27)

т*

4- т* ' Р т* 4- т* ν · /

"nd^'^Pd "'nd^'^pd

"Для собственной концентрации полуметалла в области вырож-

дения электронного и дырочного газа имеем

8π

2 m* /я*. Wa

n = p = = Δ

. (31.28)

Как видим из (31.28), собственная концентрация полуметалла

в вырожденном состоянии определяется перекрытием зон энергии

Δ при Δ = 0 и

Л/

= 0.

Для полупроводника с положительной запрещенной зоной одно-

временное вырождение электронов и дырок невозможно. Но если

эффективная масса электронов значительно меньше эффективной

массы дырок, то уровень Ферми может оказаться в зоне проводи-

мости, в результате чего в собственном узкозонном полупроводнике

электронный газ окажется вырожденным. Такое состояние реали-

зуется, например, в теллуриде ртути, для которого термическая

ширина запрещенной зоны (но не параметр Кейна E

) равна нулю.

§ 32. ПРИМЕСНЫЙ ПОЛУПРОВОДНИК.

ПРИМЕСЬ ОДНОГО ВИДА

Рассмотрим полупроводник, в который введена примесь одного

вида, например донорная, так, что Ν

Φ 0 и N

= 0. Уравнение нейт-

ральности (30.5) примет вид

п + η

-ρ = Ν

, (32.1)

Или

n=p + Nt (32.2)

Уравнение (32.2) имеет очень наглядный смысл. Свободные элект*

Роны возникают благодаря переходам из валентной зоны, что при·

водит к созданию ρ свободных дырок, и с уровня примеси, благодаря

чему возникает Ν^-ионов донорной примеси (рис. 52). Уравнение

(32.2) относительно F является уравнением третьей степени. Однако

можно найти ряд сравнительно простых случаев, для которых можно

легко определить положение уровня Ферми и тем самым концентра-

цию электронов и дырок.

Прежде всего отметим, что в невырожденном полупроводнике

достаточно определить концентрацию носителей заряда только одного

знака, концентрация носителей заряда другого знака легко вычис-

ляется на основании соотношений (30.5) и (31.12):

АЯо

пр = п} = N

(32.3)

Выражение (32.3) показывает, что произведение концентраций элект-

ронов и дырок в невырожденном полупроводнике не зависит от поло-

жения уровня Ферми и тем самым от

наличия в полупроводнике примеси и равно

квадрату концентрации в собственном по-

лупроводнике. Соотношение (32.3) позво-

ляет находить концентрацию одного из

компонентов по другому. Например, если

концентрация электронов известна, то кон-

центрация дырок находится на основании

соотношения

ДЕо

NNjb

Рис. 52. Тепловая генерация

носителей

заряда в полупро-

воднике с донорной при-

месью

Р-4

(32.4)

Вернемся к уравнению (32.2). Так как свободные электроны

возникают благодаря ионизации примеси и основного вещества, то

при данной температуре эти два процесса могут играть неодинако-

вую роль. Для перевода электрона из валентной зоны в зону про-

водимости необходима энергия, равная ширине запрещенной зоны

АЕ

0у

в то время как для перевода электрона с уровня примеси

в зону проводимости необходима энергия, равная энергии ионизации

примеси которая много меньше ширины запрещенной зоны.

Поэтому при низкой температуре основную роль будут играть пере-

ходы электронов с примесного уровня, следовательно, ρ N д. Нера-

венство сохранится до тех пор, пока вся примесь не будет ионизо-

вана. Однако с.ростом температуры произойдет ионизация примеси,

и рост концентрации электронов η будет происходить вместе с ростом

концентрации дырок ρ. При больших температурах

и полупроводник станет собственным. Понятие больших и малых темпе-

ратур должно быть связано с концентрацией примеси. Одна и tna

же температура может быть или большой, или малой в зави-

симости от концентрации примеси — при малой концентрации

она может оказаться большой, при большой концентрации

малой.

187

1. Низкие температуры. Рассмотрим малые температуры,

при которых основную роль играет ионизация примеси, в этом слу-

чае

уравнение (32.2) упрощается:

/г

= Л^, или п = р

. (32.5)

Подставляя в (32.5) выражения для η и р

, получим

n = N

e ы

= =

д . (32.6)

д_

2е

Обозначив e

= χ, получим

x[l +2e *Τχ) = Ν

, (32.7)

или

e ^

л:

+ УУ

е *

χ-Ν

= 0, (32.8)

- ' . 1 ii л,

+ ^ =0. (32.9)

Решая уравнение (32.9) относительно χ, получим

ι --

/ / \

* = '( + ]/ 1 L (32.10)

Так как *>0, минус перед радикалом необходимо отбросить,

и из (32.10)

(32.11)

Напомним, что выражение (32.11) соответствует столь низким

температурам, при которых и n = N^

т. е. электроны про-

водимости возникают в основном за счет ионизации донорной примеси.

Рассмотрим два предельных случая для F. С ростом температуры

ifa.

е kT

. стремится к единице, N

возрастает и может стать больше Ν

Λ9

однако при достаточно малых температурах может быть выполнено

Не

равенство

J од/ д.

*£f-e

>1. (32.12)

поэтому для X получим

1 £л г-пТГ

с-

КГ

с +

ц F

ekT

V lt

=]/ (

)

189

Из (32.13) запишем выражение для положения уровня Ферми:

При 7 = 0

(32Л4)

+ F а

^ = (32.15)

т. е. уровень Ферми лежит посредине между дном зоны проводимости

и примесным уровнем. При повышении температуры уровень Ферми

повышается, проходит при некоторой температуре через максимум,

затем опускается. При 2N

= N

он снова находится в середине

между Ε с и £

. Однако для этой области температур справедливость

формулы (32.14) определяется величиной концентрации Ν

: для

малых концентраций примеси N

равно Ы

/2 при таких температу-

ДЕд ЛЕд

рах, для которых е

2/гГ

^>1. Если же Ν

велико, так что e

2kT

то формула (32.14) для F не применима.

Найдем величину концентрации электронов:

n = N

В-'?

= (32.16)

Обращает на себя внимание, что при малых температурах кон-

центрация электронов определяется концентрацией примеси в сте-

пени 1/2. ~

Если построим график (1η η, 1 /Т), то увидим, что он имеет

практически вид прямой линии с тангесом угла наклона, равным

AEJ2k, в то время как для собственной концентрации угол наклона

определяется величиной AEJ2k.

Теперь рассмотрим противоположный случай:

^е <1; или (32.17)

Для этого необходима при той же концентрации доноров доста-

точно высокая температура с тем, чтобы 8N

. Разлагая радикал

(32.12) в ряд и ограничиваясь первым членом, получим

Ч 4 Ν

Л£д

\ N

=т

sr+

---"

)

eB,

· <

18)

Из (32.18) для уровня Ферми следует выражение

F = E

+ kT (32.19)

100