Киреев П.С. Физика полупроводников

Подождите немного. Документ загружается.

Поскольку функций распределения зависит от энергий,

n = 2\f

(

E, T)dE \ (28.48)

(Я) (S

)

Сравнивая (28.48) с (28.12), имеем для плотности состояний

] та"· (

)

1 1

Для .сферических изоэнергетических поверхностей получаем из

(28.49) -

Для квадратичного закона дисперсия (28.50) приводит к (28.23)

и всем последующим соотношениям. Однако для неквадратичного

закона дисперсии соотношение (28.49) является более подходящим.

Найдем на его основе выражение для плотности состояний с исполь-

зрванием' дисперсионного закона Кейна (26.37). Если для зоны про-

водимости за начало отсчета энергии принять дно зоны проводимо-

сти; то (26.37) примет вид после вычитания E

£(к)=—f +ГЩ-+У — + (28.51)

Поскольку Р~6· Ю

-8

эВ -см, при малых к можно отбросить

второй член и записать

Г Е

Ί2 2PW Е*

[£(K) + -fJ = — + , (28.52)

или

= + (28.53)

Из (28.51) в общем случае для

£| найдем

= Щ- = +

А9

(4Р2/3)к

_, (28.54)

dK т

]/1 PW+EgV*

ли в пренебрежении членом %

к!т: <

£·

= ^

1 1

(2Р2

2/3

Подставив (28.55) в (28.50), получим

Vk£|

(2P^/3+fii/4)'/

' . -

{2Ь

ЬЬ)

Зк

у -|р2

К2+

А.·

N(E)= ' « (28.56)

171

Исключая к в соответствии с (28.53), для (28.56) получим

N (£") =

•

1/2

{Е +Е)

1Р

4л

2Р

\з/2

(28.57)

Введем эффективную массу на дне зоны проводимости mj* соот-

ношением

(28.58)

4Р2

ЭТО позволяет записать (28.57) по аналогии с ранее использо-

ванными выражениями:

1 /2т°* \з/2 / ЕЛ

1/2 /

. £ \

£1/2

(

+я7)

О+г^)·

(28

59)

При E

= 0 выражение для Ν(£) проще получить из (28.57):

4πΡ

^3/2

(28.60)

При Р~6- 10"

эВ-см имеем Ν (Е) [см*

] ~ 5,4-10

[£(эВ)]

§ 29. КОНЦЕНТРАЦИЯ ЭЛЕКТРОНОВ И ДЫРОК

Запишем теперь выражение (28.13) для концентрации электро-

нов, в которое вместо Ν (Е) подставим выражение (28.35). Это можно

сделать потому, что функция Фер-

ми—Дирака очень быстро умень-

шается с ростом энергии, поэтому

вклад в концентрацию электро-

нов от верхних энергетических

состояний будет крайне мал, и ис-

пользование (28.35) для Ν (Е) при

всех значениях не приводит к за-

метной ошибке в п. В качестве

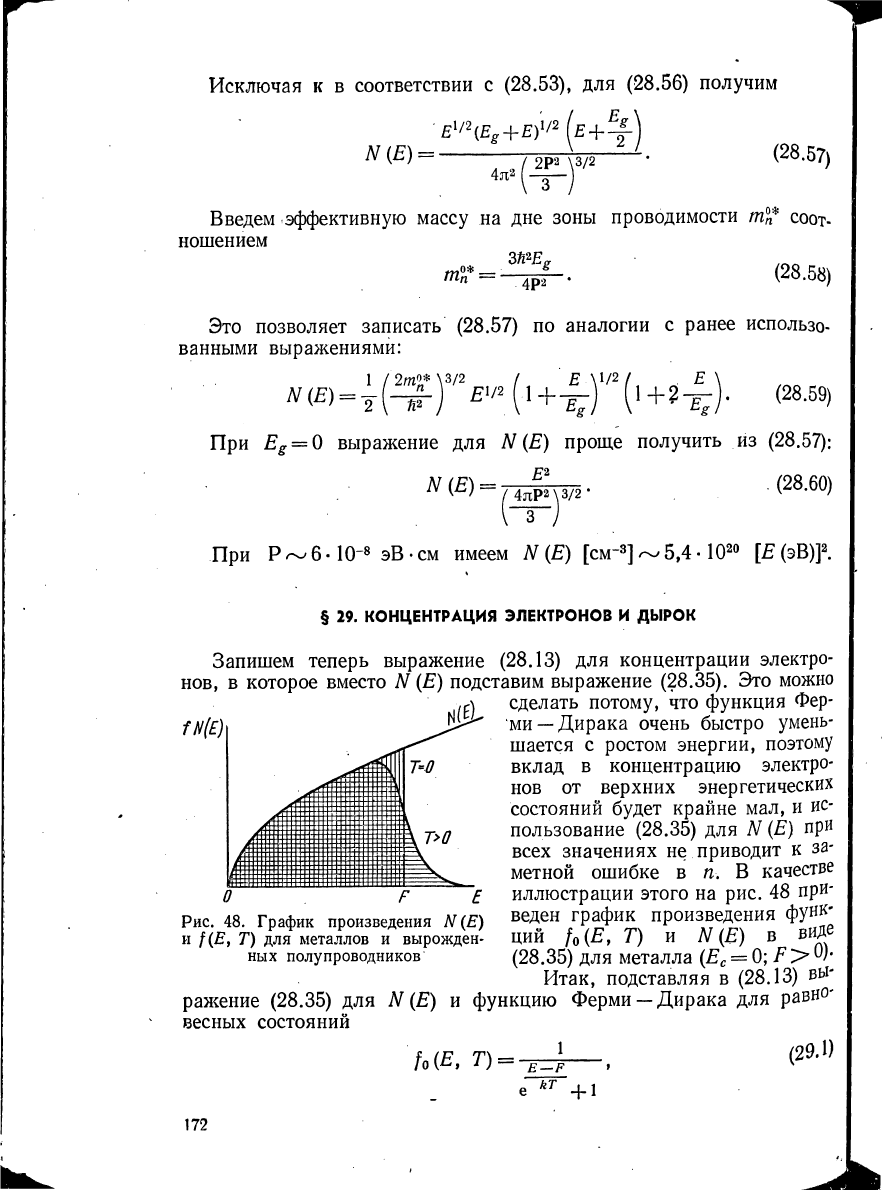
иллюстрации этого на рис. 48 при-

веден график произведения функ*

ций f

(E, Τ) и Ν (Ε) в виде

(28.35) для металла (Е

= О;F>

)·

Итак, подставляя в (28.13) в

ь1

ражение (28.35) для Ν (Е) и функцию Ферми —Дирака для равн

F Ε

Рис. 48. График произведения Ν (Е)

и /(£, Т) для металлов и вырожден-

ных полупроводников

весных состоянии

(£, Т)=

(29.1)

172

получим

оо

= 2

/о

(Ε, Τ) Ν (Ε) dE = 2

'. (29.2)

J J . kT , ι

e +1

Если величина F известна, то выражение (29.2) позволяет вычис-

лять концентрацию электронов.

Перепишем выражение (29.2) для п, перейдя к безразмерным

переменным. Для этого положим

C άχ =

~ΊΤι ^ kT° " <

)

в таком случае

Введем следующие обозначения:

/2nm*kT\3/2

[-ll·-) =

<> (29.5)

о ~

Величина N

носит название эффективного числа состояний в зоне

проводимости у α Φι/2 (ξ) называется интегралом Ферми порядка 1/2.

В новых обозначениях концентрация электронов η имеет вид

П==

Т^

®·

(29

Концентрация электронов является функцией температуры

и уровня Ферми п = п(Т, F). Интеграл Ферми Φι/2 (ξ) в общем

виде в элементарных функциях не выражается, но для целого ряда

важных в практическом отношении случаев существуют приближен-

ные аналитические выражения, которые получим дальше.

Перейдем к нахождению выражения для концентрации свободных

Дырок в валентной зоне. Плотность состояний у потолка валентной

зоны определяется соотношением (28.39). Функция распределения

Дырок по состояниям имеет вид

(Ε, Τ) =

/о

(Ε, Τ) -

, (29.8)

В таком случае число дырок dp в интервале энергии dE равно

числу состояний 2N (Е) dE, умноженных на вероятность того, что

они заняты дырками

—

dp = 2N (E)f

(E, Τ). (29.9)

173

Концентрация дырок в валентной зоне равна

р = 2 J f

(E, Τ) Ν (Ε) dE.

(29.10)

Нижний предел, равный E

v mIn

, заменили на —оо, учитывая

резкую зависимость /

от энергии. Подставляя выражение (29.8)

для }

0р

и (28.39) для Ν (Ε), получим

Р —2 ^ 2ρ

— Ε

-со

(29.11)

В выражениях (29.9— 11) и дальнейших отсчет энергии для дырок

совпадает с направлением отсчета энергии для электронов.

Введем обозначения:

Еу-Е _ E

-F

Л, ил

— ,

"~ kT

используя их, перепишем (29.11)

= η>

2m* /г7Л 3/2

ρ = 4π —

V'* С χ

ι/2

dx 2Ν

где

Ν.

· = 2(·

2nm*

kT \з/2

Λ2

есть эффективное число состояний в валентной зоне, а

4*dx

1/2

<Ч>-$

е^-Ч+1

(29.12)

(29.13)

(29.14)

(29.15)

есть интеграл Ферми, совпадающий по форме с Φι

(ξ).

Согласно (29.7) и (29.13) концентрации электронов η и дырок ρ

зависят от температуры Τ и уровня Ферми F.

Для интеграла Ферми Ф

1/2

существуют различные приближенные

выражения, справедливые в той или иной области изменения аргу-

мента, а именно:

Φι/2&) =

при —οο<ξ<- 1,

^•o^W πρΗ-1<ξ<5, (29·'

у ξ

при 5 < ξ < оо.

174

Первое приближение, справедливое при ξ<—1, соответствует ста-

тистике Больцмана. Условием применимости классической стати-

стики является неравенство ξ< —1 или

<.—1

откуда F<

— m. е. полупроводник является невырожденным (подчи-

няется классической статистике), если уровень Ферми лежит ниже

зоны проводимости не менее чем на kT. Если уровень Ферми лежит

выше Е

более чем на 5kT, то полупроводник полностью вырожден-

ый. Если Е

—

kT<F<E

+ 5kT, то свойства полупроводника

являются переходными от невырожденного к полностью вырожден-

ному. Как видим,

в условие вырождения входит температура и поло-

жение уровня Ферми относительно дна зоны проводимости. Далее

свяжем эти условия с другими характеристиками вещества и прежде

всего с концентрацией· примеси.

Покажем, что приближенные выражения для Ф1/2 (ξ), записанные

выше, действительно имеют место.

Из выражения для Ф1/2® непосредственно видно, что при ξ<—1

экспонента при любых лг>0 будет больше единицы; Но

это значит, что при любых ξ<—1 функцию Ферми—Дирака можно

заменить функцией Больцмана:

e«-6 + i (при ξ<-1; *>0). · (29.17)

В таком случае

оо оо

' Φι/2

(Ό ^ = \x

e~*dx.

(29.18)

о о

Последний интеграл в (29.18) есть гамма-функция Эйлера Г (3/2)

(он может быть сведен также к интегралу Пуассона):

СО

Г (3/2)= J xi/*e-*dx = (29.19)

- (29.20)

полном соответствии с (29.16).

Запишем выражение для концентрации электронов в невырожденном

Щпроводнике:

2N „ t ,

/2nm*kT\V2 -

* = Φι/2(ξ)~·Ν,et = N

e ^ = f-j e ^ ;

F<E

-kT. (29.21)

175

Эффективное число состояний N

зависит от температуры. Под.

ставив численные значения универсальных констант, входящих в N

получим

I 2nm*kT

\з/2 / mS \

//и5\з/2

Τ \з/2

1015

bf)

гз/2

1019

и)

у .

(29.22)

£ —F

/mS\3/2 £

η = 4,82·10

Μ-) ТУ

е *

. (29.23)

Рассмотрим теперь случай полностью вырожденного полупровод-

ника, для него:

. Φι/2© = 4ΐ

3/2

= 4(-^^)

3/2

(F>F

+ 5kT). (29.24)

Концентрация электронов при этом будет' равна

2N 8л

2т*

\з/2

ф|/!

Τ \ΊΠ <

·^· <

т. е. она не зависит от температуры. Напомним, что уровень Ферми

находится в зоне проводимости выше ее дна не менее чем на 5kT.

Найдем те условия, при которых интеграл Ферми может быть

представлен в виде Ф1/2 (ξ) =

-3-

3/2

. Как известно, при малых темпе-

ратурах ggj^S (Ε

—

F). Это приближенное равенство позволяет

легко вычислить интегралы от произведения двух функций

(E)f

(E, Τ).

Действительно,

оо оо оо

$ φ(β)/ο(£, T)dE = x(E)f

(E, Τ) I- =

= —Χ(0)/ο(0, T) + %(F)^

(F)-%(0), (29.26)

•

где

(E) = l<p(E)dE, a f

(0,T)^\. (29.27)

Пользуясь этим свойством функции распределения Ферми

—

Дирака,

можем легко получить выражение для концентрации. В данном

случае

<p(E) = (E-E

)W и χ (£) = | (£-£«)»/*,

поэтому

1/2

Κπ (*Г)

3/2

с е +1

c Л(Р-Е VV2 (29.28)

Κπ (kTf/

с)

· ^

176

Из выражения (29.28) действительно видно, что

Φι/2 (I) = 4 (и^)

3/2

= 4 ξ

3/2

. (29.29)

Условие независимости η от температуры равносильно условию,

чт0

"""" (E

—

F)· Но для этого необходимо, чтобы f

Τ)

менялась в области E^F как можно быстрее, при этом чем уже.

область (E

—

F) изменения f

(E, Τ), тем ближе ее производная к δ-

функции, δ-образный характер —f

(Ε, Τ) лучше проявляется при

низких температурах.

В переходной области от невырожденного к полностью вырож-

денному случаю концентрация электронов η будет зависеть от тем-

пературы:

n = N

(29.30)

0,25+

Результаты, полученные для электронов, могут быть легко пере-

несены на дырки. С этой целью достаточно записать выражение для

Φι/2 (η) в виде (29.16):

V π „ ^ ^ ι

2~e

при — οο<η<— 1,

Φι/2 (η) = {

ρΗ -1<η<5, (29.31)

—

η3/2

5<η<οο.

В невырожденном полупроводнике концентрация дырок опреде-

ляется статистикой Больцмана, условием применимости которой

является неравенство

—

< —1 или F>E

+ kT, ' (29.32)

w. е. в невырожденном полупроводнике уровень Ферми должен лежать

выше потолка валентной зоны по крайней мере на величину kT.

Для полностью вырожденного полупроводника

η =

\/ > 5 или F<E

-5kT, (29.33)

- е. уровень Ферми в полностью вырожденном полупроводнике дол-

жен находиться в валентной зоне

ниже ее потолка на величину не

менее 5kT.

Если учесть замечания об изменении направления отсчета энер-

гии для дырок на противоположное, то все результаты для дырок

Должны быть подобны результатам для электронов при соответствую-

щей замене характеристик электронов характеристиками дырки.

177

Запишем выражения для концентрации дырок для двух предел^

ных случаев: невырожденный полупроводник

F Е

" ' 2nm*

kT \з/2

p = N

e ^ .

Nv==2

^ .

(29>34)

и полностью вырожденный полупроводник

8π / 2т*j \з/2

Ρ = Ύ\4γ) (29.35)

. Резюме § 28, 29

1. Концентрация электронов η и дырок ρ определяется в виде

интеграла по зоне Бриллюэна от функции распределения:

п = п(г, 0= J А

> к. О.Лж, (29.1р)

(М

р = р(г, $ Ы

> ОЛк· (29.2р)

(

κ)

2. Функция распределения Ферми —Дирака для электронов

и дырок зависит от энергии и температуры, поэтому для вычисле-

ни я концентрации электронов и дырок необходимо перейти от интег-

рирования по объему зоны Бриллюэна к интегрированию по энер-

гии в пределах зоны энергии. Для этого вводится понятие плотно-

сти состояний N (£), представляющее собой число состояний в еди-

ничном интервале энергии на единичный объем кристалла. Ν (Е)

определяется условием

dS = N (Ε) dE = άτ

/8π

. (29.3ρ)

Функция Ν (Ε) определяется формой изоэнергетических поверх-

ностей.

3. При квадратичной зависимости энергии от квазиимпульса

для Ν (Е) у минимума энергии Е

имеем

N(E) = 2[-

ij (Ε

—

)

(29.4ρ)

и у максимума энергии Ε

имеем

Ν(Ε) = 2 (-у*) (E

- Еуп. (29.5р)

4. Эффективная масса для плотности состояний т% связана с тен-

зором эффективной массы т* и числом Μ эквивалентных экстрему-

мов энергии:

ml = (УИ^ШаШз)

. (29.6р)

178

Если

экстремум энергии лежит в центре зоны Бриллюэна, так что

IfUl, ·" поверхности энергии сферические, то т2 = т*. .

5. Концентрации электронов и дырок определяются соответственно

следующими соотношениями:

(29.7р)

2 N

ρ=

ρΐ

Φι/2(η)

(29

8ρ)

где через N

и N

обозначено эффективное число состояний для

зоны проводимости и валентной зоны:

2nmbkT\ / mi \з/2- /т*\з/2

/ г

\з/2

(29.9р)

- N

= 2ly p—j =4,82· 10

(-^J Τ

—

6. Концентрации электронов и

дырок в невырожденном полу-

проводнике определяются выражениями:

n = N

e W , (29.11р)

р = Л^е (29.12р)

Произведение концентраций электронов и дырок в невырожден-

ном полупроводнике от положения уровня Ферми не зависит:

АЕ

пр = N

. (29.1 Зр)

Полупроводник называется невырожденным, если уровень Ферми

лежит ниже Е

или выше E

не менее чем на kT. Другими словами,

невырожденном полупроводнике уровень Ферми находится в запре-

щенной зоне.

7. Полупроводник называется полностью вырожденным, если

Уровень Ферми лежит внутри зоны энергии на расстоянии не менее

ъкТ от экстремального значения энергии. Если уровень Ферми выше

не менее чем на 5kT, то концентрация электронов не зависит

0т

температуры

8π /2т*\з/2

" = "3 [-WJ СF-EcF*

. (29.14р)

179

а концентрация дырок определяется выражением (28.12р). Если уро.

вен ь Ферми ниже Ε

не менее чем на 5kT, то концентрация дырок

не зависит от температуры:

8л /2т*

Л 3/2

-F)W, (29.15р)

а концентрация электронов определяется выражением (29. lip).

8. Для вырожденных полупроводников независимо от закона дис-

персии

'·• $ (

29Л6

Р)

(

где V

~объем зоны Бриллюэна, ограниченный поверхностью Ферми.

Для сферических поверхностей энергии =

n=^-

Kh (29.17р)

а радиус сферы Ферми

Кр=(3п

п)

. (29.18р)

9. Для закона дисперсии Кейна при малых к из (28.53) и (29.18р)

следует:

η = i (i)

3/2

FW (Ε

+ F)W (29.19p)

8π

/2m®* \ з/2

/ ^ \з/2

«=з(т) ^(n-^J · (

°Ρ)

§ 30. УРАВНЕНИЕ ЭЛЕКТРОНЕЙТРЛЛЬНОСТИ

Выражения для пир позволяют вычислять концентрацию элек-

тронов и дырок при условии, что известно положение уровня Ферми.

Однако уровень Ферми сам зависит от температуры и концентрации

носителей заряда. Его положение может сильно меняться при вве-

дении примесей, создающих локализованные состояния. Это естест-

венно, поскольку уровень Ферми определяет распределение электро-

нов по состояниям. Вводя примесь, создаем в запрещенной зоне

локализованные состояния, в которых могут находиться как элек-

троны, так и дырки. Перераспределение электронов по состояниям

при создании дискретных уровней в .запрещенной зоне регулируется

посредством изменения положения уровня Ферми.

Для вычисления величины F служит уравнение, которое обычно

называется уравнением электронейтральности, имеющее простой

и наглядный физический смысл. Прежде всего, предположим, что

в полупроводнике .имеются донорная и акцепторная примеси с кон-

центрациями ;У

и N

. В результате термической ионизации в полу-

180