Kelter P., Mosher M., Scott A. Chemistry. The Practical Science
Подождите немного. Документ загружается.

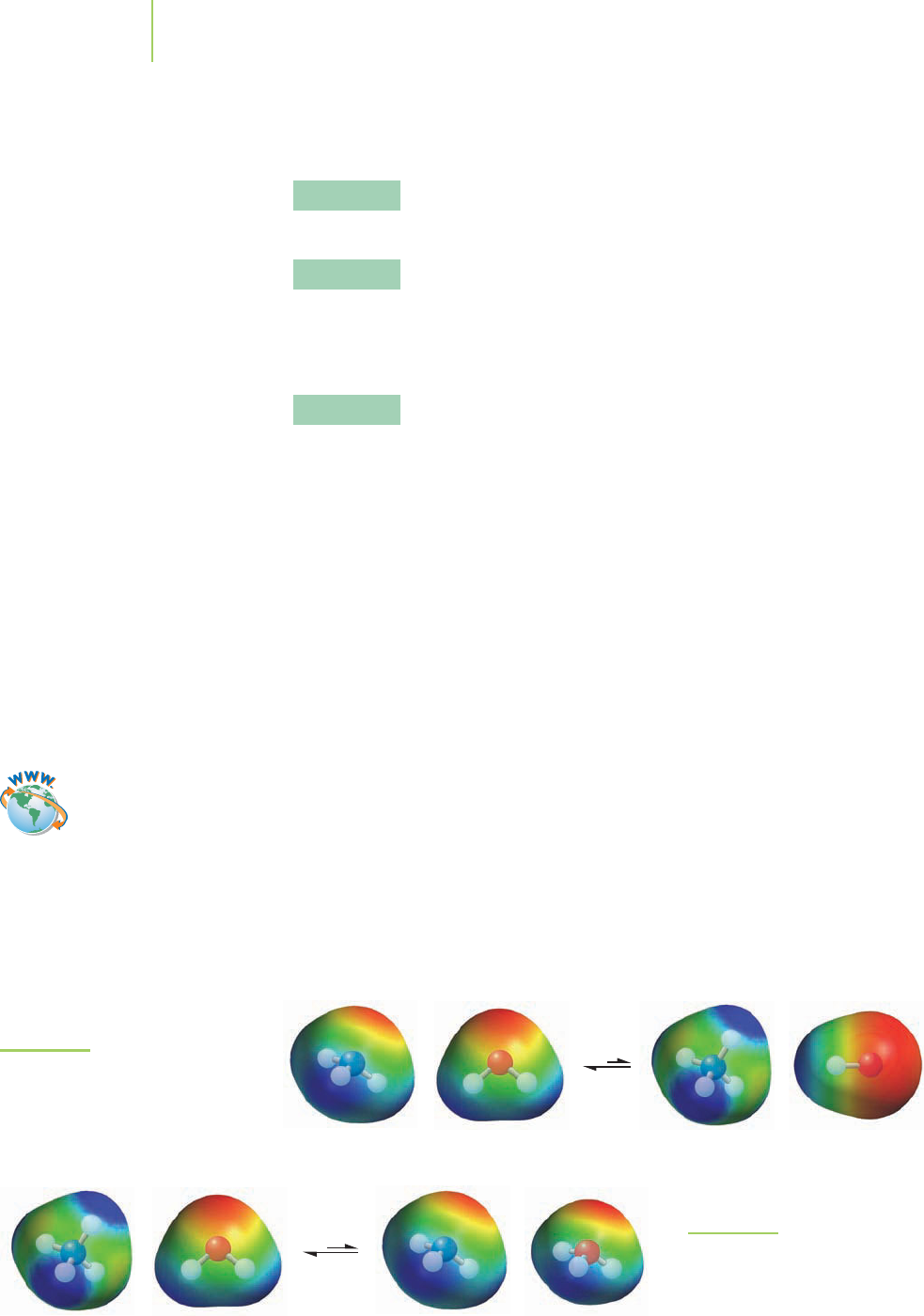
FIGURE 18.2
Addition of NH
4
+
shifts the
equilibrium of reaction 1 to the left.
in water to give the ammonium ion (NH
4
+
) with chloride (Cl
−
) as a spectator
ion. The key reactants in the buffer are NH
4
+
,NH
3
, and H
2
O. Their specific reac-
tions are given below.
Reaction 1: Ammonia, a weak base, reacts with water.
NH
3
(aq) + H
2
O(l)
NH
4
+
(aq) + OH
−
(aq) K
b
= 1.8
×
10
−5
Reaction 2: Ammonium ion, the conjugate acid of ammonia, reacts with
water.
NH
4
+
(aq) + H
2
O(l)
NH
3
(aq) + H
3
O
+
(aq) K
a
= 5.6
×
10
−10
(Recall from Section 17.7 that K
a
= K
w
/K
b
for NH
3
.)
Reaction 3: Water undergoes autoprotolysis.
2H
2
O(l)
H
3
O
+
(aq) + OH
−
(aq) K
w
= 1.0
×
10
−14
The last reaction has a relatively small equilibrium constant, so its contribu-
tion to the pH of the solution is unimportant. Judging by their respective
equilibrium constants, the base, ammonia, is stronger than its conjugate acid,
ammonium ion, so we expect reaction 1 to be dominant. The reaction produces
hydroxide ion, so we expect the solution to be basic.
The Impact of Le Châtelier’s Principle
on the Equilibria in the Buffer
Reaction 1 is producing NH
4
+
. However, in the buffer used to determine the
hardness of water, we already have a relatively high initial concentration of am-
monium ion ([NH
4
+
]
0
= 1.27 M). How will this affect the extent of reaction 1?
Le Châtelier’s principle (Sections 16.6 and 17.4) suggests that the presence of the
ammonium ion (a “common ion,” in this case) will shift the equilibrium of reac-
tion 1 to the reactants side, as shown in Figure 18.2. Reaction 1 will be drastically
suppressed because of the common-ion effect, an outcome of Le Châtelier’s
principle.
What about reaction 2? It is producing ammonia (NH
3
). However, the initial
concentration is quite high, [NH
3
]
0
= 8.44 M. As with reaction 1, the presence of
a large concentration of ammonia will shift the reaction to the left, the reactants
side (Figure 18.3). Reaction 2 will also be drastically suppressed because of the
common-ion effect, an outcome of Le Châtelier’s principle.
768 Chapter 18 Applications of Aqueous Equilibria
FIGURE 18.3
Addition of NH
3
shifts the
equilibrium of reaction 2 to the left.
Video Lesson: The Common Ion
Effect

The impact of reactions 1 and 2 being suppressed (claims that we will prove
after we solve for the pH of the buffer solution) is that we may assume that the
equilibrium concentrations of NH
3
and NH
4
+
are approximately equal to their ini-
tial concentrations.
[NH
3
]
≈
[NH
3
]
0
= 8.44 M and [NH
4
+
]
≈
[NH
4
+
]
0
= 1.27 M
Because of this assumption, we can solve for the pH of this buffer solution using
the mass-action expression derived from reaction 1, the hydrolysis of ammonia.
K
b
=
[NH
4
+
][OH
−
]
[NH
3
]
1.8
×
10
−5
=
(1.27)[OH
−
]
(8.44)
[OH
−
] = 1.2
×
10
−4
M
[H
+
] =
K
w
[OH
−
]
=
1.0 ×10
−14
1.2 ×10
−4
= 8.3
×
10
−11
M
pH = 10.08
Alternatively, we could have used the mass-action expression derived from reac-
tion 2 to solve for the pH of the solution, as we will discover in Exercise 18.1.
What about our claim that reaction 1 was suppressed by the presence of the
ammonium common ion? To show the impact of the common ion, let’s calculate
[OH
−
] in an 8.44 M NH
3
solution that has no NH
4
+
—in other words, not a
buffer, just a weak base—using the principles we learned in Chapters 16 and 17.
NH
3
(aq) + H
2
O(l)
NH
4
+
(aq) + OH
−
(aq) K
b
= 1.8
×
10
−5
K
b
=
[NH
4
+
][OH
−
]
[NH
3
]
1.8
×
10
−5
=
[NH
4
+
][OH
−
]
(8.44)
1.8
×
10
−5
=
x
2
8.44
x = [NH
4
+
] = [OH
−
] = 0.012 M
Our calculations reveal that the total hydroxide and ammonium ion concen-
trations, which are equal in this solution of weak base, are [OH
−
] = [NH
4
+
] =
0.012 M. Moreover, when we compare the hydroxide ion concentration of the buf-
fer, in which [OH
−
] = 1.2
×
10
−4
M, to the value we just calculated for the weak
base alone, we note that it is 100-fold less. The presence of the ammonium ion in
the buffer has suppressed reaction 1, the hydrolysis of ammonia, by 99%! If we were
to do a similar calculation with the ammonium ion, we would find that the buffer
suppresses the acid dissociation of NH
4
+
by over 99.99%. Le Châtelier’s principle
has again proved its worth as a formidable part of the chemist’s toolbox.
Our goal was to show how a mixture of these concentrations of ammonia and
ammonium ion results in a buffer solution with a pH of about 10. Exercise 18.1
shows the implications of using a slightly different approach to achieve the same
goal.
EXERCISE 18.1 Alternative Route to the pH of the Buffer
Instead of calculating the pH of the system using reaction 1, calculate the pH of the
buffer using reaction 2, the acid dissociation of the ammonium ion. What does your
result tell you about solving for the pH of a buffer?
First Thoughts
We still assert that the extent of reaction in a buffer system is negligible; the starting
position is the same as the equilibrium position, as shown by the equilibrium line
chart.
18.1 Buffers and the Common-Ion Effect 769
Video Lesson: CIA
Demonstration: Buffers in Action
The implication is that the starting and equilibrium concentra-
tions are essentially equal, so, as before,
[NH
3
]
≈
[NH
3
]
0
= 8.44 M
and
[NH
4
+
]
≈
[NH
4
+
]
0
= 1.27 M
Additionally, we are directed to solve the problem using reaction 2,
so we will use its mass-action expression to solve for [H
+
] and pH.
Solution
NH
4
+
(aq) + H
2
O(l)
NH
3
(aq) + H
3
O
+
(aq) K
a
= 5.6
×
10
−10
K
a
=
[NH
3
][H
3
O
+
]
[NH
4
+
]
5.6
×
10
−10
=
(8.44)[H
3
O
+
]
(1.27)
[H
+
] = 8.4
×
10
−11
M
pH = 10.08
Further Insights
Our answer is the same whether we use the mass-action expression for the hydroly-
sis of the base (ammonia) or the dissociation of its conjugate (ammonium ion).
This is a useful outcome that is a result of the common-ion effect of suppressing
both the acid reaction and the base reaction in the buffer. When working with
buffers, we may use either the acid dissociation or the conjugate base hydrolysis
mass-action expression, but we often work with the expression describing the reac-
tion of the stronger conjugate (the ammonia hydrolysis, in this case).
PRACTICE 18.1
Determine the pH of a buffer made from 1.50 M NH
3
and 3.50 M NH
4
+
.
See Problems 5 and 6.
EXERCISE 18.2 Practice Calculating the Initial pH of a Buffer
We have shown that an ammonia–ammonium ion buffer can have a pH of about
10. Are all buffers basic? To help answer the question, calculate the pH of a buffer
that contains 0.200 M each of acetic acid (CH
3
COOH) and its conjugate base, the
acetate ion (CH
3
COO
−
). It is interesting, but nonetheless coincidental, that the K
a
value for acetic acid is about the same as the K
b
value for ammonia.
First Thoughts
We said in the last exercise that we normally use the reaction and mass-action ex-
pression for the stronger conjugate when calculating the pH of the buffer. The rele-
vant conjugate reactions (using the shorthand form for the acid dissociation) and
equilibrium constants are
CH
3
COOH(aq)
H
+
(aq) + CH
3
COO
−
(aq) K
a
= 1.8
×
10
−5
CH
3
COO
−
(aq) + H
2
O(l)
CH
3
COOH(aq) + OH
−
(aq) K
b
= 5.6
×
10
−10
We will use the mass-action expression for the stronger conjugate, acetic acid. As
with other buffer systems, we recognize that both reactions are suppressed as we
have explained using Le Châtelier’s principle, so the equilibrium concentrations are
about equal to the initial concentrations of the respective components.
770 Chapter 18 Applications of Aqueous Equilibria
Reactants
E and S
Products
Solution
The mass-action expression for the reaction of acetic acid is
K
a
=
[CH
3
COO
−
][H
+
]
[CH
3
COOH]
Solving for [H
+
] and then pH, we find that
[H
+
] =
K
a
[CH
3
COOH]
[CH
3
COO
−
]
=
(1.8 ×10
−5
)(0.200)
(0.200)
= 1.8
×
10
−5
M
pH = 4.74
Further Insights
The ammonia–ammonium buffer has a basic pH, because the base, NH
3
, is the
stronger of the conjugate pairs. The acetic acid–acetate buffer system is acidic, be-
cause acetic acid is the stronger conjugate. This means that you can predict whether
a buffer is likely to be acidic or basic judging by the strength of each of the conju-
gates. The acetic acid–acetate buffer cannot have a pH of 10.
PRACTICE 18.2
Would you predict that a buffer prepared from the mixture of 0.300 M formic acid
(HCOOH) and 0.400 M sodium formate (HCOONa) would be acidic or basic?
Why? Prove your assertion by calculating the pH of this buffer. K
a
of formic acid =
1.8
×
10
−4
.
See Problems 21 and 22.
We have seen from this discussion that it is possible to determine the approx-
imate pH of a buffer. Extending that idea a step further, it is also possible to pick
a buffer that will be in the pH range we want by looking at whether the acid or the
base conjugate is the stronger. There is often much more to the selection of a
buffer than just pH, because we must consider factors such as whether the buffer
will interact with the substances we are studying and whether the buffer’s pres-
ence in the reaction system has any unintended health consequences. Once these
factors are taken into account, we need to know how to prepare the buffers in
order to use them.
HERE’S WHAT WE KNOW SO FAR
■
A buffer is a chemical system that is able to resist changes in pH.
■
A buffer consists of the combination of a weak acid and its conjugate base, or
of a weak base and its conjugate acid.
■
A buffer contains a high enough concentration of each conjugate that
acid–base equilibria are effectively suppressed, an outcome of Le Châtelier’s
principle.
■
A buffer will be acidic or basic, depending on which of the conjugates is the
stronger.
■
It is possible to calculate the pH of the buffer system by applying the princi-
ples of equilibrium and acid–base chemistry that we learned in the last two
chapters.
18.1 Buffers and the Common-Ion Effect 771
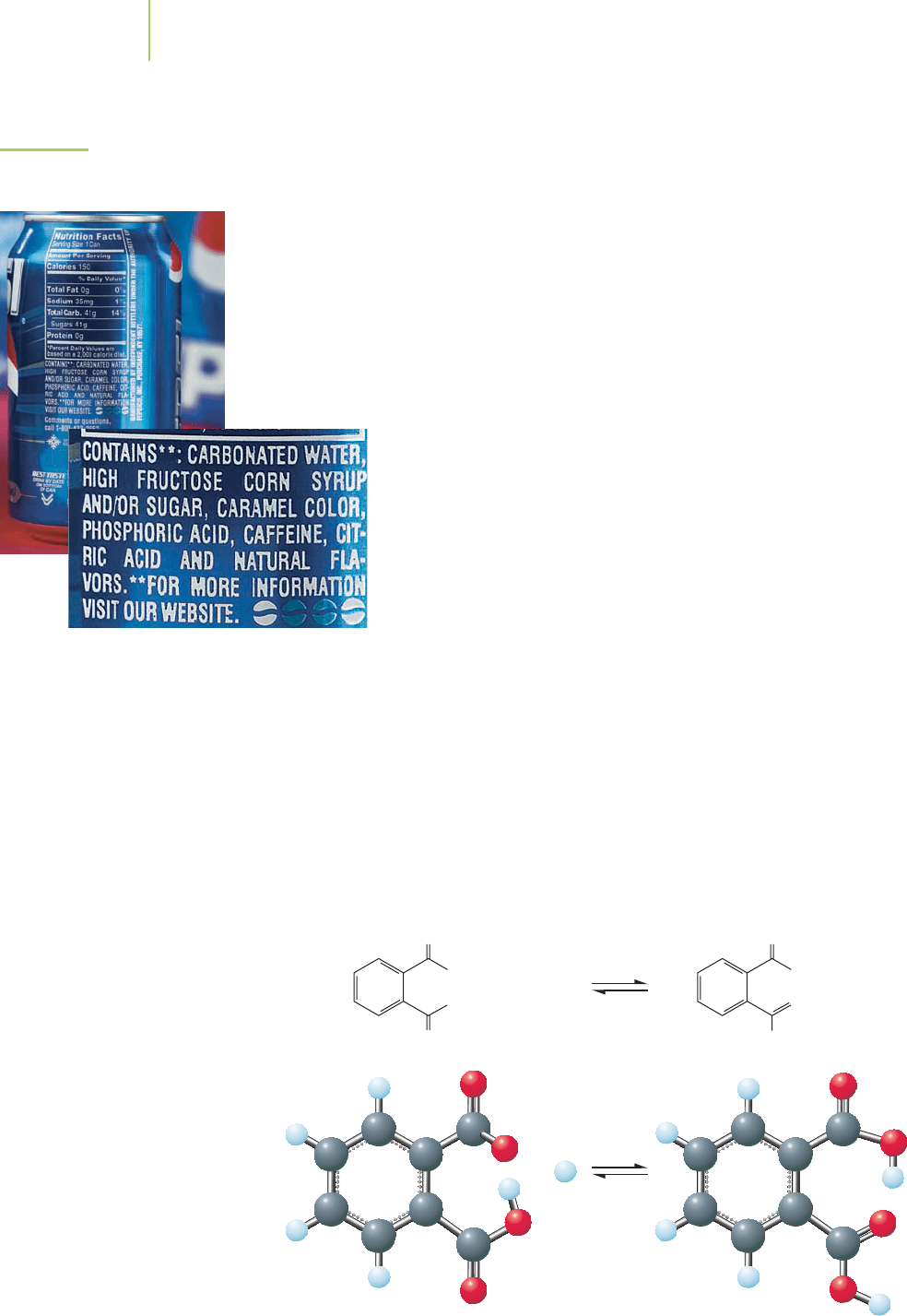
O
O
O
–
OH
O
O
OH
OH
+
+
H
+
FIGURE 18.4
Phosphoric acid is often found in
soft drinks.
Buffer Preparation
The chemical technician working in the food industry often uses a pH meter to
determine the acidity of the food that is being prepared. Sodas, for instance, often
have phosphoric acid added to them to provide a tart taste, and pH control is vital
(Figure 18.4).
One of the most common uses of a buffer solution is to calibrate pH meters.
This ensures that the reading on the meter accurately represents the pH of a
solution with which we are working. Recipes exist for the preparation of stan-
dard calibration buffer solutions. One source for these recipes is the The Phar-
macopeia of the United States of America/The National Formulary, a 2400-page
compendium of “standards and specifications for materials and substances that
are used in the practice of the healing arts.” Organized in 1884 and produced and
updated by medical and pharmaceutical experts ever since, the resulting Pharma-
copeia (“USP” for short) contains standard analysis procedures for a
great many substances.
The USP recipe to prepare calibration buffers in the range of 2.2
to 4.0 recommends using a solution of potassium hydrogen phtha-
late, or “KHP” (KHC
6
H
4
(COO)
2
), which dissociates when added to
water to form K
+
and HP
−
(HC
6
H
4
(COO)
2
). The conjugate acid of
this weak base, phthalic acid (“H
2
P”) is generated by addition of hy-
drochloric acid (a source of H
+
) to the HP
−
.
HP
−
(aq) + H
+
(aq)
H
2
P(aq)K ≈ 900
The equilibrium position (minimum free energy) of the reaction of
the weak base with the strong acid is so far toward the formation of
products that we can say the reaction is essentially complete. That is, although we
will normally write the reaction to show that it settles at some equilibrium point,
HP
−
(aq) + H
+
(aq)
H
2
P(aq)
we may also write it to show that the reaction is essentially complete,
HP
−
(aq) + H
+
(aq) n H
2
P(aq)
Suppose we wish to prepare a buffer with pH = 3.0, and assume that we want
the total concentration of phthalate species to be 0.0500 M. That is,
[H
2
P] + [HP
−
] = 0.0500 M
772 Chapter 18 Applications of Aqueous Equilibria

Once the proper ratio of conjugate acid to base is present, the buffer will be at
pH =3.00.
How do we find the proper ratio? How do we then find the final concen-
trations of H
2
P and HP
−
?
As has been true throughout these three chapters on equilibrium (Chapters
16–18), the answer lies in writing down the relevant equilibrium reaction and its
mass-action expression. For the phthalate buffer system, the important reaction
is the dissociation of phthalic acid (H
2
P) in water:
H
2
P(aq) + H
2
O(l)
HP
−
(aq) + H
3
O
+
(aq)
K
a
1
= 1.12
×
10
−3
We can write it using our shorthand form:
H
2
P(aq)
HP
−
(aq) + H
+
(aq)
K
a
1
= 1.12
×
10
−3
The mass-action expression for the reaction is
K
a
1
=
[HP
−
][H
+
]
[H
2
P]
Dividing both sides by [H
+
] gives us an expression for the ratio of base to acid:
K
a
1
[H
+
]
=
[HP
−
]
[H
2
P]
Solving, with the use of the pH = 3.00 ([H
+
] = 1.0
×
10
−3
M),
(1.12 ×10
−3
)
(1.00 ×10
−3
)
=
(1.12)
(1.00)
=
[HP
−
]
[H
2
P]
we find that the ratio of the base, HP
−
, to its conjugate acid, H
2
P, is 1.12 to 1.We’ll
call this Equation 1.
[HP
−
] = 1.12 [H
2
P] (Equation 1)
We said initially that we had set the sum of concentrations of the two species to
be a total of 0.0500 M. We’ll call this Equation 2.
[H
2
P] + [HP
−
] = 0.0500 M (Equation 2)
This gives us two equations (Equations 1 and 2) and two unknowns ([H
2
P] and
[HP
−
]). We can solve Equation 2 by substituting 1.12[H
2
P] in place of [HP
−
], as
allowed by Equation 1:
[H
2
P] + 1.12[H
2
P] = 0.0500 M
2.12[H
2
P] = 0.0500 M
[H
2
P] = 0.0236 M
[HP
−
] = 0.0500 M – 0.0236 M
[HP
−
] = 0.0264 M
Therefore, in order to obtain a buffer at pH = 3.00, we’ll have to make up a
solution that is 0.0236 M in H
2
P and 0.0264 M in KHP. We can check that these
quantities are reasonable by substituting back into the mass-action expression
and solving for [H
+
].
[H
+
] =
K
a
1
[H
2
P]
[HP
−
]
=
(1.12 ×10
−3
)(0.0236)
(0.0264)
[H
+
] = 1.00 × 10
−3
M
This concentration of H
+
would produce a solution with a pH = 3.00.
18.1 Buffers and the Common-Ion Effect 773
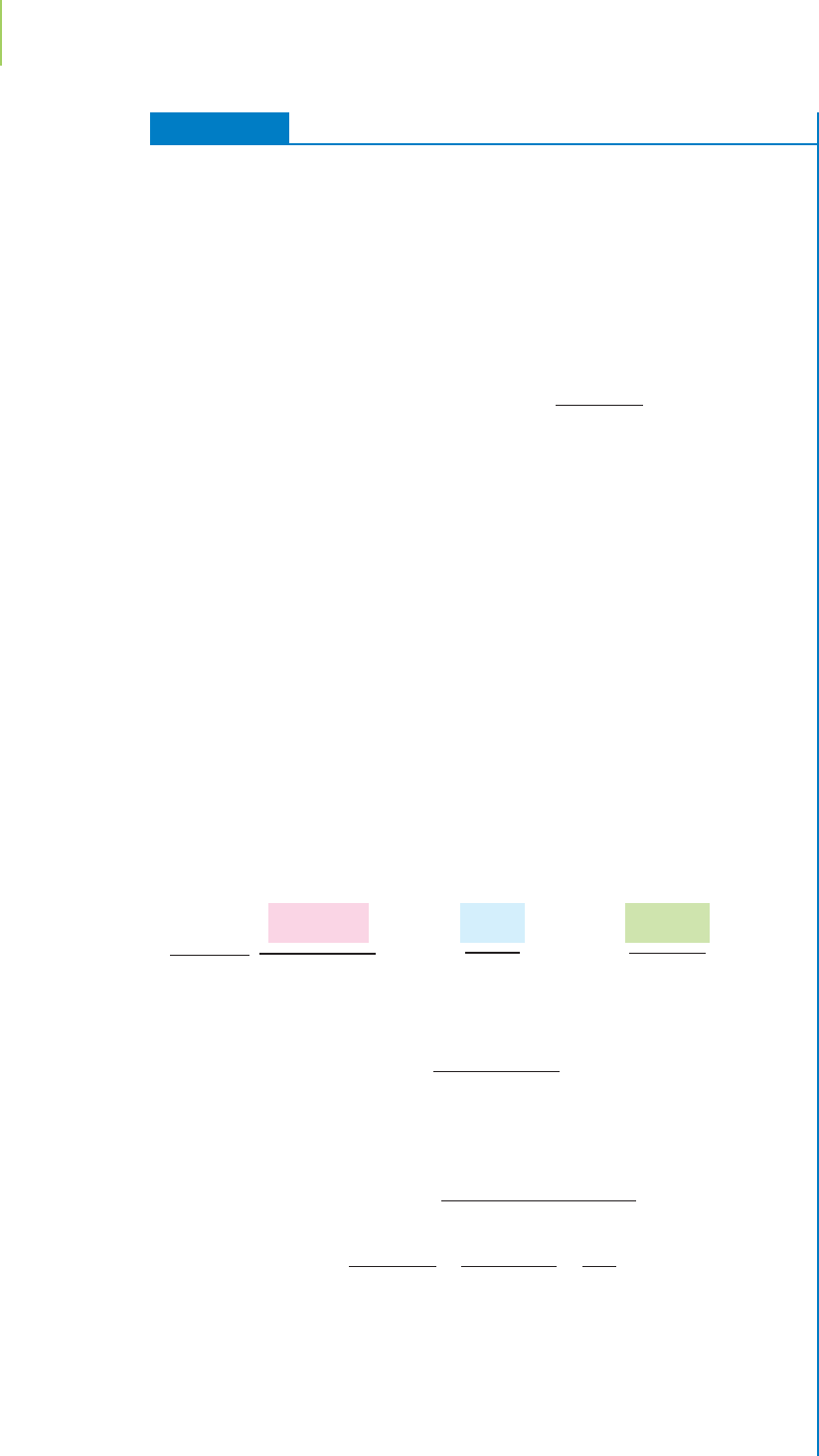
774 Chapter 18 Applications of Aqueous Equilibria
EXERCISE 18.3 Practice with Buffer Preparation
How many grams of sodium formate (HCOONa), molar mass =68.01 g/mol, must
be dissolved in a 0.300 M solution of formic acid (HCOOH), to make 400.0 mL of
a buffer solution with a pH = 4.60? Assume that the volume of the solution remains
constant when you add the sodium acetate.
First Thoughts
We are asked to find the mass of sodium formate needed to combine with formic
acid to prepare the buffer. Let’s develop a stepwise approach to the problem.
Step 1: As in prior examples involving buffers, we need to establish the ratio of the
concentrations of the acid and the conjugate base,
[HCOO
−
]
[HCOOH]
, needed to produce
a buffer with a pH = 4.60. To solve for the ratio of concentrations of acid and
conjugate base needed, we must first write the important processes that occur
in the solution. Two equilibria are important in this buffer system:
HCOOH(aq) + H
2
O(l)
H
3
O
+
(aq) + HCOO
−
(aq) K
a
= 1.8
×
10
−4
HCOO
−
(aq) + H
2
O(l)
HCOOH(aq) + OH
−
(aq) K
b
= 5.6
×
10
−11
As we discussed in Exercise 18.1, we may use either reaction to solve for the acid-
to-conjugate-base ratio.
Step 2: Knowing that the concentration of formic acid is 0.300 M, we can then
find the concentration of the conjugate base. Remember that the sodium salt will
completely dissociate in solution, leaving the formate anion (HCOO
−
) as the
conjugate base and Na
+
as the spectator ion.
Step 3: We may then convert from the concentration of formate (HCOO
−
) to the
number of moles of HCOO
−
in 400.0 mL of solution.
Step 4: Finally, we may convert from moles of formate (as the sodium formate
salt) to grams of sodium formate.
A flowchart of the process looks like this:
[HCOO
−
]
[HCOOH]
[HCOO
−
]
mol HCOO
−
g HCOONa
Step 1 Step 2 Step 3 Step 4
Solution
Step 1: K
a
=
[HCOO
−
][H
+
]
[HCOOH]
The pH of the solution is 4.60, so
[H
+
]
=2.51
×
10
−5
M. We are retaining an extra
figure because this is an intermediate calculation.
1.8
×
10
−4
=
[HCOO
−
](2.51 ×10
−5
)
[HCOOH]
[HCOO
−
]
[HCOOH]
=
1.8 ×10
−4
2.51 ×10
−5
=
7.17
1.00
The concentration of formate ion is about 7.2 times as great as the concentration
of formic acid.
Step 2:
[HCOO
−
]
= 7.17
×
[HCOOH]
[HCOO
−
]
= 7.17
×
0.300 M
[HCOO
−
]
= 2.15 M
n
mass-action
expression
volume
solution
molar mass
HCOONa
n
n
Alternatively, we could have combined steps 1 and 2 to find
[HCOO
−
]
directly by
substituting 0.300 M into the mass-action expression, as follows:
1.8
×
10
−4
=
[HCOO
−
](2.51 ×10
−5
)
0.300
[HCOO
−
]
= 2.15 M
Step 3:
2.15 mol HCOO
−
L solution
× 0.4000 L solution
=
0.860 mol
HCOO
−
= 0.860 mol HCOONa
Step 4: 0.860 mol HCOONa
×
68.01 g HCOONa
1 mol HCOONa
= 58 g HCOONa
Further Insights
Does it make sense that the buffer system should be acidic? Formic acid (HCOOH)
is stronger than its conjugate, so the acid dissociation reaction will dominate,
resulting in an acidic buffer solution. This is a reasonable conjugate pair to use to
prepare an acidic buffer solution. Our answer makes sense.
PRACTICE 18.3
How many grams of sodium formate (HCOONa) must be dissolved in a 0.150 M
solution of formic acid (HCOOH) to make 500.0 mL of a buffer solution with
pH = 3.95? Assume that the volume of the solution remains constant when you add
the sodium formate.
See Problems 17, 18, 25, and 26.
EXERCISE 18.4 More Practice with Buffer Preparation
How many milliliters of 0.200 M HCl must be added to 50.0 mL of a 0.200 M solu-
tion of NH
3
in order to prepare a buffer that has a pH of 8.60?
NH
3
+ H
2
O(l)
NH
4
+
+ OH
−
K
b
= 1.8
×
10
−5
First Thoughts
We have a solution of NH
3
. We need to add enough strong acid, in the form of HCl,
to convert NH
3
to NH
4
+
until the ratio of the weak base to its conjugate acid,
[NH
3
]
[NH
4
+
]
, will be the same as that in a pH 8.60 buffer.
As we think through a problem-solving strategy, let’s write down what we know
about the system.
■
The K
b
value for the hydrolysis of NH
3
is 1.8
×
10
−5
.
■
We know the mass-action expression for the formation of NH
4
+
from NH
3
.
■
We also know that there is 0.0100 mol of NH
3
initially present in the
solution:
0.0500 L NH
3
×
0.200 mol NH
3
LNH
3
solution
= 0.0100 mol NH
3
Step 1: What is the ratio of the weak base to the conjugate acid,
[NH
3
]
[NH
4
+
]
, in the
pH = 8.60 buffer ([H
+
] = 2.5
×
10
−9
M)? This ratio will be the first equation we
need to solve in order to find the amounts of NH
3
and NH
4
+
. The base hydrolysis
equation contains [OH
−
] rather than [H
+
]. We can solve for [OH
−
] from [H
+
]
and K
w
. We are keeping an extra figure in for the intermediate calculation.
[OH
−
]
=
K
w
[H
+
]
=
1.00 ×10
−14
2.51 ×10
−9
= 3.98
×
10
−6
18.1 Buffers and the Common-Ion Effect 775

We can then set up our mass-action expression to solve for
[NH
3
]
[NH
4
+
]
.
NH
3
(aq) + H
2
O(l)
NH
4
+
(aq) + OH
−
(aq) K
b
= 1.8
×
10
−5
K
b
=
[NH
4
+
][OH
−
]
[NH
3
]
K
b
[OH
−
]
=
[NH
4
+
]
[NH
3
]
Inverting both sides of the equation, we get
[OH
−
]
K
b
=
[NH
3
]
[NH
4
+
]
Step 2: The sum of the moles of NH
3
and NH
4
+
in the final solution must equal
the initial 0.100 mol of NH
3
used to prepare the original solution because we are
changing the NH
3
to NH
4
+
, not getting rid of any from the reaction flask. This is
the second equation we need to solve to find the amounts of NH
3
and NH
4
+
.
mol NH
4
+
+ mol NH
3
= 0.0100 mol
Step 3: Finally, we can find how much 0.200 M HCl will be needed to react with
our original 0.100 mol of NH
3
to generate the proper number of moles of NH
4
+
.
Solution
Step 1: Finding the ratio of
[NH
3
]
[NH
4
+
]
in the solution.
[OH
−
]
K
b
=
[NH
3
]
[NH
4
+
]
Substituting for [OH
−
] and
K
b
yields
3.98 ×10
−6
1.8 ×10
−5
=
0.221
1.00
=
[NH
3
]
[NH
4
+
]
Because the volume of the buffer solution is the same for NH
3
and NH
4
+
,we
can work with moles rather than molarity (the liters cancel out on top and
bottom).
mol NH
3
= 0.221 × (mol NH
4
+
)
Step 2: Finding moles of NH
4
+
and NH
3
so that the sum equals 0.0100 mol.
mol NH
4
+
+ mol NH
3
= 0.0100 mol
mol NH
4
+
+ [0.221 × (mol NH
4
+
)] = 0.0100 mol
1.221 × (mol NH
4
+
) = 0.0100 mol
mol NH
4
+
= 0.00819 mol
mol NH
3
= 0.00181 mol
As a check of your work, you will find that substituting these values back into the
mass-action expression will give you K
b
.
Step 3: Finding how many milliliters of 0.200 M HCl we need to add to produce
0.00819 mol of NH
4
+
from NH
3
.
0.00819 mol HCl ×
1 L HCl solution
0.200 mol HCl
×
1000 mL HCl solution
1 L HCl solution
= 41 mL HCl solution
776 Chapter 18 Applications of Aqueous Equilibria

Further Insights
Although we used the base hydrolysis of ammonia to get the initial conjugate
acid–base ratio, we could have used the acid ionization of ammonium just as well,
because we are dealing with a buffer solution. If we had done this, the solution in
step 1 would have looked like this:
NH
4
+
(aq) + H
2
O(l)
NH
3
(aq) + H
3
O
+
(aq)
K
a
=
[K
w
]
[K
b
]
=
(1.0 ×10
−14
)
(1.8 ×10
−5
)
= 5.56 × 10
−10
(We retain an extra figure in K
a
, which we would drop at the end of the calculation.)
K
a
=
[NH
3
][H
3
O
+
]
[NH
4
+
]
[K
a
]
[H
3
O
+
]
=
[NH
3
]
[NH
4
+
]
[NH
3
]
[NH
4
+
]
=
(5.56 ×10
−10
)
(2.51 ×10
−9
)
=
0.221
1.00
mol NH
3
= 0.221 (mol NH
4
+
)
This agrees with the answer we got in step 1.
PRACTICE 18.4
How many milliliters of 0.10 M HCl must be added to 25.0 mL of a 0.2000 M solu-
tion of NH
3
to prepare a buffer that has a pH of 8.80?
See Problems 11, 12, 27, and 28.
In practice, even fairly dilute buffers with fairly low conjugate concentrations
(not far above their equilibrium constants) will have pH values similar to those
with equal ratios of higher conjugate concentrations. If the buffer is too dilute,
other factors cause the pH to move toward neutrality.
The Henderson–Hasselbalch Equation: We Proceed,
But with Caution
We have seen how the mass-action expression is used to find the approximate
ratio of base to acid in a buffer. In 1902, seven years before Peter Sørenson coined
the term pH, a Massachusetts physician named Lawrence Joseph Henderson,
who was studying buffers in blood, published work relating [H
+
] to the acid and
base concentrations in a buffer. For an acid, HA, and its conjugate base, A
−
,
Henderson noted that [H
+
] =
K
a
[HA]
[A
−
]
,as we showed in Exercise 18.2 for the acetic
acid–acetate ion buffer system. Written a slightly different way for visual clarity,
this is
[H
+
] = K
a
[HA]
[A
−
]
= K
a
[weak acid]
[conjugate base]
Note the relationship between the acid and the base. The acid is a weak acid, and
the base is the conjugate base of that weak acid. In 1916 K.A. Hasselbalch (pro-
nounced “hassle-back”), a physiologist at the University of Copenhagen, used
18.1 Buffers and the Common-Ion Effect 777
Video Lesson: The
Henderson–Hasselbalch
Equation
