Kelter P., Mosher M., Scott A. Chemistry. The Practical Science
Подождите немного. Документ загружается.

This is more reasonable than our initial answer of pH = 8 (after all, an acid
solution should be acidic, not basic!), and it also shows the importance of
Le Châtelier’s principle as well as the autoprotolysis of water.
pH of Weak Acid Solutions
As we noted in Section 14.5, lactic acid (HC
3
H
5
O
3
) is produced in our muscle
cells when we work too strenuously to maintain aerobic respiration (respiration
in the presence of sufficient oxygen). Recent evidence shows that contrary to
long-time assumptions, lactic acid is a normal product of metabolism and not
the barrier to athletic performance that was previously assumed. Lactic acid can
be prepared commercially and is used in products ranging from biodegradable
polymers to a spray to help extend the shelf life of beef strips. Its wide range of bi-
ological applications makes lactic acid a useful prototype for our discussion
about the pH of weak acids.
Let’s determine the pH of a 0.10 M solution of lactic acid. We considered the
steps in accomplishing this task in Chapter 16. This is an equilibrium problem,
and we may solve it using the same principles that we use to solve any other
equilibrium problem.
Steps in Solving for the pH of a Weak Acid in Aqueous Solution
Step 1: Determine the equilibria, and the resulting species, that are in the
solution.
There are two important equilibria occurring simultaneously in this solution:
the ionization of lactic acid (HC
3
H
5
O
3
, written here for simplicity as HL) and
the autoprotolysis of water.
HL(aq)
H
+
(aq) +L
−
(aq) K
a
= 1.38 ×10
−4
H
2
O(l)
H
+
(aq) +OH
−
(aq) K
w
= 1.00 ×10
−14
Step 2: Determine the equilibria that are the most important contributors to
[H
+
] in the solution.
As we discussed previously, an acid that is much stronger than water will sig-
nificantly depress the ionization of water in accordance with Le Châtelier’s prin-
ciple. Let’s assume that this holds true for a relatively concentrated solution of
the weak acid so that we can safely neglect the autoprotolysis of water as a con-
tributor of H
+
. We will test this assumption later.
Step 3: Write the equilibrium expression for the important contributors to [H
+
]
(which usually means just the weak acid).
K
a
=
[L
−
][H
+
]
[HL]
Step 4: Set up a table of the initial and equilibrium concentrations of each
pertinent species.
Weak acids are called weak because the extent of their ionization is normally
quite small. As a first approximation, we may assume that “x” is far less than
0.100 M, or, equivalently, that [HL] ≈ [HL]
0
. We do this because it greatly sim-
plifies our problem solving, but we will also test this assumption later. The as-
sumption will generally work if K
a
is less than about 10
−2
×[HL]
0
. In the present
problem, 10
−2
×0.10 = 1 ×10
−3
. Our K
a
of 1.38 ×10
−4
is less than that, so our
assumption is probably valid.
738 Chapter 17 Acids and Bases
Check
assumptions.
Make a table.
Write the mass-
action expression.
Determine the
equilibria in solution.
Determine the most
important equilibrium.
Solve for x; then
determine concentrations.
Application
STEP 1
Tutorial: Calculating pH of Weak
Acid and Base Solutions
HL
H
+
+ L
−
initial 0.10 M 0 M 0 M
change −x +x +x
equilibrium 0.10 − x +x +x
assumptions 0.10 +x +x
Step 5: Solve for the estimated concentration of each species.
1.38 × 10
−4
=
x
2
0.10
x = [H
+
] = [C
3
H
5
O
3
−
] = 3.7 × 10
−3
M
[HC
3
H
5
O
3
] = 0.10 − 3.7 × 10
−3
= 0.096 M
Step 6: Check our assumption that the extent of ionization of lactic acid is neg-
ligibly small.
This is done using the “5% rule,” which we introduced in Section 16.5. Also as
discussed in that section, you can ignore the 5% simplification if you want to
program your calculator to solve the quadratic equation in all cases. We present
the 5% rule there, and here, because it shows that it is possible to use our un-
derstanding of chemistry to arrive at a solution strategy that is straightforward
whether or not a programmable calculator is available.
17.4 Determining the pH of Acidic Solutions 739
Check
assumptions.
Make a table.
Determine the
equilibria in solution.
Determine the most
important equilibrium.
Write the mass-
action expression.
Solve for x; then
determine concentrations.
STEP 5
Write the mass-
action expression.
Solve for x; then
determine concentrations.
Check
assumptions.
Make a table.
Determine the
equilibria in solution.
Determine the most
important equilibrium.
STEP 6
Write the mass-
action expression.
Solve for x; then
determine concentrations.
Check
assumptions.
Calculate
pH
Make a table.
Determine the
equilibria in solution.
Determine the most
important equilibrium.
STEP 7
If less than 5% of the original amount of the weak acid ionizes, this is con-
sidered “negligible.” If more than 5% ionizes, then we must take this into ac-
count in our problem solving during Step 4. We will show how this is done
below. What percentage of the lactic acid has ionized?
% dissociated =
[C
3
H
5
O
−
3
]
HC
3
H
5
O
3
×
100% =
3.7 ×10
−3
0.10
×
100% = 3.7%
We can consider the ionization to be negligible because less than 5% of the orig-
inal acid reacted to form products.
Step 7: Solve for the pH of the solution.
pH =−log[H
+
] =−log(3.7 × 10
−3
M) = 2.43
Remember that the number of significant figures after the decimal point in the
pH is equal to the number of significant figures in the pre-exponential term. Be-
cause the pre-exponential term is 3.7, we use two figures after the decimal point
(“.43”). The pH = 2.43.
EXERCISE 17.11 pH of a Weak Acid
We have mentioned aqueous hydrofluoric acid (HF) several times in this chapter,
and we have found it to be a weak acid, K
a
=7.2 × 10
−4
. It is employed in the chem-
ical industry to produce alkylated (see Section 12.3) compounds in gaso-
line and fluorocarbons used, for example, in refrigerants. Calculate the pH
in a 1.0 × 10
−3
M HF solution.
First Thoughts
Our understanding of equilibrium tells us that even though the specific exercise is
different from the one we just went over together, the questions that we ask about
the chemical system remain the same, and therefore our approach is consistent.
We understand our chemical system (and, in doing so, get a reasonable answer for
the pH) by asking the right questions.
Solution
Step 1: Equilibria in solution.
The two important equilibria in the solution are the ionization of HF and the au-
toprotolysis of water.
HF(aq)
H
+
(aq) + F
−
(aq) K
a
= 7.2 × 10
−4
H
2
O(l)
H
+
(aq) + OH
−
(aq) K
w
= 1.00 × 10
−14
Step 2: Determine the equilibria that are the most important contributors to [H
+
]
in the solution.
We will assume that the HF ionization is the only important contributor to
[H
+
] in solution because its K
a
value is far greater than the K
w
value of water.
Step 3: Write the equilibrium expression for the important contributors to [H
+
].
K
a
=
[F
−
][H
+
]
[HF]
740 Chapter 17 Acids and Bases

Step 4: Table of concentrations.
HF
H
+
+ F
−
initial 1.0 × 10
−3
M 0 M 0 M
change −x +x +x
equilibrium 1.0 × 10
−3
− x +x +x
assumptions 1.0 × 10
−3
+x +x
Although we assume that the ionization of HF is negligibly small (that is, “x”
is essentially irrelevant compared to 1.0 × 10
−3
M), the assumption is hazardous
because K
a
, 7.2 × 10
−4
, is not less than about 10
−2
× [HF]
0
(= 1.0 × 10
−5
M).
Rather, it is nearly equal to [HF]
0
! Let’s determine the implications of making
the assumption.
Step 5: Solve.
7.2 × 10
−4
=
x
2
1.0 ×10
−3
x = [H
+
] = [F
−
] = 8.5 × 10
−4
M
Step 6: Check our assumption of negligible ionization.
% dissociated =
[F
−
]
[HF]
×
100% =
8.5 ×10
−4
1.0 ×10
−3
× 100% = 85%
Wow! This is certainly not negligible compared to 5%, so we may not claim that
the ionization of HF is negligibly small. We must solve the following equation,
which uses the “equilibrium”row of the ICEA table, rather than the “assumptions”
row.
7.2 × 10
−4
=
x
2
1.0 ×10
−3
− x
We can set up the quadratic equation by multiplying K
a
, 7.2 × 10
−4
, by [HF],
1.0 × 10
−3
− x,to give
x
2
= 7.2 × 10
−7
− 7.2 × 10
−4
x
Setting the equation = 0 so we may solve for x yields
x
2
+ (7.2 × 10
−4
x) − 7.2 × 10
−7
= 0
As we discussed in Section 16.5, we can solve the quadratic equation by substitut-
ing values for a, b, and c in the quadratic formula:
x =
−b ±
√
b
2
− 4ac
2a
In the present exercise,
a = 1 b = 7.2 × 10
−4
c =−7.2 × 10
−7
Substituting into the quadratic formula yields
x =
−7.2 ×10
−4
±
(7.2 ×10
−4
)
2
− 4(1)(−7.2 × 10
−7
)
2(1)
x =
−7.2 ×10
−4
± 1.843 ×10
−3
2
x = [H
+
] = [F
−
] = 5.62 × 10
−4
M ≈ 5.6 × 10
−4
M
[HF] = 1.0 × 10
−3
− x = 1.0 × 10
−3
− (5.62 × 10
−4
)
= 4.38 × 10
−4
≈ 4.4 × 10
−4
M
17.4 Determining the pH of Acidic Solutions 741

Step 7: Solve for the pH of the solution.
pH =−log[H
+
] =−log(5.62 × 10
−4
) = 3.25
We can check our math by substituting back into the mass-action expression.
K
a
=
(5.62 ×10
−4
)
2
4.38 ×10
−4
= 7.2 × 10
−4
Our answer is confirmed.
Further Insights
We often assume, on the basis of the low value of K
w
, that the autoprotolysis of
water is unimportant, and we assumed that in Step 2 above. Did this make sense?
What is the hydrogen ion concentration due to the autoprotolysis of water? It is
equal to the hydroxide ion concentration due to water. That is,
[H
+
]
water
= [OH
−
]
water
Also, water is the only source of hydroxide ion in this weak acid solution. Therefore,
[OH
−
]
total
=
K
w
[H
+
]
total
=
1.00 ×10
−14
5.62 ×10
−4
= 1.8 × 10
−
11
M=[OH
−
]
water
=[H
+
]
water
This is so much smaller than 5.62 × 10
−4
M that it can be safely neglected. Our
decision to neglect the autoprotolysis of water as a source of H
+
ions made sense.
PRACTICE 17.11
What is the pH of a 0.250 M acetic acid solution (K
a
= 1.8 × 10
−5
)?
See Problems 39–50.
pH of a Mixture of Monoprotic Acids
If you ingest some vinegar, 3% acetic acid, does it significantly change the pH of
your HCl-containing stomach? This question falls within the general topic of the
pH of a mixture of acids that differ greatly in strength. Consider a solution that is
0.50 M HCl and 0.90 M acetic acid (CH
3
COOH), K
a
= 1.8 × 10
−5
. To solve for
the pH of the mixture, we employ our usual approach. The relevant equilibria in
the solution are
HCl(aq)
H
+
(aq) + Cl
−
(aq) K
a
>1
CH
3
COOH(aq)
H
+
(aq) + CH
3
COO
−
(aq) K
a
= 1.8 × 10
−5
H
2
O(l)
H
+
(aq) + OH
−
(aq) K
w
= 1.00 × 10
−14
This says that there are three sources of hydrogen ion: HCl, CH
3
COOH, and
H
2
O. We can write this in equation form:
[H
+
]
total
= [H
+
]
HCl
+
[H
+
]
CH
3
COOH
+
[H
+
]
H
2
O
The hydrochloric acid is a substantially stronger acid than either the acetic acid or
the water and is present in a concentration that is large enough so that we may
make the assumption that neither the acetic acid nor the water ionizes signifi-
cantly. In fact, the presence of hydrogen ion (the common ion!) from HCl further
suppresses the acetic acid and water ionization in accordance with Le Châtelier’s
principle.
[H
+
]
total
= [H
+
]
HCl
≈ 0.50 M
We will test this assumption later.
What is the hydrogen ion contribution due to the acetic acid? We know that
[H
+
]
total
=0.50 M. We also know that the [H
+
] contributed by the acetic acid will
742 Chapter 17 Acids and Bases

be essentially equal to the [CH
3
COO
−
]. The concentration of acetic acid at equi-
librium will be essentially equal to its initial concentration.
[CH
3
COOH] = 0.90 M
[H
+
]
acetic acid
= [CH
3
COO
−
] =“x”
We can use the mass-action expression for acetic acid ionization to solve for
[H
+
]
acetic acid
.
K
a
=
[CH
3
COO
−
][H
+
]
[CH
3
COOH]
1.8 ×10
−5
=
x(0.50)
0.90
x = [CH
3
COO
−
] = [H
+
]
acetic acid
= 3.2 × 10
−5
M
This shows that acetic acid is not a significant contributor to the hydrogen ion
concentration of the solution, and although we did not quantify it here, the water
is even less important. Further, if we had had an aqueous solution of only 0.90 M
CH
3
COOH (without the HCl), the equilibrium concentration of the acetate ion,
[CH
3
COO
−
], would have been
K
a
=
[CH
3
COO
−
][H
+
]
[CH
3
COOH]
1.8 × 10
−5
=
x
2
0.90
x = [H
+
] = [CH
3
COO
−
] = 4.0 × 10
−3
M
This is nearly 100 times higher than the equilibrium acetate ion concentration of
3.2 × 10
−5
M in the HCl solution. This confirms what we said previously, that
“the presence of hydrogen ion (the common ion!) from HCl further suppresses
the acetic acid and water ionization in accordance with Le Châtelier’s principle.”
The main message to keep in mind from this discussion is that when you cal-
culate the pH of a mixture of acids, you must look for the dominant equilibrium.
This will determine the pH of the solution.
17.5 Determining the pH of Basic Solutions
We have noted in this chapter the impact of acids and bases on ourselves and our
world. A useful, though perhaps unfortunate, example concerns tobacco, which,
according to the World Health Organization, prematurely kills well over 4 million
people worldwide each year. Tobacco companies have used scientists’ under-
standing of acid–base chemistry to increase by a factor of 100 the amount of
nicotine that leaves solid burned tobacco particles and enters the gas phase to be
absorbed by the lungs. The two important compounds involved in this chemistry
are the nicotine itself (C
10
H
14
N
2
) and ammonia, both of which
are bases (see Figure 17.15). We will look at how ammonia can
be used to increase the amount of gaseous nicotine that enters
the lungs of smokers. As a first step in our analysis, we need to
see how and why ammonia acts as a base.
Ammonia (NH
3
) has many applications, including those
shown in Table 17.1. It is the fourth-ranked industrial chemical,
with 10.8 billion kg produced in 2004. Ammonia is quite solu-
ble in water, acting as a weak base. Using the Arrhenius model
of base behavior, it supplies hydroxide ions to the solution.
17.5 Determining the pH of Basic Solutions 743
Application
N
CH
3
N
Nicotine
N
H
H
H
Ammonia
FIGURE 17.15
Ammonia and nicotine are both bases.

Ammonia is typical of many bases in that it has an unshared pair of electrons
on the nitrogen atom that can accept a proton from, in this case, the water mole-
cule, as shown in the illustration.
Ammonia is considered a weak base because the K
b
value is much less than 1.
On the other hand, Group IA hydroxides, such as NaOH and KOH, completely
dissociate in water (K
b
>> 1) to supply hydroxide ion and are considered strong
bases.
NaOH(s) → Na
+
(aq) + OH
−
(aq)
The solubility of Group IIA hydroxides increases from the essentially insoluble
Be(OH)
2
to the more soluble (0.01 M) Ca(OH)
2
to the still more soluble (up to
0.1 M) Ba(OH)
2
. Soluble Group IIA hydroxides, such as Ca(OH)
2
,are strong
bases like their Group IA counterparts, but they supply two moles of hydroxide
for every mole of base that dissolves.
Ca(OH)
2
(s)
Ca
2
+
(aq) + 2OH
−
(aq)
Drawing on your understanding of equilibrium (that is, what are the right ques-
tions to ask in order to understand what happens in the solution?) and your sense
of the pH scale, try the following two exercises dealing with the pH of a strong
base solution and of the weakly basic ammonia solution. Even though we are now
looking at bases rather than acids, the equilibrium processes and the thinking
involved are largely the same.
EXERCISE 17.12 pH of a Strong Base
Calculate the pH of a 0.60 M aqueous solution of KOH.
First Thoughts
As a strong base, KOH completely dissociates. This is consistent with the behavior
of Group IA and soluble Group IIA hydroxides.
KOH(s) → K
+
(aq) + OH
−
(aq) K >> 1
The other acid–base reaction that occurs in solution is the autoprotolysis of water,
although it is unimportant as a source of OH
−
because the K value is so small com-
pared to that of the strong base.
H
2
O(l)
H
+
(aq) + OH
−
(aq) K
w
= 1.0 × 10
−14
Solution
Potassium hydroxide is a strong base and will completely dissociate in aqueous
solution.
KOH(s) → K
+
(aq) + OH
−
(aq)
[OH
−
] = 0.60 M
pOH = 0.22; pH = 13.78
Further Insights
Does the answer make sense? We expect the pH to be quite high, analogous to the
very low pH of a strong acid, so our answer makes sense. In addition, the pH is
744 Chapter 17 Acids and Bases
NH
3
(aq)
++
H
2
O(l)NH
4
+
(aq) K
b
= 1.8 × 10
–5
OH
–
(aq)
++

considerably higher than with the same concentration of ammonia, a weak base.
This is shown in the next exercise.
PRACTICE 17.12
Calculate the pH of a 1.06 M solution of NaOH. (Hint: It is possible to have aque-
ous solutions with a pH below 0 or above 14, although the actual pH is somewhat
difficult to measure.)
See Problems 38 and 54.
EXERCISE 17.13 pH of a Weak Base
Determine the pH of a 0.600 M solution of ammonia.
First Thoughts
We may proceed as with any equilibrium problem, by listing the equilibria that
occur in solution.
NH
3
(aq) + H
2
O(l)
NH
4
+
+ OH
−
(aq) K
b
= 1.8 × 10
−5
H
2
O(l)
H
+
(aq) + OH
−
(aq) K
w
= 1.0 × 10
−14
The autoprotolysis of water is insignificant compared to the hydrolysis of ammonia.
In fact, the OH
−
produced by the ammonia reaction will further depress the auto-
protolysis of water (via Le Châtelier’s principle), so the OH
−
and H
+
due to water
will be less than in neutral solution, as discussed previously. The only relevant equi-
librium expression is
K
b
=
[NH
+
4
][OH
−
]
[NH
3
]
Solution
We set up the table of concentration changes in the usual fashion.
1.8 × 10
−5
=
x
2
0.600
x = [NH
4
+
] = [OH
−
] = 3.3 × 10
−3
M
pOH = 2.48; pH = 11.52
Further Insights
Were we justified in neglecting “x”? The percent dissociation was
3.3 ×10
−6
0.600
×
100% = 0.5%
Our assumption was valid. Were we justified in neglecting the autoprotolysis of
water as a source of hydroxide ions? The only source of hydrogen ions in this solu-
tion is the autoprotolysis of water. If pH = 11.52, then [H
+
]
water
= 3.0 × 10
−12
M.
This also equals [OH
−
]
water
, and this is insignificant compared to 3.3 × 10
−3
M, the
total [OH
−
]. Does our answer make sense? To the extent that our pH reflects a mod-
erately basic solution, our answer does make sense.
NH
3
NH
4
+
+ OH
−
initial 0.600 M 0 M 0 M
change −x +x +x
equilibrium 0.600 − x +x +x
assumptions 0.600 +x +x
17.5 Determining the pH of Basic Solutions 745
PRACTICE 17.13
Calculate the pH of a 0.500 M solution of dimethylamine, (CH
3
)
2
NH, K
b
=
5.9 × 10
−4
.
See Problems 51–53, 55, and 56.
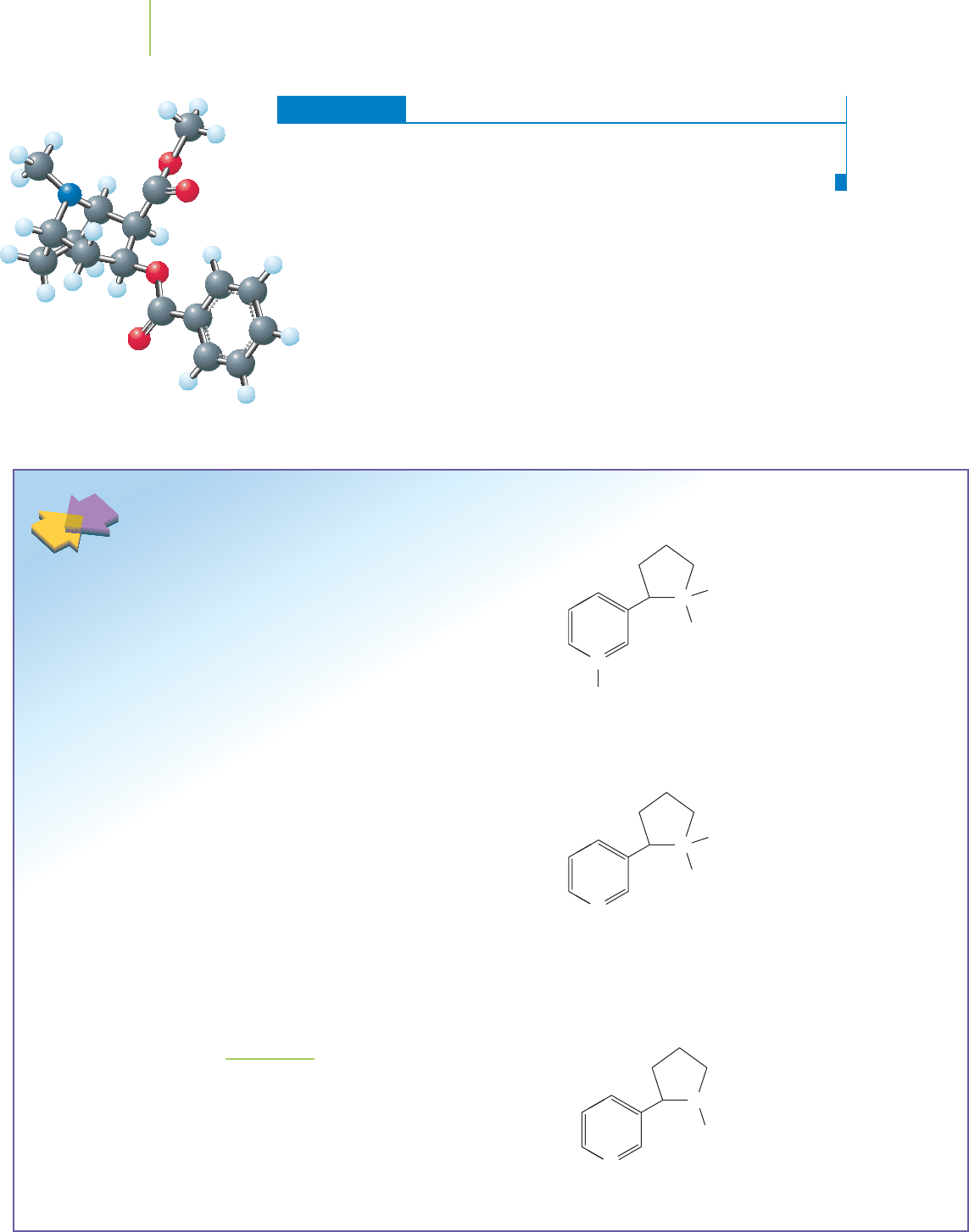
One class of alkaloids, ephedrines, are used as dietary supplements to
help in weight loss, to enhance body building, and to increase the user’s en-
ergy level. In doses of more than 8 mg per serving, the compounds are con-
sidered dangerous for routine use. Another of the alkaloids, cocaine, has a
severe psychological impact. It can be made basic to create the free-base
form called “crack.”
746 Chapter 17 Acids and Bases
“Crack” cocaine
Nicotine can exist in three forms, depend-
ing on the pH of its environment (see Fig-
ure 17.16). Below pH 3, it is in the diprotonated form.
Between about pH 3 and pH 8, most of it is in the monopro-
tonated form.
If the pH is above 8, most of the nicotine exists in
the volatile “free-base” form, which readily evaporates at the
temperature of burning tobacco. This free-base is effectively
absorbed by the lung tissue. Ammonia is added to tobacco
leaves to raise the pH, making available more free-base nico-
tine for inhalation. The Food and Drug Administration has
also determined that pH levels have been manipulated in
smokeless tobacco products. The products for new users are
at a relatively low pH, so there is not that much free-base
nicotine available. Smokeless tobacco for “experienced” users
has a higher pH, which leads to a higher level of nicotine
absorption.
Nicotine is an
alkaloid, one of many nitrogen-containing
bases found in vegetables and other plants. Table 17.7 lists
the structures and uses of some alkaloids. You might recog-
nize the names of some of the compounds in the table. They
often have a substantial impact on the central nervous sys-
tem and brain.
Issues and Controversies
Nicotine and pH Control in Cigarettes
H
CH
3
N
H
N
pk
a
1
3.12
(a)
N
N
H
CH
3
pk
a
2
8.02
(b)
N
N
CH
3
(c)
FIGURE 17.16
The three forms of nicotine. (a) The form that predom-
inates below pH 3.12. (b) The form that predominates
between pH 3.12 and 8.02. (c) The form that pre-
dominates above pH 8.02. This “free-base” form is
readily vaporized and absorbed into the lungs when
the cigarette burns.
HO
H
PO
H
O
O
O
HO
H
PO
H
O
17.6 Polyprotic Acids
Our theme is impact—the impact of acids and bases on the chemical industry, on
our environment, and on ourselves. Phosphoric acid (H
3
PO
4
) fits well with that
theme. It is different from other acids we have mentioned thus far, because it is a
polyprotic acid. Like all polyprotic acids, phosphoric acid contains more than one
acidic hydrogen. The structure of this
triprotic acid (three acidic hydrogen atoms)
acid is shown in Figure 17.17, with its three acidic hydrogen atoms highlighted.
The acid is produced from “phosphate rock,” which is largely composed of fluo-
roapatite (Ca
5
(PO
4
)
3
F) and other compounds containing iron, calcium, silicon,
aluminum, and fluorine.
17.6 Polyprotic Acids 747
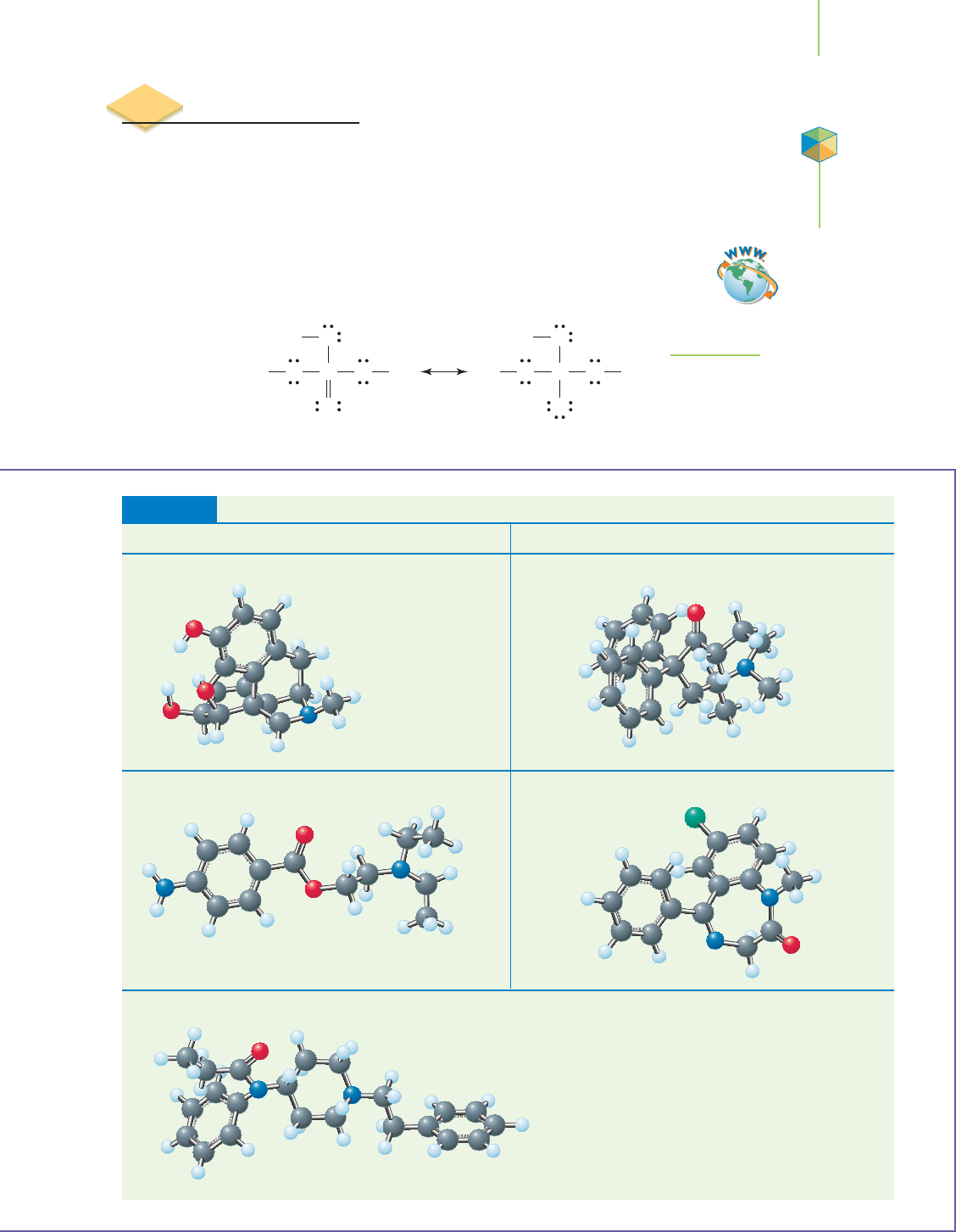
Structures and Uses of Selected Alkaloids
Structure Common Use Structure Common Use
Morphine Addictive pain reliever Methadone Therapy for heroin addiction
Procaine Local anesthetic Valium Tranquilizer
Fentanyl Anesthetic in most surgical procedures
TABLE 17.7
Application
C
HEMICAL ENCOUNTERS:
Production and Uses
of Phosphoric and
Sulfuric Acids
FIGURE 17.17
Phosphoric acid (H
3
PO
4
) is triprotic acid because
it contains three acidic hydrogen atoms.
Video Lesson: Examining
Polyprotic Acids
