Kelter P., Mosher M., Scott A. Chemistry. The Practical Science

Подождите немного. Документ загружается.

EXERCISE 15.5 How Long Will It Take?

Diazinon crystals are sprinkled around a home’s foundation to kill and repel ants

from the home. How long will it take for the diazinon to decompose, assuming ﬁrst-

order kinetics, to 25% of its original concentration in the soil? (From Table 15.2, the

half-life of diazinon is 4.0 × 10

days.)

First Thoughts

The problem doesn’t state the original concentration of the diazinon in the soil.

However, we don’t need to know the concentration to determine the answer, be-

cause we have the ratio of initial concentration to ﬁnal concentration (that is,

[diazinon]

=0.25[diazinon]

Solution

Using the half-life, we ﬁrst calculate the rate constant for the reaction:

1/2

0.693

4.0 ×10

days =

0.693

k = 0.0173 day

−1

Note that the unit of the rate constant is reciprocal days and that we retain an extra

ﬁgure in the value because we will use the data in the next part of the calculation. If

25% of the diazinon remains, then



0.25[diazinon]

[diazinon]



=−(0.0173 day

−1

ln 0.25 =−0.0173 day

−1

−1.386 =−0.0173 day

−1

t = 8.0 × 10

days

Further Insight

There is an alternative method by which we can calculate the answer. One half-life

reduces the original concentration by 50% (50% = 0.5 =

⁄2). Two half-lives reduce

the concentration to 25% (

⁄2

⁄2 =

⁄4). Three reduce the concentration to 12.5%

(

⁄2

⁄2 =

⁄8). Because we want to know the time required for the reaction to

reduce the concentration of starting material to 25% of the initial concentra-

tion, we need two half-lives (4.0

days + 4.0

days =8.0

days).

Therefore,for a ﬁrst-order process, the fraction remaining, [A]

/[A]

equals 2

−n

where n

= number of half-lives. For example, for n = 3 half-lives, [A]

/[A]

−3

or 0.125.

PRACTICE 15.5

What is the length of time you would have to wait for alachlor to decompose to 25%

of its original value? ...to 6.25%? ...to 0.001%?

See Problems 27 and 28.

Other Rate Laws

Not all reactions follow ﬁrst-order kinetics. Other orders do exist, even noninte-

ger orders. Reactions that take place on metal surfaces typically follow zero-order

kinetics. Hydrogenation of vegetable oils, the decomposition of ammonia on a

tungsten wire, and the reaction of N

O with oxygen in your car’s catalytic con-

verter are reactions on metal surfaces. They follow zero-order kinetics.

638 Chapter 15 Chemical Kinetics

Diazinon

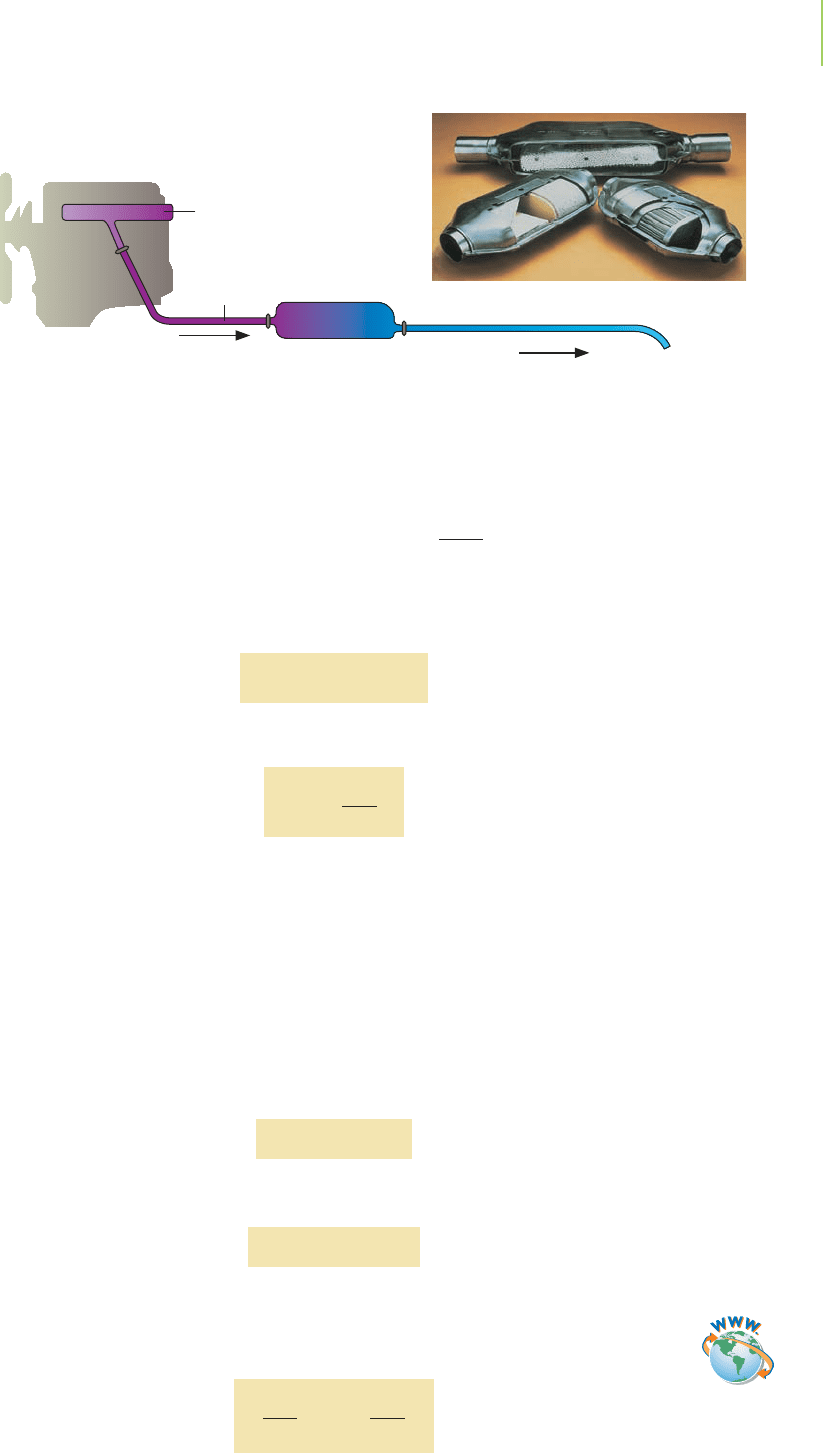
In a zero-order reaction, the rate law does not depend on the concentration of

any of the compounds in the reaction. The rate of the zero-order reaction is con-

stant. No matter what the original concentration happens to be, the reaction

always proceeds at the same rate.

Rate of disappearance of A =−

[A]

t

Rate = k[A]

= k

The integrated zero-order rate law, determined by integrating the rate law over

time, for a zero-order reaction is different from the integrated ﬁrst-order rate law:

[A]

=−kt + [A]

Substituting 0.5[A]

for the concentration of A at time t, we can rearrange the

equation to get the formula for the half-life of the zero-order reaction:

1/2

[A]

The half-life of a zero-order reaction directly depends on the initial concentra-

tion of the reactant. Larger concentrations of the reactant will mean a larger half-

life for the reaction. Note that the rate of a zero-order reaction is constant but that

the half-life depends on the initial concentration of reactant. For example, con-

sider a zero-order reaction where the rate constant k = 2.5

−4

M/s. When

[A]

=1.00 M, the half-life of the reaction is 2000 s. If [A]

=0.25 M, the half-life

of the reaction is 500 s. The rate of the reaction (rate = k) is a constant, but the

half-life changes as the concentration changes.

The

second-order rate law can be more complicated, because there are two

cases that ﬁt the deﬁnition of a second-order reaction. In one of those cases, the

reaction is second order in only one reactant:

Rate = k[A]

In the other case involving a second-order rate law, the reaction could be ﬁrst

order in two different species:

Rate = k[A][B]

In second-order reactions with only one reactant, the integrated rate law is

determined using the method we have explored for the zero-order and ﬁrst-order

reactions. After integration and rearrangement, the

integrated second-order rate

law

takes the form

[A]

= kt +

[A]

15.3 Changes in Time—The Integrated Rate Law 639

Exhaust

manifold

Exhaust

pipe

Tailpipe

Catalytic

converter

CO, NO, O

, N

Catalytic converters

catalyze the reaction

of N

O into N

.The

reaction is zero order.

Video Lesson: Second-Order

Reactions

The half-life of this type of second-order reaction can be determined by assum-

ing that the concentration of A at some time, t, is equal to one-half the initial con-

centration ([A]

= 0.5[A]

). Simplifying the equation gives

1/2

k[A]

The half-life for a second-order reaction (involving only one compound in the rate

law) is inversely dependent on the initial concentration of the reactant. Smaller ini-

tial concentrations of the reactant will mean a longer half-life for the reaction.

If the second-order reaction contains two species in the rate law, the inte-

grated rate law becomes much more complicated. In fact, the math gets so com-

plicated that chemists typically manipulate the experimental conditions to reduce

the amount of calculation. Consider the reaction of one of the components of

smog with ozone:

NO(g) + O

(g) n NO

(g) + O

(g)

Rate = k[NO][O

]

The reaction is ﬁrst order in NO, ﬁrst order in O

, and second order overall.

To calculate the concentration of a reactant, determine the rate constant, or

ﬁnd the time required to reach a certain concentration with this type of rate law,

we conduct the reaction with a relatively small concentration of one of the reac-

tants and a very large concentration of the other.

What effect does this have on the

rate law?

Because one of the concentrations is very large, any change in its con-

centration is negligible, and we can assume that its concentration remains constant

through the course of the reaction. An analogy is having someone who is rich spend

$1 in a day (decreasing to 50 cents after one half-life!) from a fortune of $1 bil-

lion. The change is hardly noticeable. The fortune is essentially constant.

Someone who had only $10, however, would notice the effect of spending $1 im-

mediately. Having the concentration of one component much larger than that of

the other reduces the rate law to a much simpler form. For example, if we per-

form the reaction with 0.100 M NO and 0.001 M O

, the concentrations of the

species after the reaction is complete can be determined:

]

= 0.001 M − 0.001 M = 0.000 M

[NO]

= 0.100 M − 0.001 M = 0.099 M ≈ 0.100 M

The O

is consumed in the reaction, but the concentration of NO is only slightly

affected. We can make the assumption that the concentration doesn’t change.

Because the ﬁnal concentration of NO has essentially remained constant, it can

be combined with the rate constant.And the rate equation for the reaction can be

reduced to

Rate = k [NO][O

] = k [NO]

]

and, because k = k [NO],

Rate = k [O

]

where k is the new rate constant. What is the order of our new rate law? Because

of our choice of the initial concentrations, the kinetics for this reaction has taken

on the form of a ﬁrst-order rate law. Because of our modiﬁcation, we say that this

is a

pseudo-ﬁrst-order rate equation.

We can do this manipulation with any reaction. By increasing the concentra-

tion of a particular reactant to a very large value, any order of a rate law can be

simpliﬁed to a pseudo-ﬁrst order rate equation. This enables us to study reactions

no matter what order they appear to be. We must remember, however, that any

modiﬁcation of the rate equation means that the new rate constant is not the

same rate constant as in the original reaction.

640 Chapter 15 Chemical Kinetics

15.4 Methods of Determining Rate Laws 641

FIGURE 15.13

Roundup herbicide contains glyphosate.

The general herbicide is sold for use on

farms and in removing unwanted weeds

around the yard.

HERE’S WHAT WE KNOW SO FAR

■

The integrated rate laws enable researchers to calculate one of four things

about a reaction (rate, rate constant, initial concentration, or ﬁnal concentra-

tion) if three of these are known.

■

The half-life of a reaction indicates the time required for the reaction to reach

50% completion.

■

Modifying a second-order reaction by using a large concentration of one of

the reactants reduces the integrated rate law to a pseudo-ﬁrst-order rate law.

15.4 Methods of Determining Rate Laws

Glyphosate herbicides are absorbed through the foliage of weeds, inhibiting a

plant’s ability to make new amino acids. Because these herbicides react relatively

quickly with water (

1/2

< 7

days), the rate of their biological reaction in plants is

important. Weed scientists study the rates of amino acid inhibition and environ-

mental degradation in order to suggest modiﬁcations to improve glyphosate

effectiveness (Figure 15.13). The greatest beneﬁt of the glyphosate herbicides is

attributable to their rapid degradation in the environment. The rapid degrada-

tion means this class of herbicide causes less harm to the environment than other

herbicides. The rates of the degradation of these compounds have been measured

by experiment, and the overall rate laws have been determined from those

experiments.

We, too, can use the information from a chemical reaction to obtain the ﬁnal

rate law for a reaction. The ﬁrst of two commonly used procedures that we will

consider is the

method of initial rates. In this appraoch, we measure and compare

initial rates rather than comparing instantaneous rates later in the reaction. We

use initial rates to determine the rate law because we can precisely measure and

control the starting concentrations of the reactants and precisely identify the

time for the reaction to reach a given point. In addition, limited side reactions

(reactions that make products other than what we’re interested in), rapid deter-

mination of the rate, and a well-deﬁned time period make the comparison of

multiple reactions experimentally straightforward.

We’ll use as our example the reaction of nitrogen monoxide, NO(g), with

oxygen to make nitrogen dioxide, NO

(g), a component of smog. We can

measure the initial rate of this reaction as we change the concentrations of

both NO(g) and O

(g). We conduct three separate reactions with different

concentrations of reactants, measure the initial rate, and complete the table

on the next page. Note that we have carefully chosen our starting concentra-

tions to keep one reactant the same in two experiments while doubling the

other reactant.

2NO(g) + O

(g) n 2NO

(g)

We can determine the rate law for this reaction by assuming that the rate is

based solely on the two reactants in the equation. We write

Rate = k[NO]

]

where n and m are the orders of the two reactants. If we compare the rate of the

third reaction to the rate of the second reaction, in which [NO] is constant and

] changes, the equation simpliﬁes dramatically. To do this, let’s divide the rate

law for the third experiment into the rate law for the second experiment.

rate

k[NO]

]

k[NO]

]

Application

Glyphosate

642 Chapter 15 Chemical Kinetics

Next, we add the values from the table to the equation. Then we simplify the

equation. Although the value of the rate constant, k, is not known, it should be

the same in both reactions:

1.13 ×10

−1

M·s

−1

5.64 ×10

−2

M·s

−1

k(0.0252)

(0.0250)

k(0.0252)

(0.0125)

2 =

(0.0250)

(0.0125)

2 = 2

m = 1

Why did we divide the second equation by the third? When one of the reactant

concentrations is held constant ([NO], in this case) and the other concentration

([O

]) is doubled, the effect on the rate is due only to the change in [O

]. This

effect is related to a power of 2 and reveals the order of the second reactant

(m = 1). To continue, we divide the third rate law by the ﬁrst because [O

] is con-

stant while [NO] changes, so the effect on the rate is due only to the change in [NO].

We substitute concentrations and solve:

5.64 ×10

−2

M·s

−1

1.41 ×10

−2

M·s

−1

k(0.0252)

(0.0125)

k(0.0126)

(0.0125)

4 =

(0.0252)

(0.0126)

4 = 2

n = 2

We are nearly ready to write the rate law for the reaction because we know the

order of the reactants. We are missing only the rate constant. We can solve for k

by choosing one of the experiments we’ve completed and substituting the con-

centrations into the rate law. Solving for the rate constant, we obtain

Rate = k[NO]

]

1.41 ×10

−2

= k(0.0126)

(0.0125)

k = 7.11 × 10

−2

·s

−1

The method of initial rates requires that we can obtain and compare the ini-

tial rates of reactions. We need at least three reactions to solve for two unknown

orders. And in every case, we’ve used experimentally determined data to calculate

the rate law for the reaction.

Note that the units for the rate constant are different depending on the order

of the rate law. Speciﬁcally, the units are M

−(order −1)

·s

−1

Automobile exhaust produces nitrogen compounds

that react with oxygen.

[NO] [O

] Initial Rate

Experiment (M)(M)(M/s)

1 0.0126 0.0125 1.41 × 10

−2

2 0.0252 0.0250 1.13 × 10

−1

3 0.0252 0.0125 5.64 × 10

−2

EXERCISE 15.6 Initial Rates

The reaction of Cl

with NO occurs at a very rapid pace. Use the data in the table

below to determine the rate law for the reaction. Then calculate the rate constant.

2NO(g) + Cl

(g) n 2NOCl(g)

15.4 Methods of Determining Rate Laws 643

Initial Rate

Experiment [NO]

(M) [Cl

]

(M)(M/min)

1 0.10 M 0.10 M 0.18

2 0.10 M 0.20 M 0.36

3 0.20 M 0.20 M 1.45

Solution

The rate law for the reaction can be determined by using the method of initial rates.

The overall rate law, based on the reaction, is

Rate = k[NO]

[Cl

]

The order of the reaction with respect to NO is

Rate 3

Rate 2

1.45 M·min

−1

0.36 M·min

−1

k(0.20)

(0.20)

k(0.10)

(0.20)

1.45

0.36

(0.20)

(0.10)

4 = 2

m = 2

The order of the reaction with respect to Cl

Rate 2

Rate 1

0.36 M·min

−1

0.18 M·min

−1

k(0.10)

(0.20)

k(0.10)

(0.10)

0.36

0.18

(0.20)

(0.10)

2 = 2

n = 1

The overall rate law and the value for the rate constant can then be calculated. Note

that the rate is still expressed in concentration per unit time. Also note that while the

orders in this rate law equal the coefﬁcients in the equation for this example, this is

not always true. We will deal with this in Section 15.6.

Rate = k[NO]

[Cl

]

k =

0.18

(0.10)

= 1.8 ×10

−2

·min

−1

PRACTICE 15.6

Use the initial rates for the reaction of carbon monoxide (CO) with hemoglobin (Hb)

to determine the rate law and the rate constant.What is the overall order of the reaction?

See Problems 57–60, 66, and 67.

Experiment [Hb] (M) [CO] (M) Initial Rate (M/s)

1 2.21 × 10

−6

M 1.00 × 10

−6

M 0.619 × 10

−6

2 4.42 × 10

−6

M 1.00 × 10

−6

M 1.24 ×10

−6

3 4.42 × 10

−6

M 3.00 × 10

−6

M 3.71 ×10

−6

644 Chapter 15 Chemical Kinetics

The second method for determining the rate law of a reaction has us examine

only one reaction instead of a series of reactions. In this

method of graphical

analysis

(also known as the method of integrated rate laws), we plot how the con-

centration of a reactant changes with time. Although this method does require us

to measure the rate of the reaction as it proceeds over a long time period, little

mathematical manipulation of the data is needed to determine the rate law. Var-

ious versions of the plot can be quickly constructed in order to establish a linear

relationship between time and a measure of concentration that conﬁrms one of

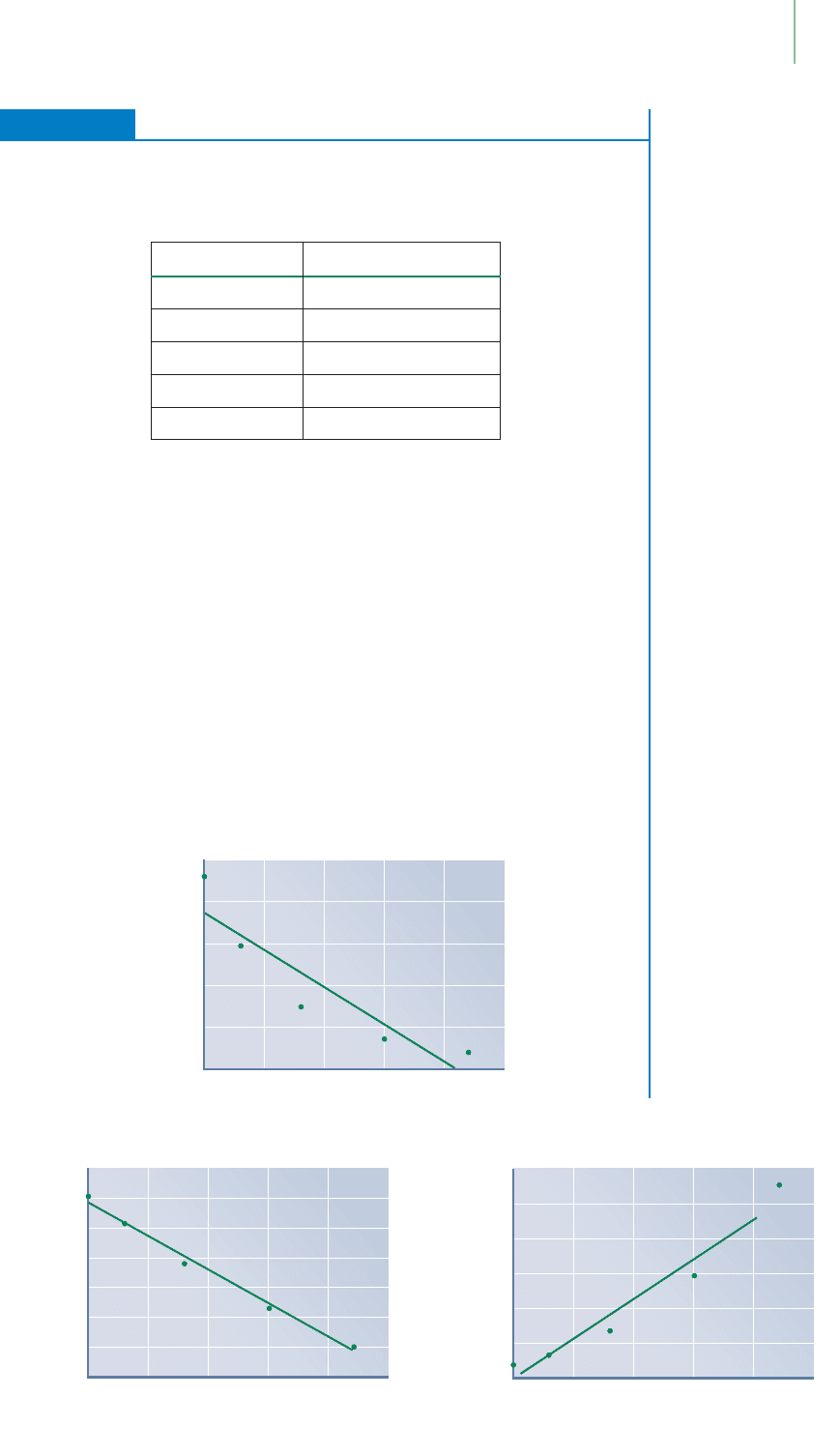
our common rate laws. Figure 15.14 displays plots of zero-order, ﬁrst-order, and

second-order reactions. Each is a linear relationship that is derived from the inte-

grated rate law. If our data are linear when plotted in one of these ways, it suggests

that the data ﬁt that model. Computer-based data acquisition can also help us to

do statistical analyses to determine the model that best ﬁts the data.

Here are the possible outcomes that we will consider:

■

The zero-order reaction produces a linear plot when the concentration of re-

actant is plotted against time. The slope of the line is equal to –k.

■

The ﬁrst-order reaction produces a linear plot when the natural logarithm (ln)

of the concentration of reactant is plotted against time. The slope in this case

is also equal to the negative of the rate constant, –k.

■

The second-order reaction produces a linear relationship when the reciprocal

concentration is plotted against time. The slope, which is equal to the rate con-

stant, is positive in this case.

If the concentration of a reactant is followed as a function of time, this is the best

method to use in determining the rate law. By graphing the data in three different

ways, we can determine the overall order of the reaction (zero order, ﬁrst order,

or second order).

Time (seconds)

Zero-Order Reaction

[A] (M)

0.05

0.1

0.15

0.2

0.25

1 6 11 16 21

Slope = –k

Time (seconds)

Slope = –k

Slope = k

Second-Order Reaction

ln[A]

0.05

0.1

0.15

0.2

0.25

1 6 11 16 2

Time (seconds)

First-Order Reaction

1/[A]

0.05

0.1

0.15

0.2

0.25

1 6 11 16 2

FIGURE 15.14

A linear relationship exists for the data if time is

plotted versus [A] for zero-order reactions, versus

ln[A] for ﬁrst-order reactions, and versus 1/[A] for

second-order reactions. Note that the slope of the

line is equal to the negative of the rate constant for

zero-order and ﬁrst-order plots. The slope of the

second-order plot is equal to the rate constant.

Visualization: Rate Laws

First Thoughts

We must plot the data for each of the three models we have discussed: zero order,

ﬁrst order, and second order. If might be useful to add two columns to your table for

ln[atrazine] and 1/[atrazine], respectively.

Solution

Using a graphical analysis software package (or three sheets of graph paper), we plot

the data on three different graphs. In the ﬁrst, the concentration is plotted versus

time, the second relates the ln[atrazine] versus time, and the third illustrates

1/[atrazine] versus time. Examination of the results leads us to the conclusion that

the middle plot—the one that relates ﬁrst-order kinetics—is the appropriate graph.

We choose this one because the data points seem to lie closest to the line of best ﬁt,

without being systematically curved. The reaction must be ﬁrst order overall and

ﬁrst order in atrazine (the reactant).

EXERCISE 15.7 Determining the Reaction Order

The decomposition of atrazine in the presence of titanium dioxide has been studied

and the rate of the reaction measured. Plot the data shown in the table, and deter-

mine whether the reaction follows zero-order, ﬁrst-order, or second-order kinetics.

15.4 Methods of Determining Rate Laws 645

Time (hours)

First-Order Reaction

ln[n]

–13.0

–12.5

–12.0

–11.5

–11.0

–10.5

–10.0

–9.5

0 5 10 15 20 25

y = –0.1151x – 10.075

= 0.9913

[n]

Time (hours)

Zero-Order Reaction

5.0 × 10

–5

4.0 × 10

–5

3.0 × 10

–5

2.0 × 10

–5

1.0 × 10

–5

0 5 10 15 20 25

y = –2 × 10

–6

x + 4 × 10

–5

= 0.842

Time (hours)

Second-Order Reaction

0 5 10 15 20 25

1/[n]

3.0 × 10

2.5 × 10

2.0 × 10

1.5 × 10

1.0 × 10

5.0 × 10

y = 11261x – 522.33

= 0.9475

Time (h) [Atrazine] (M)

0 4.65 × 10

−5

3 2.98 × 10

−5

8 1.49 × 10

−5

15 6.98 × 10

−6

22 3.67 × 10

−6

Further Insights

There are a number of mathematical tools we can use to compute the best ﬁt of the

data to one of our reaction orders. One of these tools is the correlation coefﬁcient,

r, which tells how well any two measures are mathematically related to each other. A

perfect directly linear relationship would yield a correlation coefﬁcient, r,of1.As

infants grow, their height and weight give correlation coefﬁcients tending toward 1.

A perfect inverse relationship gives r values of −1. As we increase in age past about

45 years old, we inevitably run more slowly. Age and running speed in older runners

are inversely related and give an r value that is closer to −1. If there is no relation-

ship between variables, such as between human hair color and the number of straw-

berries people eat in July, we get an r value of 0. If a ﬁrst-order model were to ﬁt our

data, it would have the highest correlation coefﬁcient of the three possible models

that we have introduced.

PRACTICE 15.7

Plot the data for the following reaction as was done in Exercise 15.7. Determine the

overall order of this reaction.You may wish to use a graphing program to determine

which graph gives the straightest line.

2NO

(g) n 2NO(g) + O

(g)

646 Chapter 15 Chemical Kinetics

Time (s) [NO

] (M)

0 0.0100

50 0.0079

100 0.0065

150 0.0055

200 0.0048

300 0.0038

400 0.0031

See Problems 53, 54, 61, 62, 65, and 68.

15.5 Looking Back at Rate Laws

A summary of the data that we have discussed thus far is appropriate. In short,

here’s what we know so far:

■

Reaction rates determine the speed at which a reaction progresses but do not

reveal anything about the extent to which they produce a product.

■

We can measure the average rate if we know the initial and ﬁnal concentra-

tions over a particular time period.

■

The instantaneous rate is the rate at a given point in the reaction. It can be de-

termined by measuring the concentrations at points when the time difference

approaches zero, or it can be measured by determining the slope of a line

tangent to a plot of the rate versus time.

■

The initial rate is the instantaneous rate as the reaction starts.

■

The rate law is experimentally determined using the method of initial rates or

the method of graphical analysis.

+ +

HC C

CCH

Step 1

Step 2

CCH

Cytochrome P450

HC C

Methoxychlor

CCl

OCH

HC C

CCH

HC C

CCl

OCH

HC C

CCH

Cytochrome P450

HC C

bis-Hydroxy

methox

chlor

CCl

OCH

HC C

CCH

HC C

CCl

■

The half-life of a reaction is the time required for the concentration of a reac-

tion to reach 50% of the initial value.

■

Complex reaction orders can often be reduced to pseudo-ﬁrst-order reactions

by keeping the concentration of one of the reactants relatively large.

Speciﬁc information for the three rate orders that we have discussed is included

in Table 15.3. There are many more overall orders for reactions than those listed

here.

15.6 Reaction Mechanisms

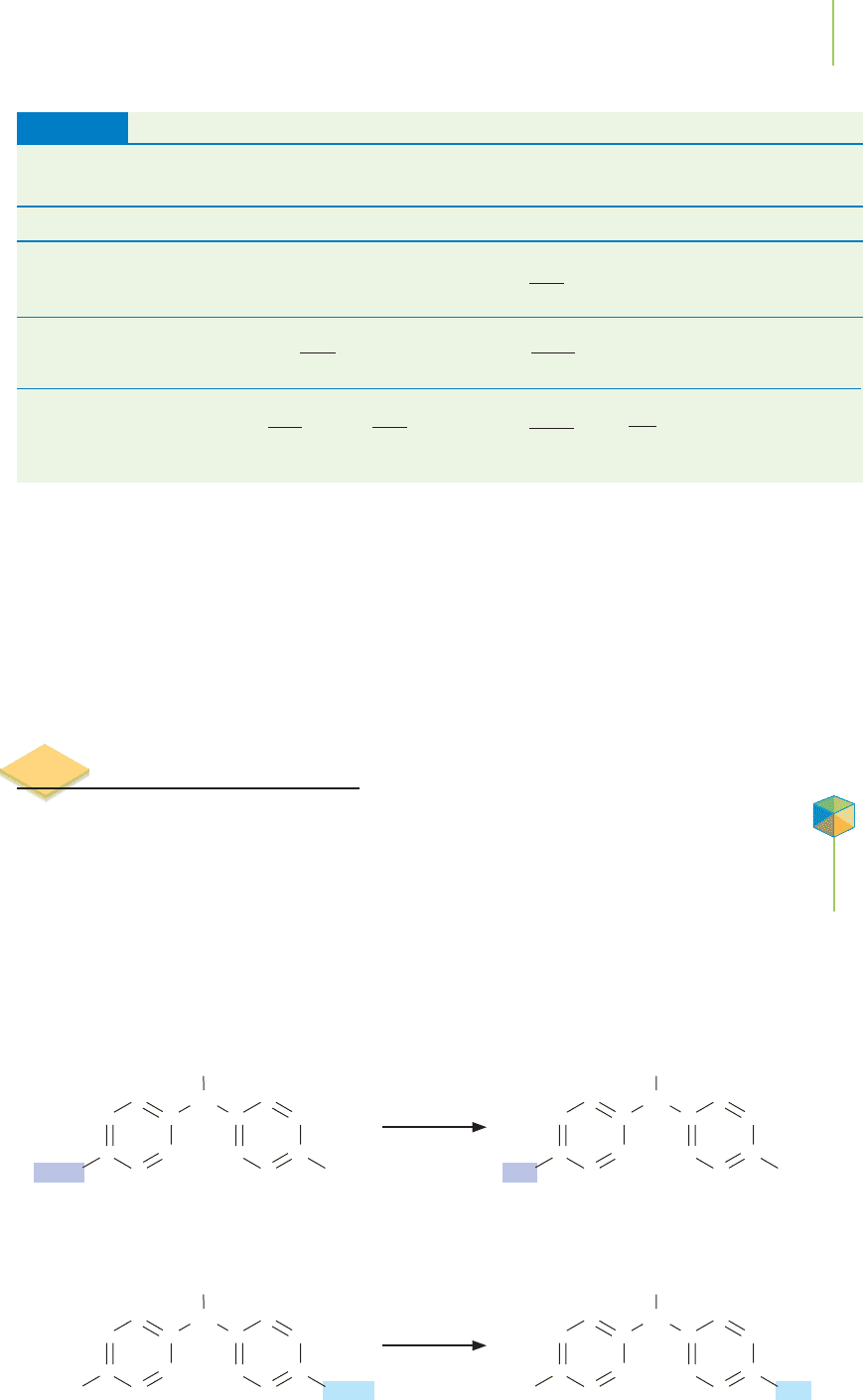
At this point, we need to do some detective work. In Exercise 15.2 we determined

the rate of metabolism of methoxychlor, an organochlorine insecticide, using ac-

tual values for the concentrations. However, upon deeper investigation, chemists

have found that the reaction proceeds in two sequential steps. In the ﬁrst step, the

methoxychlor undergoes reaction with water and cytochrome P450 (an enzyme

in the liver) to make mono-hydroxymethoxychlor. In a second step, the mono-

hydroxymethoxychlor reacts with another molecule of water and cytochrome

P450 and is converted into the product bis-hydroxymethoxychlor.

15.6 Reaction Mechanisms 647

Rate Laws

The value of the rate is reported in the units of concentration per unit time. The value of the rate constant

is different for each of the three orders (zero order = M/s; ﬁrst order =1/s; and second order =1/M·s).

Order Rate Law Integrated Rate Law Half-life Linear Plot

Zero Rate = k

[A]

=−kt +[A]

1/2

[

]

[A] versus t slope =−k

First Rate = k[A]



[A]



=−kt t

1/2

0.693

ln[A] versus t slope =−k

Second Rate = k[A]

[

]

= kt +

[

]

1/2

k[A]

[A]

versus

t slope =+k

TABLE 15.3

Application

HEMICAL

ENCOUNTERS:

Metabolism of

Methoxychlor