Kelter P., Mosher M., Scott A. Chemistry. The Practical Science

Подождите немного. Документ загружается.

Chemical

Equilibrium

Just as this balance settles at a ﬁxed

position of lowest energy, chemical

reactions “strive” toward a position of

lowest free energy—that is, chemical

equilibrium.

668

Contents and Selected Applications

16.1 The Concept of Chemical Equilibrium

Chemical Encounters: Myoglobin in the Muscles

16.2 Why Is Chemical Equilibrium a Useful Concept?

Chemical Encounters: Important Processes That Involve Equilibria

16.3 The Meaning of the Equilibrium Constant

Chemical Encounters: The Manufacture of Sulfuric Acid

16.4 Working with Equilibrium Constants

16.5 Solving Equilibrium Problems—A Different Way of Thinking

16.6 Le Châtelier’s Principle

Chemical Encounters: Catalysts in Industry

16.7 Free Energy and the Equilibrium Constant

Go to college.hmco.com/pic/kelterMEE for online learning resources.

669

“I’m running late.” We seem to hear

that expression so often in our hyper-

charged, have-to-do-it-now world. Running

late might mean being stuck in trafﬁc or on mass

transit. There is not much you can do in a sea of cars

and trucks. But sometimes you actually do run to get

where you are going. As you struggle to make up time, you

breathe more heavily than normal, desperately sucking air into your

lungs. Your body’s efforts to get more oxygen to the muscles are greatly

enhanced by a protein in muscle cells called myoglobin.

When you are resting, the myoglobin becomes loaded up with oxygen

molecules. These oxygen molecules can be quickly released when your

muscle cells undergo activity. How does the myoglobin acquire and re-

lease oxygen when we need it?

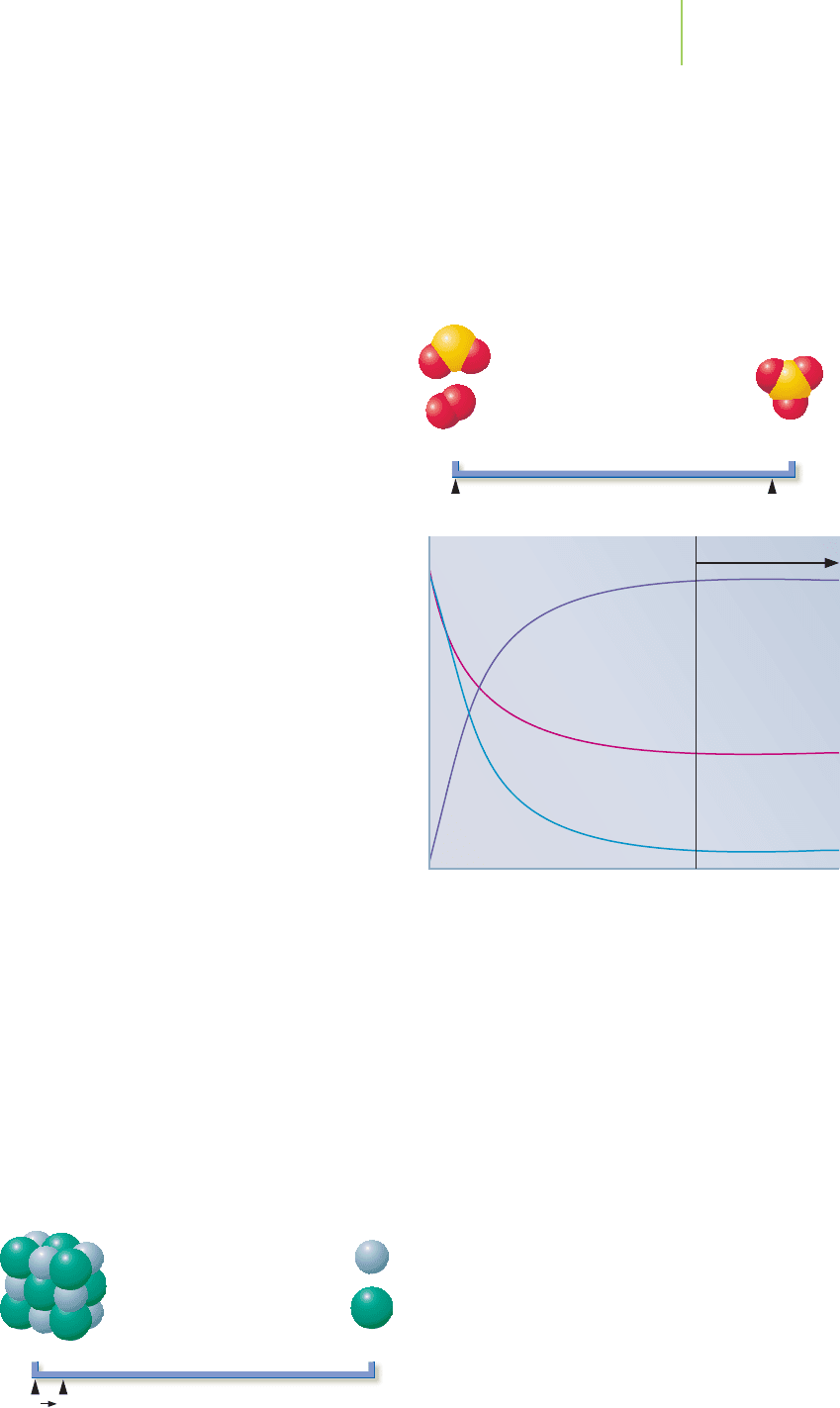
Myoglobin (Mb), shown in Figure 16.1, is a protein with a molecular

weight of about 16,900 g/mol. A key part of the protein is the

heme group,

shown in Figure 16.2. The heme contains an Fe

ion that can form a

bond with one molecule of oxygen,creating a myoglobin–oxygen complex

as follows:

Mb + O

n MbO

When your cells need the oxygen, it is released from the complex by reversing the

direction of the reaction:

MbO

n Mb + O

The free myoglobin is then available to bind more oxygen, which it can later release

as needed, and continue in this reversible cycle of bind–release–bind–release. Let’s

examine this reaction more closely to help us understand the concepts of reversible

reactions and the essential details of reactions such as this, which are known as

chemical equilibria.

Strenuous activities such as running

require a sharp change in the amount of

oxygen your muscles require. The inter-

action of myoglobin and oxygen in the

muscles accommodates this need.

Oxygen

FIGURE 16.1

Myoglobin (Mb) is a protein with a molecular weight of about

16,900 g/mol. A key part of the protein is the heme group,

highlighted on the left, which can bind to an oxygen molecule.

COOH

Fe NN

FIGURE 16.2

This drawing of a heme group highlights the Fe

ion, which

can bind to one molecule of oxygen as shown.

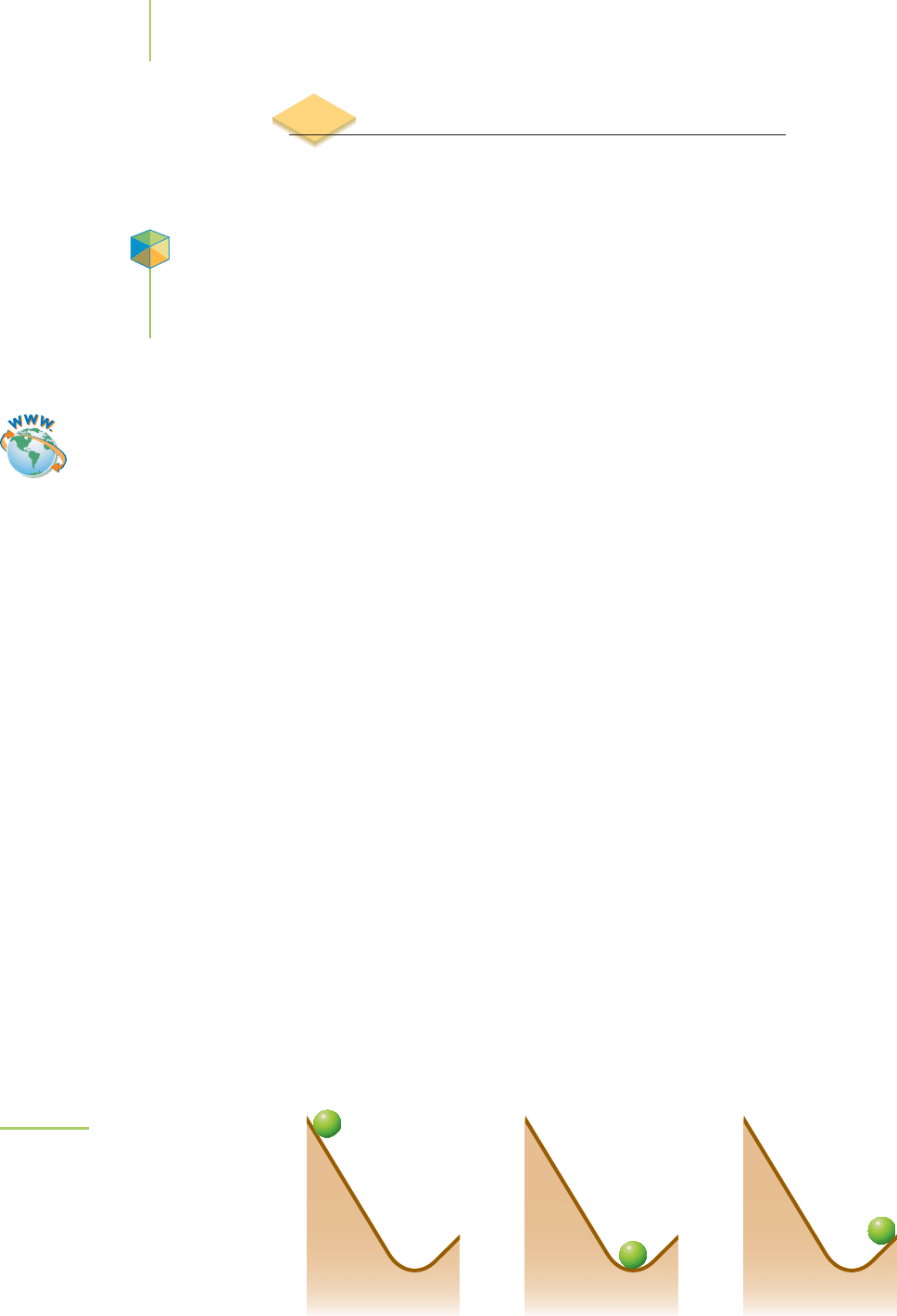
16.1 The Concept of Chemical Equilibrium

Why does myoglobin’s reversible cycle of binding and releasing oxygen take

place? We know from our understanding of thermodynamics (Chapter 14) that

spontaneous reactions lower the free energy, G, of the chemicals involved. When

we consider myoglobin and oxygen in living systems, we ﬁnd that the two com-

peting reactions exist. In one, myoglobin combines with oxygen. In the other, the

MbO

complex releases oxygen. The end result is that the molecules in each reac-

tion will never be completely converted into products, because these products are

always being converted back into reactants. In a closed system, these reversible re-

actions will settle into a state in which the forward and reverse reactions occur at

equal rates, where no net change in the concentrations occurs, even though both re-

actions continue. We describe this state as the position of chemical equilibrium,

or just

equilibrium (the plural is equilibria). What thermodynamic parameter

determines when an equilibrium exists? The concentrations will no longer change

when the free energy of the system is at a minimum for the process. At that point, the

change in free energy of the system, ∆G, is 0 kJ/mol.

We symbolize a system that can settle into equilibrium by using double ar-

rows, to represent the fact that both the forward and reverse reactions occur. For

example, the myoglobin and oxygen reaction equilibrium is written

Mb + O





MbO

As discussed in Chapter 15, we express the molar concentration of a substance by

placing its chemical symbol in brackets, [ ], such as [Mb] or [MbO

Let’s examine what happens to the concentrations of the reactants and prod-

ucts as the minimum free energy is approached (see Figure 16.3.) To make things

as straightforward as possible, we will consider the reaction occurring in a beaker,

rather than in the human body where all kinds of complications (such as “run-

ning late”) affect the chemistry.

Let’s assume that we place oxygen in our beaker so that its concentration is

3.0 ×10

−4

M.Wewouldsay[O

]

=3.0 ×10

−4

M,where the subscript0 means the

concentration at “time =0,” which is another way of saying the initial concentra-

tion. In fact, the amount of myoglobin normally present in muscle cells varies a

great deal among, and within, biological species. In humans, a mid-range value

is [Mb]

=2.0 ×10

−4

M. We will assume for this discussion that we have a closed

system (not the human body) and that there is no MbO

complex initially, so

[MbO

]

= 0 M. As the reaction proceeds, oxygen binds to myoglobin. The

forward reaction proceeds with a rate constant of k

,known in this particular reac-

tion as the

binding rate constant.

Mb + O

n MbO

670 Chapter 16 Chemical Equilibrium

Application

HEMICAL

ENCOUNTERS:

Myoglobin in

the Muscles

FIGURE 16.3

Like a ball ﬁnding its lowest energy point

in a valley, reactions ﬁnd their lowest free

energy position. This is the equilibrium

position (B).

Video Lesson: The Concept of

Equilibrium

Tutorial: The Equilibrium

Condition and Equilibrium

Constant

FIGURE 16.5

Equilibrium is a dynamic process. The

forward and reverse reactions are occur-

ring at equal rates. The result is no net

change in concentration of Mb (the blue

shapes), O

(the red dots), or MbO

equilibrium.

The concentration of oxygen decreases, as does that of free myoglobin,

as shown in Figure 16.4. The concentration of the MbO

complex in-

creases from zero as the reaction proceeds. As soon as the MbO

com-

plex forms, however, it begins to dissociate back into Mb and O

with

a rate constant of k

–1

, known in this particular reaction as the release

rate constant

–1

MbO

n Mb + O

Both reactions proceed until the free energy of the system is at a min-

imum, which occurs when the rates of the forward and reverse reactions

are equal. That statement embodies the two key ways to deﬁne chem-

ical equilibrium:

Deﬁnitions of Equilibrium

1. The free energy change of both forward and reverse reactions is

zero (∆G =0), and the free energy of the system is at its minimum.

2. The rates of the forward and reverse reactions are equal.

rate

= rate

[Mb][O

] = k

−1

[MbO

]

This is shown in Figure 16.5. The forward and reverse reactions that

bind and release oxygen are still occurring. In fact, they are occurring at the same

rate. Therefore, equilibrium is a dynamic process. And there is no overall change in

the concentration of Mb, O

, or MbO

at equilibrium.

16.1 The Concept of Chemical Equilibrium 671

Concentration

Time

[Mb]

]

[MbO

]

FIGURE 16.4

When myoglobin and oxygen are mixed, the con-

centration of oxygen decreases, as does that of

free myoglobin, as shown.The concentration of the

MbO

complex increases from 0 M. As soon as

the MbO

complex forms, however, it begins to

dissociate back into Mb and O

Time Time Time Time

Reactants Product

Equilibrium

The initial concentrations of reactants and

products change over time until equilibrium

is reached. At this point, the forward and

reverse reactions continue to produce their

respective products, but the overall concen-

trations of each component in the reaction

remain constant.

672 Chapter 16 Chemical Equilibrium

EXERCISE 16.1 Equilibrium Concentrations

Hydrogen and iodine gases can be combined to form hydrogen iodide,

(g) + I

(g) 



2HI(g)

Given the following initial and ﬁnal concentrations, calculate the equilibrium con-

centration of HI.

]

= 0.037 M [H

]

= 0.121 M [HI]

= 0.099 M

] = 0.022 M [H

] = 0.106 M [HI] = ??? M

First Thoughts

The mole ratios of reactants to product are 1-to-1-to-2, so 1 mol each of H

and I

react to produce 2 mol of HI in a constant volume. Because the volume remains

constant, we can think of the reaction stoichiometry this way: 1 M H

and 1 M I

react to produce 2 M HI.

Solution

The concentrations of I

and H

both decrease by 0.015 M.

0.015 M H

(or I

) ×

2M HI

1M H

(or I

)

= 0.030 M HI produced

[HI] = [HI]

+ 0.030 = 0.13 M

Further Insights

Much of the discussion in this chapter and in those that follow will consider how we

can predict equilibrium concentrations when we know only about the system and

the initial conditions. We will spend considerable time later in this chapter dis-

cussing how the ability to predict what will happen in a system is important in the

chemical industry. For example, in the development of a manufacturing process,

understanding how changes in conditions affect the equilibrium process enables

the manufacturer to produce the largest possible yield of product, as well as save the

company (and ultimately the consumer) money.

PRACTICE 16.1

Calculate the equilibrium concentration of HI if [I

]

= 0.050 M,[H

]

= 0.044 M,

[HI]

= 0.206 M, and [I

] = 0.041 M.

See Problem 21.

It has been shown by experiment that the equilibrium concentrations of myoglo-

bin, oxygen, and the MbO

complex are related by the ratio of the product to

reactant concentrations known as the

mass-action expression or, often, the

equilibrium expression, of the reaction.

K =

[MbO

]

[Mb][O

]

The value K is called the equilibrium constant for the reaction at a given tempera-

ture. We can get the equivalent result by separating the rate constants from the

concentrations in the rate expressions as follows. At equilibrium, the rate of

the forward and reverse reaction are equal.

[Mb][O

] = k

−1

[MbO

]

Rearranging the equation to put the rate constants on one side gives

−1

[MbO

]

[Mb][O

]

Video Lesson: The Law of Mass

Action and Types of Equilibrium

Therefore, the equilibrium constant, K, is the ratio of the forward rate constant to

the reverse rate constant.

K =

−1

The value for k

in the myoglobin–oxygen reaction at 20°C is 1.9 ×10

−1

·s

−1

and k

−1

is 22 M

−1

·s

−1

, so we can calculate the value of K:

K =

−1

1.9 ×10

= 8.6 ×10

We typically would express a calculation such as this by including the units.

However, the equilibrium constant does not have units. This is true because the

actual thermodynamic deﬁnition of an equilibrium constant is based on the ratio

of a substance’s concentration to a standard state concentration. Even though

the reasoning is subtle, the bottom line is that the equilibrium constant is typi-

cally given without units. In the reaction of myoglobin and oxygen, K is simply

8.6

These last two results—that there exists a mass-action expression to ﬁnd

the equilibrium concentrations of Mb, O

, and MbO

, and that there exists an

equilibrium constant for this expression at a particular temperature—can be

extended to any reversible reaction. For example, in a general equilibrium (reac-

tants A and B yielding products C and D) represented with stoichiometric coefﬁ-

cients m, n, p, and q,

mA + nB 



pC + qD

The mass-action expression is

K =

[C]

[D]

[A]

[B]

Exercise 16.2 explains why each equilibrium concentration is raised to the power

of its coefﬁcient in the mass-action expression.

EXERCISE 16.2 The Mass-Action Expression

The production of ammonia for use in fertilizers, via the Haber process, can be

depicted as

(g) + H

(g) + N

(g) 



(g) + NH

(g)

Write the mass-action expression for the formation of ammonia.

First Thoughts

We did something unusual by breaking the equation down to list each individual

molecule without the coefﬁcients, a rather cumbersome way of displaying an equa-

tion. Our goal in doing this is to demonstrate how the product of the coefﬁcients in

the mass-action is displayed in exponential form.

Solution

If we base the mass-action expression on the reaction exactly as it is written, we get

the following mass-action expression:

K =

[NH

][NH

]

][H

][N

]

[NH

]

Further Insights

The exponential form on the right-hand side is what we would have obtained had

we written the Haber process in the usual way:

(g) + N

(g) 



2NH

(g)

16.1 The Concept of Chemical Equilibrium 673

This shows why the mass-action expression includes the equilibrium concentration

of each substance raised to the power of its coefﬁcient. If the coefﬁcient is 1, as with

, it is not shown as an exponent, because raising anything to the power of 1 does

not change its value.

PRACTICE 16.2

One of the ways to produce hydrogen gas industrially involves the reaction of

methane with high-temperature steam. The reaction can be written as

(g) + H

O(g) 



CO(g) + H

(g) + H

(g)

Write the mass-action expression for this reaction.

See Problems 5 and 6.

EXERCISE 16.3 Practice with Mass-Action Expressions

Write the mass-action expression for each of these reactions:

a. PCl

(g) 



PCl

(g) + Cl

(g)

b. S

(g) 



8S(g)

c. Cl

(g) + 8H

(g) 



2HCl(g) + 7H

O(g)

Solution

In each case, the mass-action expression for the general reaction

mA + nB 



pC + qD

is of the form in which the equilibrium concentration of each reactant or product is

raised to the power of its coefﬁcient.

K =

[C]

[D]

[A]

[B]

Products Coefﬁcient of S

K =

[Cl

][PCl

]

[PCl

]

K =

[S]

]

Reactant

Coefﬁcient Coefﬁcient

of H

OofHCl

K =

[HCl]

[Cl

][H

]

Coefﬁcient of H

Note: Mathematically [C]

[D]

=[D]

[C]

, so the order in which we write these

terms doesn’t matter, as long as we keep each exponent with its term. For in-

stance, the exponent p must remain with [C].

PRACTICE 16.3

Write the equilibrium expression for each of these reactions:

a. NO(g) + O

(g) 



(g) + O

(g)

b. HCl(aq) + NH

(aq) 



Cl(aq)

c. C

(g) + 2H

(g) 



(g)

See Problems 9 and 10.

674 Chapter 16 Chemical Equilibrium

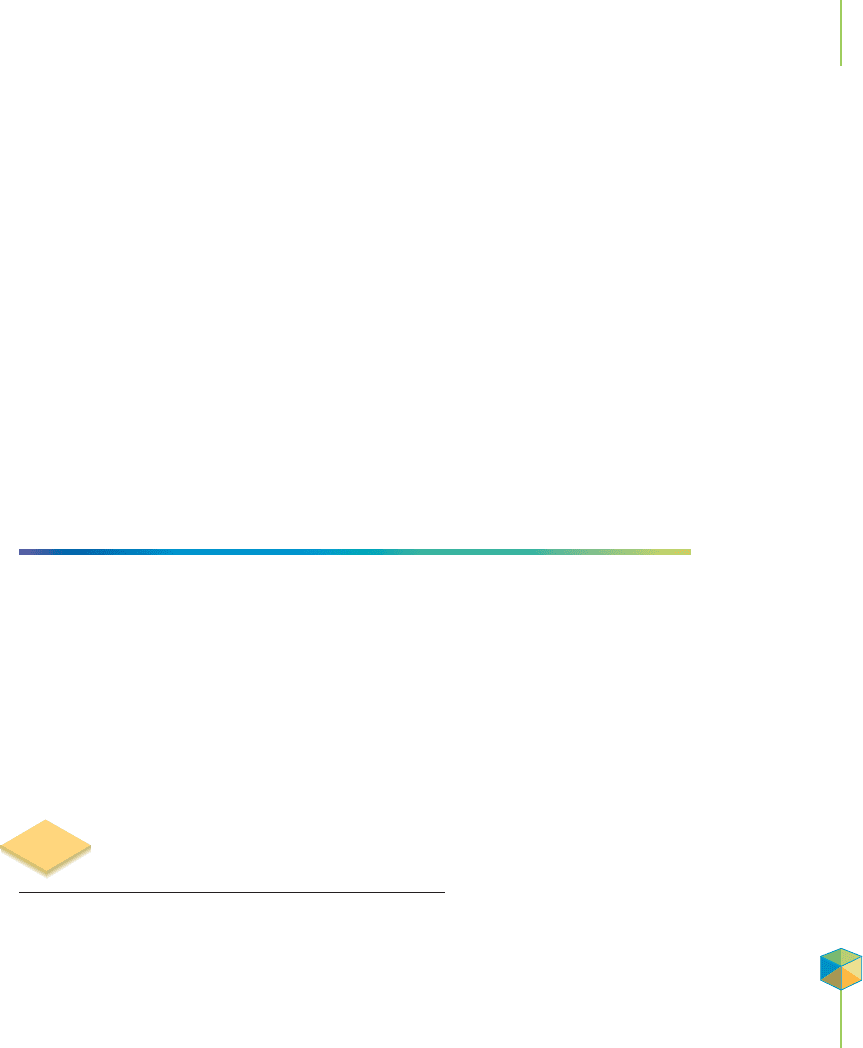
Concentration-based mass-action expressions are generally suitable repre-

sentations for the equilibria that occur in chemical reactions. However, in some

aqueous solutions, especially where the solute concentrations are high, chemists

often make a correction using activities instead of molarities, to get the most

meaningful results. For example, if we prepare a solution that contains 3.0 mol of

hydrochloric acid (HCl) in a liter of water, we say that the HCl concentration is

3.0 molar. We expect this strong acid to dissociate into H

and Cl

−

ions, and we

therefore assert that in the solution, the concentration of each ion, H

and Cl

−

,is

3.0 M. However, this is not completely true. Some of the hydrogen cations do in-

teract with the chloride anions in solution, and the ions interact with the water

solvent through ion–dipole interactions, as we discussed in Chapter 10. This

means that the effective concentration is likely to be somewhat different from the

intended concentration, especially in relatively concentrated solutions. This

effective concentration of the solute is called its

activity. We will generally not

consider the impact of activity in our discussions, but it is important for you to

know that such an idea exists and can be dealt with quantitatively.

HERE’S WHAT WE KNOW SO FAR

■

Most reactions do not go to completion. Rather, they reach a point of mini-

mum free energy. We call this the point the position of chemical equilibrium.

■

At chemical equilibrium, the rates of the forward and reverse reactions are

equal.

■

Chemical equilibrium is a dynamic, not static, condition.

■

A reaction at chemical equilibrium can be described by a mass-action

expression for which there is an equilibrium constant, K, that depends on

temperature.

16.2 Why Is Chemical Equilibrium

a Useful Concept?

The reaction of myoglobin with oxygen is just one of countless examples of

equilibrium processes in living systems. In fact, the chemistry of blood is ﬁlled

with equilibria. The chemistry of the environment also involves equilibrium

chemistry. As we will explore in Section 16.6, we can control the position of

equilibrium—that is, we can make it possible for reactions to proceed almost all

the way toward products or to reach a point at which mostly reactants exist. For

example, we can select the conditions so that the greatest possible amount of am-

monia is formed from hydrogen and nitrogen in the Haber process. We can also

maximize the amount of sulfur trioxide that is formed from the reaction of sul-

fur dioxide with oxygen as part of the industrial-scale preparation of sulfuric

acid. We can attempt to reduce the concentrations of acid in lakes and streams.

We can learn about the impact of chloroﬂuorocarbons (CFCs) on stratospheric

ozone levels. We can prepare pharmaceuticals to work in the most effective ways.

We can analyze for the presence of an extraordinary variety of substances, from

silver to steroids. We can do these things because we understand the fundamental

ideas of equilibrium. Our ability to use equilibrium concepts to control the extent

of chemical processes has the following vital implications:

1. Economic implications via the trillions of dollars of manufactured products

prepared and sold by the chemical industry.

2. Environmental implications for the quality of air, water, and land in the closed

system that is Earth.

3. Personal implications for our health.

16.2 Why Is Chemical Equilibrium a Useful Concept? 675

Application

HEMICAL ENCOUNTERS:

Important Processes

That Involve Equilibria

Application

HEMICAL

NCOUNTERS:

The Manufacture

of Sulfuric Acid

676 Chapter 16 Chemical Equilibrium

Table 16.1 lists some signiﬁcant processes that involve chemical equilibria.

Among them is chromatography, the subject of the accompanying boxed feature

on equilibrium and chromatographic analysis.

16.3 The Meaning of the Equilibrium Constant

More sulfuric acid (H

) is produced in the United States than any other

chemical; 37.5 billion kg were produced in 2004. Sulfuric acid has a wide range of

uses, the most important being the production of agricultural fertilizers. Its in-

dustrial and agricultural importance makes examining the manufacture of sulfu-

ric acid an excellent way to illustrate the meaning of the equilibrium constant.

Most of the sulfuric acid produced in the United States is made via the

Contact

process

, which began to be used on an industrial scale in 1880. The process is a set

of steps performed on readily available materials.

Step 1: The process begins with the sulfur provided by minerals such as iron

pyrite (FeS

) or hydrogen sulﬁde gas (H

S). The sulfur combines with oxygen

from the air.

S(s) + O

(g) 



(g)

Step 2: In this step, sulfur trioxide (SO

) is generated by the oxidation of SO

produced in step 1.

2SO

(g) + O

(g) 



2SO

(g)

Sulfur dioxide gas is passed over a catalyst bed containing 6–10% vanadium(V)

oxide (V

) at 600°C and then at 400°C. Temperature has a major effect on the

equilibrium of this reaction, as we will see.

Achievement of chemical equilib-

rium occurs in living systems,

chemical manufacturing, and the

environment. Equilibrium ﬁgures in

widely disparate processes related

to the chemistry of blood, ammonia

manufacture, steroid analysis, and

lakes and waterways.

Chemical Equilibrium Processes

Category Process Important Reaction

Industrial Contact process 2SO

(g) + O

(g) 



2SO

(g)

Industrial Haber process 3H

(g) + N

(g) 



2NH

(g)

Biological Myoglobin uptake of oxygen Mb(aq) + O

(aq) 



MbO

(aq)

Analytical Chromatographic analysis A

mobile phase





stationary phase

Analytical Metal analysis with EDTA Ca

+ EDTA

4−





CaEDTA

2−

Environmental Leaching of lead into water PbCO

(s) + 2H

(aq) 



(aq) +CO

(g) +H

O(l)

TABLE 16.1

Step 3: Sulfur trioxide (SO

) is then combined with concentrated sulfuric acid

and water to give more sulfuric acid in a net process that can be written as

(g) + H

O(l) 



(aq)

Let’s revisit step 2 of the contact process, the reaction of SO

and oxygen to

make SO

. The equilibrium constant, K, for this reaction at 27°C is 4.0 × 10

What does this value tell us about the relative amounts of reactants and products

when the reaction reaches equilibrium? When the value for K is very large, the

equilibrium lies essentially all the way to the products side.

(When we say,“reactants and products side,”we are always re-

ferring to these in terms of the forward reaction, written from

left to right.) The reaction goes almost, but not fully, to

completion. We can use a line chart, as shown to the right,

to visualize the meaning of the equilibrium constant for this

reaction by comparing the equilibrium position (E) to the

starting position (S). We start with only reactants (R) and

have no products (P). In practice, the contact process is not

carried out at 27°C because it takes too long for this reaction

to reach equilibrium at that temperature. In the chemical in-

dustry, time is money. To speed up the process, the tempera-

ture is raised, which lowers the equilibrium constant for this

reaction. Unfortunately, for this and many other equilibria,

the extent of the reaction indicated by the equilibrium constant

and the kinetics of the reaction (how fast it gets there), can force

us into a compromise between reaction speed and reaction yield.

We will discuss the interplay of these variables and their effect

on selecting reaction conditions in Section 16.6.

Every reaction has its own set of temperature-dependent

values of K (which is also known as K

when only concentra-

tions are used to determine its value), the equilibrium con-

stant. Our chapter-opening reaction of myoglobin with

oxygen has K = 8.6 × 10

at 20°C, which is fairly large. The

opposite, a small equilibrium constant, is also possible. For

example, an equation can be written that illustrates the for-

mation of silver and chloride ions in a saturated solution of silver chloride (AgCl)

from solid AgCl. Recall from Chapter 11 that a saturated solution is one in which

no more solute will dissolve. The small equilibrium constant of 1.7 ×10

−10

indi-

catesthatthe product concentrationsarequitesmall,[Ag

]=[Cl

−

]=1.3×10

−5

This implies that very little silver chloride dissolves at 25°C before equilibrium

(the saturated solution) is reached.

AgCl(s) 



(aq) + Cl

−

(aq) K = 1.7 × 10

−10

When the value for K is very small, the equilibrium lies nearly all the way to the

reactants side. We can show this using our line chart. In this case, the equilibrium

position is quite close to the silver chloride reactant, and we would say that silver

chloride isn’t very soluble in water.

16.3 The Meaning of the Equilibrium Constant 677

Reactants

Products

Concentration

Time

Equilibrium

[SO

]

[SO

]

As the reaction proceeds, the concentra-

tion of product increases and the con-

centrations of reactants decrease. At

some point, the concentrations of each

component reach and maintain a con-

stant value. This is the point when equi-

librium is reached.

Reactants

Products