Kelter P., Mosher M., Scott A. Chemistry. The Practical Science

Подождите немного. Документ загружается.

10.6 Applications of the Ideal Gas Equation

Atmospheric chemists not only know the relationships that dictate how gases be-

have but also understand the applications of these relationships as ways to solve

real-world problems. Many of their calculations—such as those that determine

how high a balloon will travel—can be done using the mathematical adjustments

of the van der Waals equation, but close approximations can be obtained using

the ideal gas equation. Other applications of this equation are equally useful.

They can be broken down into two main types: those that address physical prop-

erties and those that address chemical reactions. Examples of these applications

follow.

Physical Change Applications

The key questions to ask when applying the ideal gas equation are the same as in

any problem solving. “What do I want? How do I get there? What answer do I

expect? Does my answer make sense?” The following two exercises illustrate how

the ideal gas equation, density, and the molar mass of gases are related.

EXERCISE 10.12 An Application of Gas Density

The density of liquid nitrogen at −196°C is 0.808 g/mL. What volume of nitrogen

gas at STP must be liqueﬁed to make 20.0 L of liquid nitrogen?

First Thoughts

We can work backwards, via the density, to ﬁnd how many moles of liquid nitrogen

there are in 20.0 L of liquid nitrogen. This is the amount of gas that must be lique-

ﬁed. We can then use the ideal gas equation to convert from moles of N

to liters of

the gas.

Solution

g liquid N

= 20.0 L liquid N

1000 mL liquid N

1 L liquid N

0.808 g liquid N

1 mL liquid N

= 16,160 g N

1 mol N

28.0gN

= 577 mol N

PV = nRT

1.00 atm × V = 577 mol ×



0.08206 L·atm

mol·K



× 273 K

V = 1.29 ×10

Further Insights

Many gases, such as oxygen, ammonia, and nitrogen, are converted to liquids for

shipping and then used on-site as gases. As we see in this example, a lot of liquid ni-

trogen can be shipped in this way. Alternatively, as we learned previously, gases are

shipped under pressures approaching 150 atm in compressed gas tanks.

PRACTICE 10.12

A gas at 16°C and 1.75 atm has a density of 3.40 g/L. Determine the molar mass of

the gas. (Hint: Begin by assuming 1.00 L of the gas, and then determine the number

of moles that would occupy this volume.)

See Problems 47, 50, 53, 55, and 67.

418 Chapter 10 The Behavior and Applications of Gases

Dimensional analysis can lead us to a useful formula that we can use to determine

the molar mass of a gas, as was requested in Practice 10.12. The symbol M is the

variable used to represent molar mass, and it is also used to represent molarity.

We will underline the variable for molar mass (M

) to help distinguish between

the two. Translating the quantities back into the variables they represent, we ﬁnd

that the relationship between molar mass and density is

dR T

gg g

3.40 g L

−1

(0.08206 L·atm·mol

−1

·K

−1

) (289 K)

1.75 atm

M =

dRT

We see from this equation that the molar mass of an ideal gas is directly propor-

tional to its density. This relationship approximately holds for real gases that have

close to ideal behavior, but it does not hold for liquids or solids. As this equation

indicates, you can determine the molar mass of a gas if you can measure its

density.

Chemical Reactions—Automobile Air Bags

When a car crash occurs, the car stops suddenly. The occupant, however, contin-

ues to move with great velocity toward the steering wheel or dashboard. The de-

ployed air bag distributes over a large area (that of the air bag) the force that the

occupant would otherwise exert on the dashboard, minimizing the pressure on

any particular part of the occupant’s upper body. The result is an accident that

causes less bodily injury than an accident in which no air bag is deployed.

Inside the most common style of air bag is a capsule of sodium azide (NaN

iron(III) oxide (Fe

), and a small detonator cap that is rigged to start the

decomposition of NaN

2NaN

(s) n 2Na(s) + 3N

(g)

The nitrogen gas inﬂates the bag to its full volume (74 L for front air bags) within

50 ms of a crash. The sodium metal that is also generated in the reaction reacts

quickly with the iron(III) oxide to form sodium oxide. This second reaction is

necessary to remove dangerous sodium metal.

6Na(s) + Fe

(s) n 3Na

O(s) + 2Fe(s)

EXERCISE 10.13 Filling the Air Bag

A technician is designing an air bag for a new model car. She wants to use 72.0 g of

sodium azide (NaN

) to inﬂate the bag at 22.0

C and 1.00 atm. What is the maxi-

mum volume of the air bag under these conditions?

First Thoughts

The air bag reaction is notable not only because the bag is ﬁlled with nitrogen gas,

not air, but also because the stoichiometry of the reaction indicates that 3 mol of N

are formed from the decomposition of 2 mol of NaN

. This must be taken into

account in solving the problem.

10.6 Applications of the Ideal Gas Equation 419

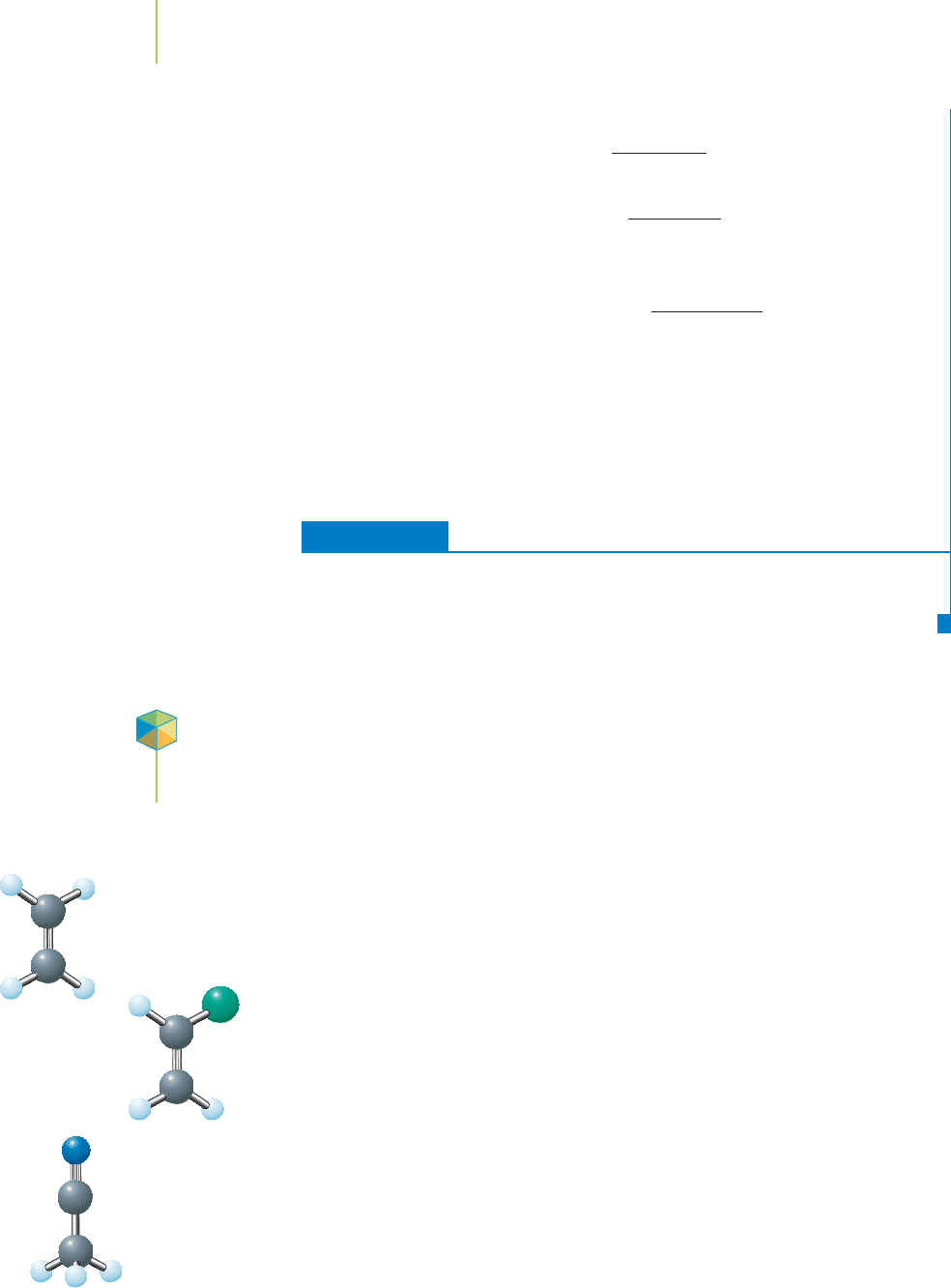
Application

HEMICAL

ENCOUNTERS:

Automobile

Air Bags

Air bags save lives by redistributing the

force of a person’s body over a larger area.

Azide ion

Solution

mol NaN

= 72.0 g NaN

1 mol NaN

65.0gNaN

= 1.108 mol NaN

mol N

= 1.108 mol NaN

3 mol N

2 mol NaN

= 1.662 mol N

PV = nRT

1.00 atm × V = 1.662 mol ×



0.08206 L·atm

K·mol



× 295 K

V = 40.2L

Further Insights

The amount of chemistry that occurs in 50 ms is startling, and the effects are pro-

found. Between 1987 and 2001, nearly 8400 lives in the United States alone were

saved by air bag deployments in motor vehicle accidents.

PRACTICE 10.13

How many grams of sodium azide would be required if the volume of the air bag

were to be 30.9 L at 31°C and 1.00 atm?

See Problems 59 and 60.

Chemical Reactions—Acetylene

Acetylene (C

) is an industrial gas used in welding and in the manufacture

of vinyl chloride (CH

CHCl), acetonitrile (CH

CN), and other industrial

chemicals, including polymers such as “neoprene.” The gas was ﬁrst prepared

inadvertently in the early 1890s by Thomas Willson, who owned a small alu-

minum-making company. In his quest to more effectively convert bauxite, com-

posed mostly of aluminum oxide (Al

) to aluminum metal, he combined the

ore with lime (CaO), and coal tar (mostly carbon compounds) in a furnace. A

gray solid was formed that, when reacted with water, gave off a ﬂammable gas.

After receiving a sample of the solid from Willson, Francis Venable of the Univer-

sity of North Carolina–Chapel Hill determined that Willson had made calcium

carbide (CaC

)

CaO(s) + 3C(s) n CaC

(s) + CO(g)

The calcium carbide reacted with water to form acetylene (C

) which had been

discovered by Edmund Davy in 1836.

CaC

(s) + 2H

O(l) n Ca(OH)

(s) + C

(g)

Acetylene has a great many industrial and commercial uses. Acetylene torches are

commonly used to weld and cut metals. The demand for acetylene is currently

met using a process different from that discovered by Willson and Davy. Acety-

lene can be made by pyrolysis (adding heat to convert organic solids into gases

and liquids) of methane, the main component of natural gas:

2CH

(g) n C

(g) + 3H

(g)

Acetylene burns with a much brighter ﬂame than many other fuels, leading to

the use of acetylene as a light source in many areas. Its use as a lamp by miners as

they work underground is most notable. Acetylene also burns very hot, at about

3000°C, when reacted with oxygen, giving rise to its use in welding and cutting

equipment.

420 Chapter 10 The Behavior and Applications of Gases

Application

HEMICAL

ENCOUNTERS:

Acetylene

Ethylene

Acetonitrile

Vinyl chloride

EXERCISE 10.14 Production of Acetylene

A small chemical company is setting up the facilities to produce acetylene. Planners

want to know what volume of C

will be produced from the reaction of

4.25 × 10

g of methane if the product is to be stored at 38°C and 1.00 atm. Assume

a yield of 34%.

First Thoughts

A good problem-solving strategy is to determine the amount of acetylene that can

be formed assuming a 100% theoretical yield, and then reduce it to account for the

34% actual yield. We can start by converting grams of methane to moles of methane

and then to moles of acetylene, remembering the 2-to-1 mole ratio of methane to

acetylene. We can use the ideal gas equation to ﬁnd the volume of C

assuming

100% yield and then, ﬁnally, adjust for the lower yield.

Solution

mol CH

= 4250 g CH

1 mol CH

16.0gCH

= 265.6 mol CH

mol C

= 265.6 mol CH

1 mol C

2 mol CH

= 132.8 mol C

PV = nRT

1.00 atm × V = 132.8 mol ×



0.08206 L·atm

mol·K



× 311 K

V = 3.39 ×10

The volume of 3.39 × 10

L assumes a 100% yield. Because the actual yield is 34%,

we must multiply 3.39 × 10

L by 0.34, to get the ﬁnal volume of 1.15 × 10

L of

Further Insights

We have discussed the preparation of several industrial gases. Some are shipped as

compressed gases, others as liquids. Using the Internet, you can gain additional food

for thought by ﬁnding out which ones are shipped in what way and why.

PRACTICE 10.14

How many grams of methane would be needed to produce 5.00 × 10

L of C

Again, assume that the actual yield of the reaction is only 34% under the same stor-

age conditions.

See Problems 65 and 66.

10.6 Applications of the Ideal Gas Equation 421

Miners use calcium carbide lamps

mounted on their helmets to see in

the dark recesses of a mine. Within the

lamp, water is slowly dripped onto a

piece of calcium carbide. The reaction

produces acetylene gas, which is

ignited in the center of a mirrored

reﬂector.

422 Chapter 10 The Behavior and Applications of Gases

HERE’S WHAT WE KNOW SO FAR

■

Avogadro’s, Boyle’s, and Charles’s laws can be combined into a equation that

relates the initial and ﬁnal states of a gas.

initial

ﬁnal

■

The ideal gas law provides information on the current state of a gas.

PV = nRT

■

The ideal gas constant (R) relates the value and the units needed to mathe-

matically operate the ideal gas law. R = 0.08206 L·atm·mol

−1

·K

−1

■

The molar mass of a gas can be determined using a modiﬁcation of the ideal

gas equation.

M =

dRT

10.7 Kinetic-Molecular Theory

The ideal gas laws are elegant in their simplicity and profound in their meaning.

Because of their simplicity, many scientists, including Bernoulli, Clausius,

Maxwell, Boltzmann, and van der Waals, sought to prove that the laws governing

the behavior of ideal gases were a result of the interactions among atoms and

molecules (collectively called “molecules” in the theory). The beauty of the re-

sulting

kinetic-molecular theory is that it enables us to arrive at the same conclusions

by thinking about the nature of molecules as we do from performing well-chosen

experiments. The experimental work and the theoretical work are consistent.

Both are based on the following statements that model gas behavior:

1. Gases are composed of particles. The particles are negligibly small compared

to their container and to the distance between each other.

2. Therefore, intermolecular attractions, which are exhibited at small distances,

are assumed to be nonexistent.

3. Gases are in constant, random motion, colliding with the walls of the container

and with each other.

4. Pressure is the force per unit area caused by the molecules colliding with the

walls of the container.

5. Because pressure is constant in a container over time, molecular collisions are

assumed to be perfectly elastic. That is, no energy of any kind is lost upon

collision.

6. The average kinetic energy of the molecules in a system is linearly propor-

tional to the absolute (Kelvin) temperature.

Using the Assumptions About Gas Behavior

to Rationalize the Gas Laws

Boyle’s Law (PV = constant)

Collisions with the walls of the container give rise to pressure. What would hap-

pen if the volume of the container were increased at a constant temperature for a

given number of molecules? Because temperature is a measure of the average ki-

netic energy of the molecules in the system, a constant temperature means that

the velocity of the molecules would stay the same. The same number of mole-

cules, traveling at the same speed, are bouncing off a larger total surface area, so

the pressure on a unit of surface area would fall.

Video Lesson: The Kinetic-

Molecular Theory of Gases

Visualization: Kinetic-Molecular

Theory/Heat Transfer

Visualization: Visualizing

Molecular Motion: Single

Molecule

Visualization: Visualizing

Molecular Motion: Many

Molecules

Charles’s Law (V/T = constant)

In this case, both the pressure and the number of molecules are constant. If the

volume is lowered, how can the number of collisions per unit time (a measure of

pressure) stay the same? The only way this can happen is if the velocity of the

molecules becomes slower, via lowering of the temperature. As a result, the more

slowly traveling molecules, which also have less kinetic energy, hit the now-closer

walls at the same rate as the more rapidly moving molecules did when the walls

were farther out.

Avogadro’s Law (V/n = constant)

How is it possible to keep the pressure and the average kinetic energy (tempera-

ture) of the molecules constant if the volume is increased? We need to add more

molecules to the system—that is, increase n—so that the number of collisions per

unit time in the larger system remains the same.

EXERCISE 10.15 The Importance of Assumptions

According to point 1 of the kinetic-molecular theory, “Gases are composed of mol-

ecules that are negligibly small compared to their container and to the distance be-

tween molecules.” Strictly speaking, this statement is not true for real gases. How

would the gas laws change if point 1 were not included?

Solution

One answer is that if the more realistic picture of gases were taken into account,

then the volume would depend on the nature of the gas. Gases composed of larger

atoms and molecules take up more volume and would therefore cause more devia-

tion from Boyle’s law. The b term in the van der Waals model for nonideal gas

behavior is one attempt to quantitatively account for this deviation.

PRACTICE 10.15

Explain, using the equations for kinetic energy, why two different molecules must

differ in speed if the molecules have identical kinetic energy. If their kinetic energies

are the same, which would be moving faster, a low-molecular-mass molecule or a

high-molecular-mass molecule?

See Problems 73–76.

A Closer Look at Molecular Speeds

The kinetic energy of a molecule is equal to

⁄2 mv

, in which m is the mass and v

is the velocity of that molecule. For a system with one type of molecule (that is,

m is constant), the temperature is proportional to the square of the velocity, v

Molecules move faster at higher temperatures, slower at lower ones.

For a gas containing Avogadro’s number of molecules, there are several addi-

tional ideas we must introduce. First, the term velocity means the rate of travel—

the speed—in a speciﬁed direction. If we have Avogadro’s number of molecules,

they will be traveling in all different directions, and the net velocity (including the

direction!) may well be zero meters per second, even if the individual molecules

are moving very rapidly. When we talk about the rate of travel of large numbers of

molecules, we are interested in their speed (how fast), not their velocity (how fast and

in what direction). Also, the collisions will not be perfectly elastic, and some en-

ergy will, in fact, be transferred. There will be a distribution of kinetic energies

among the many molecules and, therefore, a range of speeds that can be deter-

mined. Just as the SAT or ACT scores for students throughout the United States

have a fairly wide range, the speeds of individual molecules in a sample also have

10.7 Kinetic-Molecular Theory 423

Video Lesson: Molecular Speeds

a range of values. Just as there is an average SAT or ACT score, we can deﬁne the

average speed of i molecules as we would any average value; it is the sum of

the speeds divided by the number of molecules:

Speed

average

= (speed

+ speed

+···+speed

)/i

A related value, often used in discussions about the statistics of molecular behav-

ior, is the

root-mean-square (rms) speed, u. This is the speed that a molecule with

the average kinetic energy will have, and it is equal to the square root of the sum

of the squares of the individual speeds divided by the number of molecules—

that is,

u =





speed

+ speed

+···+speed





1/2

The average score on the SAT or ACT is not necessarily the most probable; it is

just the average. So it is with gases, for which there exists the

most probable speed,

α, of a gas. The root-mean-square speed, the average speed, and the most proba-

ble speed are related as 1.22 : 1.12 : 1.00.

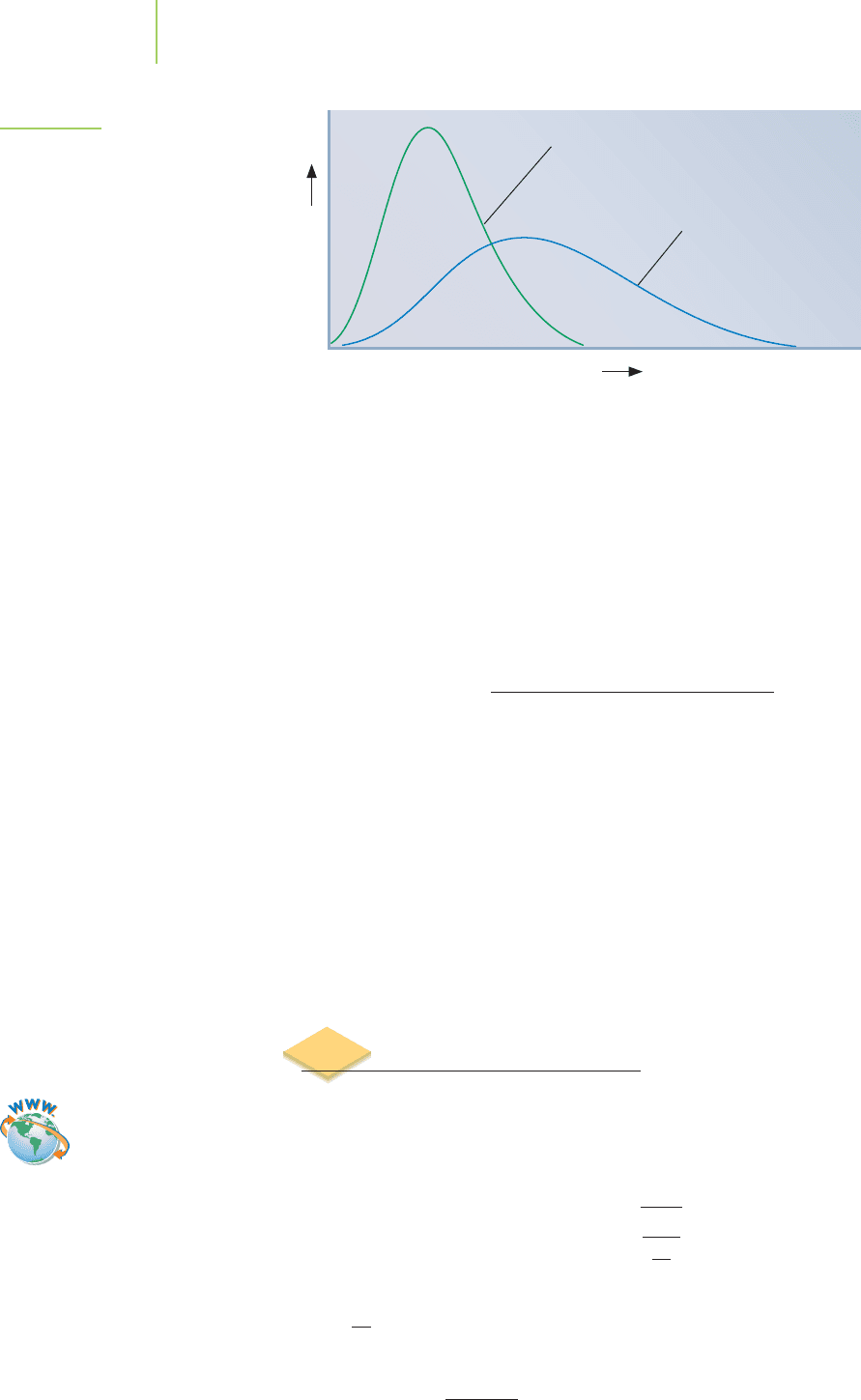
The distribution of molecular speeds at different temperatures for helium

and that for methane are shown in Figure 10.21. Why do methane molecules

move more slowly, on average, than those of helium at the same temperature?

Again we revisit the factors that account for kinetic energy (

⁄2 mv

). If two gases

are at the same temperature, their average kinetic energies will also be equal.

Methane (16.0 g/mol) is heavier than helium (4.00 g/mol), so its molecules must

be moving more slowly.

10.8 Effusion and Diffusion

At a given temperature (constant molecular kinetic energy =

⁄2 mv

), heavier gas

molecules move more slowly than their lighter counterparts. Although the math-

ematical derivation is fairly involved, it is possible, using the ideas of the kinetic-

molecular theory, to state that for any sample of gas, the rms speed is related to

the molar mass of the gas as follows:

rms



3RT

where T = the temperature in K

= the molar mass of the gas in kg·mol

−1

R = the ideal gas constant, 8.314 J·K

−1

·mol

−1

= 8.314 kg·m

·s

−2

·mol

−1

·K

−1



424 Chapter 10 The Behavior and Applications of Gases

Speed

Probability

He at 400 K or CH

at 1600 K

He at 100 K or CH

at 400 K

FIGURE 10.21

Molecular speeds are related to the

mass of the gas and to the temperature,

as shown here for helium and methane.

Why do methane molecules move more

slowly, on average, than those of helium

at the same temperature?

Video Lesson: Effusion and

Diffusion

Tutorial: Effusion and Diffusion

of Gases

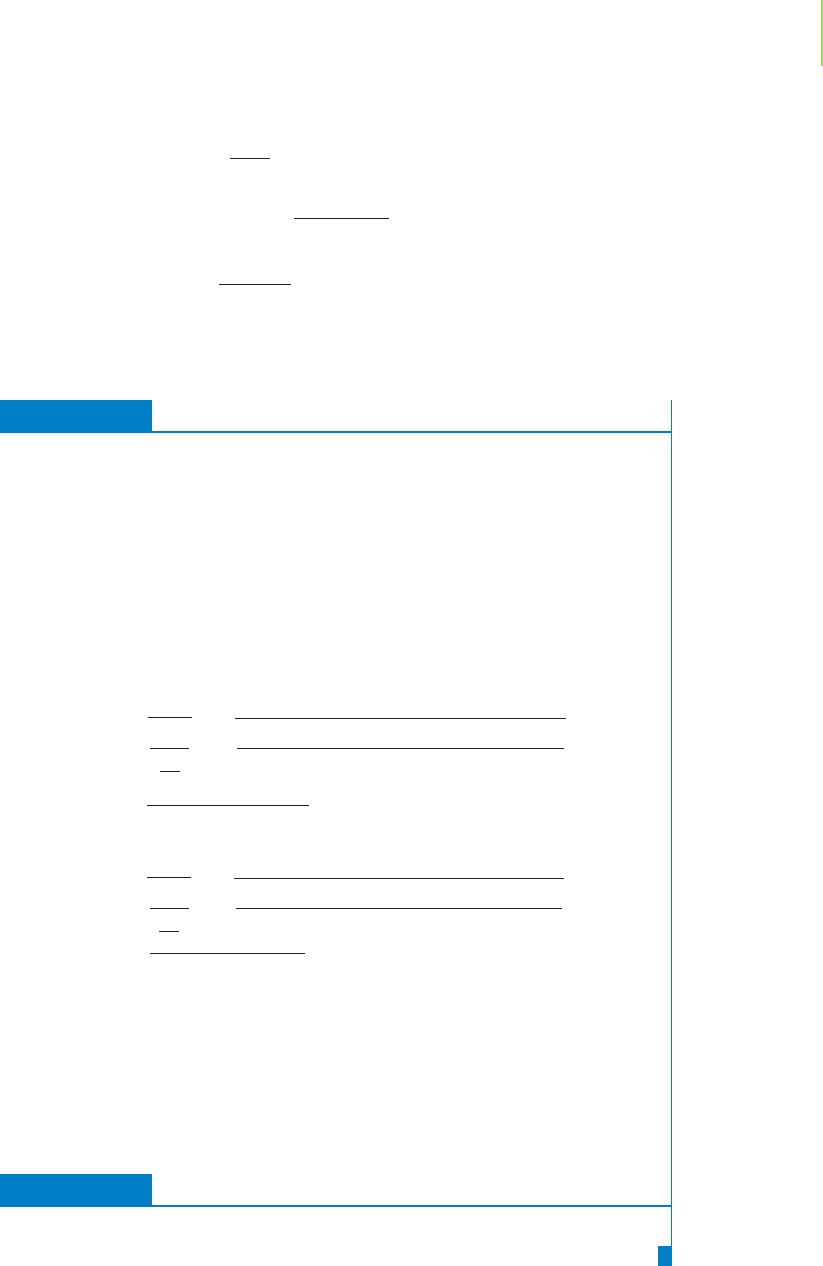
because

P × V =



force

area

× V





mass ×

acceleration

area

× volume



kg·m·s

−2

× m

= kg·m

·s

−2

EXERCISE 10.16 The rms Speed of Gases

Compare the rms speeds of methane and helium at 25

◦

First Thoughts

What do we expect and why? If you wanted to use an analogy when teaching a class

about the relationship between molar mass and speed, what might it be? A useful

analogy might be to compare the running speed of a 125-lb world-class marathon

runner to that of a 600-pound sumo wrestler, where the helium is the marathon

runner and the methane is the sumo wrestler.

Solution

For methane,

rms



3RT



3 ×8.314 kg·m

·s

−2

·mol

−1

·K

−1

× 298 K

0.0160 kg·mol

−1



4.645 × 10

·s

−2

= 682 m/s

For helium,

rms



3RT



3 ×8.314 kg·m

·s

−2

·mol

−1

·K

−1

× 298 K

0.00400 kg·mol

−1



1.858 ×10

·s

−2

= 1360 m/s

Further Insights

Note that the rms speed of methane is half that of helium, and that methane has a

molar mass four times the atomic mass of helium. This suggests that the speed of

gas molecules is inversely proportional to the square root of the molar mass. Note as

well the incredibly high speeds of these molecules!

PRACTICE 10.16

Which gas has a higher average speed at 20°C, F

or CO

See Problems 75–85.

In 1829, Thomas Graham (1805–1869) made measurements of the relative

rates at which gases pass through small openings into a very low-pressure re-

gion, a process called

effusion (Figure 10.22). His results, like those that led to the

other gas laws, predated the kinetic-molecular theory and conﬁrm our conclu-

sion regarding the relative speeds of gas particles. His measurements led to what

10.8 Effusion and Diffusion 425

= Nitrogen

= Oxygen

= Helium

we now know as Graham’s law of effusion. We can state this law mathematically.

For two gases of differing molar mass, M

and M

, the ratio of their effusion rates

(re

/re

) is equal to the square root of the inverse ratio of their molar masses

(



Effusion can be used to separate mixtures of gases that would be difﬁcult to

separate by other methods. Effusion has been used to separate

235

U and

238

U from

the natural mixture of uranium isotopes (0.72%

235

U and 99.28%

238

U). The sep-

aration of these two naturally occurring uranium isotopes from the uranium ore

called pitchblende (UO

) makes possible the construction of atomic fuel rods for

use in nuclear power plants as well the production of atomic weapons. The fun-

damental process requires converting the ore into solid uranium hexaﬂuoride

(UF

). At the processing facility, the solid is heated, and the UF

gas, containing

the

235

U and

238

U isotopes, is fed into a series of vessels. At each stage, the lower-

molar-mass UF

strikes the walls of the vessel more frequently than does the high

molar mass UF

. The vessel has semipermeable walls, so more of the lighter,

235

U-

containing UF

can ﬂow through. Hundreds of stages later, the resulting

“enriched”mixture contains about 5%

235

U. The mixture is then solidiﬁed for use

in nuclear power plants. Nuclear weapons require an enrichment to at least

90%

235

A related phenomenon is called

diffusion, which involves the mixing of one

gas with another or with itself. On a molecular level diffusion is far more com-

plex, because in mixing, molecules collide with each other after moving only a

very short distance—typically 5 × 10

−8

m, only hundreds of times the diameter

of a gas molecule itself. Therefore, mixing is a chaotic, rather slow process of the

dilution of two or more gases.

The food industry has a particular interest in the ability of gases to pass

through small openings, such as the pores of plastic wrap that surround meats

and other food items. The ability of oxygen to pass through these pores to the

food lowers its shelf life unless the packaging can maintain an inert atmosphere,

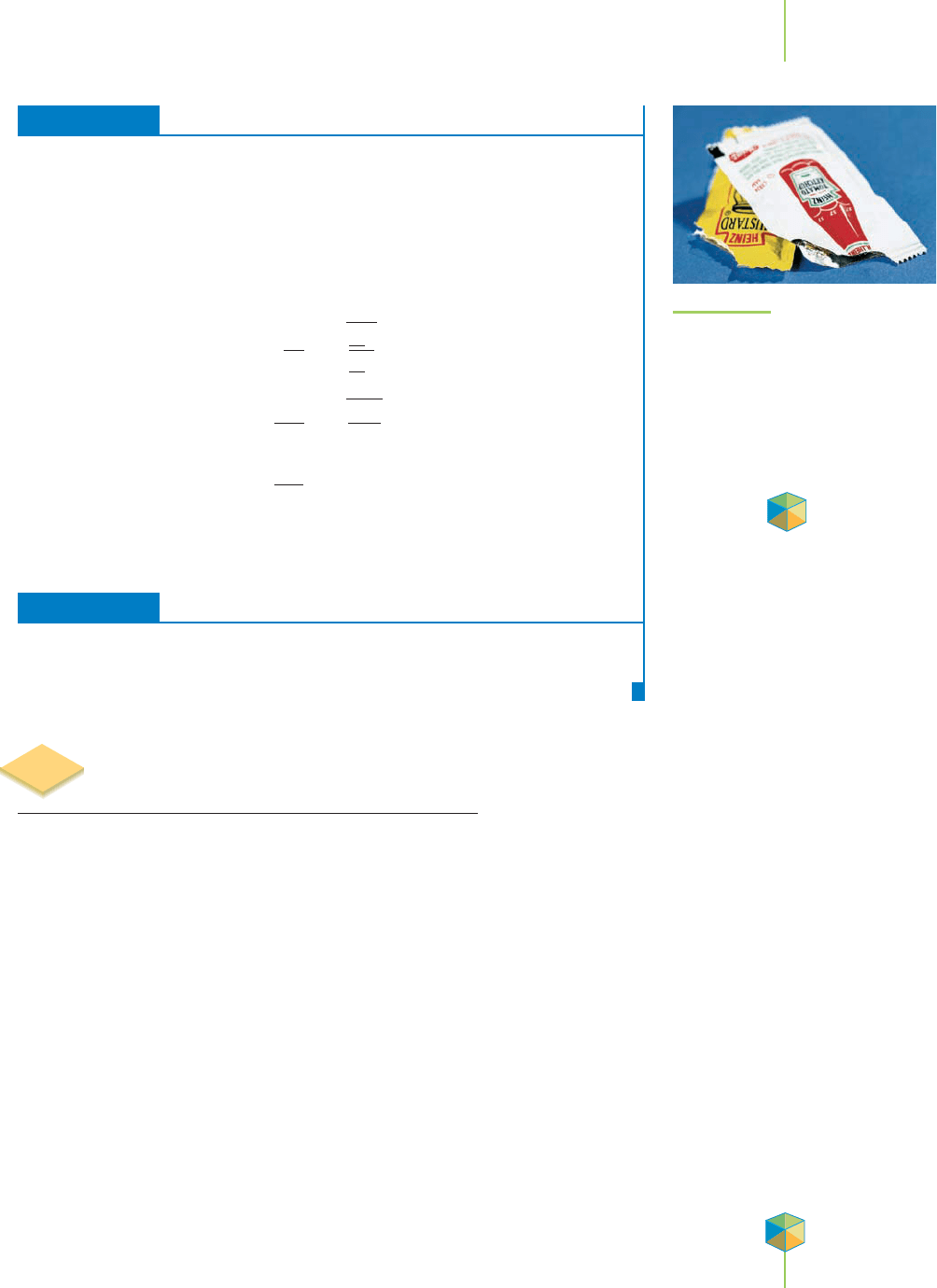
as discussed in Section 10.3. Small condiment packages of ketchup and mustard,

such as those in Figure 10.23, are usually packaged in several layers that include

plastic and foil. The foil helps prevent the exchange of air with the food, and the

plastic keeps the metals in the foil away from the food, with which they might

otherwise react.

426 Chapter 10 The Behavior and Applications of Gases

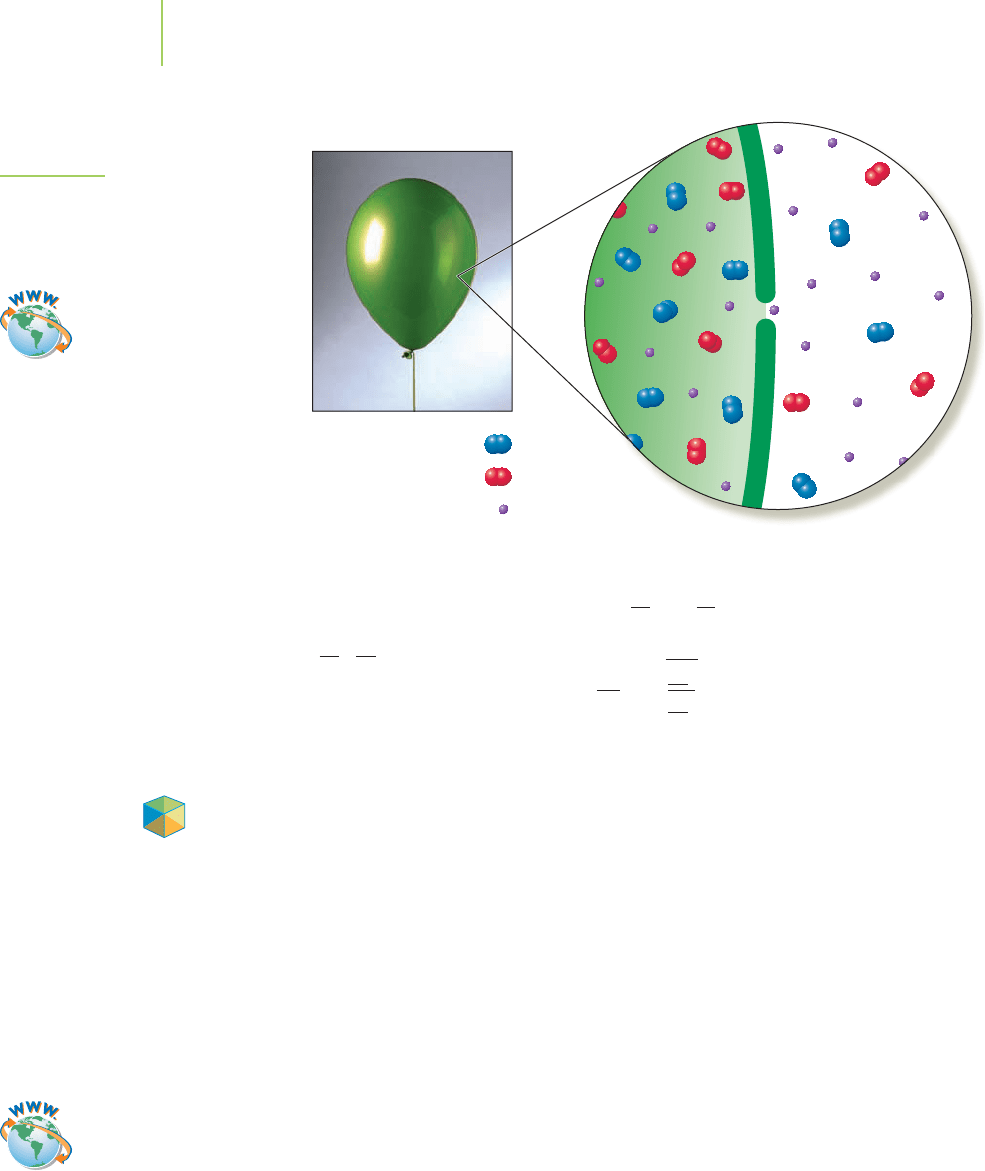
FIGURE 10.22

Gases effuse through a small opening in

their container. The faster molecules

escape through the opening more

rapidly than the slower molecules.

Application

Visualization: Effusion of a Gas

Visualization: Diffusion of Gases

Visualization: Gaseous

Ammonia and Hydrochloric Acid

EXERCISE 10.17 Effusion

A latex balloon ﬁlled with a mixture of N

and He is observed. Which gas would ef-

fuse through the pores in the latex balloon more rapidly? How much more rapidly

would it effuse?

Solution

The gas with the lower molecular mass, He, would effuse more rapidly. The ratio

can be calculated with Graham’s law of effusion:





28.0

4.00

= 2.65

Therefore, the helium gas would effuse from the balloon 2.65 times faster than the

nitrogen gas.

PRACTICE 10.17

Which effuses more rapidly under identical conditions, He or H

? How much more

rapidly?

See Problems 87, 88, 97, and 98.

10.9 Industrialization:

A Wonderful, Yet Cautionary, Tale

The glory of science and technology is our ability to modify nature’s bounty in

ways that enable us to sustain a world of nearly 7 billion people. As consumers, we

often ignore the impact that gases have on us. However, the chemical changes that

inhaled oxygen makes possible in our bodies sustain life. The chemical change of

combustion moves motorized vehicles of all shapes and sizes along our highways,

on our waterways, and on a ﬂuid bed of air in the sky. Gases can wreak havoc in

the form of tornadoes, hurricanes, and natural gas explosions, or lend calm to a

cool evening. They can kill when used as “nerve agents” in warfare or help heal

when used as anesthetics in surgery. As we modify nature, we recognize the

changes in the atmosphere that our 150-year-long focus on industrialization has

produced. These changes bear watching, for in the relative blink of an eye on the

global time scale, we risk unraveling the protective blanket that has taken nature

2 billion years to create. Two of the greatest concerns are changes in ozone con-

centration and the greenhouse effect.

Ozone

This pale blue gas, O

, is an allotrope of oxygen and is found in two of the four

layers of the atmosphere, the stratosphere and the surface layer called the tropo-

sphere. These layers and the important gases within them are shown in Fig-

ure 10.24. In the stratosphere, ozone absorbs much of the UV radiation that

would otherwise be harmful to us. UV radiation is typically categorized into

three regions based on the energy of the corresponding wavelengths. The UV-A

10.9 Industrialization: A Wonderful, Yet Cautionary, Tale 427

Application

FIGURE 10.23

Small condiment packages of ketchup

and mustard are usually packaged in

several layers that include plastic and

foil. The foil helps prevent the exchange

of air with the food, and the plastic

keeps the metals in the foil away from

the food, with which they might other-

wise react.

Application

HEMICAL ENCOUNTERS:

Ozone