Kelter P., Mosher M., Scott A. Chemistry. The Practical Science
Подождите немного. Документ загружается.

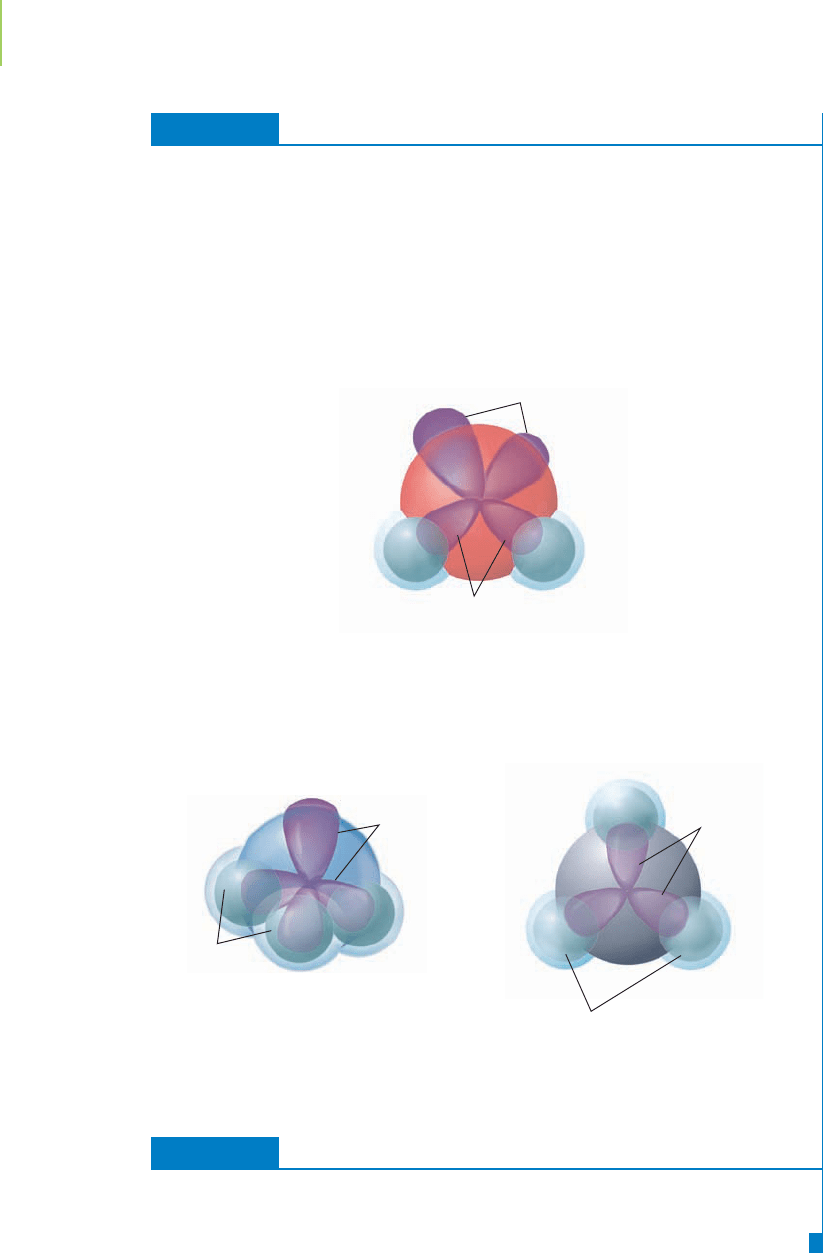
2sp
2
1s
AlH
3
2sp
3
1s
NH
3
2sp
3
1s
1s
2sp
3
H
2
O
c. AlH
3
geometry: The aluminum atom is sp
2
hybridized and has a trigonal
planar geometry. The bond angle is 120°.
PRACTICE 9.4
For each of the molecules in Practice 9.3, indicate the geometry about the central
atom.
See Problems 25–28, 35, and 36.
sp
3
d and sp
3
d
2
Orbitals
Hybrid orbitals can also be constructed to account for expanded octets.A good ex-
ample is phosphorus pentachloride (PCl
5
), a reactive molecule used to make com-
pounds containing chlorine. The Lewis dot structure model of PCl
5
indicates that
there should be five bonds to the phosphorus atom. Because the combination of
all of the s and p orbitals will allow only four bonds, we must include a d orbital
in the hybridization scheme. Five orbitals on the phosphorus can be made by
EXERCISE 9.4 Shapes of the Molecules
For each of the molecules in Exercise 9.3, indicate the geometry around the central
atom.
Solution
a. H
2
O geometry: sp
3
hybridized atoms adopt a tetrahedral geometry. Because
two of the sp
3
orbitals contain lone pairs, the VSEPR model indicates that the
molecule has an overall bent geometry. The bond angle should be less than
109.5° because the lone pairs repel each other more than the bonding pairs.
The angle HOOOH is actually 104.5°.
368 Chapter 9 Advanced Models of Bonding
b. NH
3
geometry: Again, we should have sp
3
hybridized orbitals with a tetrahe-
dral geometry. Because one of the sp
3
orbitals contains a lone pair, ammonia
has a trigonal pyramidal geometry. The bond angle (HONOH) should be
less than 109.5° because of the repulsions between the lone pair and the
bonding pairs of electrons (the angle is actually 107°).
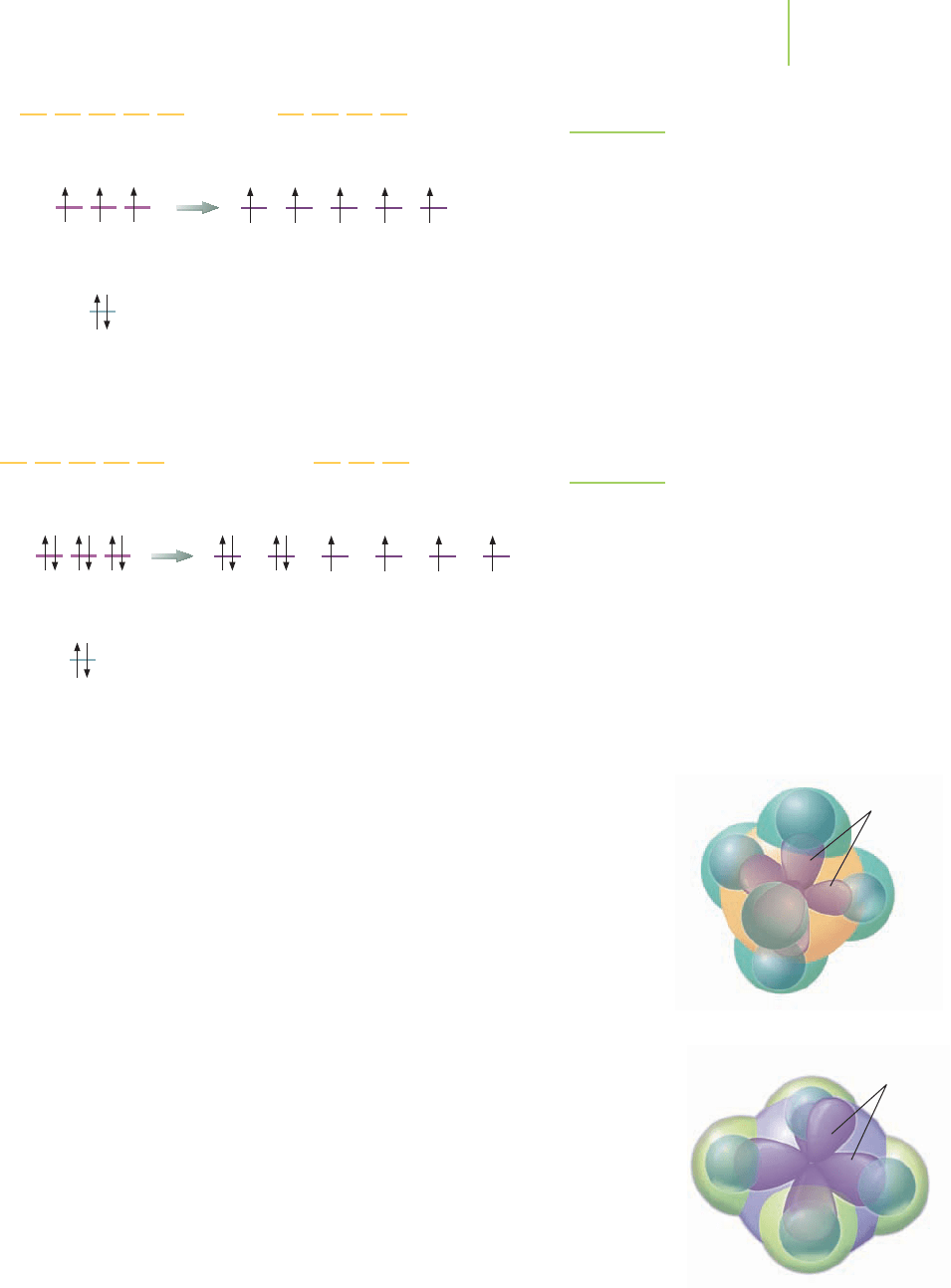
9.2 Hybridization 369
hybridizing the 3s, three 3p, and one of the 3d orbitals. The result is five degener-
ate 3sp
3
d orbitals. We can mix the d orbital because it is in the same principal en-
ergy level and is similar in energy to the other orbitals. The resulting valence bond
model of PCl
5
shows overlap of a 3p orbital from the chlorine atom with one of the
3sp
3
dorbitals from the phosphorus atom (Figure 9.15). The space-filling model of
the molecule shows how the orbitals fit together to give the molecule its essential
structure.
Other examples of expanded octets are found in compounds containing
xenon. The first example of a compound containing xenon, a noble gas, was made
in 1962. Shortly after the discovery that xenon could make compounds with other
elements, XeF
2
,XeF
4
, and XeF
6
were prepared. The orbital overlap required to
make xenon tetrafluoride (XeF
4
) shows why these compounds are possible. The
Lewis dot structure of XeF
4
requires six orbitals (four for bonds and two for
lone pairs). We hybridize a 5s, three 5p, and two 5d orbitals to make six degener-
ate 5sp
3
d
2
orbitals. Each bond in XeF
4
results from overlap of a 2p orbital from the
fluorine atom with a 5sp
3
d
2
orbital from the xenon atom, with the two lone pairs
on the xenon atom occupying two 5sp
3
d
2
orbitals (Figure 9.16).
Sigma and Pi Bonds
Our discussion so far has centered on the use of valence bond theory to address
the formation of single bonds in molecules. However, we know from Chapter 8
that atoms can participate in multiple bonds.
How is this possible if hybridization
provides only orbitals that are oriented directly at the atom with which they are
bonded?
The answer lies in the different ways in which orbitals can overlap in va-
lence bond theory.
Sigma bonds (σ bonds), which make up the framework of a
molecule, result from an end-on overlap of orbitals. Almost every “single bond”
is a sigma bond. In fact, every bond we’ve discussed thus far in this chapter results
from end-on overlaps of orbitals, such as the four σ bonds in CH
4
, each of which
3sp
3
d
5sp
3
d
2
Valence shell electron
configuration of phosphorus
Hybridized valence
shell on phosphorus
3d 3d 3d 3d 3d 3d 3d 3d 3d
3s
3p3p 3p
3sp
3
d 3sp
3
d 3sp
3
d 3sp
3
d 3sp
3
d
FIGURE 9.15
Hybridization of the phosphorus in PCl
5
. Because
five bonds are needed to complete the structure,
five orbitals are hybridized on the phosphorus atom
to give five new hybrid orbitals.
Valence shell electron
configuration of xenon
Hybridized valence
shell on xenon
5d 5d 5d 5d 5d 5d 5d 5d
5s
5p
5p 5p
5sp
3
d
2
5sp
3
d
2
5sp
3
d
2
5sp
3
d
2
5sp
3
d
2
5sp
3
d
2
FIGURE 9.16
Hybridization of xenon in XeF
4
.
Valence shell electron
configuration of carbon
Hybridization
of carbon
Four bonds can be formed
with these orbitals.
C
H
H
H
H
2p
2s
2p 2p
2sp
3
2sp
3
2sp
3
2sp
3
σ bond
σ bond
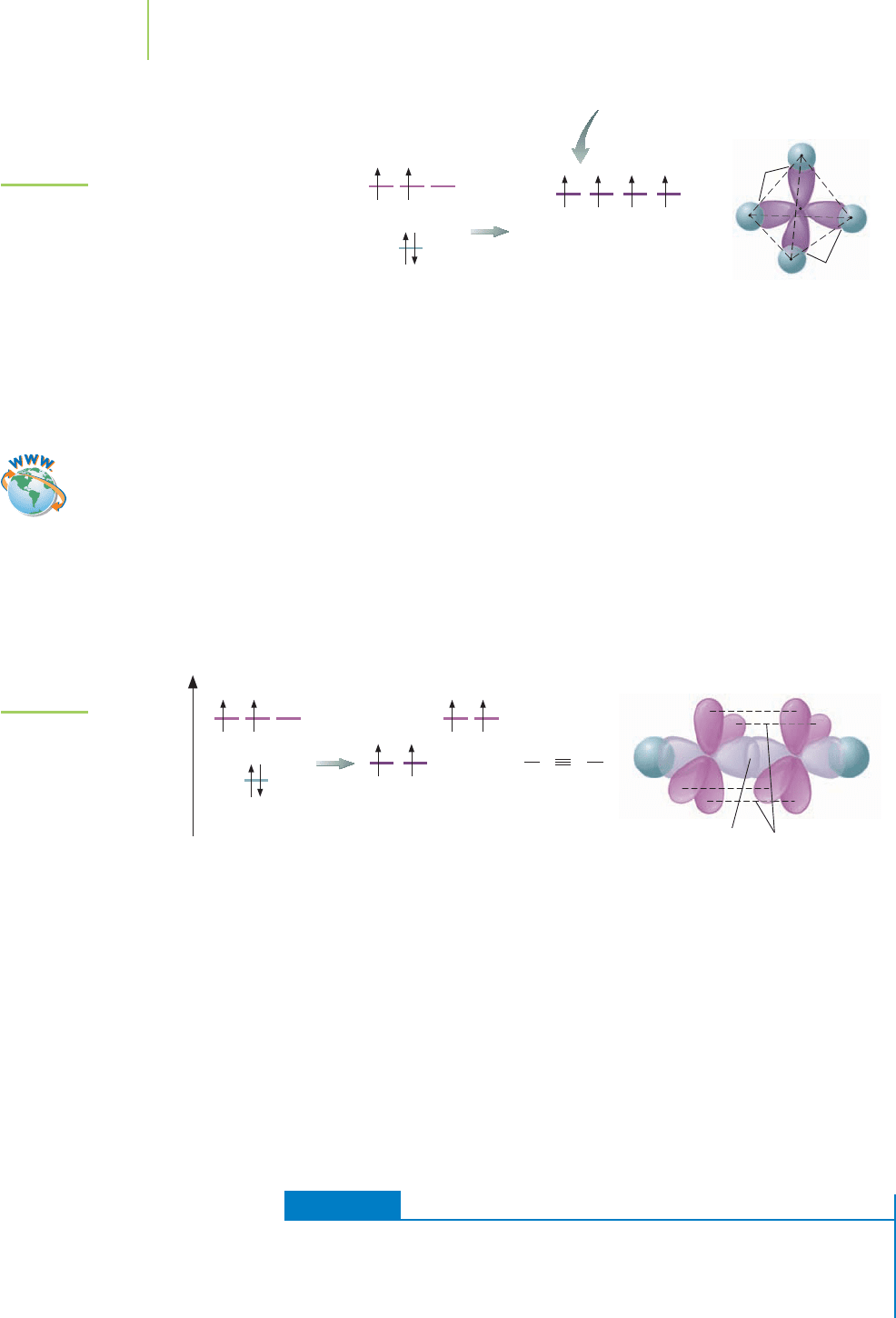
370 Chapter 9 Advanced Models of Bonding
FIGURE 9.17
Methane hybridization
and sigma bonds.
2p
2s
2p 2p 2p 2p
sp sp
Energy
HH
CC
π bondσ bond
FIGURE 9.18
Acetylene pi bonds.
There are two π bonds
in acetylene that result
from the overlap of two
p orbitals from each
carbon atom.
is an end-on overlap of an sp
3
orbital and an s orbital. The resulting σ bond does
not possess a nodal plane along the axis of the bond (Figure 9.17) and has a shape
reminiscent of a hot dog.
Nodal planes are flat, imaginary planes passing through
the bonded atoms where the orbital does not exist. An example of a nodal plane
is found in many molecules that contain double bonds.
Pi bonds (π bonds), which react with other molecules as if they are electron-
rich bonds, result from the side-to-side overlap of orbitals. This type of bond oc-
curs primarily when p orbitals on adjacent atoms overlap, as is found between
atoms containing a double or triple bond. The resulting π bond has one nodal
plane along the axis of the bond and has the shape of the two halves of a hot dog
bun separated by empty space. That is, there is a plane that exists between the
atoms that is not occupied by π electrons. Acetylene (C
2
H
2
) is a molecule that
contains two π bonds resulting from the overlap of p orbitals (Figure 9.18).
Why do we show the 2sp and 2p orbitals in the diagrams in Figure 9.18 with
one electron each? Shouldn’t we fill the 2sp orbitals before filling the slightly
higher energy 2p orbitals? Hund’s rule would seem to suggest this, but because the
energy difference between the hybridized and unhybridized orbitals of the same
shell is relatively small, the electrons can be temporarily placed in higher energy
2p orbitals prior to bond formation. The bonds that are created end up with lower
energies than they would have had in the hybridized orbitals. Keep in mind that
because each hybridized orbital will overlap to form a bond, no more than one
electron can be placed in each of the hybridized orbitals. The neighboring atom
will provide the second electron used in the bond. In addition, it is important to
note that although we have discussed the hybridization process as a series of steps,
no hybridization will take place without the formation of bonds. That is, in the
absence of any other atoms, hybridization does not occur in an individual atom.
EXERCISE 9.5 Polymers and Pi Bonds
Ethylene (C
2
H
4
) is used as the starting material for the preparation of polyethylene,
a common polymer used in the production of plastic bags, plastic sheeting, and the
like (see Chapter 13 for more on plastics). Describe the bonding patterns in ethyl-
ene using the valence bond theory.
Video Lesson: Pi Bonds
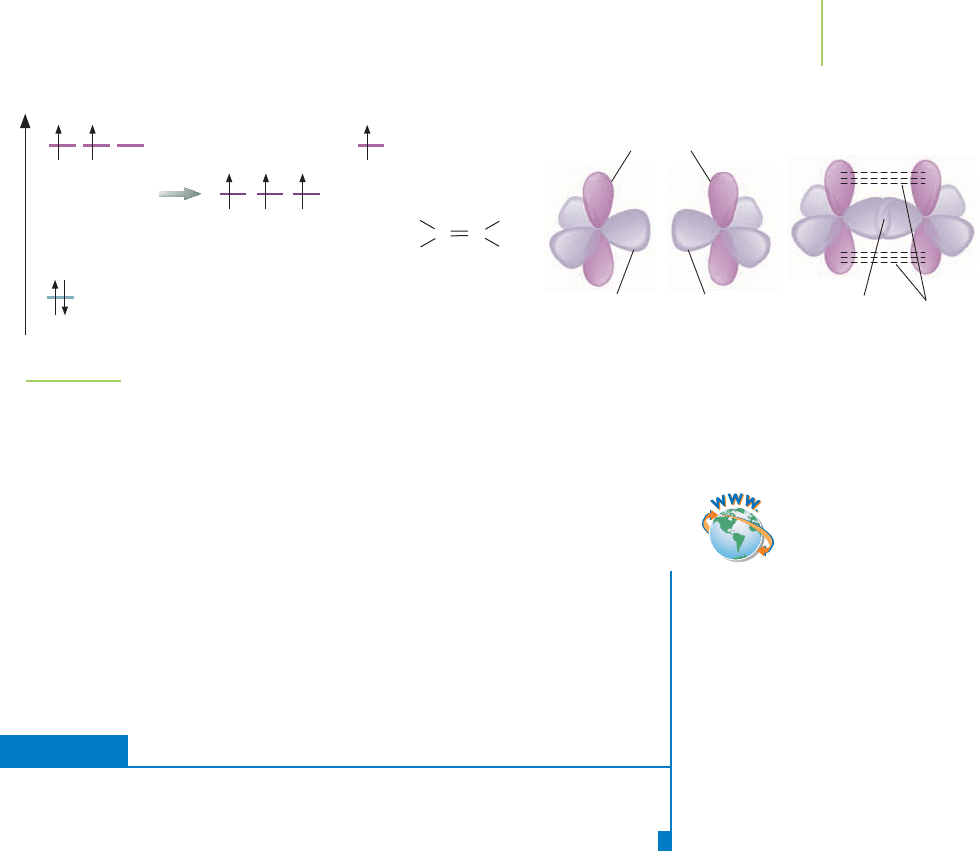
Solution
After hybridization of the two carbon atoms in ethylene, we observe that the 2sp
2
orbitals on the carbons can overlap to form a sigma bond. In addition, each carbon
atom still contains a half-filled 2p orbital. Such orbitals can overlap to create a pi
bond between the atoms. Ethylene, shown in Figure 9.19, has one pi bond and a
total of five sigma bonds.
PRACTICE 9.5
Describe the valence bond theory for formaldehyde (CH
2
O), a compound used in
the preservation of biological tissues.
See Problems 11, 12, 37–40, 96, and 99.
Application of Hybridization Theory
The hybridization of orbitals allows us to address the same geometric features
that are explained in the VSEPR approach to modeling. Why do we hybridize the
orbitals in water?
Does it give a better model? Valence bond theory indicates that
if we didn’t hybridize the orbitals of the central oxygen in water, there would still
be two bonds. However, the bonds that would result from the lack of hybridiza-
tion would have 90° angles between each other (overlap of a hydrogen s orbital
with an oxygen p orbital). Hybridization is necessary for the model of water to
agree with the experimentally measured bond angles.
The use of hybridized orbitals also provides information about the relative
lengths of bonds in molecules. We’ve already discussed how s–p orbital overlap
produces a bond that is longer than one containing s–s orbital overlap. This dis-
cussion can be carried further to illustrate the lengths of hybridized orbital
bonds. Table 9.4 lists the relative sizes of these orbitals and some features of the
resulting hybridization. From this table we see that the sp
3
hybrid orbital makes
bonds that are longer than the sp
2
. The sp
2
hybrid orbital is longer than the sp.Ap-
parently, mixing more p orbitals into the hybrid produces longer hybrid orbitals.
And we note that a bond made from sp
3
–sp
3
orbital overlap is longer than one
made from s–sp
3
overlap.The values in the table are average values (bond lengths
and bond angles) based on actual measurements from a collection of similar
molecules.
9.2 Hybridization 371
2p
2s
2p 2p 2p
sp
2
sp
2
sp
2
Energy
H
H
H
H
CC
Unhybridized p orbitals
π bondσ bond
sp
2
Hybrid orbitals
FIGURE 9.19
Ethylene and valence bond theory. The overlap of the orbitals between the carbons gives rise to a sigma
bond and a pi bond. The sigma bond results from 2sp
2
–2sp
2
overlap. The pi bond results from the side-to-
side overlap of the 2p orbitals.
Visualization: Formation of
CPC Double Bond in Ethylene

EXERCISE 9.6 Bond lengths of C—C Single Bonds
The Lewis dot structures of butane (often used as lighter fluid), 1–butene (a com-
pound used to make plastic wraps), and 1,3-butadiene (the starting material used to
make synthetic rubber for your car’s tires) are shown in Figure 9.20. Which has the
longest COC bond? Which has the shortest COC bond?
372 Chapter 9 Advanced Models of Bonding
CC
H
H
H
H
CH C
H
H
H
HH
Butane
FIGURE 9.20
Butane, 1-butene, and 1,3-butadiene.
(The bond length in question is indicated
with an arrow.)
First Thoughts
Our first goal here is to determine the hybridization of the atoms in each of the mol-
ecules. Then, using this information, we should put together a geometric picture of
each molecule that shows the types of orbital overlap that we expect for each bond.
Solution
The shortest COC bond is found in 1,3-butadiene. It results from the overlap of an
sp
2
hybridized orbital with another sp
2
hybridized orbital. The longest bond is
found in butane (sp
3
–sp
3
orbital overlap).
Further Insights
The COC bond length in 1,3-butadiene indicates that the electrons in the double
bonds can travel throughout the entire molecule. We can illustrate this by drawing
resonance structures showing a double bond between the two central carbon atoms.
PRACTICE 9.6
Which has a longer NOO bond length, CH
2
NOH or CH
3
NHOH?
See Problems 13–15.
Advantages and Disadvantages of Hybridization
We must gain some advantage from spending time developing the hybridized
model of a molecule. In fact, we do. With this model, we are able to explain bond
angles, the lengths of bonds in molecules, and the existence of pi bonds. Unfor-
tunately, valence bond theory and hybridization have some shortcomings. The
relative size of many bond lengths can be accurately predicted, though some are
“mystifyingly” unable to be accurately estimated. For example, why is the CPC
bond longer in 1,3-butadiene than in 1-butene? An even more refined picture of
the orbitals on the molecule needs to be considered.
Organic chemists do put hybridization to good use. Often they use it to
describe the three-dimensional structure of a molecule to others. This approach
enables organic chemists to talk to other organic chemists without drawing
C
HHHH
HH
CCC C
+
–
HHHH
HH
CCC C
+
+
–
–
HHHH
HH
CCC C
+
–
HHHH
HH
CCC
CCC
H
H
H
C
H
H
H
HH
1-Butene
CCC
H
H
H
C
H
HH
1,3-Butadiene
pictures on cocktail napkins. It also allows the organic chemist to describe spe-
cific structural features of a molecule that play an important role in the chemical
and physical properties of that molecule.
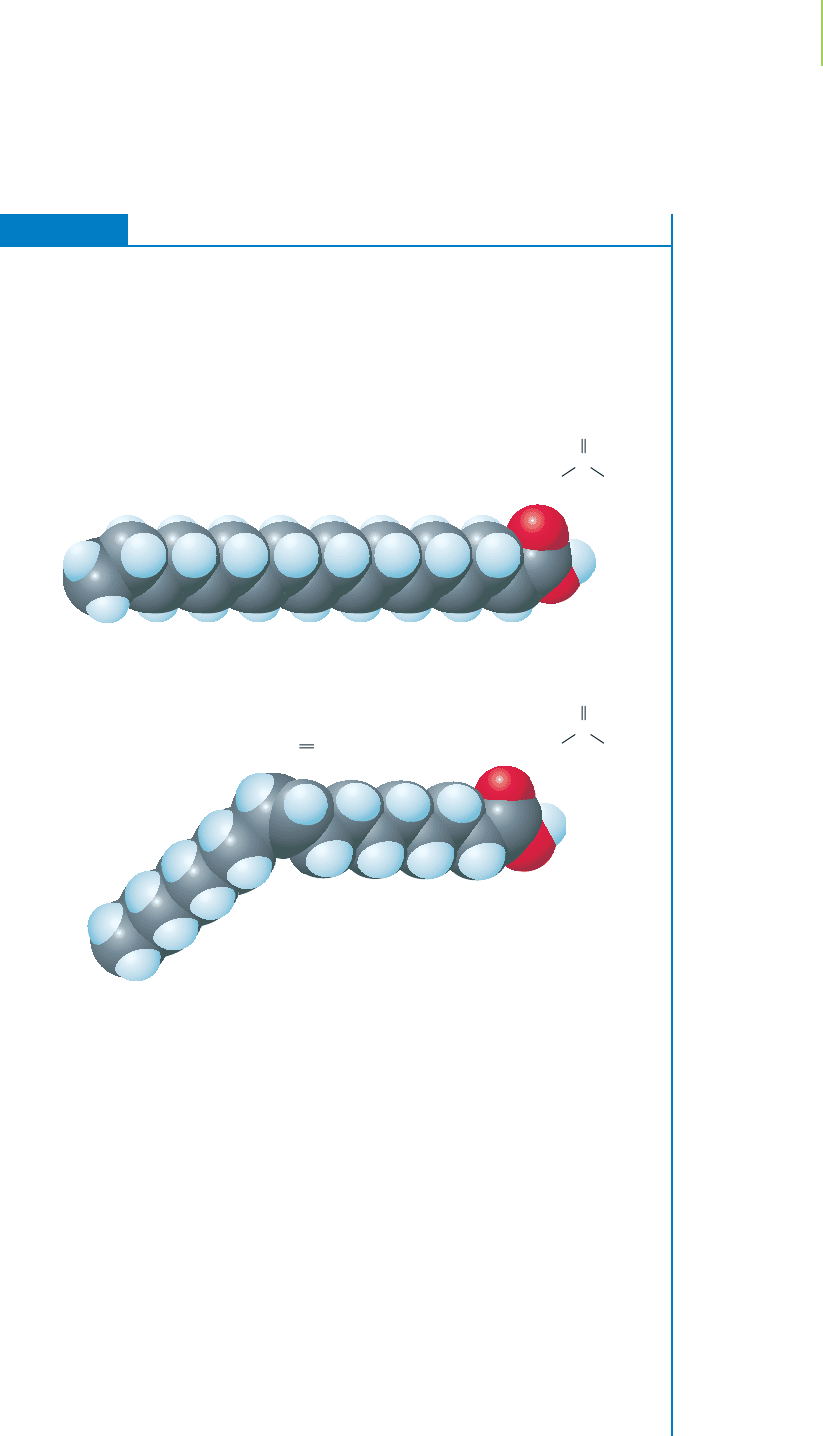
EXERCISE 9.7 Using Hybrid Orbital Theory: Will the Molecule Be Solid or Liquid?
Animal fats, such as lard, tend to be solid. Vegetable oils, such as corn oil, tend to be
liquid. Fats and oils are made up of compounds known as triacylglycerols. In turn,
the triacylglycerols are constructed from molecules known as fatty acids. Look at the
two fatty acids, stearic and oleic acids, depicted below. Describe the shapes of these
molecules using valence bond theory, and use this information to determine which
molecule is more likely to exist as a solid at room temperature.
9.2 Hybridization 373
Stearic acid
Oleic acid
CH
3
CH
2
CH
2
CH
2
CH
2
CH
2
CH
2
CH
2
CH
2
CH
2
CH
2
CH
2
CH
2
CH
2
CH
2
CH
2
CH
2
C
O
OH
CH
3
CH
2
CH
2
CH
2
CH
2
CH
2
CH
2
CH
2
CH CHCH
2
CH
2
CH
2
CH
2
CH
2
CH
2
CH
2
C
O
OH
First Thoughts
What makes a compound likely to be solid at room temperature? If the molecules
can pack easily and tightly together, they will be more likely to form a solid. If the
molecules are more rigid and less able to get close together, they will be less likely to
form a solid at room temperature.
Solution
Stearic acid is made up of 17 carbon atoms that are sp
3
hybridized and 1 carbon
atom that is sp
2
hybridized. The sp
3
hybridized carbons involve single bonds to ad-
jacent carbons and can rotate to form a zig-zag pattern of atoms. The sp
2
hybridized
carbon is more rigid in its trigonal planar configuration. Oleic acid contains mostly
sp
3
hybridized carbon atoms, but it also has three sp
2
hybridized carbons. The pres-
ence of two of the sp
2
hybridized atoms in the middle of the long carbon chain
causes a kink in the zig-zag structure. Steric acid can pack tightly with other steric
acid molecules, so it is a solid at room temperature. Oleic acid, because of its bent,
rigid structure doesn’t stack together well with other molecules. Oleic acid is a
liquid at room temperature.
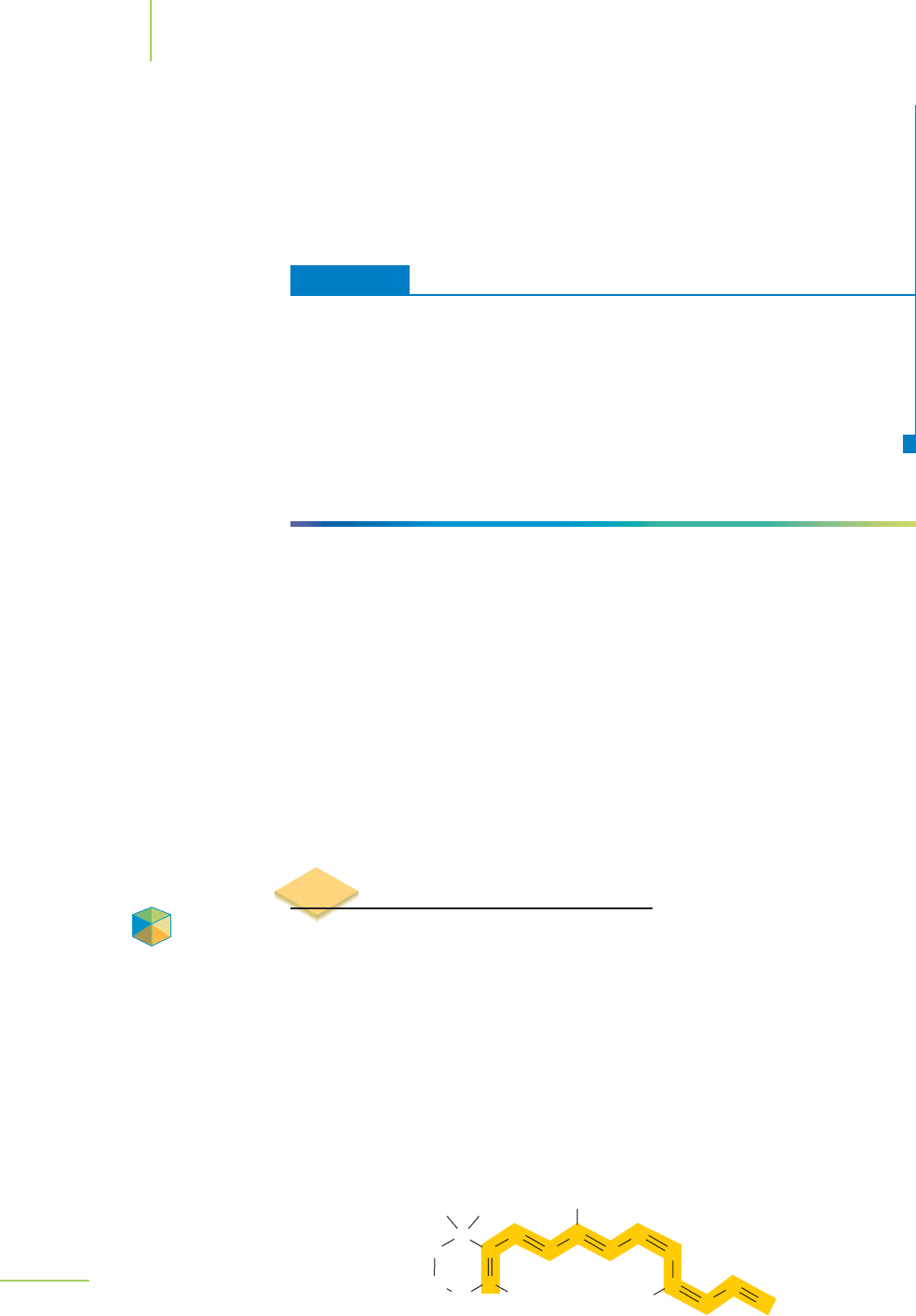
C
C
C
H
C
CH
2
CH
3
CH
3
CH
3
CH
2
CH
2
C
CH
3
C
H
H
C
CH
C
H
11-cis-Retinal
O
C
C
H
H
C
CH
3
Further Insights
Knowing the three-dimensional structure of a molecule can provide information
about the melting temperature of a molecule. But the three-dimensional structure
of a molecule can also yield a wealth of other information. Physical properties, such
as boiling point, melting point, color, taste, and smell, and chemical properties, such
as reactivity with acids or bases, are all dependent on the shape of the molecule.
PRACTICE 9.7
Describe the three-dimensional shape of each of the following molecules. Solely on
the basis of its shape, which do you predict will have the highest boiling point?
a. CH
3
CH
2
CH
2
CH
2
CH
3
(pentane)
b. CH
3
CH
2
CH(CH
3
)
2
(2-methylbutane)
c. C(CH
3
)
4
(2,2-dimethylpropane)
See Problems 41, 42, 47, 48, 53, and 54.
HERE’S WHAT WE KNOW SO FAR
■
We can mathematically combine two or more orbitals to provide new orbitals
of equal energy in the process of hybridization.
■
The models of many molecules agree with the experimentally measured bond
angles when hybridization is taken into account.
■
Although the hybridization process itself “runs uphill” energetically, the end
result is still energetically downhill.
■
Hybrid orbitals can be constructed to account for atoms that observe the octet
rule as well as for those with expanded octets.
■
The sigma (σ) bond does not possess a nodal plane along the axis of the bond
and has a shape reminiscent of a hot dog. A pi (π) bond results from the side-
to-side overlap of orbitals and is found between atoms containing a double or
triple bond. It has one nodal plane along the axis of the bond.
9.3 Molecular Orbital Theory
Let’s revisit the molecule of retinal (the light-absorbing portion of the rhodopsin
protein in our eyes) that we introduced in the chapter opener. 11-cis-Retinal is a
molecule containing an extended series of alternating single and double bonds
known as
conjugated π bonds (or conjugation), as shown in Figure 9.21. Electrons
in π bonds (whether conjugated or not) can absorb a photon of light. These elec-
trons become excited (more energetic) when the photon is absorbed and the elec-
trons are promoted to a higher energy state. The models we’ve already discussed
say nothing about these higher energy states. Here are the key ideas we will ex-
plore in this section:
1. Higher energy states can be reached by the absorption of energy.
2. All electrons in a molecule can absorb photons of light.
374 Chapter 9 Advanced Models of Bonding
Application
FIGURE 9.21
11-cis-retinal is a conjugated molecule. Note that there
are alternating single and double bonds through a large
portion of the molecule.

Antibonding
Bonding
Energy
In LCAO–MO theory, atomic orbitals are
added together, both constructively and
destructively, to make molecular orbitals.
The resulting bonding orbital is of lower
energy, and the antibonding orbital is of
higher energy, than the individual atomic
orbitals.
9.3 Molecular Orbital Theory
375
3. To become excited, core electrons require more energy (such as that of
X-rays) than do valence electrons (for which the energy of UV or visible light
is enough).
4. Sigma-bonding electrons require more energy (UV less than 200 nm) than
pi-bonding electrons (visible between 200 and 700 nm) to become excited.
5. Electrons in conjugated π bonds require even less energy than unconjugated
π bonds to promote an electron in a π bond to the higher energy state.
6. As the conjugated π system gets longer, the energy of the photon required to
excite the electrons is reduced, moving from the blue toward the red region
of the visible electromagnetic spectrum.
This final property is used by photography chemists in the design of mole-
cules that can absorb a particular wavelength of light. Molecular orbital theory
can also be used to tell us what happens to bonds within a molecule when they
absorb light, why hydrogen exists as a diatomic molecule and helium does not,
and why some molecules (such as O
2
) are attracted to magnetic fields and why
some molecules (such as N
2
) are not.
Molecular Orbital Theory Defined
At about the same time that Linus Pauling worked out valence bond theory,
Robert S. Mulliken (1896–1986) began thinking about how bonds could arise
from delocalized valence orbitals. Erwin Schrödinger (1887–1961) further devel-
oped this approach by devising a mathematical equation that described the hy-
drogen atom. This theory, known as
molecular orbital (MO) theory, is based on the
principles of quantum mechanics that we discussed in Chapter 6. It treats elec-
trons not as particles, but as waves that encompass the entire molecule. As in the
quantum mechanical description of atomic orbitals, molecular orbitals encircle
the atoms in a molecule. The Schrödinger equation defines the energy of each of
the orbitals of an atom or molecule. Unfortunately, the Schrödinger equation
cannot be solved exactly, except for a few very simple systems, so we usually make
some approximations that allow us to arrive at a usable solution. Probably the
most commonly used approximation is known as the
linear combination of atomic
orbitals–molecular orbitals (LCAO–MO) theory
. In this theory, atomic orbitals are
added together (both constructively and destructively) to make molecular
orbitals.
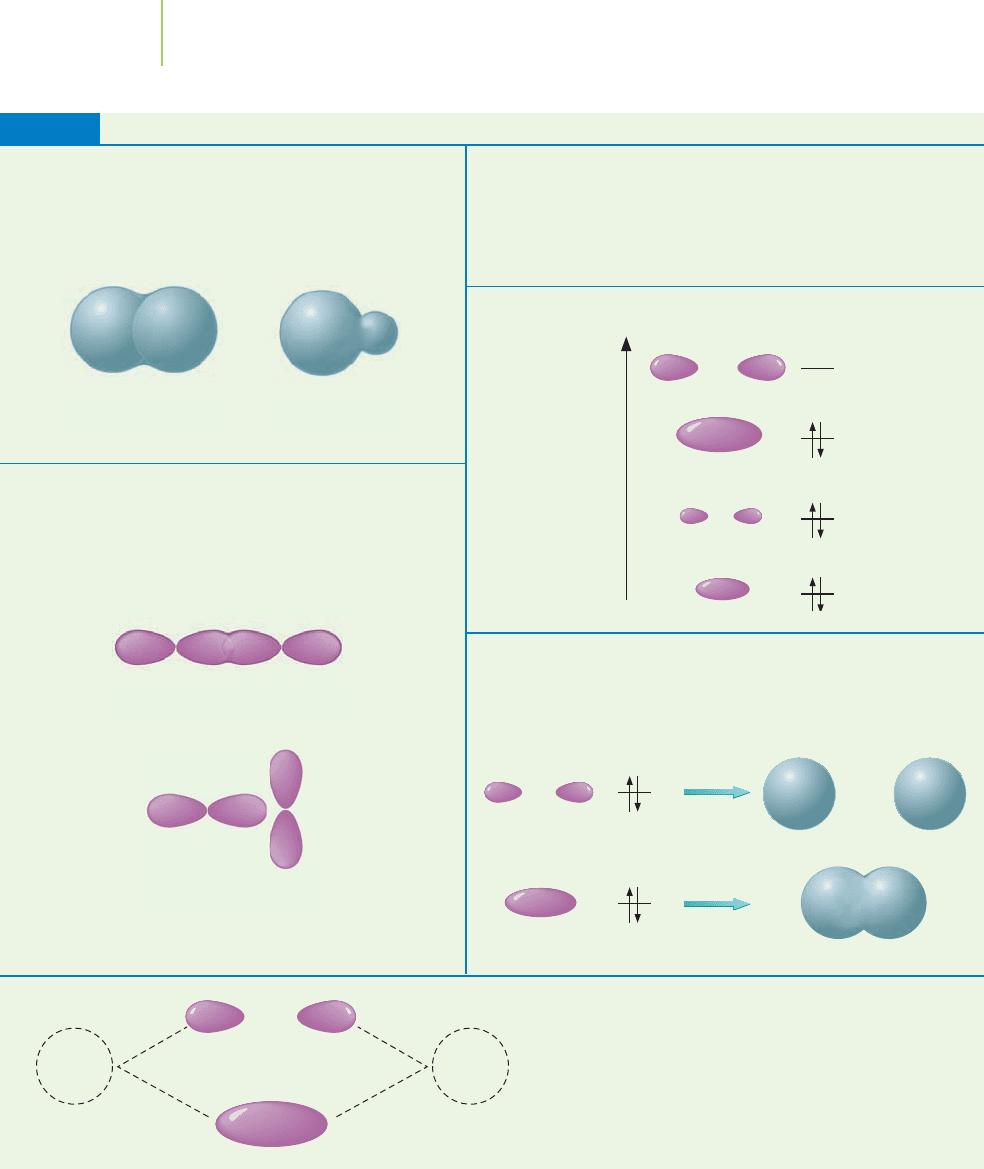
We must raise several points about the formation of molecular orbitals from
atomic orbitals (see Table 9.5). The most important point is that the combination
of two orbitals gives two new orbitals, just as in the hybridization of atomic or-
bitals. One of the new molecular orbitals, called the
bonding orbital, results from
the addition of two overlapping atomic orbitals; the other, called the
antibonding
orbital
, results from the subtraction of two overlapping atomic orbitals. The
bonding orbital is lower in energy than either of the two atomic orbitals (the for-
mation of a molecular orbital with lower energy than the atomic orbitals drives
the formation of the bond). The bonding orbital indicates that there is some elec-
tron density between adjacent nuclei (a bond exists). The antibonding orbital is
higher in energy than the two atomic orbitals from which it is formed and is typ-
ically represented with an asterisk (
∗
) to distinguish it from the bonding orbital.
The antibonding orbital indicates a lack of electron density between adjacent nu-
clei (no bond exists). Each new molecular orbital (both bonding and antibond-
ing) can contain two electrons.
A similarly important point in mixing atomic orbitals to make molecular or-
bitals is that only atomic orbitals of similar symmetry (shape and orientation)
and energy provide significant overlap. This rule means that only 1s orbitals over-
lap to a great degree with 1s orbitals. The 2p
z
orbital overlaps best with a 2p
z
or-
bital. Their symmetry and size (i.e., energy) are similar. The 1s orbital doesn’t
Video Lesson: Molecular Orbital
Theory
overlap well with a 3s orbital (the size isn’t a good match). The 2p
x
orbital does
not overlap well with the 2p
z
orbital (the symmetry doesn’t allow them to line up
properly).
We can think of this by imagining that overlapping orbitals are a game of
Tetris. In Figure 9.22, we can see that the best game piece to use to fill the 4 × 4
hole at the bottom of the screen is a 4 × 4 rectangle. A 3 × 3 rectangle wouldn’t
do a very good job of filling the hole, just as a 1s orbital and a 3s orbital don’t
overlap very well. They have the same symmetry (shape), but the size isn’t right.
376 Chapter 9 Advanced Models of Bonding
Key Features of MO Diagram Construction
TABLE 9.5
2p
x
2p
x
Good overlap
Poor overlap
2p
x
2p
z
Energy
2s 2s
Good overlap
Poor overlap
2s 1s
We restrict ourselves by insisting that only orbitals of
similar energy can mix to make molecular orbitals
(MOs). The 2s orbital, for example, can mix with a 2s
orbital but does not mix well with the 1s orbital.
Mixing atomic orbitals gives the same number of MOs.
• The bonding orbital is lower in energy than the atomic
orbitals from which it was made.
• The antibonding orbital is higher in energy than the
atomic orbitals from which it was made.
Electrons are placed in MOs in order of increasing energy.
Only orbitals that exhibit symmetry (that is, they are
similar in shape and orientation) can mix to make
MOs. For example, the 2p
x
orbital cannot mix with
the 2p
z
orbital, since they are oriented differently.
Each MO can hold two electrons with opposite spin.
• Electrons that are placed in bonding MOs promote
bonding.
• Electrons that are placed in antibonding MOs favor
separated atoms.
After mixing of the atomic orbitals, they
cease to exist. Only the molecular orbitals
remain.
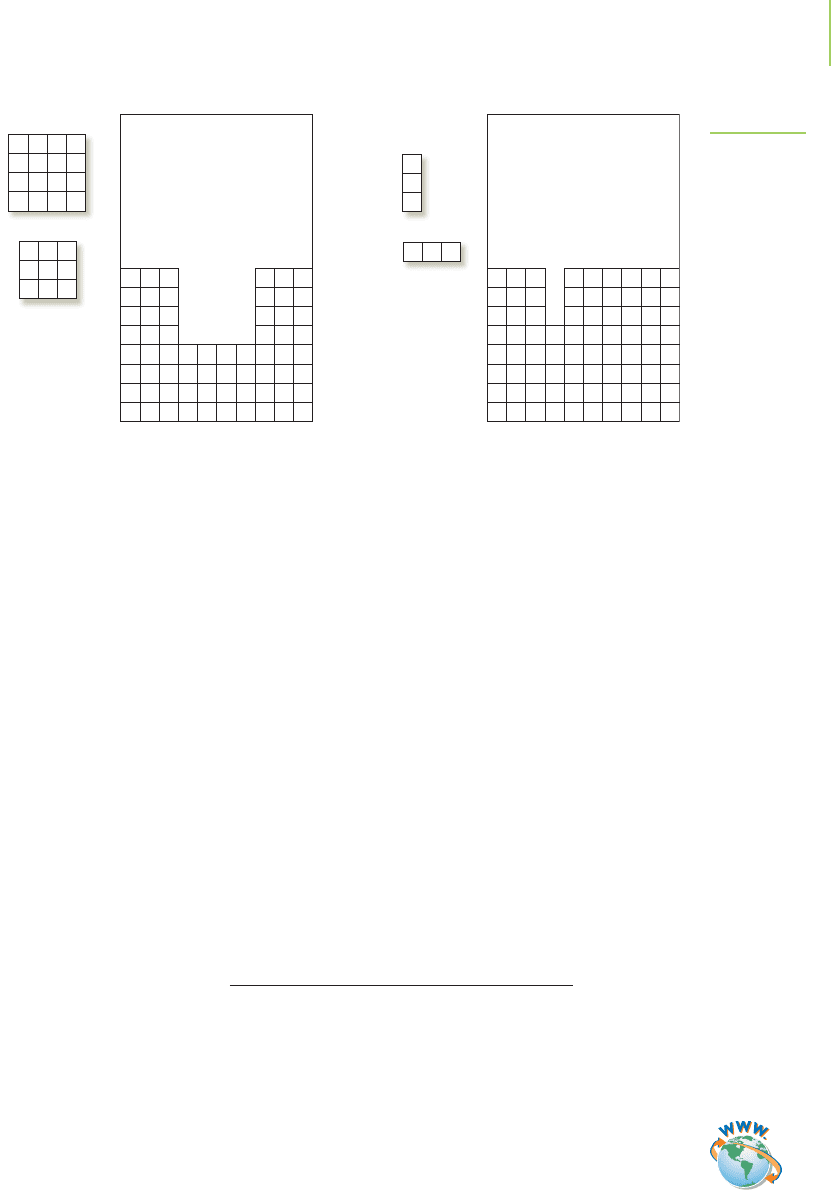
In the second image of Figure 9.22, we need a vertical 1 × 3 rectangle to fill the
vertical 1 × 3 hole. A horizontal rectangle of the same size wouldn’t work, just as
a 2p
z
orbital doesn’t overlap with a 2p
x
orbital. The symmetry (shape) of the two
orbitals doesn’t match, even though their size does.
Shapes of Orbitals
What about the shapes of the molecular orbitals? Molecular orbitals encompass
entire molecules, and the shapes of the molecular orbitals often look similar to
portions of the entire molecule. We know about their existence by calculation
using some approximations of the Schrödinger equation, but how do we really
know what the shape of a molecule is? X-ray crystallography (see Section 13.1) is
one of the methods used to take a “snapshot” of a molecule. But it relies on de-
termining the average location of the atoms in a crystal. The scanning tunneling
microscope that we discussed in Chapter 6 may actually be the closest we can get
to taking a picture of a single molecule.
The strength of the bond between two atoms can be represented by the
bond
order
, the number of electrons in bonding orbitals minus the number of elec-
trons in antibonding orbitals, divided by 2.
Bond order =
bonding electrons − antibonding electrons
2
A larger bond order indicates a greater bond strength. The bond order typically
agrees with the Lewis dot structure’s expected number of bonds between adjacent
atoms. However, the bond order between two atoms doesn’t have to be a whole
number.
To summarize, molecular orbital theory holds that when the atoms of a mol-
ecule come together, atomic orbitals on each atom that are similar in symmetry
and energy not only overlap but are transformed into a series of new orbitals that
surround the entire molecule. These molecular orbitals have completely different
shapes, sizes, and energies than the atomic orbitals from which they came.
Although the atomic orbitals cease to exist after the creation of the molecular
orbitals, the new molecular orbitals follow the same rules that guide us in placing
electrons in the atomic orbitals.
MO Diagrams
Just as the civil engineer diagrams the layout of a building with a blueprint, we
represent the placement of electrons in molecular orbitals with our own type of
blueprints called
molecular orbital (MO) diagrams. These diagrams graphically
9.3 Molecular Orbital Theory 377
(a) (b)
FIGURE 9.22
Tetris analogy to overlapping orbitals:
(a) The 4 × 4 square piece has the
same size and shape as the hole. The
3 × 3 square has the same shape but
the wrong size. (b) The 1 × 3 rectangle
has the same size and shape as the
hole. The horizontal 1 × 3 rectangle has
the same size but is the wrong orienta-
tion to fit into the hole.
Visualization: Pi Bonding and
Antibonding Orbitals
