Kelter P., Mosher M., Scott A. Chemistry. The Practical Science

Подождите немного. Документ загружается.

238 Chapter 6 Quantum Chemistry: The Strange World of Atoms

from the tip to the material set up an electric current (the “tunneling current”)

that increases as we bring the tip closer to the atom and decreases as we pull away.

This allows us to image the atomic positions (though only to a level of precision

limited by Heisenberg’s uncertainty principle) by scanning the tip over the mate-

rial and seeing just what kind of overlap we get. An example image is shown in

Figure 6.27. The bigger the tunneling current is, the more electrons there are in

proximity to the tip. As we pull the tip away from the surface, the tunneling cur-

rent falls off exponentially with distance. Because we assume that the atom is in

the center of the greatest electron density, we get an image of the atoms at the sur-

face of the material. The image that results from these measurements conveys

information about the positions of electrons in atoms. These are not pho-

tographs of atoms, but they are impressive testimony to our ability to detect

where individual atoms are, within the constraints of the uncertainty principle.

Even more impressive, the image that opens this chapter shows the genuine wave-

like nature of matter at the quantum scale. Look at the ripples: direct evidence

that wave–particle duality is real!

The STM is a practical application of the fact that we don’t actually have a nat-

ural end to the radial distribution function. It goes on forever and ever, just with

increasingly smaller and smaller amplitude. According to classical mechanics the

STM should not work, because electrons should not be able to “tunnel” into

the places classical mechanics says they cannot go. The STM is practical proof

that quantum mechanics is a valid description of nature.

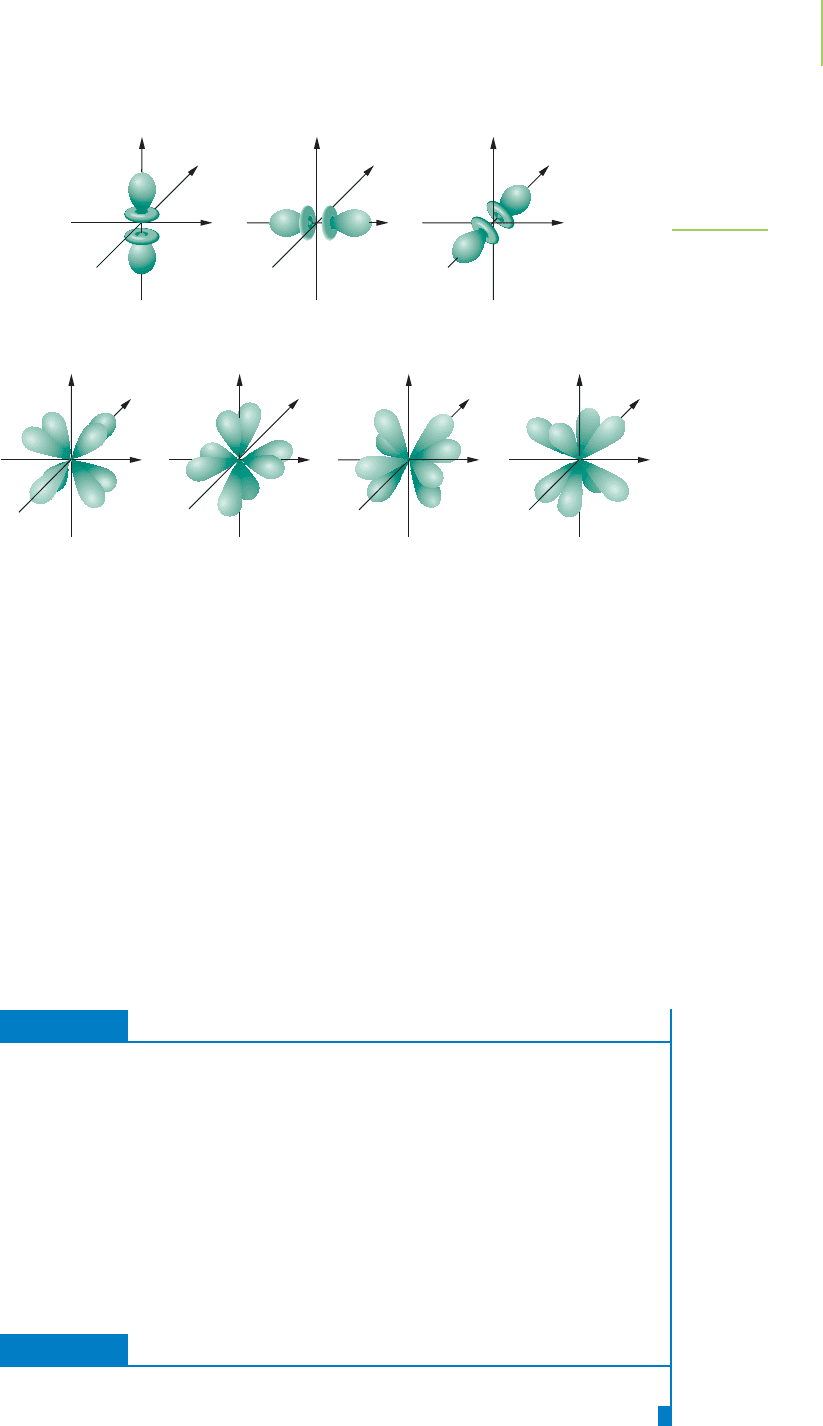
s Orbitals

What can we say about the shapes of the orbitals within an atom? The orbital

shown in Figure 6.26 that has l = 0 is radially symmetric and has a spherical

shape. That is, as we look out from the nucleus, the probability distribution func-

tion looks the same in every direction and varies only with r, the distance from

the nucleus. All orbitals with l = 0 are called

s orbitals and can be written as s.The

principal quantum number is added to this as a preﬁx when we write the name of

this speciﬁc orbital. For example, when n = 1 and l = 0, we write 1s. When n = 2

and l =0, we write 2s, and so on. The 1s orbital, with n =1, has no nodes and rep-

resents the lowest energy level, or ground state, for an electron in a hydrogen

atom. The 2s orbital has one node that is concentric around the nucleus. The 3s

orbital has two radial nodes, the 4s has three, and so on, with the number of con-

centric nodes increasing along with the principal quantum number.

The “solid spheres”of Figure 6.28 are useful in comparing relative sizes. As we

expect, the 1s orbital is the smallest, and the size increases as n increases. This

representation does not give us any help in visualizing the nodes present; the

two-dimensional cross sections are more helpful in this respect. The last method

of representing the s orbitals takes a more probabilistic approach and uses a gray

scale to show where the probability of ﬁnding the electron is large and where it is

small. The nodes are indicated by the lightest part of the picture. All s orbitals are

spherical, with the number of radial nodes increasing from zero in the 1s orbital

to n − 1 in the ns orbital. Remember that s orbitals all have orbital angular mo-

mentum quantum numbers of l = 0 and magnetic quantum numbers of m

= 0.

We still have to consider the Heisenberg uncertainty principle as we construct

our pictures. In order to draw sensible pictures of atomic sizes, we arbitrarily

assign the boundary of an atom to lie at some distance r from the center of the

atom, so that when we look for the electron within that value of r from the

nucleus, we ﬁnd the electron a large portion (90%) of the time. We show the 1s,

2s, and 3s orbitals in Figure 6.28 at the 90% probability distribution function for

the electron and in several different formats, each of which is meant to emphasize

some aspect of the orbital shape.

An s orbital.

Visualization: 1

Orbital



n = 3, l = 0

n = 2, l = 0

Node

n = 1, l = 0

(a) (b) (c)

FIGURE 6.29

The 2p

,2p

, and 2p

spatial component

of the hydrogen atomic orbitals at 90%

probability.

6.10 Atomic Orbitals

239

FIGURE 6.30

The location of the planar node found in

the 2p

orbital. Although n = 2 is used in

the example, all p orbitals have a single

planar node in an analogous position.

FIGURE 6.28

The 1s,2s, and 3s spatial component of

the hydrogen atomic orbitals at 90%

probability. Note the presence of nodes

in the cutaway plots.

FIGURE 6.31

The 2p

and 3p

spatial component of the hy-

drogen atomic orbitals at 90% probability.

p Orbitals

For orbitals with l = 1, which are known as p orbitals are abbreviated p, we have

a different spatial arrangement, as shown in Figure 6.29. Again we use the

convention of writing the principal quantum number as a preﬁx to the letter ab-

breviation for the orbital. However, because l = 1 allows for three possible m

values (+1, 0, and −1), there will be three degenerate orbitals that are symmetri-

cally equivalent. We can choose to orient the three equivalent orbitals along the x,

y, and z axes, and when we do so, we call them the 2p

,2p

, and 2p

orbitals. This

is shown for the lowest-energy 2p orbitals in Figure 6.29. The 2p orbitals have no

radial nodes, but each does have a planar node, as illustrated in Figure 6.30. For

the 2p

orbital, this node is the yz plane; for the 2p

orbital, this node is the xz

plane; and for the 2p

orbital, this node is the xy plane. We have set the size of the

orbital to include 90% of the probability for ﬁnding the electron within it, just as

we did with the s orbitals.

When we increase the primary quantum number to n = 3, we have three 3p

orbitals with the same kind of planar node structure (Figure 6.31), but now we also

have a radial node. The three 4p orbitals have the planar node plus two radial nodes,

the three 5p orbitals have the planar node plus three radial nodes, and so on.

Visualization: 2

Orbital

Visualization: 2

Orbital

Visualization: 2

Orbital

–y

FIGURE 6.32

The 3d

,3d

−y

, and 3d

spatial component

of the hydrogen atomic orbitals at 90% probability.

240 Chapter 6 Quantum Chemistry: The Strange World of Atoms

d Orbitals

Orbitals with l = 2 are called d orbitals (abbreviated as d) and have two nonradial

nodes. The ﬁrst set of quantum numbers for which l can equal 2 occurs when

n = 3. Five d orbitals occur, because m

takes the values of 2, 1, 0, −1, −2 when

l = 2. For all but the m

= 0 d orbital, the nodes are planar and are at 90° to each

other. These orbitals have four lobes that are labeled d

, d

, and d

−

and

are oriented as shown in Figure 6.32. The remaining d orbital is labeled d

and looks a bit different but is equivalent in energy (degenerate) to the other four

d orbitals provided that it has the same principal quantum number. The d

or-

bital has two hyperbolic nodes that give the orbital a dumbbell structure with a

little toroidal “donut.” When n = 3, no radial nodes occur, as shown in Figure

6.33, but n = 4 has one radial node, n = 5 has two radial nodes, and d orbitals

with higher principal quantum numbers have n − 3 radial nodes.

Nodal

surface

Nodal

plane

–y

FIGURE 6.33

The location of the two planar nodes found in the

,3d

, and 3d

−y

lobes and the two hy-

perbolic nodes orbitals of the 3d

lobe. Although

n = 3 is used in the example, all d orbitals have

two planar nodes in analogous positions.

Visualization: 3

−

Orbital

Visualization: 3

Orbital

Visualization: 3

Orbital

Visualization: 3

Orbital

Visualization: 3

Orbital

6.10 Atomic Orbitals 241

f Orbitals

Much of our use of orbitals focuses on the s, p, and d levels. The one exception is

the

f orbitals (abbreviated f ) with l = 3 and m

= 3, 2, 1, 0, −1, −2 , −3. These

seven orbitals will be used in our description of heavy atoms, such as those in the

lanthanide and actinide series of the periodic table. They are shown in

Figure 6.34. Note that they are multilobed and geometrically quite complicated.

At last we have arrived at our current “quantum mechanical” or “wave me-

chanical” model of atomic structure, although we can depict it only by showing

the places around the nucleus where an electron in any orbital will most probably

be found. In painting a more accurate picture of what electrons are doing, we

have had to acknowledge the uncertainty and strangeness—the funny things that

happen—down in the quantum world.

EXERCISE 6.7 Quantum Numbers

Indicate the possible values for the quantum numbers (n, l, m

) that would corre-

spond to the 3d orbital.

Solution

A single 3d orbital would correspond to one of these sets of quantum numbers:

n = 3, l = 2, m

=−2

n = 3, l = 2, m

=−1

n = 3, l = 2, m

= 0

n = 3, l = 2, m

=+1

n = 3, l = 2, m

=+2

PRACTICE 6.7

Indicate the orbital described by the quantum numbers, n = 2, l = 1, m

= 0.

See Problems 86 and 117.

yy y y

yyy

– —

xyz

y(x

– z

)

x(z

– y

)

z(x

– y

)

– —

2 f

– —

FIGURE 6.34

The 4f spatial component of the hydrogen

atomic orbitals at 90% probability.

(b)

(a)

–

242 Chapter 6 Quantum Chemistry: The Strange World of Atoms

6.11 Electron Spin and

the Pauli Exclusion Principle

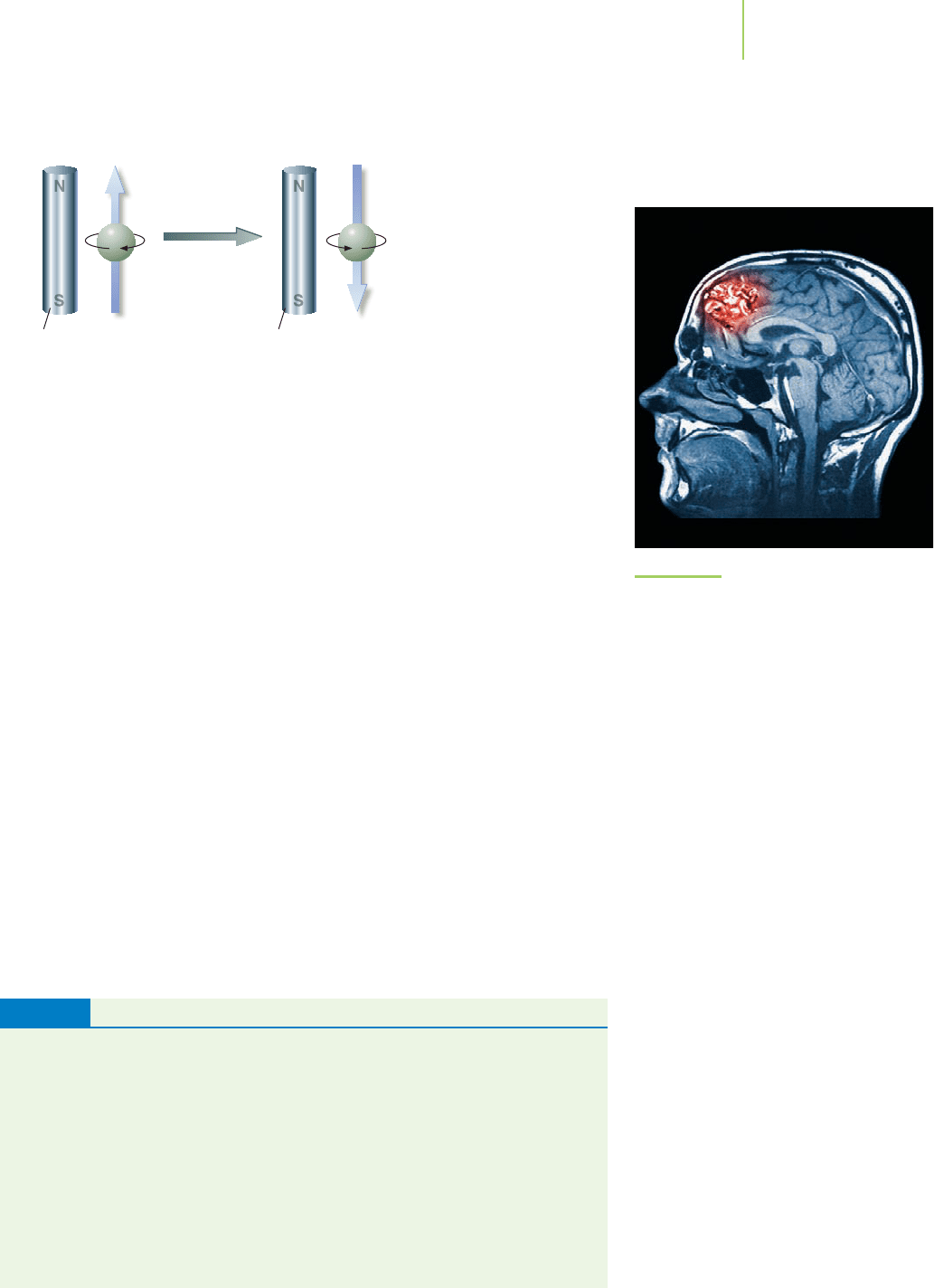
An electron behaves as though it were spinning about an axis. A “spin” in one

direction corresponds to an electron spin quantum number (m

) of +

, and a

“spin” in the opposite direction corresponds to an electron spin quantum

number (m

) of −

. These are the only two values of m

available; in other

words, spin is quantized into these two states, and an electron must be in one of

them. The “spin” of an electron makes the electron behave as though it were a tiny

magnet. For example, if we put hydrogen atoms into a magnetic ﬁeld, electrons

with m

, called the “up” state, will line up parallel to the ﬁeld; and those with

=−

, called the “down” state, will line up antiparallel to it, as shown in

Figure 6.35. We sometimes represent the up state by an arrow pointing up:

↑

Similarly, the down state is represented by an arrow pointing down:

↓

One vital consequence of this idea of electron “spin” is that it allows two elec-

trons to occupy the same atomic orbital. Wolfgang Pauli, in 1925, proposed a rule

that allows only two electrons to occupy the same atomic orbital. According to

the

Pauli exclusion principle, no two electrons can have the same set of the four

quantum numbers (n, l, m

, and m

) in a given atom. What does this tell us about

the electronic structure of the atom?

For two electrons to occupy the same orbital,

they must have the same values for the quantum numbers n, l, and m

. The only

way that two electrons can have these quantum numbers is if their spin quantum

numbers (m

) are different. In essence, one of the electrons in the orbital is in the

spin up state, and the other is in the spin down state. Because it requires four quan-

tum numbers to describe an electron on an atom, it is not possible for more than two

electrons to occupy the same orbital.

Nuclear Spin and Magnetic

Resonance Imaging

An MRI scanner consists of a large magnet with a cylindrical tube bored through

the center. An example is shown in Figure 6.36. When a person is scanned, the

body part to be imaged needs to be in the center of the magnetic ﬁeld. The tech-

nique focuses on the nuclei of all of the hydrogen atoms in the body, because they

have a relatively large magnetic moment (a measure describing the magnitude

and direction of the nuclei’s magnetic ﬁeld). Placing the body in the magnet

causes the hydrogen nuclei to align with the magnetic ﬁeld. Just as with electrons,

there are nuclei with both up and down “spins,” so most of the nuclear “spins”

cancel each other out. But there are enough “unpaired” nuclei to result in a nice

image.

The image is created by directing radio frequency pulses toward the body part

to be examined. The radio pulses produce a miniature magnetic ﬁeld aligned in a

direction perpendicular to the ﬁeld of the magnet around the

body. This miniature magnetic ﬁeld disrupts the alignment of

the atoms in the body part. The atoms are then said to occupy

an excited state. When the radio pulse is turned off, the atoms

relax to their original state of alignment with the magnet and

release energy. The energy is detected by the MRI and con-

verted into an image of the body part.

How does the computer in the MRI distinguish the struc-

tures in the body? It does so on the basis of the amount of

time it takes for the excited hydrogen nuclei to relax back to

their original alignment with the external magnetic ﬁeld. The

realignment of the excited nuclei can last anywhere from a

few hundred milliseconds to a few seconds. The time it takes

Wolfgang Ernst Pauli (1900–1958) was

awarded the 1945 Nobel Prize in physics

for his discovery of what we now know

as the Pauli exclusion principle.

FIGURE 6.35

Electrons in the spin up and

spin down states.

Application

HEMICAL ENCOUNTERS:

Nuclear Spin and

Magnetic Resonance

Imaging

FIGURE 6.36

MRI scanner.

Video Lesson: Understanding

Electron Spin

6.11 Electron Spin and the Pauli Exclusion Principle 243

to realign is heavily dependent on the environment surrounding the hydrogen

nuclei. For example, hydrogen nuclei in water (which is the primary component

in blood and spinal ﬂuid) relax much more rapidly than hydrogen nuclei that

make up tissues, which in turn are faster than hydrogen atoms in fats. The differ-

ence is primarily due to the fact that hydrogen atoms are attached to different

types of atoms in each of these three components of the body. It is the variation

in relaxation times, combined with the differing concentrations of hydrogen

atoms in different tissues and body ﬂuids, that allows for the exceptional contrast

observed using this technique. Figure 6.37 shows an MRI image of a brain, where

color has been added to help distinguish the different tissues. This image can be

used to locate the position of a brain tumor and the major blood vessels leading

to it. MRI scanners are used to image many different areas of the body without

the use of invasive surgeries.

Reviewing the Signiﬁcance

of Quantum Numbers

We have seen that the four quantum numbers in any electron’s wave function

specify everything we need to know about the electron’s location in the atom.

They are a bit like an electron’s address in the atom. Table 6.5 summarizes the

signiﬁcance of all the quantum numbers.

External

Low Energy High Energy

+ Energy

External

Adding energy to a nucleus in a magnetic ﬁeld can cause it to

change its orientation with the ﬁeld. After time has passed, the

excited nucleus returns to the low energy state and emits a

photon of energy in the radio frequency range.

FIGURE 6.37

MRI brain image.

The Quantum Numbers

n = principal quantum number Indicates which of the major energy levels or

electron shells an orbital is in. Also, the larger

the value of n, the greater the total volume of the

orbital

l = angular momentum Indicates the shape of the orbital and which

quantum number quantum number type of subshell the orbital is

in, which will be an s, p, d,or f subshell

= magnetic quantum number Quantum number indicates the orientation of

the orbital in space

= electron spin quantum Indicates the orientation of the spin of the

number electron in the orbital

TABLE 6.5

244 Chapter 6 Quantum Chemistry: The Strange World of Atoms

6.12 Orbitals and Energy Levels

in Multielectron Atoms

Unfortunately, the orbitals calculated in the manner that we have discussed are

only absolutely correct for one-electron atoms and ions. You can use them for

hydrogen and its isotopes deuterium and tritium.You can also use them for He

, or even Hg

79+

if you adapt the equation slightly.

Problems arise when you put a second electron into an atom or ion. Because

the two electrons have the same charge, they repel each other. The interaction

between the two electrons makes it impossible to solve for their energies and

orbital wave functions exactly. Fortunately, ways exist to approximate the correct

energies and electron orbitals. The approximations also work for atoms contain-

ing three or more electrons, and the results can be quite good. How do we

describe the orbitals on an atom with more than one electron? We take the

hydrogen atomic orbitals, which are approximately correct because they describe

the effect the nucleus has on a single electron, and we change them a little to ap-

proximate the effect of other electrons. The results are useful both because they

accurately predict the physical properties of atoms, such as ionization energies

and emission spectra, and because we can use the multielectron orbitals to form

molecular orbitals, occupied by electrons in molecules (discussed in Chapter 9).

The shapes we derive for orbitals in multielectron atoms are very similar to

those in the hydrogen atom. Helium contains a 1s orbital, a 2s orbital, three 2p

orbitals, and so on, just as we found previously for the hydrogen atom. Each of

these can hold up to two electrons, one with spin up and one with spin down.

The four quantum numbers n, l, m

, and m

are called the principal, angular mo-

mentum, orbital angular momentum, and spin angular momentum

quantum numbers, just as before. The total number of nodes is n − 1,

and the number of nonradial nodes is n − l − 1, just as for the hydro-

gen atom. The kinds of the nodes and their approximate positions are

the same, and the shapes of the orbitals are similar enough that we can

use the same pictures we used above.

The one thing that will be different is the energies of the electron or-

bitals. These are so complicated that we will not be able to calculate

meaningful values for them without the aid of a computer, so we will

talk about energy only qualitatively here. One big difference in or-

bital energy levels is that whereas the energy depends only on the

principal quantum number, n, for the hydrogen atom, levels with dif-

ferent l values will now have different energies for the multielectron

atom.

This is because of something called

electron shielding (it is also known as elec-

tron screening). When a second electron is present in an atom, some of the time

this electron is between the ﬁrst electron and the nucleus. Because electrons are

negatively charged, the positive nuclear charge experienced by the ﬁrst electron is

smaller that it otherwise would be, and the attractive force between that electron

and the nucleus is decreased proportionately. The ﬁrst electron also sometimes

spends time closer to the nucleus than its partner, and when this happens, that

second electron will be shielded too. For the two 1s electrons in helium, both are

shielded the same amount, and they remain degenerate.

When we focus on orbitals with different n and/or different l values, all elec-

trons in an atom shield all other electrons, but not necessarily to the same extent.

The 2s electrons are, on average, closer to the nucleus than are 2p electrons, as

shown in Figure 6.38, and the 2s electrons will screen the 2p electrons far better

than the 2p will shield the 2s electrons. The nuclear charge will therefore seem to

be smaller to the 2p electrons than to the 2s electrons as a result of the greater

shielding. Because the apparent nuclear charge has been decreased, the attractive

Nucleus

Electrons

Repulsion

Attraction

The outer electrons are shielded from the charge

of the nucleus by electrons closer to the nucleus.

Probability

Distance from nucleus

2s2p

FIGURE 6.38

The relative distance from the nucleus of

the electron density in the 2s and 2p

orbitals.

Video Lesson: Electron Shielding

6.13 Electron Conﬁgurations and the Aufbau Principle 245

Energy (kJ mol

–1

)

480

960

1440

1920

2400

2880

3360

3840

H He Li Be B C N O F Ne Na

FIGURE 6.39

Relative energy levels for multielectron atoms. The relative placement of the energies of the orbitals is only approxi-

mate and varies with Z, the nuclear charge, which increases to the right across the periodic table.

forces between the nucleus and the electron will also decrease. The bottom line is

that the 2p electrons will no longer be as low in energy as the 2s electrons. This is

shown schematically in Figure 6.39. The 2p

,2p

, and 2p

orbitals will still be de-

generate, however, because they are all at the same average distance from the nu-

cleus and will all experience the same shielding from other electrons in the atom.

For n =3, the next principal quantum number up in energy, the 3s, will be lower

in energy than the 3p, which will be lower than the 3d. For the next set of orbitals,

in which n = 4, the 4s will be below the 4p, which will be below the 4d, which

will be below the 4f.

6.13 Electron Conﬁgurations

and the Aufbau Principle

Now that we have a complete set of orbitals and a general scheme for ranking

their energies, we can list all the orbitals occupied by the electrons of any atom

in the periodic table. The complete list of ﬁlled orbitals is called the

electron

conﬁguration

of an atom. We are often interested in the lowest energy conﬁgura-

tion, which represents the ground state of the atom. This can be generated by

adding one electron at a time to an unoccupied atomic orbital, starting with the

lowest energy orbital and working our way up in energies until all electrons in the

atom have been assigned an orbital. This method of ﬁlling hydrogen atomic or-

bitals to get multielectron conﬁgurations operates in accordance with the

Aufbau

principle

, from the German word for “building up.” The Aufbau principle says

that as protons are added to the nucleus, electrons are successively added to

orbitals of increasing energy, beginning with the lowest-energy orbitals. In

essence, we build up the electron conﬁguration one electron at a time until all

electrons are accommodated. To convey the maximum information in the mini-

mum space, we use a chemical shorthand to indicate which orbitals are occupied.

In its ground state, the hydrogen atom will have its lone electron in the 1s orbital,

H 1s

He 1s

Visualization: Orbital Energies

Tutorial: Aufbau Principle

FIGURE 6.40

The electron conﬁguration of the ﬁrst

three elements of the second period.

FIGURE 6.41

hree possible electron conﬁgurations

for carbon.

246 Chapter 6 Quantum Chemistry: The Strange World of Atoms

this as 1s

. Moving on to helium, the next element in the periodic table, we place

the ﬁrst electron in the 1s orbital, but because we can have both up and down

spins associated with the spatial part of the orbital, the second electron will go

into a 1s orbital as well. Rather than writing out the spin state explicitly, we write

the electron conﬁguration as 1s

and just have to remember that the electrons in

this conﬁguration have opposite spins.

The next element in the sequence has three electrons. This element must be

lithium, which the periodic table places in the second row, below hydrogen and

helium. Lithium has been placed here because we have used up all the orbitals

with n = 1 and now must start another quantum level, or shell, by placing the

third electron in the 2s orbital. The ground-state electronic conﬁguration for

lithium is therefore 1s

. The other elements in the same row as lithium con-

tinue to ﬁll the second quantum shell:

Li: 1s

N: 1s

Be: 1s

O: 1s

B: 1s

F: 1s

C: 1s

Ne: 1s

In the above examples, note that the p orbitals ﬁll after a total of six electrons be-

cause 2p

,2p

, and 2p

can each accommodate two electrons, one with spin up

and one with spin down. Remember that the p orbitals are referred to as occupy-

ing their own subshell.

When we get to the end of the row, we will have completely ﬁlled another

shell. The next row must start ﬁlling the 3s orbitals because there is no more room

for electrons in the n = 2 shell. Now you can begin to understand how the struc-

ture of the periodic table shows a splendid consistency, whether we are classifying

elements in terms of physical and chemical properties, as did Mendeleev and Meyer,

or by the quantum mechanical solution to the Schrödinger equation in the order of

increasing electron energy, as did the quantum chemists and physicists.

In order to proceed to the next row, or period, of the periodic table, we

still need to know a few more things about how electrons ﬁll the orbitals. Be-

cause of their negative charge, electrons tend to remain as far apart as possi-

ble in a manner that minimizes repulsive interactions among them. When

ﬁlling the 2p orbitals for boron through neon, we could keep the electrons far-

ther apart on the average by placing them into different 2p orbitals for as long

as possible. We could also minimize the repulsive electron–electron interac-

tions by keeping the spins of the electrons parallel—that is, with their re-

spective spin axes pointing along the same direction. To illustrate this, we will

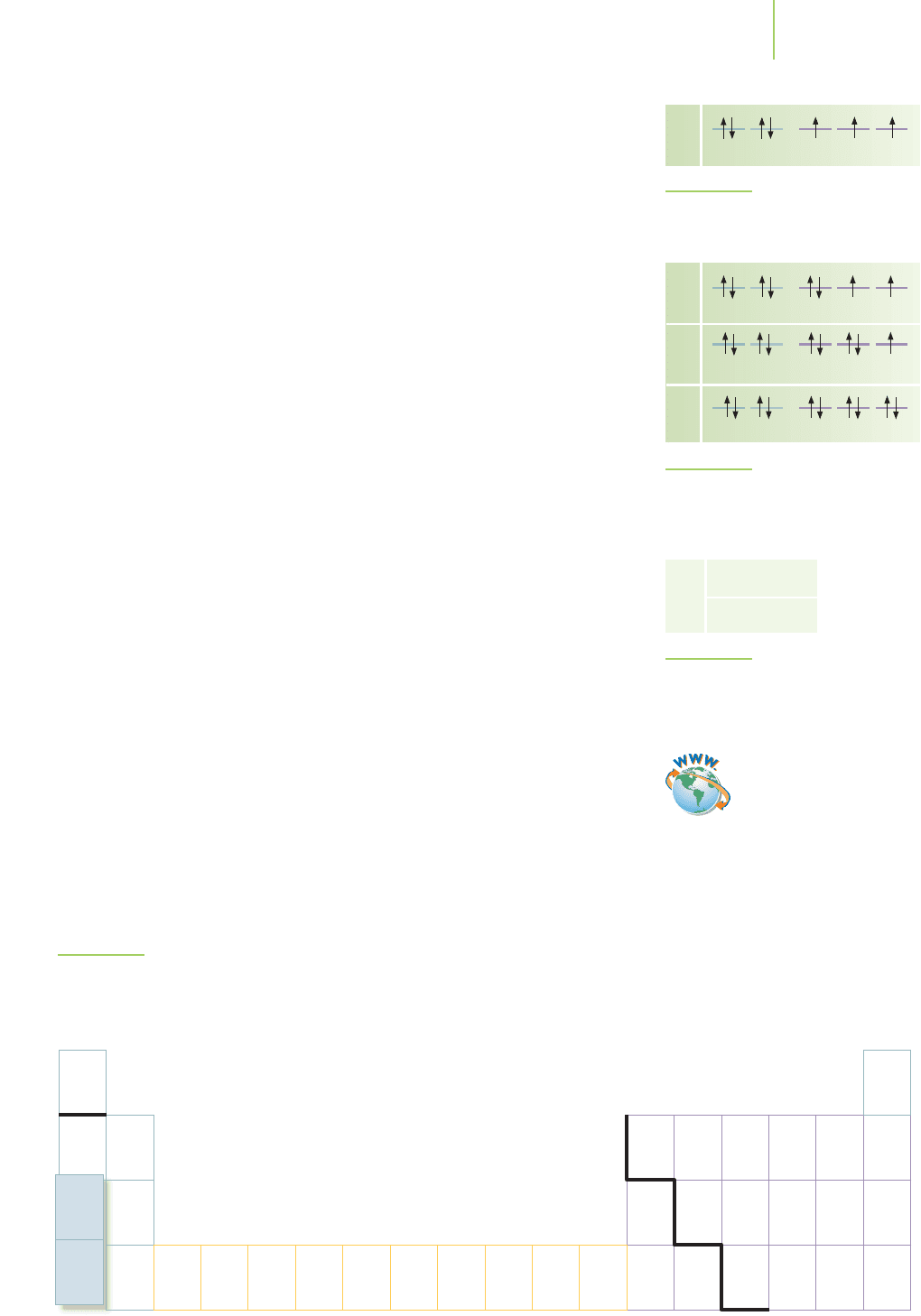
ﬁll the electrons from the second period of the chart one more time. The ﬁrst

three, shown in Figure 6.40, are unambiguous.

For boron, the 2p

orbital choice is arbitrary. Either the 2p

or the 2p

orbital would have been equally valid. To extend the series to carbon, we now

have to decide whether we will place the two 2p electrons in the same orbital

or in different orbitals. Three unique choices are possible, as shown in

Figure 6.41, all of which represent possible electronic states for the carbon

atom.

The ground state for the carbon atom is state 1, which has the two 2p elec-

trons in different orbitals with the spins aligned in the same direction. It is the

lowest energy state for carbon, and it is therefore the state in which you will

ﬁnd a carbon atom unless you supply it with energy—by irradiating it with

electromagnetic radiation, for example.

To understand why we need to keep spins aligned the same for partially

ﬁlled levels, remember that no two electrons in an atom can have the same

four quantum numbers n, l, m

, and m

(Pauli exclusion principle). Giving the

two 2p electrons the same spin gives them the same value of m

and requires

that they be placed in different 2p orbitals. This keeps the two electrons

H 1s

Ne 1s

=1s

1s 2s 2p

State 1:

State 2:

1s 2s 2p

State 3:

Video Lesson: Electron

Conﬁgurations through Neon

6.13 Electron Conﬁgurations and the Aufbau Principle 247

spatially separated and therefore minimizes the repulsion between the two. Over-

all, this behavior is summarized by what is known as

Hund’s rule. Proposed by the

German physicist Friedrich Hund in 1925, this rule states that when orbitals of

equal energy are available, the lowest energy conﬁguration for an atom has the

maximum number of unpaired electrons with parallel spins.

If we continue adding the electrons to the hydrogen-like atomic orbitals, we

will have the maximum number of unpaired 2p electrons for nitrogen, as shown

in Figure 6.42.

We must again begin pairing them to continue adding electrons to the or-

bitals, as shown in Figure 6.43. By the time we get to neon, the entire second shell

is ﬁlled.

To proceed to sodium, we need to add the next electron to the 3s level. Even

with our shorthand notation, the electron conﬁgurations are beginning to get

unwieldy. However, we can say that all atoms in the third row of the periodic table

must have ﬁlled the n = 1 and n = 2 shells before electrons can be added to the

n =3 level. This allows us to write the electron conﬁguration in one of two ways,

as given in the example for sodium as shown in Figure 6.44. The ﬁrst notation

shows all of the electrons explicitly, and the second uses [Ne] to take the place of

. We can say that the conﬁguration of sodium is 3s

with a neon core.

The electrons listed after the

core electrons ([Ne]) are called valence electrons and

will be very important in establishing the chemical reactivity of the element.

Similarly, the ground-state electron conﬁguration for potassium could be

written either explicitly as 1s

or as [Ar]4s

. The latter case indi-

cates only the electrons in the outermost shell of the conﬁguration and places the

less reactive, more strongly bound ﬁlled-shell electrons into an argon core. This

does not imply that the nucleus of potassium has been replaced with argon.

Argon has one fewer proton and, for the most abundant of their isotopes, two

more neutrons than does potassium. The [Ar] core notation signiﬁes that the

atomic conﬁguration has the same hydrogen-like orbitals occupied with elec-

trons plus all the others noted after it.

You might have noticed that the argon ground-state electron conﬁguration

has been given as 1s

but that when we added one more electron to

the set to represent the occupied orbitals of potassium, the next element in the

periodic table, we placed it into a 4s level. This makes sense from the position that

potassium occupies in the periodic table: right under sodium, as shown in

Figure 6.45. And rubidium, which is directly under potassium, has the electron

conﬁguration of [Kr]5s

. In fact, all the elements in the ﬁrst column of the

1s 2s 2p

FIGURE 6.42

The electron conﬁguration for nitrogen.

1s 2s 2p

FIGURE 6.43

The electron conﬁguration for the last

three elements of the second period.

[Ne]3s

FIGURE 6.44

The electron conﬁguration

for sodium can be

written two ways.

IIA

IIIA

IVA

VIA

VIIA

VIIIA

13 14 15 16 17

8 9 10 11 1234567

FIGURE 6.45

Position of potassium and sodium on the periodic table.

Video Lesson: Electron

Conﬁgurations Beyond Neon