Kelter P., Mosher M., Scott A. Chemistry. The Practical Science

Подождите немного. Документ загружается.

228 Chapter 6 Quantum Chemistry: The Strange World of Atoms

Going to the three dimensions required to quantize the spatial position of

electrons in the Bohr hydrogen atom is considerably more difﬁcult. Bohr himself

never actually assigned a wavelength to his electrons, which remained decidedly

particle-like in his own model. Bohr merely postulated that the momentum and

radius of permissible levels were quantized because they had to be if his model

were to explain the hydrogen emission spectrum. But the reason why space and

energy are quantized for the hydrogen atom arises from the wave-like nature of

the electron.

If electrons behave like waves, how do we ﬁnd their wavelengths? We can do

this by using the de Broglie formula, proposed by Louis de Broglie in 1924:

λ =

The equation, which shows that the wavelength, λ, is inversely proportional to

the momentum, p, through Planck’s constant h, connects wave (λ) and particle

(p = momentum) properties in a single formula. Again, note that the momen-

tum term, p, uses the velocity (v). This symbol looks similar to that for the fre-

quency (ν), but it is vastly different. The velocity has units of m/s, whereas

frequency has units of 1/s.

What is the purpose of the de Broglie equation? It illustrates the basic principle

of the wave–particle duality: Moving particles exhibit deﬁnite wave-like character-

istics. The values of wavelengths calculated by this equation are meaningful for

small, fast-moving particles such as the electron. The calculation is less meaning-

ful but still demonstrative for massive, slow-moving objects.

EXERCISE 6.5 Working with the de Broglie Equation

An electron in the ground state of the hydrogen atom has a velocity of about

2.1 × 10

−1

. What is its de Broglie wavelength?

Solution

λ =

6.626 ×10

−34

J·s

(9.109 ×10

−31

kg) × (2.1 ×10

m·s

−1

)

n = 1

n = 2

n = 3

n = 4

n = 5

Orbit n Distance from Nucleus

0.529 A

2.116 A

4.761 A

8.464 A

13.225 A

(a)

(b)

FIGURE 6.16

The requirements of a wave completing a circular path.

This wavelength doesn’t line up as the circular orbit is

completed (b). This doesn’t provide a suitable orbital. In (a),

the wavelength does line up and provides a useful orbital.

FIGURE 6.15

Circular cross-sections

of the atomic energy

levels of the

Bohr atom.

Louis-Victor de Broglie (1892–1987),

a French physicist and prince, published

his wave–particle duality theory in 1924.

Video Lesson: The Wave Nature

of Matter

6.7 The Heisenberg Uncertainty Principle 229

Because 1 J = 1 kg

−2

, substituting yields

6.626 ×10

−34

kg·m

·s

−2

(s)

(9.109 ×10

−31

kg) × (2.1 ×10

m·s

−1

)

= 3.5 ×10

−10

m = 3.5Å,or0.35 nm

PRACTICE 6.5

Calculate the de Broglie wavelength for a 1200-lb car traveling 75 mi/h.

See Problems 59 and 60.

One application of the wave nature of electrons lies in their very small wave-

length. Microscopes magnify and allow us to see objects with visible light. The

limit to their magniﬁcation is the wavelengths of electromagnetic radiation (in

this case, visible light). Objects must be larger than the wavelengths of the radia-

tion in order to be seen. Using an optical microscope, we are able to see objects as

small as about 200 nm (the radius of a hydrogen atom is 25 picometers, or

0.025 nm). We are able to see objects much smaller than this if we use electrons

to image the objects. This is the principle behind the scanning electron micro-

scope (SEM). Scanning electron microscopes operate much like compound light

microscopes, but they use a beam of electrons to generate an image of the sample

rather than using light to image the sample. Because the wavelength of an elec-

tron is about 1000 times smaller than that of visible light, and given instrumental

imperfections, a scanning electron microscope can image objects or features as

small as about 3 nm. This means that the SEM can achieve a magniﬁcation of up

to 300,000-fold. Unfortunately, this is still too large to “see” individual atoms. For

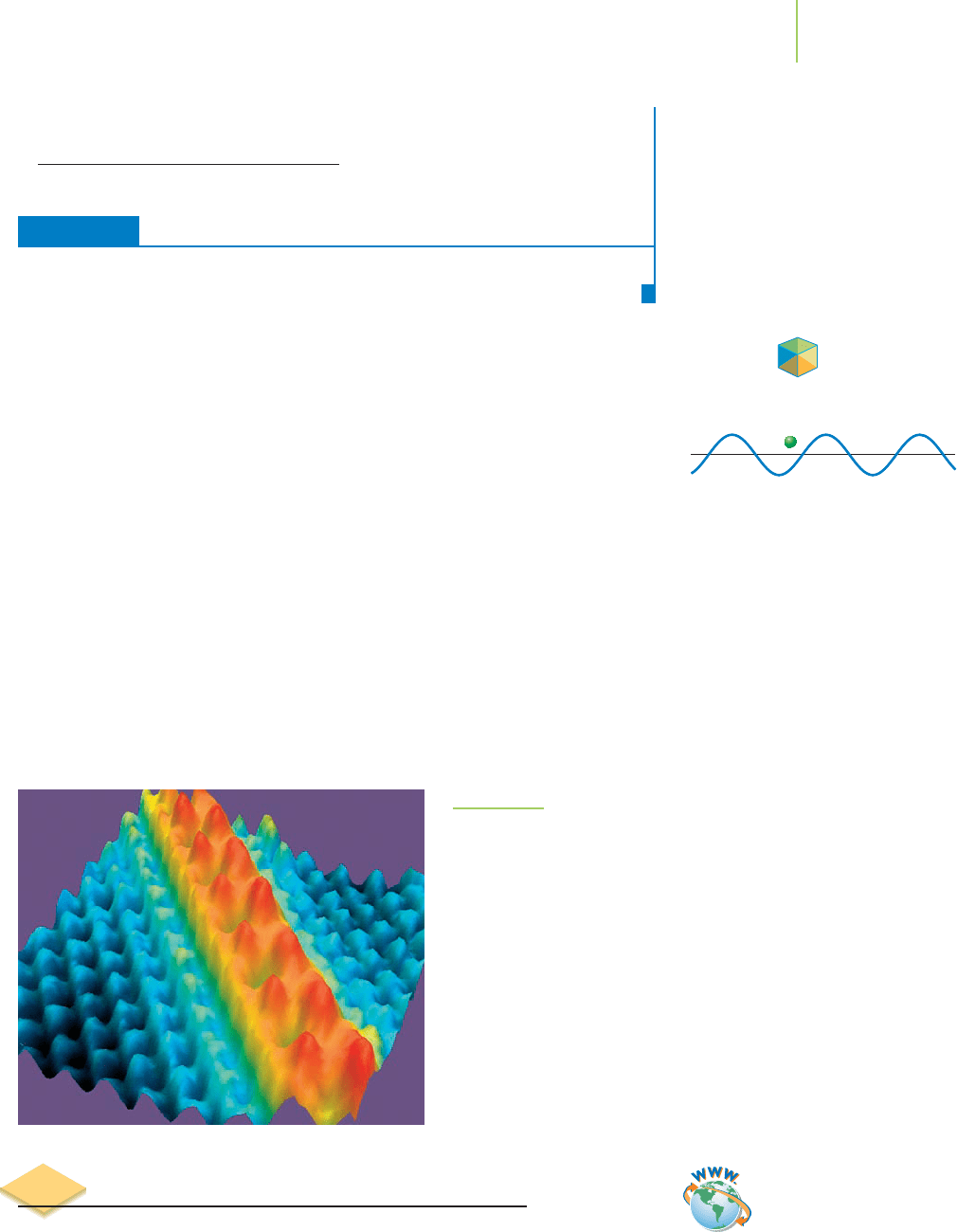
that we need to use a scanning tunneling microscope (STM) (see Figure 6.17).

The STM takes advantage of another quantum effect, tunneling, which we will

discuss in Section 6.10.

Application

An atom is smaller than the visible

wavelengths of light and cannot be seen

with an optical microscope.

FIGURE 6.17

Scanning tunneling microscope

image of cesium atoms lined

up in zigzag fashion on a GaAs

surface. An STM can allow us

to “see” objects at a much

higher magniﬁcation than an

optical microscope.

6.7 The Heisenberg Uncertainty Principle

How does wave–particle duality alter our ideas of how the electron is moving within

the hydrogen atom?

The Bohr model regards the electron as a particle allowed to

orbit the nucleus at only certain precisely quantized distances. However, if it is

also to behave as a wave, the electron must be spread out over all of its orbit in the

hydrogen atom. We can reconcile these two very different ideas by considering

scale. Assume that we measure the electron’s position as having a speciﬁc value of

x, y, and z in our macroscopic laboratory setting. If the electron is bound in a

Video Lesson: The Heisenberg

Uncertainty Principle

230 Chapter 6 Quantum Chemistry: The Strange World of Atoms

The position and momentum of a racing

car are known with enough precision for

the macroworld.

hydrogen atom but is somehow spread out, some uncertainty will be introduced

into our measurement of x, y, and z. But the uncertainty is very small, on the

order of 0.1 nm or so. Our macroscopic rulers are not this precise, so it looks to

us as if the electron is at a speciﬁc and absolute position in space.

If we then look at the electron on the microscopic level, we ﬁnd that the best

we can do to establish its position is to say it is somewhere in the atom, within a

certain range from of the atom’s center. We see a particle’s behavior of spatially

discrete positions with continuous possible values when we are looking at things

on a macroscopic scale, and we see a wave’s behavior of being allowed only in spe-

ciﬁc regions of space but spread out to ﬁll the “container” of the atom when we

make microscopic measurements.

This leads us to another of the “Funny things happen” phenomena that we

observe only when we are in the microscopic quantum world. On a macroscopic

level, you can measure both the position and the momentum of a particle as pre-

cisely as your instruments will allow. Quantum mechanics, however, proposes

that, regardless of the instrument used to measure them, there is an ultimate un-

certainty in both the position and the momentum of a particle, and these uncer-

tainties are connected. This is called the

Heisenberg uncertainty principle after

Werner Heisenberg, who proposed it in 1925. Mathematically, we can state the

Heisenberg uncertainty principle as

xp

≥

4π

where ∆x is the uncertainty in position, ∆p

is the uncertainty in momentum

along the x-direction, and h is Planck’s constant.

There is no limitation on how precisely we measure either x or p

. Instead, the

limitation is on the product of their uncertainties ∆x∆p

. In other words, as the

uncertainty in x becomes smaller, the uncertainty in p

gets larger. Therefore, as

∆x approaches zero and we know exactly where the particle is positioned, ∆p

be-

comes inﬁnite and we do not know anything of its momentum. In essence, it can

have any value of momentum possible, including inﬁnity. If we know the mass of

the particle, then inﬁnite momentum implies inﬁnite velocity. In short, limita-

tions are set on real-world behavior by the Heisenberg uncertainty principle,

which among other things limits the maximum achievable resolution of micro-

scopes, the ultimate size of computer chips, and, in the nanoworld, the behavior

of actual atoms and molecules.

6.8 More About the Photon—

the de Broglie and Heisenberg Discussions

We have focused on the electron in our previous discussion, but the principles

apply to all particles, although the effect will really be evident only on the micro-

scopic level. Any small particle such as the electron, proton, or neutron would be

a good candidate for testing the Heisenberg uncertainty principle. Bowling balls,

elephants, and cars would not. But what about phenomena that are wave-like in

our macroscopic world? What happens to waves on the quantum scale?

Electromagnetic radiation is wave-like on a macroscopic level. Light, in a

manner similar to chemical substances, can be decreased only so far. Eventually,

you will come to its smallest, indivisible unit. For light, the smallest unit is the

photon, and, like particles, photons have been shown to carry momentum,

another of our particle-like characteristics. In fact, we can calculate the momen-

tum using the de Broglie equation.

What does such a calculation tell us? Photons,

although we think of them primarily as waves, act like particles too. Again, the

calculation veriﬁes the particle–wave duality.

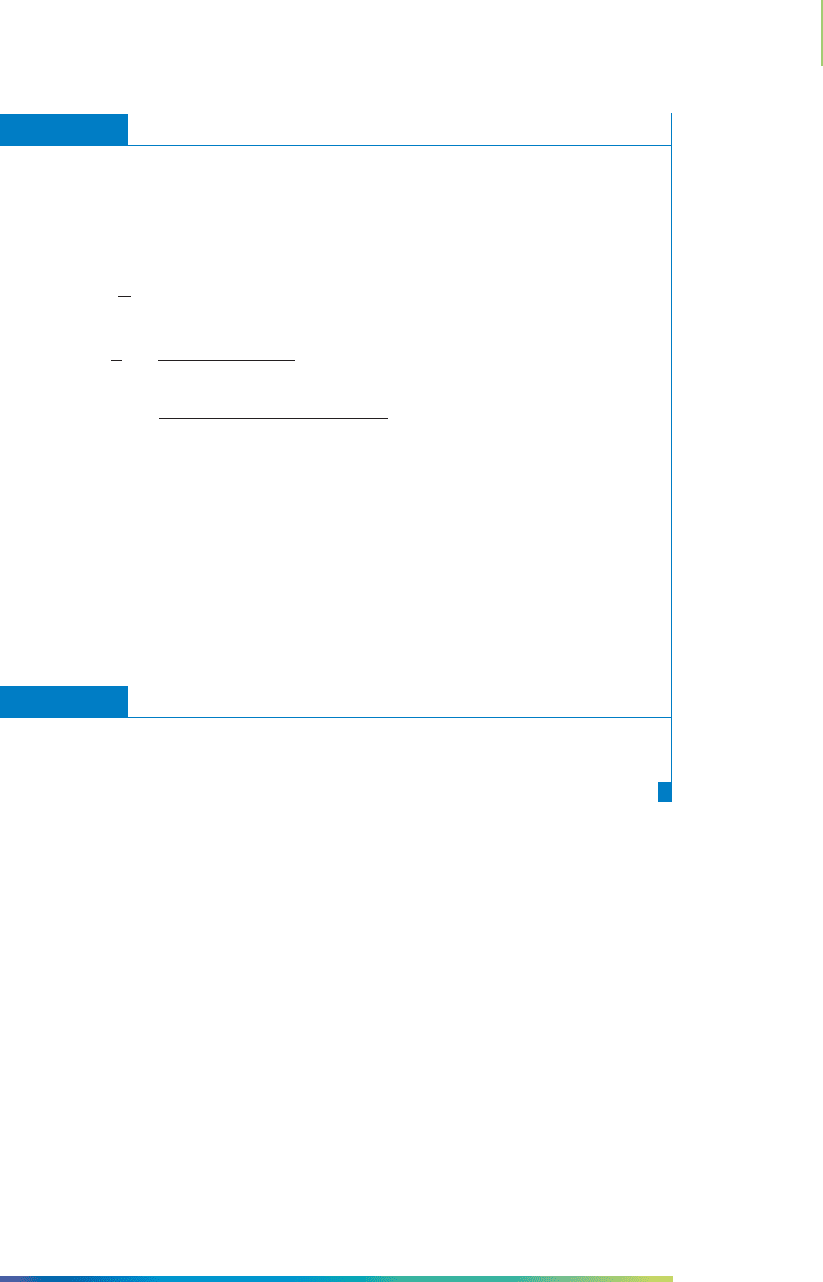
6.8 More About the Photon—the de Broglie and Heisenberg Discussions 231

EXERCISE 6.6 Photons and Momentum

How much momentum is carried by a single green photon and by a mole of green

photons? Assume that green photons have wavelengths of 530 nm.

Solution

We can use the de Broglie equation to calculate the momentum of a single photon.

Because

λ =

p =

6.626 ×10

−34

J·s

5.30 ×10

−7

6.626 ×10

−34

kg·m

·s

−2

× s

5.30 ×10

−7

= 1.25 × 10

−27

kg·m·s

−1

This is for a single photon. If we want the momentum for a mole of photons, we

must multiply this value by Avogadro’s number:

p = 1.25 × 10

−27

kg·m·s

−1

photon

−1

× (6.022 × 10

photons

mol

−1

)

= 7.53 × 10

−4

kg·m·s

−1

·mol

−1

Does our answer make sense? In comparison, a 68-kg (150-lb) person ambling

down the road at 2 mi/h has a momentum of 60

kg·m·s

−1

, so you can see that even

a mole of green photons has a much smaller momentum.

PRACTICE 6.6

Calculate the momentum of a mole of photons with a wavelength of 200 nm, of

700 nm, and of 1000 nm. Is there a difference? Explain.

See Problems 65–70.

A word of caution about this type of calculation: The wavelength will have the

same value, as will the frequency, whether you have one photon or a mole of pho-

tons. These properties of a photon are intrinsic properties—they do not change

with a change in amount. The total momentum and energy carried by the elec-

tromagnetic radiation, however, are extrinsic properties because both depend on

the number of photons you have.When we use the formula E = h

, we always use

the energy of a single photon. Similarly, with the de Broglie equation, we always

use the momentum of a single photon.

We also need to be careful of the answer that the de Broglie equation gives us

for the mass of a photon. The mass that appears in the de Broglie formula is

known as the

rest mass, the mass the particle would have if it were not moving at

all. Photons, however, are moving at 2.998 × 10

m/s, and slowing them down to

zero speed is just not feasible. The rest mass you calculate for photons from the de

Broglie formula does not make any sense for a photon at the speed of light. Blame

this discrepancy on Einstein’s relativistic effect, if you like.

HERE’S WHAT WE KNOW SO FAR

■

Small particles behave both as waves and as particles.

■

Photons have both wave and particle characteristics.

■

The de Broglie equation illustrates the relationship between wave and particle

characteristics.

■

The Heisenberg uncertainty principle further veriﬁes that small particles have

wave-like characteristics.

232 Chapter 6 Quantum Chemistry: The Strange World of Atoms

Erwin Schrödinger (1887–1961)

was awarded the 1933 Nobel Prize

in physics for his development of

the theory we use to describe the

structure of an atom.

6.9 The Mathematical Language

of Quantum Chemistry

The language of quantum chemistry is mathematics. In quantum chemistry,

knowing a few of the more important relevant mathematical concepts will pave

the way for us to explore the current understanding of atomic structure, which

has developed far beyond the Bohr model. The heart of our current understand-

ing of the atom lies within a simple-looking mathematical equation:

H

= E



This is the time-independent Schrödinger equation. This equation allows us to

calculate the exact energies, E

, available to the electrons in an atom, if we know

the mathematical description,



, called the wave function, that describes the

positions and paths of the electron in its given energy level (n). Although it appears

harmless, the wave function,



, is a complex equation containing variables, con-

stants, and quantum numbers. This function tells us everything we can possibly

know about our system from a quantum mechanical perspective. It is called a

wave function because it is derived from equations developed to predict

the properties of waves. The

in the Schrödinger equation is known as the

Hamiltonian operator after William Hamilton (1805–1865), an Irish mathemati-

cian who early on did work that hinted at wave–particle duality (Figure 6.18). In

simple terms, an operator is a mathematical term, such as +, −,

∗

, ⁄, or (in this

case)

, that tells us how to proceed—what operation to do—in a mathematical

equation. The Hamiltonian is one of the more complex operators that we’ll en-

counter; it is too complex for us to carry out, in this discussion, the operation it

calls for. However, the conclusions that result from the operation are fundamental to

our proper view of atomic structure.

To illustrate the implications and utility of the Schrödinger equation, let’s ex-

amine the values of a wave function, shown in Figure 6.19, for a particle con-

strained to move in only one dimension.

FIGURE 6.18

William Hamilton (1805–1865), devel-

oper of the Hamiltonian operator.

Wave function

Energy

Probability density

8.35  10

–22

33.38  10

–22

75.11  10

–22

133.54  10

–22

208.65  10

–22

n = 1

n = 2

n = 3

n = 4

n = 5

FIGURE 6.19

The wave functions, energy levels, and

probability functions for a particle con-

ﬁned to a one-dimensional box. The par-

ticle is deﬁned by a wave function that

has nodes at each end of the wave, indi-

cating that the particle cannot be found

at the wall or outside the box.

6.9 The Mathematical Language of Quantum Chemistry 233

In this example, our particle can move between two points within that one

dimension. Think of this as a one-dimensional container or box that will conﬁne

a particle. If we use the Schrödinger equation and solve for the energy of the par-

ticle, we ﬁnd the ﬁrst three wave functions shown starting from the bottom of the

box in Figure 6.19. These are called standing waves, which oscillate in time just

like the string on a violin, and we show them as a snapshot in time at their great-

est amplitude. The ﬁrst level is described by half the wavelength of a sine wave.

The second level is described by a full sine wave and has a

node in the center of the

wave function—a point in the wave function where the amplitude is always zero.

The next level, represented by one and a half sine wavelengths, has two nodes that

divide the wave function into three segments. The wave function with n = 4

would have an additional node for a total of three, and the wave function n = 5

would have still another for a total of four.

Additionally, complex calculations of a particle in a one-dimensional box

result in an equation illustrating the permitted energy levels for this model:

8 mL

where n is the quantum level (n =1, 2, 3, . . .), h is Planck’s constant, m is the mass

of the particle, and L is the length of the box. Although the one-dimensional

model that gave rise to this equation is simple (it is based on a box containing a

particle), it explains the intense colors observed in leaves and ﬂowers as well as

other materials. Certain molecules within a ﬂower petal contain delocalized

electrons (electrons that are able to move across a molecule; we’ll have much more

to say about this in Chapter 9). The molecule itself acts as a one-dimensional

“box” because of its bonding structure. When a photon is absorbed by one of

these electrons, it becomes excited and moves to a higher energy level described by

our simple one-dimensional model. The energy differences between the lower

energy level and the excited energy level correspond to the color we observe. The

length of the bond or bonding structure deﬁnes the length of the box, L in the above

equation.

If we calculate the energy of an electron conﬁned to a box the size of a single

covalent bond (1.5 × 10

−10

m), the wavelength of the energy needed to excite the

electron corresponds to ultraviolet light. If several atoms deﬁne the “box,” as is

seen in some types of molecules common within ﬂower petals, then the energy

is smaller (because L is bigger), and the electrons can absorb visible light. For

example, cyanidin-based compounds, shown in Figure 6.20, are responsible for

the red color of apples, autumn leaves, roses, strawberries, and cranberry juice.

Changing the structure of the molecule changes the size of the box, which

changes the color of the photons absorbed.

Introducing Orbitals

One of the more interesting outcomes of the Schrödinger equation is that we can

use the wave function to reveal where an electron is most likely to be found within

an atom. We say“most likely”because we can never pin the electron down exactly,

as the Heisenberg uncertainty principle tells us. Instead, we can only determine

the probability of ﬁnding it at each point in space. The space that the electron is

allowed to occupy in a given energy level on an atom is called an

orbital.

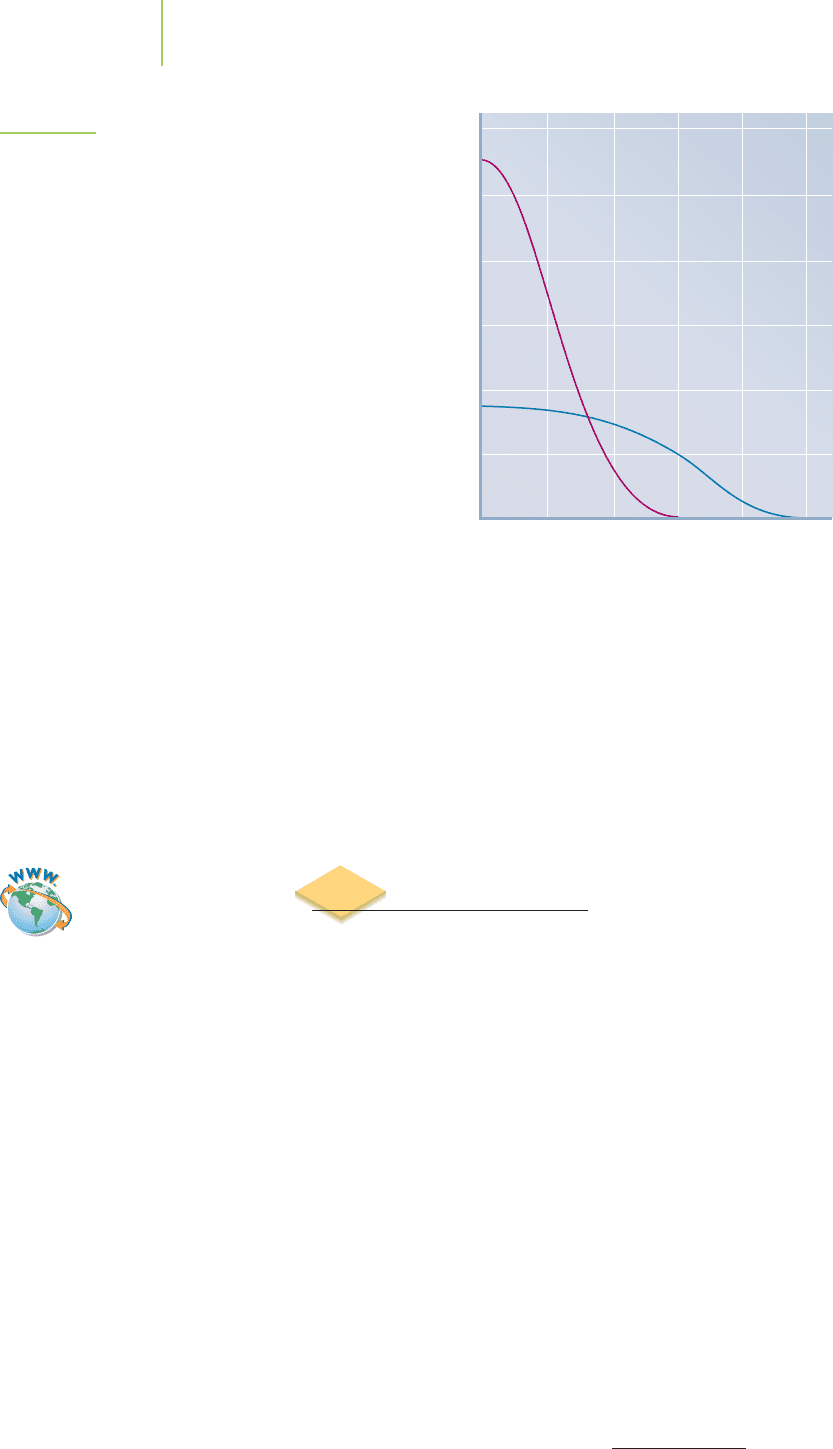
For example, if we plot the wave function of an electron around a nucleus, we

get a ﬁgure similar to that shown in Figure 6.21. We can mathematically manip-

ulate the wave function to create a new function depicted as 

∗

, which looks a

lot like the square of the wave function . The great usefulness of 

∗

 is that it

is proportional to the probability of ﬁnding the particle at a particular point in space.

The nodes in  remain at the same places in 

∗

, but all values of 

∗

 are pos-

itive. In short, the probability function describes the spatial distribution of the elec-

tron around an atom; 

∗

 describes the shape of an orbital.

Cyanidin

FIGURE 6.20

This molecule is responsible for many of

the colors found in plants.

The colors we see in a ﬂower are due to

the molecules that are present in the

petals. These molecules can be thought

of as examples of the one-dimensional

particle in a box.

234 Chapter 6 Quantum Chemistry: The Strange World of Atoms

12345

0.4

0.6

0.3

0.2

0.1

0.5

Radial distance

Wave function value

FIGURE 6.21

A plot of the wave function (blue line) represented as the

distance from the nucleus. The probability function (*;

red line) represents the most likely shape of the orbital re-

sulting from the wave function.

The idea that a single particle, like an electron, doesn’t exist at a single point

in space, but is merely more likely to be found at certain places and less likely to

be found at others, is admittedly rather odd. But it ﬁts the ideas presented here

and years of measurements that conﬁrm these ideas. Note that there are nodes

where we can guarantee that the particle will never be found. At these nodes, the

probability function, 

∗

, is equal to zero. An electron can never be found at a

node. The electron can be found on either side of the node, but never at the node.

How does it go from one side to the other, if it is never allowed to be on the node?

It does this by behaving like a wave, which has amplitude on both sides of the

node: a clear demonstration of wave–particle duality.

6.10 Atomic Orbitals

Both the Hamiltonian operator and the wave functions for the hydrogen atom

are known, and they allow us to develop both mathematical and visual represen-

tations of the orbitals that electrons can occupy in the three-dimensional space

around the hydrogen nucleus. Specialists in quantum chemistry describe this

three-dimensional system in terms of a radial part and an angular part.

Radial

means “along the radius” and angular means “as a function of the angles that

describe the orientation of the radius.” Because the calculations of these three-

dimensional orbitals are quite complicated, we present only the results here. We

will use these results to explain, over the next several chapters (and, from time to

time, for the remainder of the textbook), how and why atoms and molecules

interact the way they do.

Quantum Numbers and s Orbitals

There are four different quantum numbers in the wave function for the electron in

the hydrogen atom, and they are given the symbols n, l, m

, and m

. The n is

known as the

principal quantum number and can be any whole number n = 1, 2,

3,...,∞. We are already familiar with the principal quantum number. This n is

what Bohr referred to as the energy levels in his atom. Based on the possible

values of n, there are an inﬁnite number of energy levels for the hydrogen atom.

The energy of each is given by

=−

2.1786 ×10

−18

Video Lesson: Atomic Orbital

Size

6.10 Atomic Orbitals 235

which is just what was predicted by the Bohr model. In atoms with more than one

electron, any electrons with the same value for the principal quantum number

(n) are said to occupy the same

principal shell, but only the energy levels in the

hydrogen atom are given by this equation.

Two of the other three quantum numbers, l and m

, depend on the value of n.

The

angular momentum quantum number, l, can be any number from zero to n − 1

in whole-number steps:

l = 0,1,2,...,n − 1

This quantum number is considered to represent the shape of the electron orbital.

In the ﬁrst energy level, n = 1, the equation used to calculate the angular mo-

mentum quantum number reveals that l =0. This implies that only one shape of

orbital is possible in the ﬁrst energy level. In the second energy level, n = 2, the

value of l can be 0 or 1. This means that there are two different shapes of the

orbitals in the second energy level. When n =3, l can be 0, 1, or 2 (three different

shapes). And so on, all the way to inﬁnity. Any electrons that share the same

values for n and l are said to occupy the same

electron subshell.

The m

quantum number is the magnetic quantum number (also known as the

orbital angular momentum quantum number). It is based on the value of l and

can have any value from l to −l in whole numbers.

=−l,...,−2, −1,0,1,2,...,l

This quantum number can be thought of as deﬁning the direction in which the

individual electron orbitals are pointed. For example, a speciﬁc orbital could be

oriented along the x axis or the y axis. The value of m

indicates this direction.

The number of possible values for the magnetic quantum number indicates

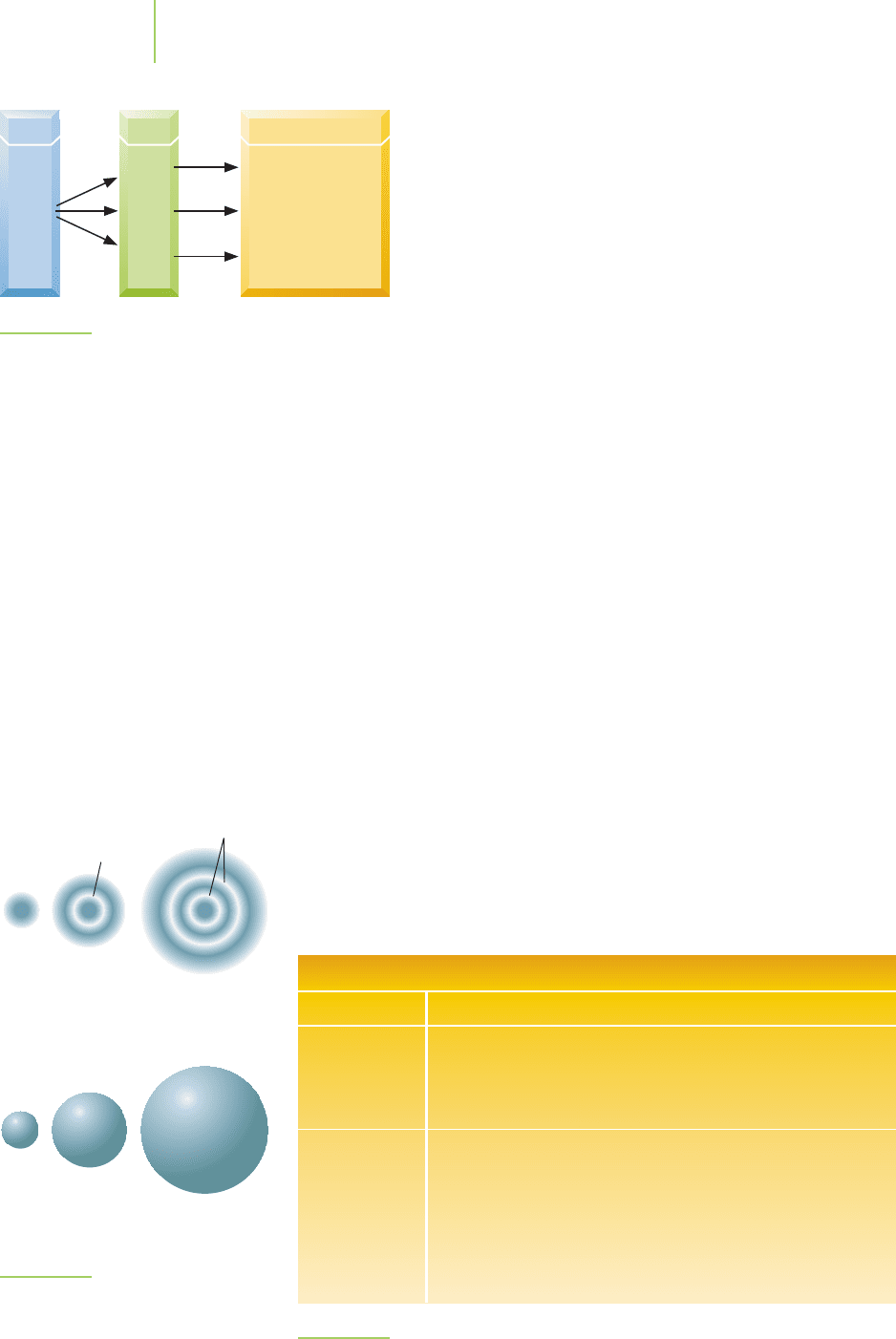
the number of speciﬁc orbitals of a speciﬁed shape, as illustrated in Figure 6.22.

For example, in the second principal shell, when n = 2, we determined that there

are two values for l, l = 0 and l = 1. We need to consider each of these values to

generate all the possible sets of quantum numbers. When n =2 and l =0, m

can

only be 0 (one orbital). When n =2 and l =1, m

can be −1, 0, or +1. In this case,

we have three speciﬁc orbitals of the same shape oriented in three different direc-

tions. Calculating all of the possible orbitals within an energy level can be a

1, 0 –1

1, 0, –1

2, 1, 0, –1, –2

1, 0, –1

2, 1, 0, –1, –2

3, 2, 1, 0, –1, –2, –3

Subshell

notation

Number of

orbitals in the

subshell

Number of

electrons needed

to fill subshell

Maximum possible

number of electrons

in shell

FIGURE 6.22

Allowed values for n, l,

, and m

quantum num-

bers for hydrogen atomic

orbitals.

Video Lesson:

Atomic Orbital

Shapes and

Quantum

Numbers

(n, l, m

, m

)

Energy Level 1:

Energy Level 2:

Energy Level 3:

(1, 0, 0, + ); (1, 0, 0, – )

(2, 0, 0, + ); (2, 0, 0, – )

(2, 1, 1, + ); (2, 1, 0, + ); (2, 1, –1, + )

(2, 1, 1, – ); (2, 1, 0, – ); (2, 1, –1, – )

(3, 0, 0, + ); (3, 0, 0, – )

(3, 1, 1, + ); (3, 1, 0, + ); (3, 1, –1, + )

(3, 1, 1, – ); (3, 1, 0, – ); (3, 1, –1, – )

(3, 2, 2, + ); (3, 2, 1, + ); (3, 2, 0, + ); (3, 2, –1, + ); (3, 2, –2, + )

(3, 2, 2, – ); (3, 2, 1, – ); (3, 2, 0, – ); (3, 2, –1, – ); (3, 2, –2, – )

–

FIGURE 6.24

Systematic bookkeeping for quantum numbers.

236 Chapter 6 Quantum Chemistry: The Strange World of Atoms

daunting task because the number of orbitals gets large fairly

quickly, as shown in Figure 6.23. But as long as you are systematic

about what is essentially a bookkeeping task, confusion can be

kept to a minimum.

The ﬁnal quantum number, m

, is known as the electron spin

quantum number

(it is also known as the spin angular momentum

quantum number). Fortunately for our bookkeeping, the only

possible values for m

are +

and −

. The value of m

can be

either +

or −

for every set of n, l, and m

allowed.

We can use shorthand to indicate the four quantum numbers

that describe the position of electrons in an atom using the nota-

tion (n, l, m

). As shown in Figure 6.24, for n = 1 the sets of quantum num-

bers for the electrons are (1, 0, 0,

) and (1, 0, 0, −

). For n = 2 the sets are (2,

1, 1,

), (2, 1, 1, −

), (2, 1, 0,

), (2, 1, 0, −

), (2, 1, −1,

), (2, 1, −1, −

(2, 0, 0,

), and (2, 0, 0, −

). If you try n = 3, you should get 18 sets of quantum

numbers, and for n =4 you should get 32. Note how this follows a general trend.

The number of possible quantum numbers in each energy level is 2n

How do these values help us model the electronic structure of atoms? Although

the speciﬁc set of four quantum numbers represents a convenient label for a spe-

ciﬁc hydrogen atomic wave function, quantum numbers are much more than

that. The principal quantum number, n, gives the energy of the system and sets

the values of the l and m

quantum numbers. Together, the n, l, and m

tell us

about the spatial distribution of the electron and deﬁne the orbital shape and

size. For example, as shown in Figure 6.25, the radial component of the orbitals

with n = 1, 2, and 3 illustrates the difference in size of the atomic orbitals.

Orbitals that have equal energies are said to be

degenerate orbitals, and the

number of orbitals having the same energy is called the degeneracy. In the

hydrogen atom, orbitals with the same value of n and l have the same speciﬁc

amount of energy, and these orbitals are therefore degenerate. Consider the

orbitals within the second energy level (n =2). When n =2, l can be either 0 or 1.

When l = 0, the value of m

can be only 0. There is only one orbital, so it can’t be

degenerate. However, when l =1, m

can be −1, 0, or +1. In this case, three orbitals

with the same value for l are possible. These three orbitals have the same amount

of energy and are degenerate. The third energy level contains two sets of degener-

ate orbitals. One set contains three degenerate orbitals (l =1, m

=−1, 0, +1); the

other set contains ﬁve degenerate orbitals (l =2, m

=−2, −1, 0, +1, +2).

–1, 0, +1

–2, –1, 0, +1, +2

FIGURE 6.23

Outline of n, l, and m

values.

Nodes

Node

3s2s1s

(b)

3s2s1s

(a)

FIGURE 6.25

(a) The radial component of the probabil-

ity for the hydrogen atomic orbitals with

n =1, 2, and 3. (b) The spatial compo-

nent of those orbitals at 90% probability.

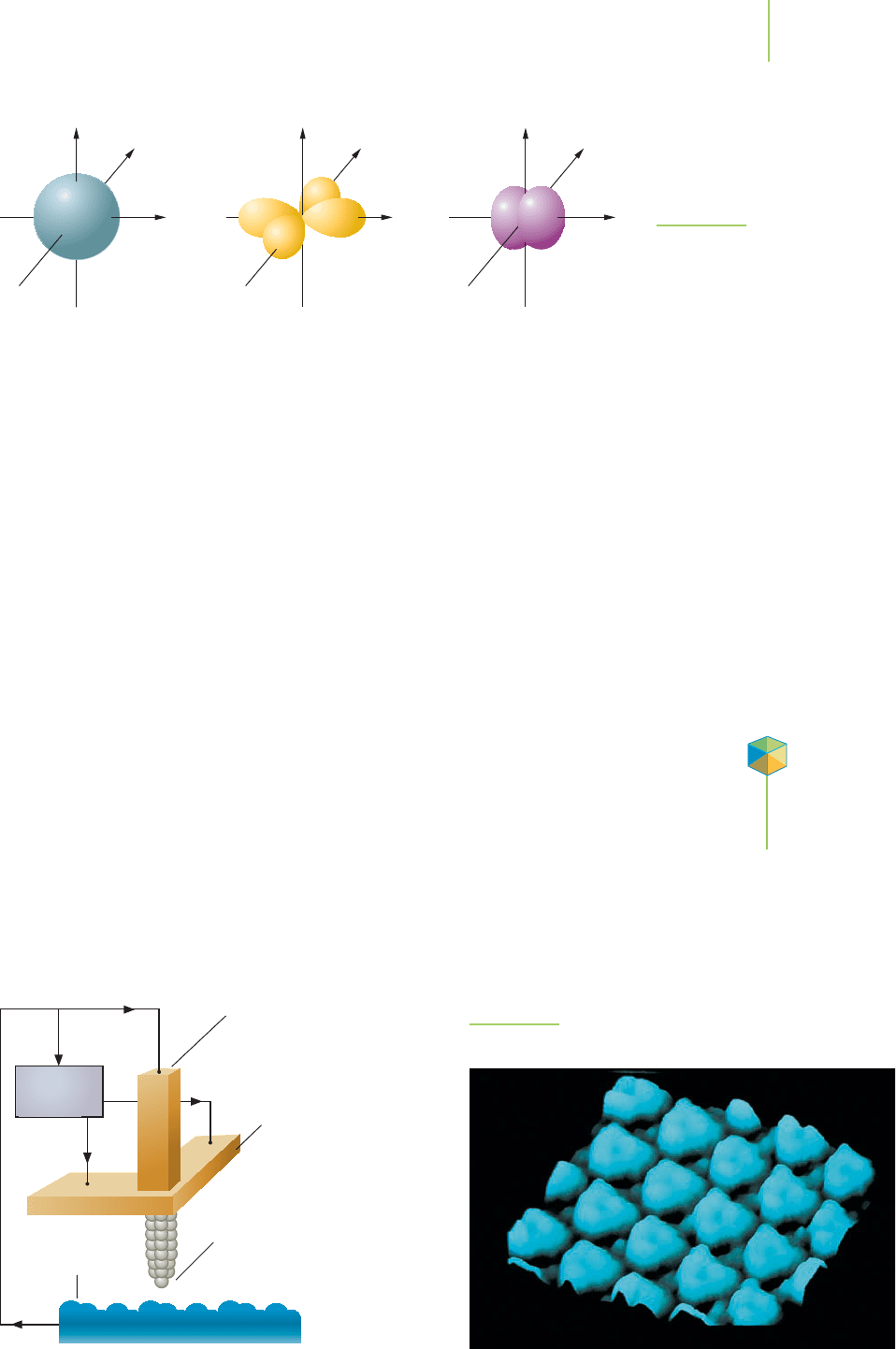
FIGURE 6.27

An STM tip scans over an object to produce an image.

6.10 Atomic Orbitals

237

Quantum chemists have been able to show us pictures that describe what the

quantum numbers tell us. For example, Figure 6.26 also shows us shapes of many

of the orbitals that we have described with quantum numbers. Remember that at

the atomic level, we can no longer speak in terms of absolute locations but can

only give the probability of the quantum particle being in a given location. The

pictures therefore can show us only the most probable place to ﬁnd the electron

in the orbital. This means that if you were in Champaign, Illinois, studying a hy-

drogen atom in an atom trap, and you asked a friend to see whether he could ﬁnd

your atom’s electron in Perth, Scotland, there would be a ﬁnite probability (albeit

outrageously small) that he would be able to ﬁnd it there. We do not have instru-

ments that are sensitive enough to measure the tiny probability of an electron

existing in Scotland when its atom’s nucleus is in Illinois. To be honest, we would

be hard pressed to measure the probability even a few millionths of a millimeter

from the atom.

The Scanning Tunneling Microscope

The scanning tunneling microscope (STM) allows us to draw a picture that rep-

resents the surface of a material. This microscope is so powerful that it can even

“see” single molecules and atoms. The STM basically uses an atomic-sized needle

that runs across the surface of a material. As the tip moves, it runs up and over

molecules or atoms, and changes in the position of the tip of the needle are

recorded on a graph. It works because if we bring the tip of the needle close

enough to the sample material, the wave function of the atoms in the tip will

overlap with those of the sample. This allows electrons to move from the tip into

the material by a process called quantum tunneling. The electrons that “tunnel”

Application

HEMICAL ENCOUNTERS:

The Scanning

Tunneling

Microscope

Computer

Sample

surface

1 atom wide

tungsten probe

Rods move probe

across sample

Probe moves up and down

to maintain same distance

from sample

2s orbital 3d

–y

2 orbital 2p

orbital

FIGURE 6.26

Some atomic orbitals.