Kelter P., Mosher M., Scott A. Chemistry. The Practical Science

Подождите немного. Документ загружается.

168

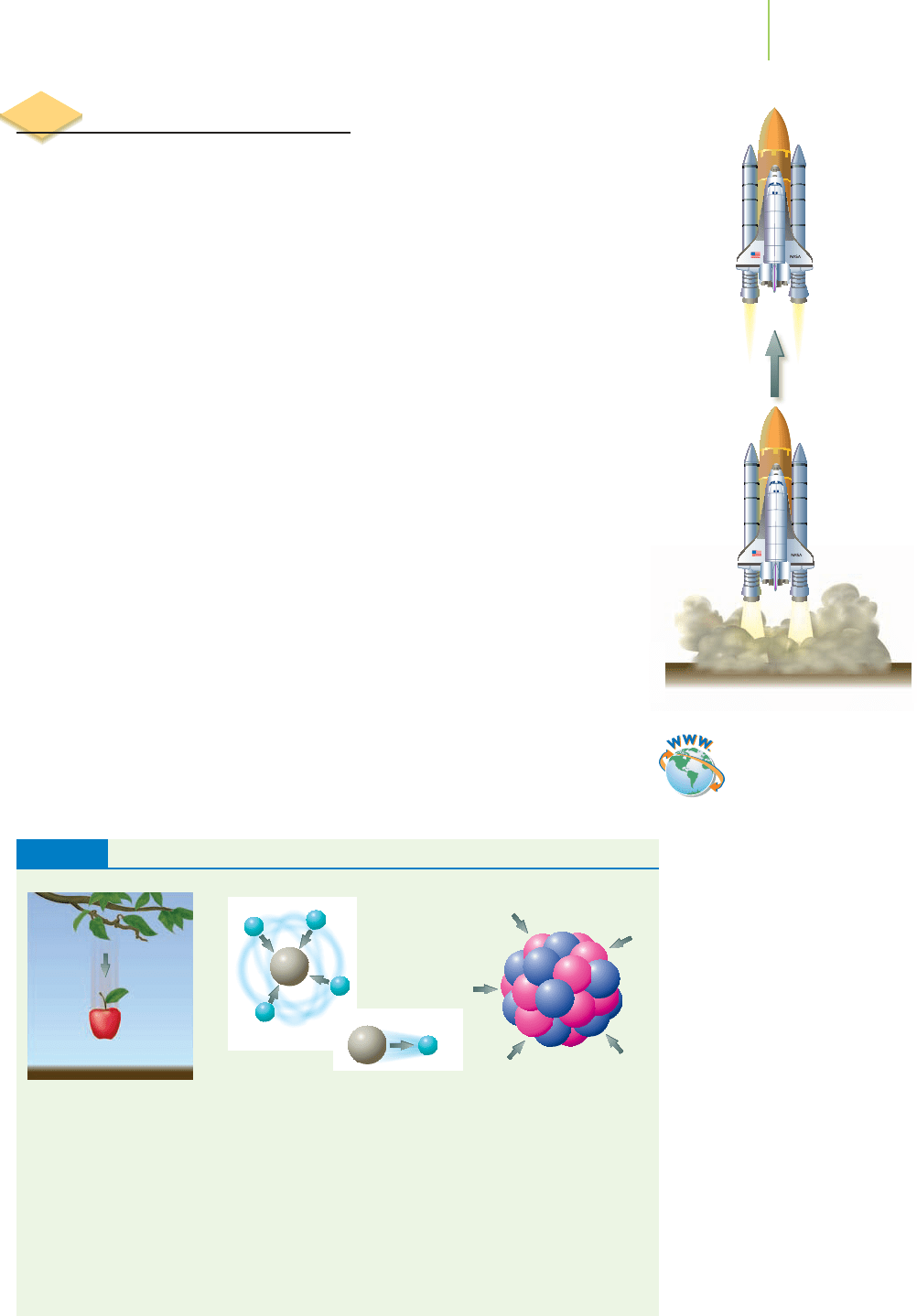
A space shuttle launch is an awe-inspiring

demonstration of the ability of energy to trans-

port humans and material away from Earth’s surface

with an eye toward planetary exploration. The energy to

launch the craft and its crew comes from the explosive vio-

lence of chemical reactions. When these reactions are used in a

carefully controlled way, they can lift the massive shuttle (which

weighs in at a robust 2,000,000 kg), the booster rockets, and the fuel tank

and propel the ship into orbit hundreds of miles above Earth in a very brief

10-minute ride.

Two chemical reactions, indicated in Figure 5.1, power the launch of the space

shuttle. The combustion of hydrogen gas (the combination of hydrogen and oxygen

to form water) takes place in the main engines. At the same time, the solid rocket

boosters attached to the sides of the shuttle release a host of products resulting from

the oxidation of aluminum by ammonium perchlorate, though we show only the

primary equation here.

Main engines: 2H

(g) + O

(g) →2H

O(g)

Boosters: 10Al(s) + 6NH

ClO

(s) → 5Al

(s) + 6HCl(g) + 3N

(g) + 9H

O(g)

As the shuttle sits on the launch pad, it is hard to believe that the en-

ergy that will launch it with such a spectacular display of chemical mus-

cle is quietly present within the main fuel tank and the solid fuel of the

booster rockets. Chemicals can store huge amounts of energy in this

way—and then release it, with very dramatic effects, as soon as a chemi-

cal reaction begins.

These thoughts raise many questions about energy:

What is energy?

The rocket fuels used to lift the space shuttle store energy and release it

during takeoff. How is energy stored within molecules and compounds?

Can we calculate how much energy will be released from a molecule or

compound during a shuttle launch so that enough will be harnessed to

allow the shuttle to climb to exactly the intended orbit? These questions

can be answered by focusing our attention on a branch of science known

thermodynamics. Thermodynamics is concerned with the interconver-

sion of different forms of energy. The speciﬁc area of thermodynamics

most relevant to chemical reactions is known as

thermochemistry, the

study of energy changes and exchanges in chemical processes.

In order to properly describe energy exchanges, we must clearly state

where they occur. We deﬁne the

system as that object

in which we are interested. In our discussion, the

main shuttle craft is the system. Everything else is

deﬁned as the

surroundings. Energy that is lost by the

shuttle’s main engines in our system is gained by

the atmosphere, the surroundings. The system and

the surroundings combine to make up the

universe.

These terms are fundamental to our discussion of

energy in chemistry.

Application

HEMICAL ENCOUNTERS:

Setting the Stage with

the Space Shuttle

(g) + O

(g)

10Al(s) + 6NH

ClO

(s)

5 Al

(s) + 6HCl(g) +

(g) + 9H

O(g)

FIGURE 5.1

The reactions that provide the energy to

lift the space shuttle into orbit.

System

(shuttle,

payload, people)

Surroundings

Universe = System + Surroundings

The system and the

surroundings make up

the universe.

5.1 The Concept of Energy

The simplest commonly used deﬁnition of energy is that it is “the capacity to do

work.”Often it is deﬁned as “the capacity to do work or produce heat.”In order to

fully understand the deﬁnition of energy, we need to deﬁne work.

Work is done whenever any force is used to move an object some distance. For

example, suppose we use a chemical reaction to propel a heavy weight, such as the

space shuttle, upward. We are using the reaction to provide the force that makes

the shuttle move. The chemicals that are combined in the reaction are doing work

on the shuttle, so they are releasing energy. Why does it take so much energy to lift

the shuttle? You might say, “Because the shuttle is very heavy,” but that is only the

beginning of the answer. The shuttle is heavy because of the force of gravitational

attraction between the particles in this system and the rest of planet Earth. To

raise the shuttle, we must make it move against the force of gravity, one of the

three known fundamental forces of nature listed in Table 5.1. Since the force of

gravitational attraction is so large between the shuttle and Earth, we must supply

a lot of energy to raise the shuttle into orbit. The result is that a tremendous

amount of work is done on the shuttle.

We can therefore also describe energy as the capacity to move something

against a fundamental force. This idea can help us develop a good understanding

of what energy is all about. In terms of the system and the surroundings, we can

make the following statement:

Energy is absorbed by the system from the surroundings in order to oppose a

natural attraction.

This means, for example, that energy must be added to two magnets that are stuck

together (a system) in order to pull them apart, because we are opposing their nat-

ural magnetic attraction.Similarly,whenwe pull an electronaway from a nucleus in

an atom (another system),energy is required (must be added to the system) because

opposite charges attract and we are opposing that natural attraction. Figure 5.2

illustrates the energy exchange between the system and surroundings in this case.

5.1 The Concept of Energy 169

Earth

Work moves

the space

shuttle away

from Earth.

The Three Known Fundamental Forces of Nature

TABLE 5.1

–

Gravitational force

causes all objects with

mass to be attracted to

one another.

Electroweak force is responsi-

ble for the attraction between

objects with opposite electric

charges and the repulsion

between objects with the same

electric charge (when it is

known as the electric force), the

phenomena of magnetism and

light, and some transformations

within subatomic particles.

Strong nuclear force

binds protons and

neutrons together

within atomic nuclei.

Tutorial: Work, Heat, and

Energy Flow

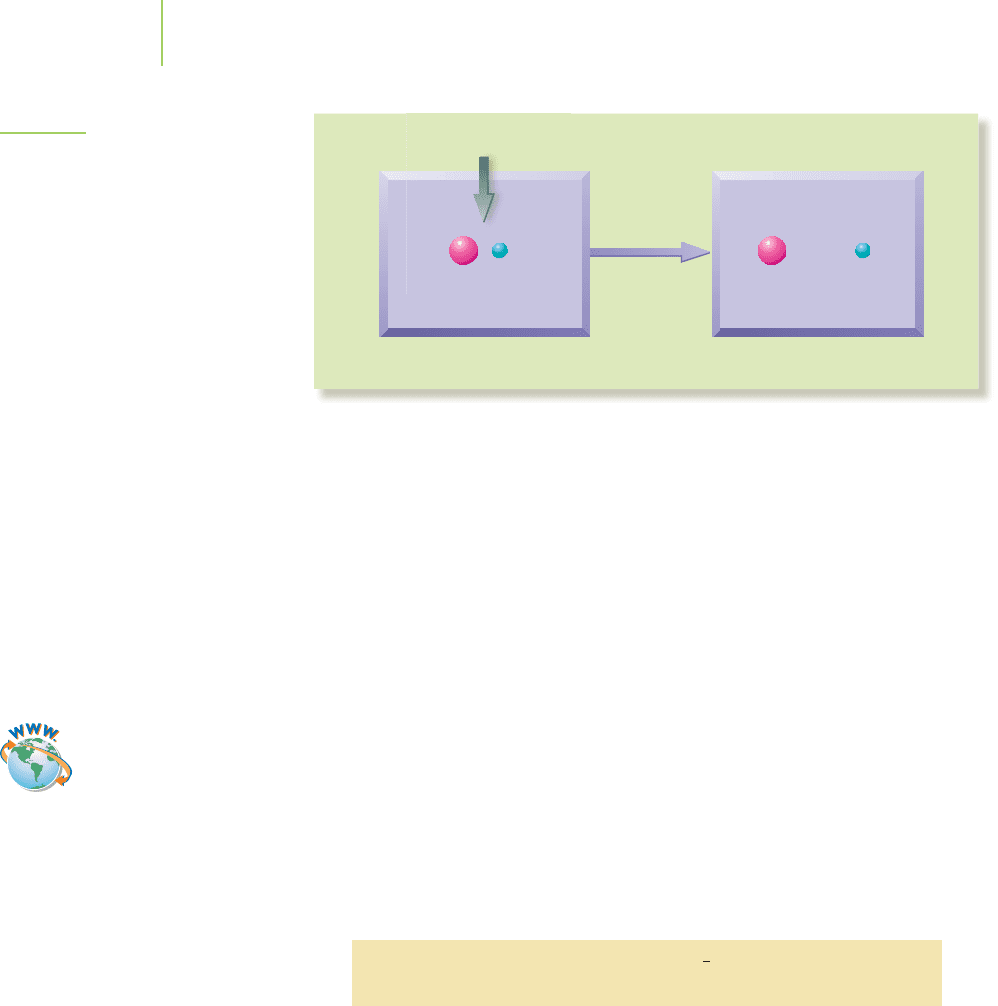
Because energy is needed to oppose a natural attraction, the reverse process allows

us to draw the following opposite, perhaps counterintuitive, conclusion:

Energy is released from the system to the surroundings when a natural attrac-

tion occurs.

This happens when, for example, magnets are made to stick together, an electron

is attracted to an atom, or a ball falls to Earth toward the planet’s center of gravity.

Kinetic Energy Versus Potential Energy

Energy can be relegated to two basic forms: kinetic energy and potential energy.

In addition to these two forms, energy can also be propagated through space in

the form of

electromagnetic radiation, such as light, which we will discuss in detail

in Chapter 6.

Kinetic energy is the energy of movement. Everything that is moving has an

amount of kinetic energy that depends on its mass and velocity, as described by

the equation

Kinetic energy =

where m = mass in kilograms, v = velocity in meters per second.

For example, a 36,000-kg 18-wheeled truck moving at the same speed as an 800-kg

subcompact automobile has more kinetic energy than the car because its mass is

greater.A truck movingfaster thananother,identicaltruck has more kinetic energy

than the slower truck because its velocity is greater. The relationship of kinetic en-

ergy to mass and velocity is true for a car, a truck, a space shuttle—or a molecule.

If movement is associated with energy, then everything that is moving must,

in appropriate circumstances, be able to do work. You can convince yourself of

this by thinking about the steel ball shown in Figure 5.3. If the ball is moving

toward the slope, its energy of movement (kinetic energy) allows it to rise a

certain distance up the slope. The height to which it rises depends on how fast it

was originally moving. Kinetic energy is associated with the work of raising the

ball, and the amount of kinetic energy that the rolling ball possesses will deter-

mine how high it can rise in deﬁance of the gravitational force.

The second fundamental form of energy is

potential energy, which is the en-

ergy that objects possess because of their positions. We often think of potential

energy as stored energy, which, if released, can be transformed into kinetic energy.

For example, any object raised up against the force of gravity gains an amount of

170 Chapter 5 Energy

Energy

Initial state

System:

Surroundings: E

Final state

System:

Surroundings: E

System System

Surroundings Surroundings

FIGURE 5.2

Energy exchange between the system

and the surroundings during the ioniza-

tion of an atom.

Video Lesson: The Nature

of Energy

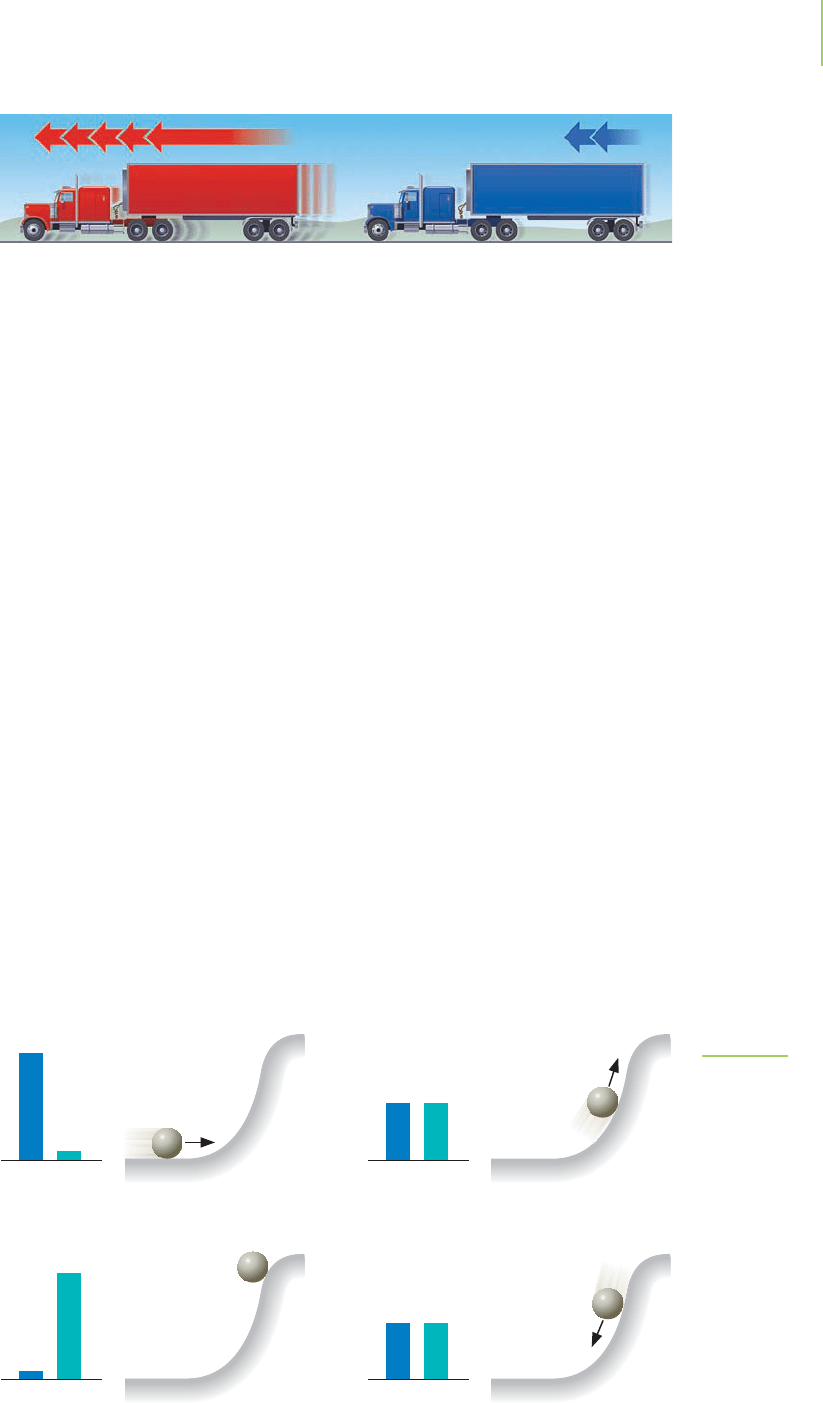
potential energy because of its position relative to the gravitational attraction to

Earth’s center. Recall our key idea that energy is absorbed by the system from the

surroundings in order to oppose a natural attraction. The farther we pull our object

away from Earth’s center of gravity, the more energy is required, and the greater

will be the object’s potential energy.

As our steel ball in Figure 5.3 rises upward, it begins to slow down. In fact, if

we ignore the loss of energy due to friction, the steel ball steadily gains potential

energy in an amount that is equal to the kinetic energy it loses because it is slow-

ing down. By the time the ball becomes stationary at the top of its climb, kinetic

energy due to the rolling of the ball has been converted into potential energy.

What happens next? The potential energy stored in the steel ball due to its rela-

tively high altitude is released as the ball begins to run downhill. The amount of

potential energy is reduced as the kinetic energy, and therefore the velocity of the

ball, increases. At the bottom of the hill, this potential energy has been com-

pletely converted into kinetic energy, and the ball is traveling at its maximum

velocity.

This example of the interconversion between kinetic and potential energy

illustrates one of the most signiﬁcant fundamental laws of nature. It is known as

the

law of conservation of energy:

Energy is neither created nor destroyed. It is only transferred from place to place

and transformed from one form into another.

The energy contained in molecules and compounds, such as those that power

the space shuttle, is a constantly interconverting mixture of kinetic and potential

energy. The particles in the system are moving, bouncing off one another, vibrat-

ing, and rotating as the bonds between atoms stretch in and out, atoms and larger

groups rotate around bonds, and entire molecules cartwheel through space. All

of this motion is associated with a corresponding amount of kinetic energy. The

available potential energy in chemical compounds is stored in the positions and

arrangements of the electrons and nuclei that make up those compounds. For

5.1 The Concept of Energy 171

(a) KE > PE

KE PE

(b) KE = PE

KE PE

(d) KE = PE

KE PE

FIGURE 5.3

A steel ball moving toward a hill demon-

strates that energy can do work and that

kinetic energy and potential energy can

be interconverted. As the ball moves up

the slope, its kinetic energy is converted

into potential energy. When it reaches its

maximum height and begins to fall back,

that potential energy is converted back

into kinetic energy. Work is done when

the mass of the ball rises up the slope.

Assuming they have equal mass, the

faster truck has greater kinetic energy.

instance, as we discussed previously, it takes energy to move an electron away

from an atom’s nucleus, against the pull of the electric force, in just the same way

as it takes energy to lift a weight up from the ground against the pull of the grav-

itational force illustrated in Figure 5.4.

It also requires an inﬂux of energy to a system of atoms in order to force two or

more (like-charged) electrons closer together against the repulsion due to the

electric force, or to force two nuclei together against that force. The electrons and

nuclei of chemicals have potential energy as a consequence of their positions in the

electric force ﬁeld, as shown in Figure 5.5, just as objects we lift and throw around

have potential energy due to their positions in the gravitational force ﬁeld.

Any set of compounds, at a given temperature and pressure, contains chemical

energy stored as a result of the motions and positions of their atomic nuclei

and electrons.

When a chemical reaction occurs in a system, new chemicals are formed with

different internal motions, different electron arrangements, and a different total

energy content. Any excess energy must be released to the surroundings, usually

as heat and possibly as light and/or sound. Any energy acquired by the new chem-

icals must come from the surroundings. For example, when hydrogen and oxygen

react to form water in the main engines of the space shuttle, a tremendous

amount of chemical energy is released. This release of energy occurs because the

structure of water molecules embodies much less energy than that of the oxygen

and hydrogen molecules used to form the water. A small fraction of the released

energy is converted into light and sound. The majority of the released energy dra-

matically increases the speed of motion of the particles involved, causing them to

undergo a massive and explosive expansion as all of the very fast-moving parti-

cles bounce off one another. This chemical cyclone of particles within the ex-

panding gas pounds against the inner upper surface of the shuttle engines and

literally pushes the shuttle upward while water vapor escapes from the opening at

the bottom of the engines, as shown in Figure 5.6.

EXERCISE 5.1 Energy in Various Forms

In our day-to-day chats and political or environmental discussions, we speak of

many different kinds of energy, such as that from wind, waves, or fossil fuels. Can

you explain how these forms of energy (wind, waves, and fossil fuels) are related to

the fundamental forms of energy discussed above?

Solution

Wind energy is the energy associated with the movement of air, so it is a form of

kinetic energy. Similarly, wave energy is the energy associated with the movement of

172 Chapter 5 Energy

Force of expanding gases

Gravity

Net force

FIGURE 5.6

Forces acting on the shuttle’s main

engine.

FIGURE 5.4

The gravitational force. Energy is re-

quired to lift an apple from the ground.

The opposing force is gravity.

FIGURE 5.5

Chemical energy. The positions of the nuclei and electrons, as

well as the motions of the particles, are part of the energy

stored in a molecule.

Application

5.1 The Concept of Energy 173

The trapping of the energy of sunlight by green plants is

one of the most signiﬁcant chemical processes on Earth.

What makes it even more interesting is that the process

is achieved by the smallest chemical change. That tiny

change, powered by the absorption of energy from the

Sun, is the transfer of an electron from one molecule to

another. This change begins the process that provides

energy to the plant and allows it to grow.

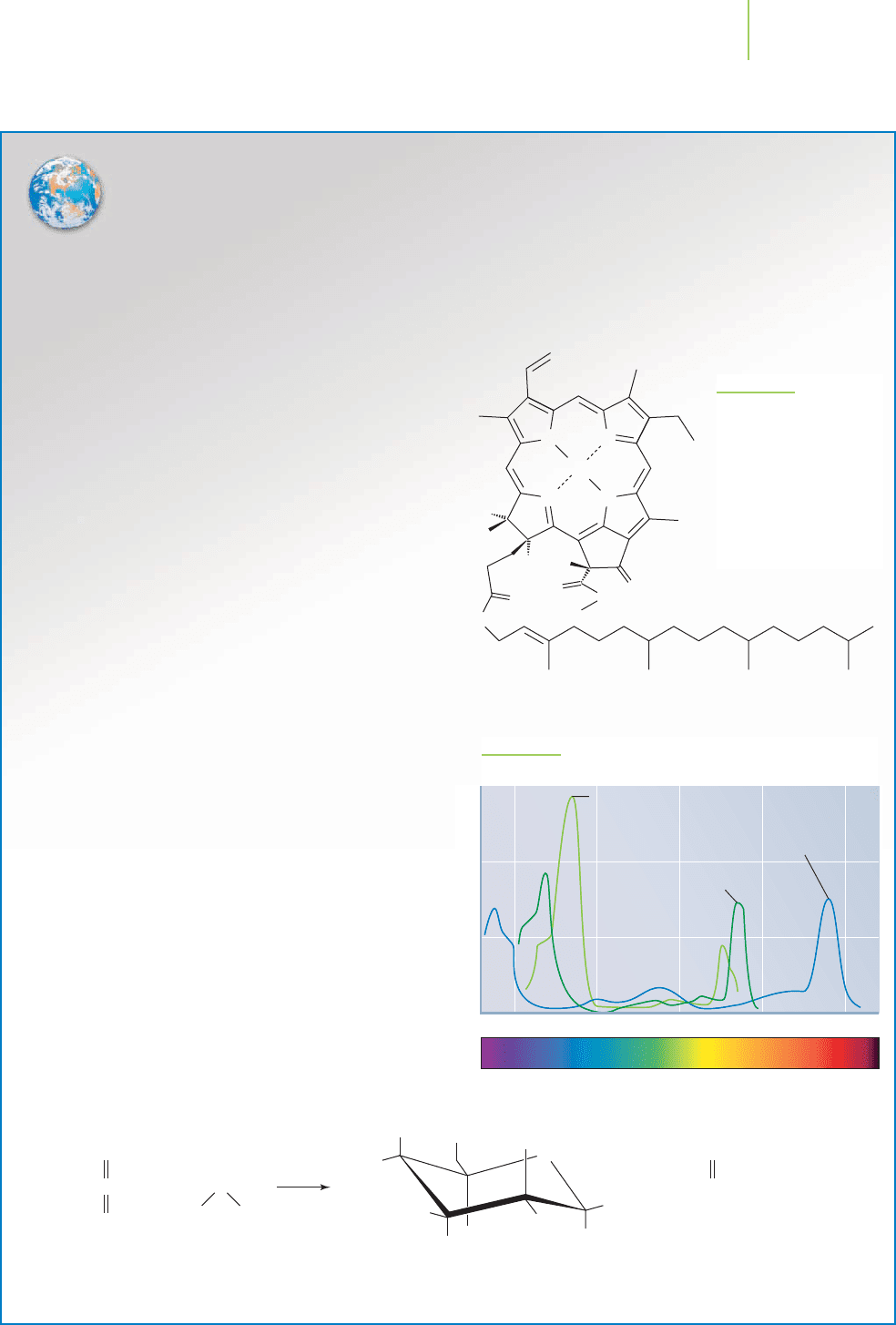
Why are plants green? They contain molecules of

chlorophyll,which absorb light in the red and blue parts

of the visible spectrum (the range of visible colors)

more than in the green parts, leaving the green light to

reach our eyes. There are actually several different types

of molecules known as chlorophyll. Chlorophyll a is

shown in Figure 5.7.

The absorption spectra of some chlorophylls, mean-

ing the extent to which they absorb light of different

wavelengths, is shown in Figure 5.8. Because of differ-

ences in structure, every atom and molecule has its own

absorption ﬁngerprint, which we will discuss more fully

in Chapter 6.

When a molecule absorbs light energy, it usually

raises one or more of the electrons into a higher energy

conﬁguration. When this happens to the chlorophyll in

a plant, an excited higher-energy electron can be trans-

ferred to an adjacent receptor molecule. This electron

transfer requires an input of energy as the negatively

charged electron moves away from a positively charged

atomic nucleus within chlorophyll, against the pull of the

electric force. The transferred electron carries much of

this energy to the receptor molecule.

This is the tiny nanoscale event that powers photo-

synthesis. The transferred electron then moves among a

series of other molecules involved in photosynthesis.

The complex series of steps that each of the molecules

goes through allows some of the energy originally ab-

sorbed from the Sun to be stored within other com-

pounds. Ultimately, the energy from the Sun converts

carbon dioxide and water into carbohydrate and

oxygen—the overall energy-requiring process of

photosynthesis.

The path the energy takes in completing this task is

long. The chemical processes are very complex, and the

involvement of huge numbers of electrons is necessary

to generate signiﬁcant amounts of carbohydrate and

oxygen. But the crucial event begins with a single electron.

NanoWorld / MacroWorld

Big effects of the very small:

Electrons capturing energy in photosynthesis

Chlorophyll a

FIGURE 5.7

Chlorophyll a is a complex

naturally occurring mole-

cule. The transfer of an

electron from chlorophyll,

sunlight, is the key event

of photosynthesis.

FIGURE 5.8

The absorption spectra of a series of chlorophylls.

O+66 +

Carbon dioxide and water combine to make carbohydrates and oxygen.This reaction is driven by the trans-

fer of an electron from chlorophyll.

400 500 600

Wavelength (nm)

Absorption

700 800

Chlorophyll b

Chlorophyll a

Bacteriochlorophyll a

water, so it is a form of kinetic energy. Fossil fuel energy is the energy that we release

from the fossil fuels—coal, oil and natural gas—when we burn them. The energy is

stored within the chemicals involved as a mixture of kinetic and potential energy,

associated with the movement and positions of the particles of the chemicals.

PRACTICE 5.1

Explain how the “activities” of plants are related to the fundamental forms of en-

ergy. Include in your discussion the interaction of plants with the environment and

their ultimate fate as food.

See Problems 1, 2, 5–8, 17, and 18.

Heat and Reaction Proﬁle Diagrams

During a chemical change, energy is exchanged between the system and the sur-

roundings. Much of this energy exchange is as heat.

Heat (q) is the energy that is

exchanged between a system and its surroundings because of a difference in tem-

perature between the two. The temperature of a system is proportional to the

kinetic energy of its particles, and the energy ﬂow as heat between a system and

its surroundings is essentially a transfer of kinetic energy due to the collisions

between particles.

We can portray the change in the internal energy content of chemicals during

a reaction using “reaction proﬁle diagrams” like those shown in Figure 5.9. These

diagrams illustrate the changes in the energy of the components of a reaction as

it progresses. The horizontal axis in the diagram is known as the reaction coordi-

nate, an arbitrary scale that denotes the progress of the reaction from start (left-

hand side) to ﬁnish (right-hand side). The vertical axis represents the relative

energy of the individual components of the system. By comparing the energy of

the starting materials with the products, we can determine the direction of the

ﬂow of energy in the reaction (either from the system to the surroundings or

from the surroundings to the system.)

From the diagram, we note that the curve of the reaction rises to a peak as the

reaction proceeds. This indicates an input of energy needed to drive the reaction

toward products. Virtually all reactions begin with an input of energy, known as

the

activation energy. This energy may be supplied when the overall kinetic

energy of the moving particles is converted into internal potential and kinetic en-

ergy. The chemicals, after colliding, lose energy as they settle into the new chem-

ical arrangement of the products.

A chemical reaction that releases energy as heat to the surroundings, like that

shown in Figure 5.10, is known as an

exothermic reaction. Energy, as heat, ﬂows

out of the system and into the surroundings. A forest ﬁre includes all manner of

174 Chapter 5 Energy

Progress of reaction

Energy

Reactants

Products

Activation

energy: E

Heat evolved

during reaction

Progress of reaction

Energy

Reactants

Products

Activation

energy: E

Heat absorbed

during reaction

FIGURE 5.9

Reaction proﬁle dia-

grams. The exothermic

reaction on the left in-

volves a loss of heat.

The endothermic reac-

tion on the right re-

quires the absorption

of heat.

A forest ﬁre results from many different

exothermic reactions.

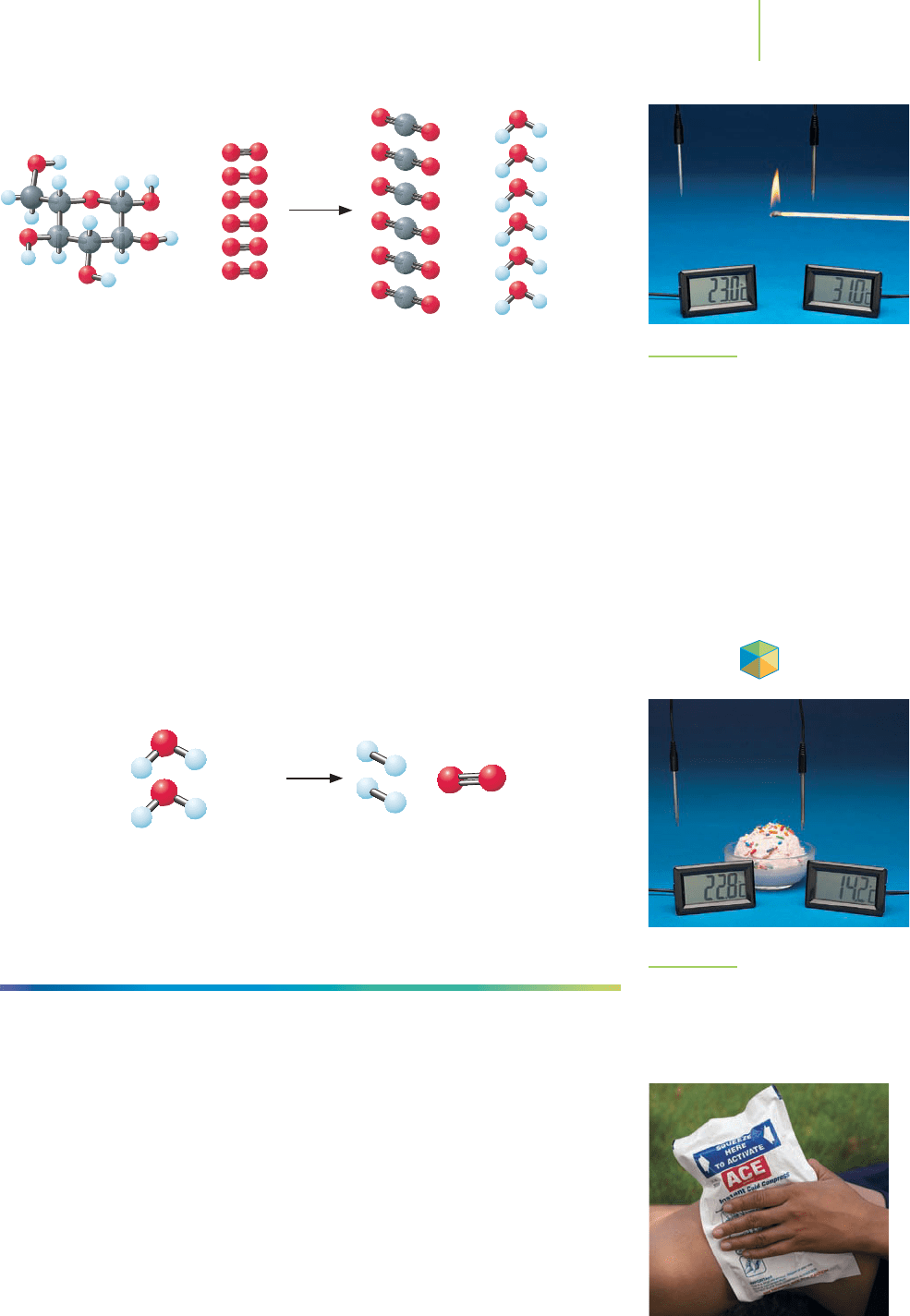
exothermic reactions, releasing torrents of energy as heat to the surroundings.

Cellular respiration, a complex process that we can summarize with the above

equation, is also exothermic. Note that in an exothermic reaction, we can think of

heat as a product of the reaction.

A chemical reaction that absorbs energy as heat is known as an

endothermic

reaction

. In this process, energy as heat ﬂows into the system from the surround-

ings, as illustrated in the melting of ice cream (Figure 5.11). In an endothermic

reaction, such as the formation of oxygen and hydrogen from water, we can think

of heat as a reactant.

Many ammonium salts, such as ammonium nitrate, endothermically dissolve

in water, absorbing energy as heat from the surroundings. Chemical “cold packs”

that are used to cool the injured knee or elbow of an athlete use this concept.

5.1 The Concept of Energy 175

(s) + 6O

(g) 6CO

(g) + 6H

O(l) + heat

Heat

→

The overall equation describing cellular respiration.

FIGURE 5.10

An exothermic process. During chemical

reactions, energy is transferred between

the chemical system and its surround-

ings. Exothermic reactions release energy

from the system into the surroundings.

FIGURE 5.11

An endothermic process. Some chemical

reactions require the transfer of energy

from the surroundings to the system. This

is an endothermic process.

O(l) + heat 2H

(g) + O

(g)

Heat

→

An endothermic reaction requires the addition of heat. In addition to boiling water, the

addition of heat can, under certain conditions, induce a chemical reaction that produces

hydrogen and oxygen.

HERE’S WHAT WE KNOW SO FAR

■

There are three natural forces: the gravitational, electroweak, and strong

nuclear forces.

■

Potential energy is the energy stored within a system.

■

Kinetic energy is the energy associated with motion.

■

The law of conservation of energy states that energy can be neither created nor

destroyed. Instead, it just moves between the system and the surroundings

and can be transformed from one form to another.

■

Work and heat are two ways in which energy can move between the system

and the surroundings.

■

The ﬂow of energy as heat from the system to the surroundings involves an

exothermic process. An endothermic process involves the ﬂow of energy as

heat from the surroundings to the system.

■

Changes in the energy of a reaction can be studied by examining a reaction

proﬁle diagram.

Cold packs use endothermic reactions.

Application

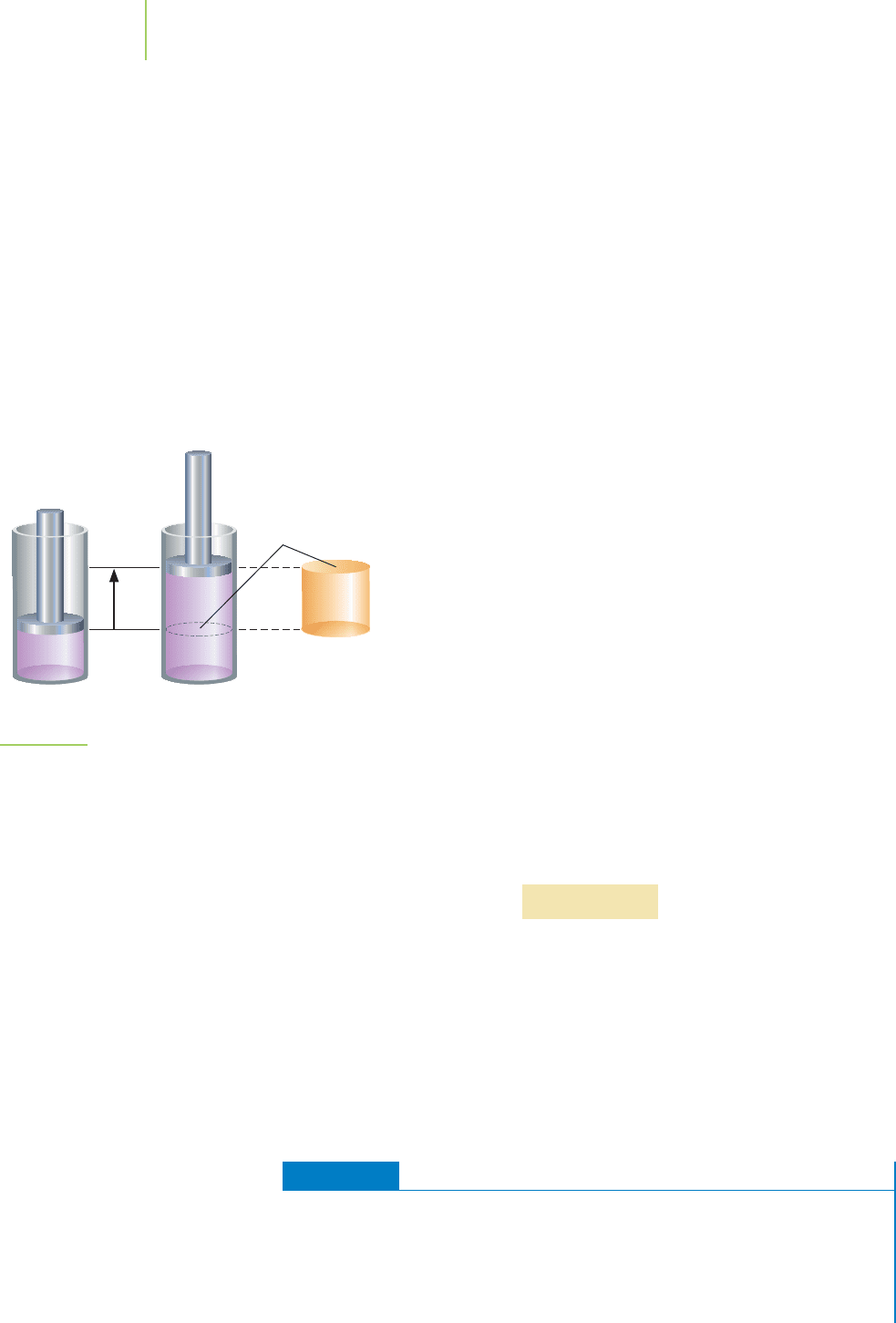
A Closer Look at Work

A system doesn’t contain work. Rather, we can calculate the amount of work that

a system does in moving an object through a distance. Mathematically, we can de-

ﬁne work as the product of the applied force and the distance the object moved.

Work (w) = force (F) × distance (d)

To relate this equation to a chemical system, as is done by the rocket scientist, the

force exerted by an expanding gas is directly related to the product of the pressure

of a system and the area in which it is expanding. Pressure, as we’ll discover in

Chapter 11, is the force exerted by a gas per unit area on the walls of its container.

Force (F) = pressure (P) × area (A)

Substituting this equation into that for the calculation of the amount of work,

we get

Work (w) = P × A × d

This equation can be simpliﬁed by considering the product of

the area (A) multiplied by the height (h), a measure of distance. As

shown in Figure 5.12, the base of the cylinder in the initial ﬁgure

has a known area (A). Moreover, the cylinder has a known height

(h), the distance from the bottom to the top of the cylinder. There-

fore, the gas inside the cylinder has a known volume (V), because

= A × h. In the ﬁnal state in Figure 5.12, the piston has been dis-

placed by a known distance (h). We use the Greek letter  (delta)

to represent the change in some quantity. Therefore, h means “the

change in height.” The resulting three-dimensional measurement

is the change in the volume of the system (V). Speciﬁcally,for this

case, V is the ﬁnal volume of the system minus the initial volume

of the system: V = V

ﬁnal

− V

initial

. In other words, A × hfora

reaction is best represented by V.

Work (w) = pressure (P) × change in volume (V)

Our ﬁnal modiﬁcation to the equation that deﬁnes work is an

adjustment to account for the loss of energy when a system does

work and the gain of energy when a system has work done on it.

We add a negative sign to the equation to illustrate this fact:

w =−PV

This equation indicates that when the volume of a system expands (i.e., V is pos-

itive), work is done by the system, and, as a result, energy is lost from the system

system

= “−”). Conversely, when the volume of a system contracts (i.e., V is

negative), the system gains energy, and work is done on the system (w

system

= “+”).

Because pressure is recorded in atmospheres and volume in liters, the units for

work (energy) are in L·atm. This is mathematically related to the SI unit of energy

known as the joule (J), in honor of the English physicist James Prescott Joule

(1818–1889). We will derive this relationship later, but for now we can assume

that 1 L·atm = 101.3 J.

EXERCISE 5.2 Work, Work, and More Work

Calculate, in L·atm and joules, the work associated with the contraction of a gas

from 75.0 L to 30.0 L at a constant external pressure of 6.20 atm. (1 L·atm = 101.3 J)

First Thoughts

The road signs concerning work can be confusing. When a system expands, work

is done by the system (w

system

= “−”) on the surroundings (w

surroundings

= “+”).

176 Chapter 5 Energy

∆h

(a) Initial state (b) Final state

Area = A

∆V

FIGURE 5.12

Gas expansion does work. The initial volume of the gas in-

creases by an amount ∆V. When the pressure remains

constant, this becomes P∆V, or work.

Conversely, when the system contracts, the surroundings do work on the system

system

= “+”). In this case, the work (from the standpoint of the system) is posi-

tive because the gas is being compressed. In other words, work is being done on the

system.

Solution

V = change in volume = V

ﬁnal

−V

initial

= 30.0 L − 75.0 L =−45.0 L

w =−PV =−6.20 atm × (−45.0 L) =+279 L·atm

converting this to joules, we get

w =+279 L·atm ×

101.3J

L ·atm

=+2.83 × 10

J = 28.3 kJ

Further Insights

The sign on the value of the work term is important to us. Not only does it reﬂect

how much the internal energy of the system changes, but it also indicates the direc-

tion in which it changes. Mathematically, the sign was determined by the direction

of the change in the volume. In our example, the volume of the system is reduced,

so the work done on the system is positive.

PRACTICE 5.2

Calculate, in L·atm and joules, the work associated with the expansion of a gas from

30 L to 300 L at a constant external pressure of 1.0 atm.

See Problems 9, 13d, and 14d.

Internal Energy

The reaction of hydrogen and oxygen in the shuttle’s main engines causes energy

transfer as heat and as work. The clearest result of the work done by this system

is that the shuttle rises upward through Earth’s atmosphere. The reaction also re-

leases energy that heats the internal parts of the craft, along with many molecules

in the atmosphere that come into contact with the hot exhaust vapors from the

reaction.

The total energy of the space shuttle, just as in any other system, is known as

the

internal energy (U) of the system. The internal energy is made up of the sum of

the system’s kinetic and potential energies. Unfortunately, we cannot calculate the

absolute value for the internal energy of a system, because it is extremely difﬁcult

to account for all the individual energies that give rise to the kinetic and potential

energies. However, because the change in the internal energy (U) in a chemical

process is measurable—if we can calculate the exchange of energy as heat (q)

within, and the work done (w) by the system—we can determine the energy

change within the system. This is the

ﬁrst law of thermodynamics:



U = q + w

A word of caution: We must take care with the way in which we attribute positive

or negative values to q and w. If we are looking at things from the point of view of

the system, the loss of heat from the system to the surroundings will carry a nega-

tive sign (q

system

= “−”). Similarly, if the system does work on the surroundings,

system

will have a negative sign (w

system

= “−”). Conversely, the ﬂow of energy as

heat (q) into the system will be a positive value (q = “+”), and if work (w)isdone

on the system by the surroundings, w

system

will be positive (w

system

= “+”).

Because energy can be neither created nor destroyed in a process, the total

amount of energy transferred as heat and work to or from the system is exactly

equal and opposite to that transferred from or to the surroundings.

U

system

=−U

surroundings

5.1 The Concept of Energy 177

The reaction of hydrogen and oxygen in

the main shuttle engine produces heat

and does work on the surroundings.

Video Lesson: The First Law

of Thermodynamics

Video Lesson: Work

Video Lesson: Heat

Visualization: Work vs. Energy

Flow