Kelter P., Mosher M., Scott A. Chemistry. The Practical Science

Подождите немного. Документ загружается.

For NH

2 mol N

14.01 g N

1 mol N

28.02 g N

4 mol H

1.008 g H

1 mol H

4.032 g H

3 mol O

16.00 g O

1 mol O

48.00 g O

Molar mass

= 80.05 g

Mass percent nitrogen =

mass total N

mass total compound

× 100%

28.02

80.05

× 100% = 35.00%

For (NH

)

2 mol N

14.01 g N

1 mol N

28.02 g N

8 mol H

1.008 g H

1 mol H

8.064 g H

1 mol S

32.07 g S

1 mol S

32.07 g S

4 mole O

16.00 g O

1 mol O

64.00 g O

Molar mass

= 132.15 g

Mass percent nitrogen =

mass total N

mass total compound

× 100%

28.02

132.15

100% = 21.20%

The results indicate that any chosen mass of NH

contains a signiﬁcantly

greater percentage of nitrogen (35.00%) than does the same mass of (NH

)

(21.20%).

EXERCISE 3.7 Calculating Mass Percent

Phosphorus is another element that is vital for plant growth. Many fertilizers

therefore also contain phosphorus and are sold on the basis of the percentage of

phosphorus in the fertilizer. One example is calcium dihydrogen phosphate,

Ca(H

)

. The fertilizer, commonly known in the agriculture industry as “triple

superphosphate,” is a granular substance that is made from phosphoric acid and

phosphate rock and is used in fertilizing grain ﬁelds and sugar cane. What is the

mass percent of phosphorus in triple superphosphate?

Solution

The compound’s molar mass is 234.05 g/mol. The 2 phosphorus atoms contribute

30.97

2 = 61.94 g per formula unit. The mass percent of phosphorus is

Mass percent

61.94 g P

234.05 g compound

× 100% = 26.46% P

98 Chapter 3 Introducing Quantitative Chemistry

Application

HEMICAL

ENCOUNTERS:

A Focus on

Chocolate

PRACTICE 3.7

Some mineral supplement tablets contain potassium in the form of potassium chlo-

ride (KCl). What is the mass percent of potassium in this compound?

See Problems 37–48.

HERE’S WHAT WE KNOW SO FAR

■

Formula masses are calculated by adding the average atomic masses of the

individual atoms in a formula.

■

Chemists count molecules in a sample by measuring its mass.

■

Masses can be converted into moles by using the molar mass of a compound.

■

One mole of any substance is 6.022

entities.

■

The mass percent of a component in a substance is the total mass of the

component divided by the total mass of the substance, and then multiplied

by 100%.

3.5 Finding the Formula

For many people, chocolate is close to being essential for life! Per-person con-

sumption in 2000 was 22.4 lb in Switzerland and 11.6 lb in the United States.

Chocolate is big business. For instance, in 2002, U.S. manufacturers shipped over

1.5 billion kg (3.3 billion lb) of chocolate, worth $8.5 billion. This includes not

only candy bars but also powdered chocolate for drinks and baking. How is

chocolate made? It is harvested from cacao beans from a tree aptly named Theo-

broma cacao. Theobroma means “food of the gods” (Figure 3.9).

A multitude of compounds make up the ﬂavor of chocolate. One of these is

named 2,5-dimethylpyrazine. To work with this compound in chemistry, it

is necessary to have its empirical and molecular formulas. These are found by

experimentally determining the mass percent of the elements present in a sample

of the compound. 2,5-Dimethylpyrazine, for example, contains, by mass,

66.62% carbon, 7.47% hydrogen, and 25.91% nitrogen. How can we use these re-

sults to calculate the molecular formula of 2,5-dimethylpyrazine? We can begin

3.5 Finding the Formula 99

FIGURE 3.9

Theobroma cacao and the food of the gods.

Video Lesson: Finding Empirical

and Molecular Formulas

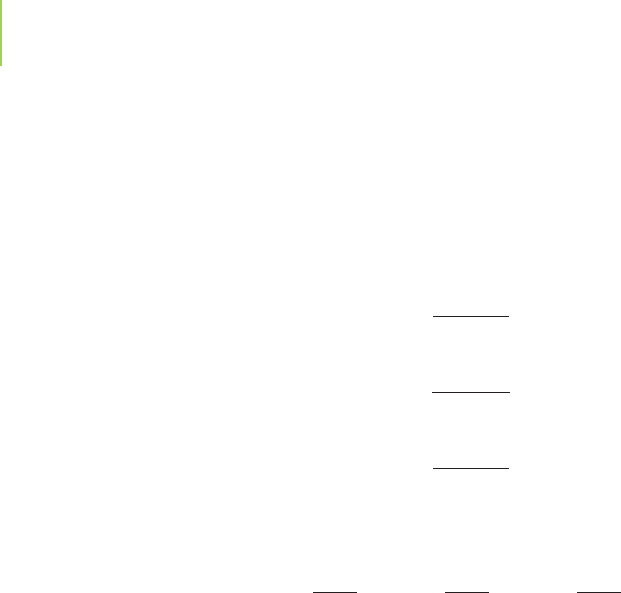
by calculating the ratio in which the atoms of the elements are present in the

compound. To do this, we convert the mass ratio obtained from the analysis

experiment into a mole ratio. The process is made simpler because the mass

percent data tell us how many grams of each element are present in 100 g of

the compound. That is, 66.62% carbon means that in every 100 g of

2,5-dimethylpyrazine, 66.62 g are carbon. This is our starting point for the

conversion into moles.

66.62 g C

1 mol C

12.01 g C

5.547 mol C

7.47 g H

1 mol H

1.008 g H

7.41 mol H

25.91 g N

1 mol N

14.01 g N

1.849 mol N

If we divide all these mole values by the smallest mole value (1.849), we will ob-

tain the simplest whole-number ratio of the atoms that make up the substance.

5.547

1.849

= 3

7.41

1.849

= 4

1.849

= 1

In this case, the division step yields the simplest whole-number ratio immedi-

ately. We know that it is the simplest whole-number ratio because the ratio 3:4:1

cannot be reduced further. We can now write the empirical formula for the com-

pound as

The numbers will not always work out as neatly as that, sometimes because of

experimental errors and sometimes because the formula is a little more complex.

For example, if for a different compound we experimentally obtained the results

1.506 mol C 3.007 mol H 1.008 mol O

they could reasonably be simpliﬁed to this ratio:

1.5 mol C 3 mol H 1 mol O

This ratio is not the simplest whole-number ratio that we need in order to write

an empirical formula. However, it can be converted into the simplest whole-

number ratio by multiplying all the numbers by 2. When we do this, we get

3 mol C, 6 mol H, and 2 mol O, which gives the empirical formula C

. This

illustrates that when we’re trying to ﬁnd the simplest whole-number ratio, we can

multiply or divide the set of values by any number we choose, because the ratio

will remain the same provided that we perform the same multiplication or divi-

sion on each value. However, we always choose the number that provides the sim-

plest whole-number ratio of atoms in the formula.

The empirical formula of 2,5-dimethylpyrazine, the chocolate ﬂavoring mol-

ecule, is C

N. This formula tells us only the ratio in which the elements are

present. It does not tell us the molecular formula, which is the actual number of

each type of atom in a molecule of the compound. To determine the molecular

formula, we would need to know the average molecular mass of the compound,

which can be determined experimentally via the technique of mass spectrometry,

introduced in Section 2.5. This would reveal that the average mass of one mole-

cule of the compound is 108.1 amu, corresponding to a molar mass of 108.1 g.

What is the average molecular mass of the empirical formula?

If we add together the masses of the atoms in the empirical formula, we get a

total of 54.07 amu (or g/mol).

100 Chapter 3 Introducing Quantitative Chemistry

3 mol C

12.01 g

1 mol C

= 36.03 g

4 mol H

1.008 g H

1 mol H

= 4.032 g

1 mol N

14.01 g N

1 mol N

= 14.01 g

= 54.07 g C

N per mole

The average molecular mass is greater than this value, so we have to work out how

many times that value must be multiplied to obtain the average molecular mass.

Because 2 × 54.07 = 108.1, the molecular formula for 2,5-dimethylpyrazine

must be C

, derived from (C

N) × 2. There are two empirical formula

units per molecule of 2,5-dimethylpyrazine.

EXERCISE 3.8 Alkynes Rule the World: Empirical and Molecular Formulas

An alkyne is a special class of molecules that have a particular arrangement of atoms

that make them useful in the manufacture of pharmaceuticals and polymers. One

alkyne with a molar mass of 54.09 g was determined to have 11.18% hydrogen and

88.82% carbon. What is the empirical formula? What is the molecular formula?

Solution

We ﬁrst assume that we have 100 g of the alkyne. Then

11.18 g H ×

1 mol H

1.008 g

= 11.09 mol H 88.82 g C ×

1 mol C

12.01 g

= 7.396 mol C

We next determine the simplest whole-number ratio between these two values.

11.09 mol H

7.396 mol C

= 1.499 H

7.396 mol C

= 1.000 C

Multiplying these by 2, we get the empirical formula for the alkyne:

The molar mass of this empirical formula is 27.04 g. Given that we need 54.09 g to

obtain the molecular formula, we can reason that the correct molecular formula

must be C

PRACTICE 3.8

What are the empirical formula and the molecular formula of a compound that

contains 92.26% carbon and 7.74% hydrogen, if the molar mass of the substance is

78.11 g/mol?

See Problems 49–52.

EXERCISE 3.9 Determining the Formula of Heme

Oxygen is carried around your body bound to iron ions that are part of a “heme”

chemical group, which is part of the protein we call hemoglobin. The heme portion

of hemoglobin has a molar mass of 616.5 g. The percent composition of heme,

rounded to three signiﬁcant ﬁgures, is

66.4% C 5.24% H 9.09% Fe 9.09% N 10.4% O

From these data, calculate the empirical and molecular formulas for this key bio-

chemical molecule.

3.5 Finding the Formula 101

Empirical formula

Molecular formula

341

682

2,5-Dimethylpyrazine

But

Hemoglobin

102 Chapter 3 Introducing Quantitative Chemistry

Solution

We ﬁrst convert the percentages listed into grams by assuming that we have a 100.0-g

sample of heme and then convert the grams into moles by dividing each quantity by

the molar mass of the appropriate element. We are retaining an extra (insigniﬁcant)

ﬁgure throughout the intermediate calculations. We drop all insigniﬁcant ﬁgures at

the end.

66.4 g C ×

1 mol C

12.01 g C

= 5.529 mol C

5.24 g H ×

1 mol H

1.008 g H

= 5.198 mol H

9.09 g Fe ×

1 mol Fe

55.85 g Fe

= 0.1628 mol Fe

9.09 g N ×

1 mol N

14.01 g N

= 0.6488 mol N

10.4 g O ×

1 mol O

16.00 g O

= 0.6500 mol O

Divide each number by the smallest to determine the simplest whole-number ratio:

5.529 mol C

0.1628

33.96 mol C

5.198 mol H

0.1628

= 31.93 mol H

0.1628 mol Fe

0.1628

1.000 mol Fe

0.6488 mol N

0.1628

3.985 mol N

0.6500 mol O

0.1628

= 3.993 mol O

These numbers round off to this empirical formula:

FeN

The molecular formula for heme either will be the same as the empirical formula or

will correspond to the empirical formula multiplied by some whole number. If we

calculate the molar mass corresponding to the empirical formula, we get

(12.01×34) + (1.008 ×32) + (55.85 ×1) + (14.01 ×4) + (16.00 ×4)

= 616.5 grams per mole.

Because we were told that the molar mass of heme is 616.5, we can say that the mol-

ecular formula for heme is also C

FeN

PRACTICE 3.9

Acommoncomponent of several wines thathavegonebad—they tastelikevinegar—

is a compound with an average molecular mass of 60.06 amu and the composition

40.0% C, 6.70% H, 53.3% O. Calculate the molecular formula of this compound,

which is called ethanoic acid (or, commonly, acetic acid).

See Problems 53–58 and 96.

102 Chapter 3 Introducing Quantitative Chemistry

HC OH

Salicylic acid Ethanoic anhydride

Reactants Products

Acetylsalicylic acid Ethanoic acid

(acetic acid)

O O

HC OH

3.6 Chemical Equations

We now have sufﬁcient background to explore how the techniques introduced up

to this point in the chapter are put to use in the study of chemical change. The

fundamental process of change in chemistry is the chemical reaction. For example,

the ﬁnal step in the manufacture of aspirin is the reaction shown below.

3.6 Chemical Equations 103

Application

HEMICAL ENCOUNTERS:

Preparation of Aspirin

Salicylic acid and ethanoic anhydride (acetic anhydride) are the reactants of

this reaction, which means they are the chemicals present at the start of the reac-

tion. Aspirin and ethanoic acid (acetic acid) are the

products, the chemicals pro-

duced as a result of the reaction.

How do we know how much of our reactants we

must combine to get the quantity of aspirin we want to produce?

For this or any

other chemical reaction, the key is to understand the proportions in which the re-

actants react and in which the products are formed. That information, and all the

other key aspects of a reaction, can be summarized in a

chemical equation,

another example of the “chemist’s shorthand.”

A chemical equation uses chemical formulas to indicate the reactants and

products of the reaction. The equation also indicates the proportions in which the

chemicals involved react together and are formed. The ﬁrst step in writing a

chemical equation is to write the formulas or structures of all the reactants and

products, with an arrow between them indicating the course of the reaction. For

the synthesis of aspirin, this beginning is

+ C

→ C

+ C

We know that during a reaction, atoms cannot be created or destroyed but are

simply rearranged. We describe this by saying that equations must be

balanced to

be accurate descriptions of a chemical change. This means that all of the atoms

that appear on the left-hand side of the equation, within the reactants, must

also appear on the right-hand side, within the products. We can check whether

an equation is balanced by counting the atoms on each side of the equation

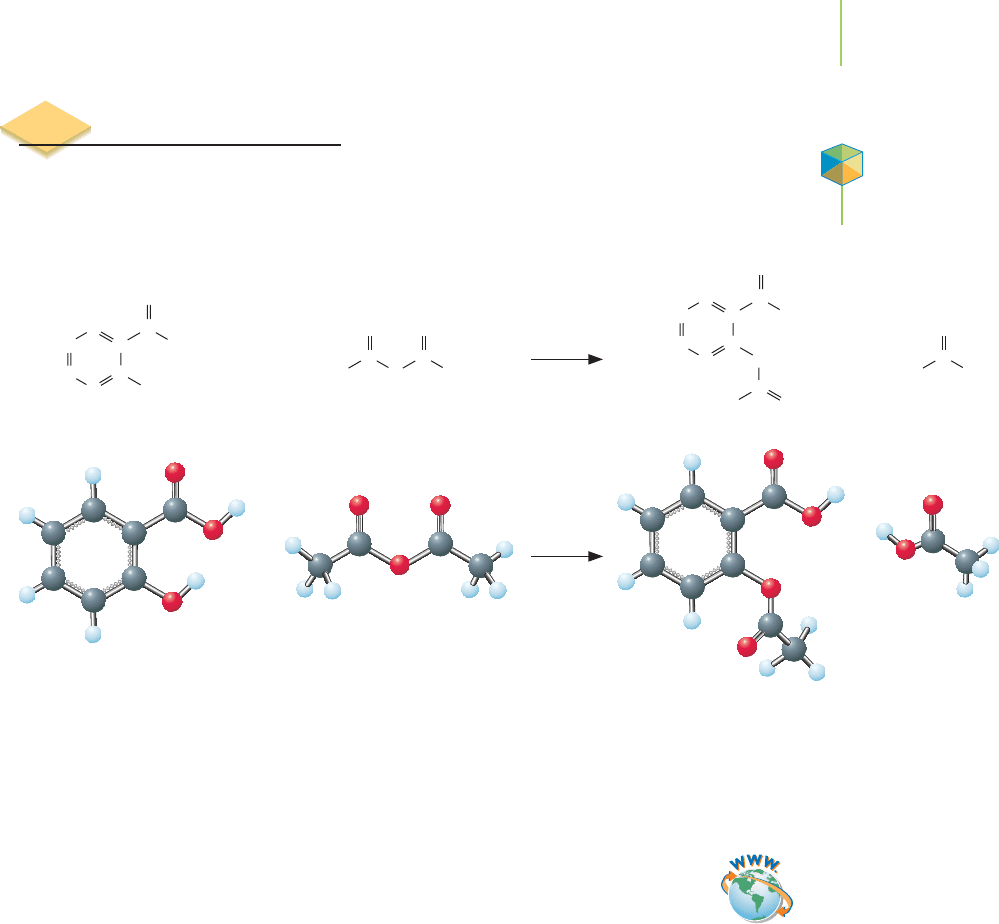
(Figure 3.10).

Therefore in this case, the equation we found in our beginning step is bal-

anced, because the number of each type of atom in the reactants is equal to the

number of that type of atom in the products. The equation represents a re-

arrangement of the atoms, but no atom is created or destroyed; matter in the

Video Lesson: Balancing

Chemical Equations

Video Lesson: An Introduction

to Chemical Reactions and

Equations

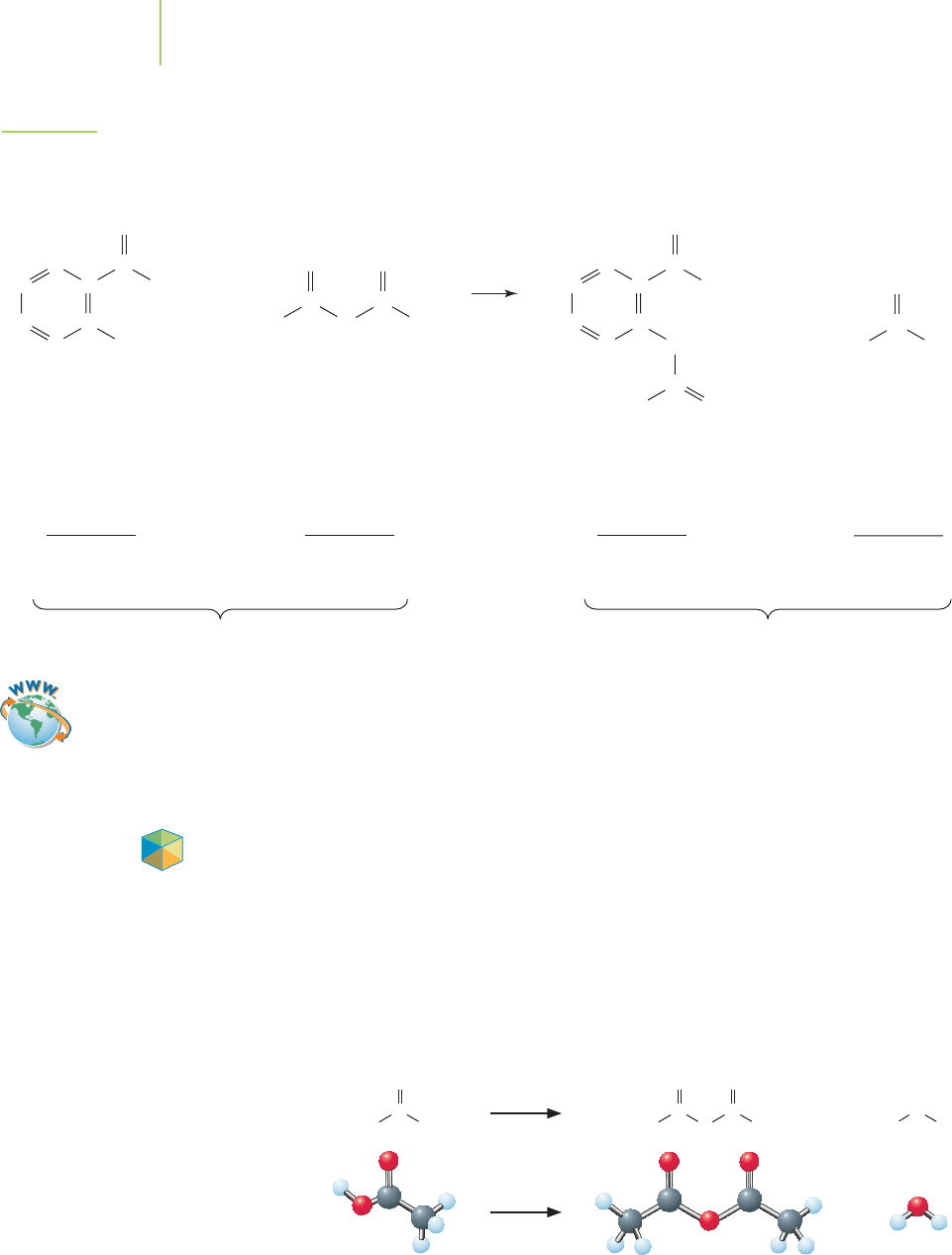
104 Chapter 3 Introducing Quantitative Chemistry

Salicylic acid Ethanoic anhydride Aspirin Ethanoic acid

7 carbons

6 hydrogens

3 oxygens

138 amu

scales to

1 mol  138 g

240 g total 240 g total

4 carbons

6 hydrogens

3 oxygens

102 amu

scales to

1 mol  102 g

9 carbons

8 hydrogens

4 oxygens

180 amu

scales to

1 mol  180 g

2 carbons

4 hydrogens

2 oxygens

60 amu

scales to

1 mol  60 g

CHC

FIGURE 3.10

A chemical equation has the same number and type of each atom on each side of the arrow. Note

that the mass of the products equals the mass of the reactants. Ethanoic anhydride and ethanoic

acid are commonly known as acetic anhydride and acetic acid, respectively.

equation is conserved. Many equations, however, are not balanced when we sim-

ply write down the formulas for the reactants and products. In order to ﬁx this

problem and balance these reactions, we have to use some reasoning to discover

the true proportions in which the chemicals react and are formed.

Balancing Equations

The ethanoic anhydride used in the synthesis of aspirin is a very versatile com-

pound that is used in many other chemical-manufacturing processes, such as the

production of ﬁbers, plastic materials, and pharmaceuticals. One way to make

ethanoic anhydride on an industrial scale is by heating ethanoic acid in the pres-

ence of quartz or porcelain chips.

This causes a “dehydration” reaction, in which water is removed from the reac-

tants and becomes an additional product. To analyze the quantitative relationships

among the chemicals involved in the manufacture of ethanoic anhydride, we

need to write the balanced chemical equation for the process. The structures of

the reactants and products are shown below.

Application

O O

Ethanoic anhydrideEthanoic acid

(acetic acid)

Water

The ﬁrst step in balancing the equation is to write down the formulas of the

reactants and products, as follows:

→ C

+ H

But this equation is not balanced (Figure 3.11).

Visualization: Conservation of

Mass and Balancing Equations

Tutorial: Balancing Chemical

Equations

Ethanoic acid Ethanoic anhydride

120 g total 120 g total

2 carbons

4 hydrogens

2 oxygens

60 amu each

scales to

2 mol  120 g

4 carbons

6 hydrogens

3 oxygens

102 amu

scales to

1 mol  102 g

2 hydrogens

1 oxygen

18 amu

scales to

1 mol  18 g

冢冣

FIGURE 3.12

The equation is now balanced.

To make this equation mathematically valid, we must balance it. We’ll do this

by adjusting the numbers of the compounds until the numbers of atoms of each

type are the same on both sides of the equation. We cannot simply change any

of the formulas we have written; doing so would change the substances in the reac-

tion! The only thing we can do to balance an equation is to use multiples of the

correct formulas in order to ﬁnd the proportions that would produce a balanced

equation. We indicate the desired multiples by placing numbers in front of the

formulas. We call these numbers the

coefﬁcients in an equation. For example, we

could change the equation for the formation of ethanoic anhydride to read

→ C

+ H

We chose to add the coefﬁcient 2 because we noticed that there were 4 carbons on

the right-hand side and only 2 on the left-hand side of the unbalanced equation.

Placing the coefﬁcient 2 before the formula for ethanoic acid changes the mean-

ing of the equation. In this case, it indicates that 2 molecules of ethanoic acid

react to produce 1 molecule of ethanoic anhydride and 1 molecule of water.

Alternatively, we can say 2 mol of ethanoic acid react to produce 1 mol of

ethanoic anhydride and 1 mol of water. Check that you agree that the equation is

now balanced, as shown in Figure 3.12. You should ﬁnd that each side of the

equation now contains 4 carbon atoms, 8 hydrogen atoms, and 4 oxygen atoms.

We have determined the proportions in which these reactants and products can

be combined into a feasible chemical reaction.

3.6 Chemical Equations 105

Ethanoic acid Ethanoic anhydride

60 g total 120 g total

2 carbons

4 hydrogens

2 oxygens

60 amu

scales to

1 mol  60 g

4 carbons

6 hydrogens

3 oxygens

102 amu

scales to

1 mol  102 g

2 hydrogens

1 oxygen

18 amu

scales to

1 mol  18 g

FIGURE 3.11

This equation is not balanced.

106 Chapter 3 Introducing Quantitative Chemistry

EXERCISE 3.10 Balancing Equations

1. Consider the production of hydrogen via the reaction of ethane (C

) with

steam. This process is completed in industry to make a mixture of carbon

monoxide (CO) and hydrogen gas (H

) known as “synthesis gas.” The

hydrogen can be separated from the other gases by passing it through a ﬁlter

that selectively adsorbs the CO. This process is known as pressure swing

adsorption. What is the balanced equation for the reaction of ethane with

steam?

2. Butane (C

) is a fuel that reacts with oxygen in the air to produce carbon

dioxide and water. What is the balanced equation describing the reaction of

butane and oxygen?

Solution

1. The chemical reaction is

+ H

O → CO + H

In this reaction, all of the hydrogen appears in two reactants, and all other

elements are in just one compound on each side. Therefore, we avoid

hydrogen and balance elements that appear only once. Let’s begin with carbon.

❚ Balancing carbon: There are 2 C’s on the left and one on the right, so we

multiply the CO by 2.

+ H

O → 2CO + H

❚ Balancing oxygen: There is 1 O on the left and 2 O’s on the right, so we

must multiply H

O by 2.

+ 2H

O → 2CO + H

❚ Balancing hydrogen: There are now 10 H’s on the left (6 +2 × 2) and 2 on

the right, so we must multiply H

by 5 (5 × 2 =10) to get 10 H’s on the right.

+ 2H

O → 2CO + 5H

❚ Checking our work: We have 2 C’s, 10 H’s, and 2 O’s on the left. We have

2 C’s, 10 H’s, and 2 O’s on the right. The reaction is, in fact, now an equation

as written. Note that throughout this process, we multiplied only entire

compounds. We did not change their structure or add compounds that were

not already part of the reaction.

+ 2H

O → 2CO + 5H

2. The reaction described is

+ O

→ CO

+ H

Following the same procedure, we note that oxygen appears in two

compounds of the products, so we avoid oxygen and balance the other

elements ﬁrst.

❚ Balancing carbon: There are 4 C’s on the left side and 1 C on the right. We

multiply CO

by 4 to balance carbon.

+ O

→ 4CO

+ H

❚ Balancing hydrogen: There are 10 H’s on the left and 2 on the right, so we

must multiply H

O by 5.

+ O

→ 4CO

+ 5H

❚ Balancing oxygen: There are now 2 O’s on the left and 13 (2 × 4 + 5) on the

right, so we must multiply O

(

× 2 = 13) to get 13 O’s on the left.

→ 4CO

+ 5H

Although the equation is now mathematically balanced (and perfectly

acceptable), it is common practice to clear the fraction. In this case, we

multiply all quantities by 2, giving the ﬁnal equation:

+ 13O

→ 8CO

+ 10H

After balancing, we have 8 C’s, 20 H’s, and 26 O’s on the left, and we have

8 C’s, 20 H’s, and 26 O’s on the right. All is well.

PRACTICE 3.10

Balance this equation for the reaction that produces phosphoric acid (H

which can be used as a fertilizer, and calcium sulfate, forming gypsum used in hous-

ing wallboard.

(PO

)

+ H

→ CaSO

+ H

See Problems 59–64.

More Information from the Equation

As you will learn as you continue your chemistry studies, the chemical equation

contains a great wealth of information about a reaction. The chemical equation

can also provide information about the states, or phases, of reactants and prod-

ucts. In Chapter 1, we discussed the states of matter.

Phase is another term for the

state of matter, a part of matter that is chemically and physically homogeneous.

This is often indicated by using italic letters in parentheses after each formula in

the equation.

(s)

= the solid phase

(l)

= the liquid phase

(g)

= the gaseous phase

(aq)

= aqueous phase solutions (solutions in water)

For example, the equation we balanced in Exercise 3.10, butane gas reacting with

oxygen gas to produce carbon dioxide gas and liquid water, could be written to

include this information. This equation speciﬁcally says that 13 mol of oxygen

gas reacts with 2 mol of butane gas to produce 8 mol of carbon dioxide gas and

10 mol of liquid water.

(g) + 13O

(g) → 8CO

(g) + 10H

O(l)

The Meaning of a Chemical Equation

An equation is a precise quantitative summary of a reaction. It indicates the ratios

in which the reactants react and the products form. This means that the chemical

equation shows the exact number of molecules (or atoms or ions) that react and

the exact number of product molecules (or atoms or ions) that are formed. For

correctly balanced equations, the total masses on both sides of the equation

(taking the coefﬁcients into account!) should be equal. For example, we can sum-

marize this quantitative information contained in the equation for the synthesis

of aspirin as follows:

Equation C

(s) + C

(l) → C

(s) + C

(l)

Coefﬁcients 1 mol + 1 mol → 1 mol + 1 mol

Molar mass of 138.118 g + 102.088 g → 180.154 g + 60.052 g

component

Total reactant mass =240.206 g Total product mass =240.206 g

Ideally, we would follow signiﬁcant-ﬁgure rules in the above calculations. We

have not done so here in order to make a point about the conservation of mass in

an equation.

3.6 Chemical Equations 107