Kelter P., Mosher M., Scott A. Chemistry. The Practical Science

Подождите немного. Документ загружается.

EXERCISE 2.2 Atomic Bookkeeping

Fill in the blanks for each neutral element in the following table, and write the ele-

mental symbols using nuclide notation.

First Thoughts

To ﬁll in our table, we will use the relationships that deﬁne the mass number and

atomic number for an element. Speciﬁcally, we recall that

A − Z = n

A glance at the periodic table will be helpful, because the name of the element indi-

cates the atomic number of the element. On the periodic table inside the front cover

of this book, we can verify that the atomic number of silicon is in fact 14. We know

that this is equal to the number of protons in atoms of the element. In the blanks for

molybdenum, we are asked to ﬁnd the number of protons and electrons present in

an atom of the neutral element. We are given the number of neutrons (n) and the

mass number (A), the sum of protons and neutrons. We can take the difference to

solve for the number of protons (Z):

A − n = Z

This is also equal to the number of electrons in the electrically neutral atom. The

key to ﬁlling in the blanks for krypton is to remember that the number of protons

equals the number of electrons in a neutral atom.

Solution

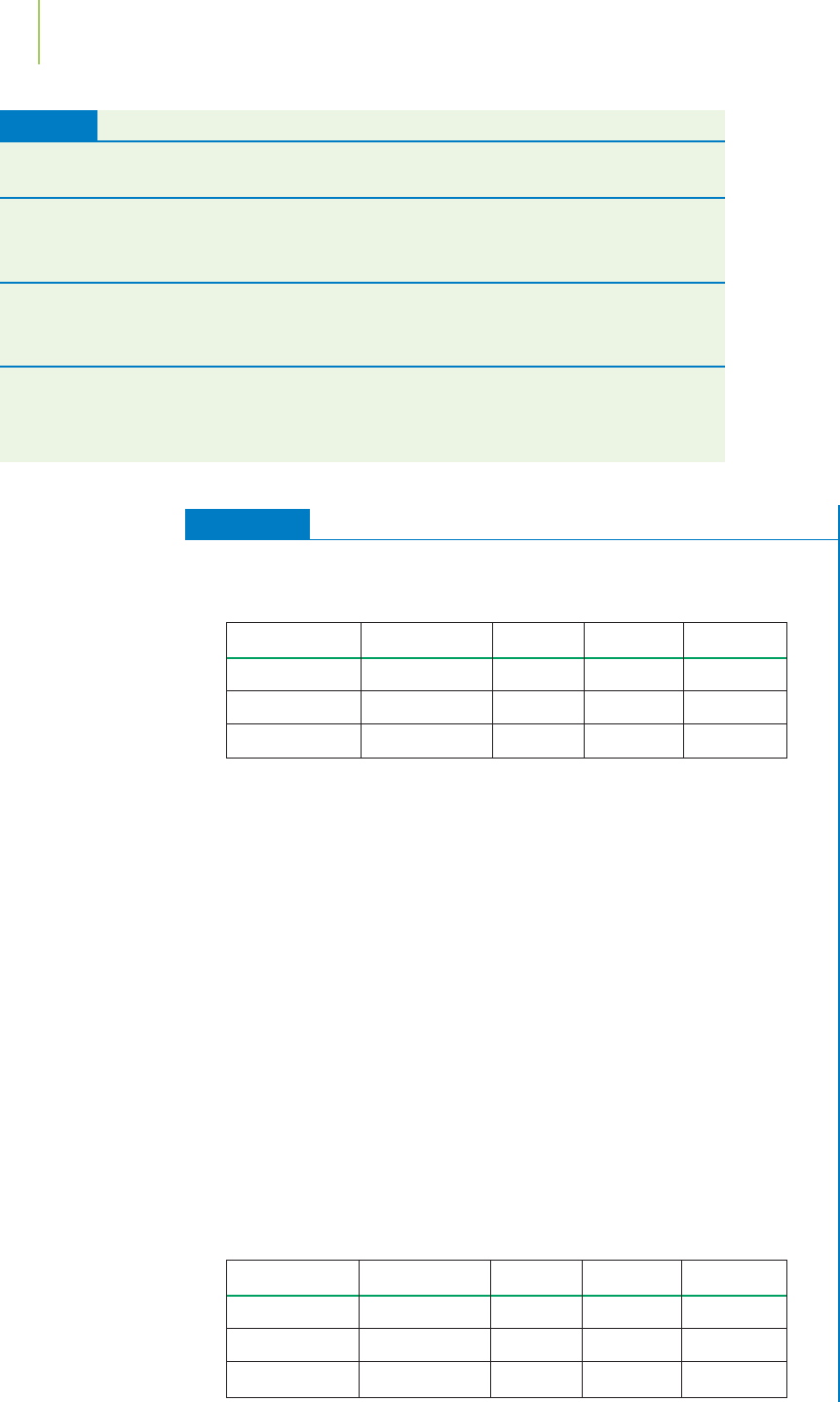
Element Mass Number Protons Neutrons Electrons

silicon 28 14 14 14

molybdenum 96 42 54 42

krypton 84 36 48 36

Element Mass Number Protons Neutrons Electrons

silicon 28 14

molybdenum 96 54

krypton 48 36

58 Chapter 2 Atoms: A Quest for Understanding

Some Isotopes of Hydrogen, Carbon, and Oxygen

Nuclide Relative Natural

Notation Abundance (%) Name of Isotope Protons Neutrons Electrons

H 99.985% hydrogen 1 0 1

H 0.015 deuterium 1 1 1

H10

−18

tritium 1 2 1

C 98.93 carbon-12 6 6 6

C 1.07 carbon-13 6 7 6

C2× 10

−10

carbon-14 6 8 6

O 99.762 oxygen-16 8 8 8

O 0.038 oxygen-17 8 9 8

O 0.200 oxygen-18 8 10 8

TABLE 2.4

Further Insights

As we go through the various numerical features of the elements, such as mass

number and numbers of protons, neutrons, and electrons, please keep in mind that

these numbers represent one of two ways in which we characterize the elements.

The other way, which ultimately led to the formation of the periodic table of the

elements, is via the physical and chemical characteristics of the elements.

PRACTICE 2.2

Indicate the number of protons, neutrons, and electrons in atoms of each of these

elements:

Carbon-11 Lithium-7 Phosphorus-31

See Problems 25, 26, 35–40, 45, and 46.

2.5 Atomic Mass

Plants and other organisms have a slightly greater preference for the lighter

isotopes of the carbon that they use as a raw material. When a plant absorbs car-

bon dioxide to make cell walls, it more efﬁciently uses the molecules that contain

the carbon-12 isotope than those that contain carbon-13 or carbon-14. The pref-

erence isn’t great at all, but the plant absorbs a slightly larger proportion of

carbon-12 than of the other carbon isotopes. When the organism dies, it leaves

behind some residue that is indicative of this preference. How does the scientist

in search of the origins of life determine the amount of carbon-12 versus the

amount of carbon-13 in a rock formation?

The distribution of isotopes in a sample of an element can be found using an

instrument called a

mass spectrometer. There are different kinds of mass spec-

trometers, but the simplest kind is illustrated in Figure 2.21. In the instrument, a

sample is vaporized and then converted into positive ions when a beam of fast-

moving electrons knocks some of the electrons out of the atoms of the sample.

The ions that are formed are accelerated by their attraction to charged plates.

Holes in these plates allow some of the ions to be projected through and into a

magnetic ﬁeld. The interaction between the charge on the ions and the magnetic

ﬁeld causes the ions to be deﬂected from their original path. The extent of this

deﬂection depends on the masses and charges of the ions. The more massive an ion

is, the less deﬂection it experiences, because of the greater momentum it possesses

when heading out in its original straight-line path (much as a very heavy adult

would not be blown so far off course by a ﬁerce,gusty wind as a small child would).

Some atoms have two of their electrons knocked away by the beam that

strikes them, converting them into cations with a +2 charge. These ions deﬂect

2.5 Atomic Mass 59

Sample

Positive

ions

Electron

beam

Sample is

vaporized

Accelerated

ion beam

Magnetic field

Detector

plate

Least

massive ions

Most

massive ions

Slits

FIGURE 2.21

The mass spectrometer separates ions by

exploiting their deﬂection to different

extents in a magnetic ﬁeld.

Application

Video Lesson: Mass

Spectrometry: Determining

Atomic Masses

60 Chapter 2 Atoms: A Quest for Understanding

100

35 36 37 38

Atomic weight (amu)

Relative intensity

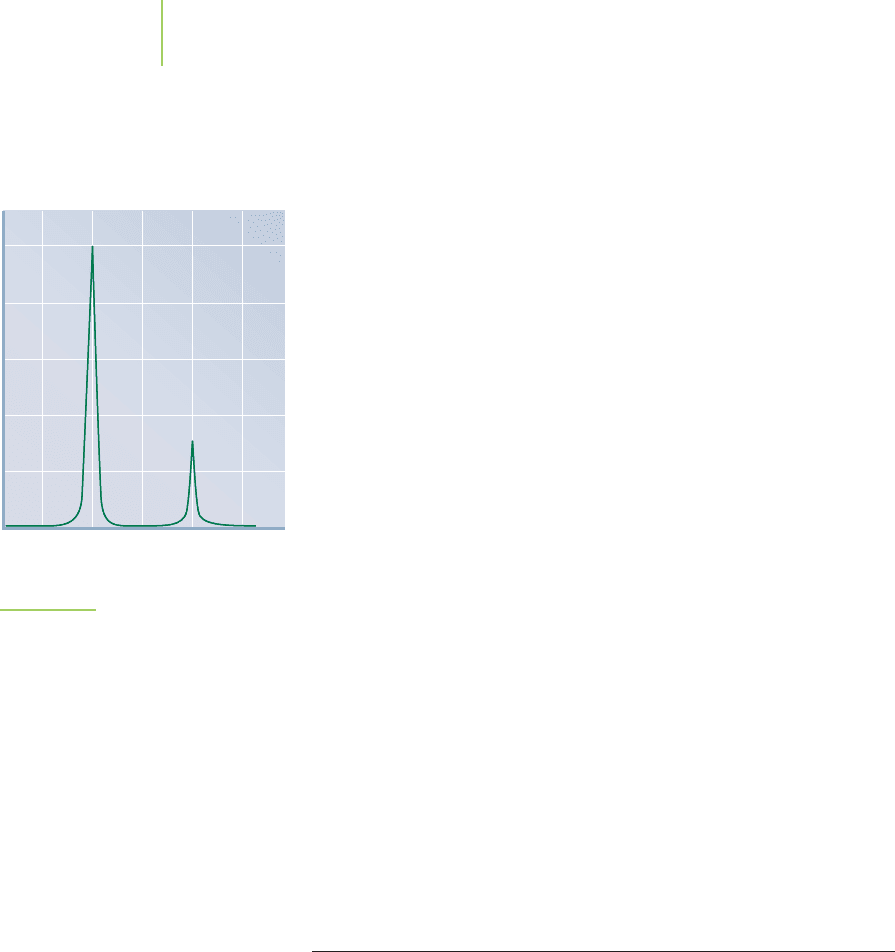
FIGURE 2.22

The mass spectrum of chlorine. From this

spectrum we can determine the relative

abundances of

CI (75.77%) and

(24.23%).

more than otherwise identical ions with a single positive charge because of the

greater interaction between their charge and the magnetic ﬁeld. Within a very

short distance, the original coherent beam of ions spreads out into beams of dis-

tinct ions, each with a different mass-to-charge ratio.

At the end of the mass spectrometer, the beams of ions are detected. The re-

sults are displayed in a

mass spectrum, as shown in Figure 2.22. Each line on the

spectrum indicates the relative quantity of the different ion beams that result

from the original sample. Using a standard that produces an ion beam with a

known mass, we can reproduce the scale on the bottom of the mass spectrum.

In much the same way, we use a standard to determine the masses of the

atoms in the periodic table. Which element is used as the standard? The most

abundant isotope of carbon,

C, is deﬁned as exactly 12 atomic mass units (amu).

C = 12.000000000 amu

An atomic mass unit, an arbitrary unit used to set the masses reported in the

periodic table, is currently deﬁned as follows:

1 amu = 1.66053873 × 10

−27

kg 1 kg = 6.02214198 × 10

amu

1 g = 6.02214198 × 10

amu

Strictly speaking, the amu is not an SI unit, but its use remains sufﬁciently com-

mon among scientists that we will use it in this textbook.

A detailed look at the mass of individual isotopes shows that they are typically

not integer values. That is, the isotope

Cu does not have a mass of exactly 63.

Only

C is deﬁned with an exact mass. The isotope

Cu has a mass number of 63

but a mass of 62.9296011 amu. The isotope

Mo has a mass of 95.9046789 amu.

Precise measurements have shown that neither a proton (roughly 1.0073 amu)

nor a neutron (roughly 1.0087 amu) has a mass of 1 amu. Therefore, the isotope

238

U, which has an atomic mass of 238.0508 amu, has an atomic mass lower than

the sum of the protons and neutrons, which have a total mass of 239.9418 amu,

as shown.

Mass of 92 individual protons of

238

= 92 × 1.0073 amu = 92.6716 amu

Mass of 146 individual neutrons of

238

= 146 × 1.0087 amu = 147.2702 amu

Total mass of individual protons and neutrons of

238

U = 239.9418 amu

Where did the rest of the mass go? When the nuclei of elements formed from

the individual neutrons and protons, some of the mass—a different amount for

each isotope of each element—was released as energy (see Section 5.7).

Unfortunately, the individual masses don’t translate accurately into masses

that we can measure for a macroscopic quantity of an element found on a labo-

ratory shelf. The presence of isotopes complicates the mass even more. To illus-

trate this, assume we have a bottle of carbon powder. What mass should we use

for the typical carbon atom found in this bottle, given that three different iso-

topes of carbon exist: carbon-12, carbon-13, and carbon-14? Fortunately, in na-

ture, the relative abundance of each isotope remains largely constant. In addition,

the relative natural abundances of each of the isotopes of the elements have been

determined by scientists using mass spectrometers. Knowing the percentages of

each of the isotopes (and their masses), scientists have calculated the weighted

average mass of each element, and that is the atomic mass listed for it in the

periodic table. For our bottle of carbon powder, we would use 12.011 amu as the

average mass.

To better understand the concept of weighted average, we can draw an

analogy to a student grade point average (GPA). Let’s look at an “A student” who

completed 10 credits of coursework in a semester. If 5 credits were A grades (4.0,

on a scale of 0.0 to 4.0), 3 credits were B (3.0), and 2 credits were C (2.0), then her

2.5 Atomic Mass 61

overall GPA would be the weighted average of the individual course grades. The

A grade has the greatest weight because fully half the credits were in that course.

The C grade would (thankfully) have the least weight, because that course repre-

sented only 20%, or 0.20, of the whole course load. The weighted average (here,

the GPA) would be

(0.50 × 4.0) + (0.30 × 3.0) + (0.20 × 2.0) = 3.3

contribution of: A grades B grades C grades

Does the answer make sense? Even though the student received one grade each of

A, B, and C, the A was present in much greater abundance—5 credits—than the B

or the C. It therefore makes sense that the GPA should be a little higher than 3.0,

a straight B average. We can use the same strategy to calculate the atomic mass of

an element. For example, mass spectrometry reveals what we have noted previ-

ously: that carbon-12 accounts for 98.93% of all carbon atoms. Carbon-13 makes

up 1.07% of the carbon atoms, and carbon-14’s contribution is negligible—

about 2

× 10

−

%. The average mass of carbon-12 is then

(12.00000 amu × 0.9893) + (13.00335 amu × 0.0107) = 12.011 amu

carbon-12 carbon-13

This agrees very nicely with the mass reported in the periodic table. The fact that

any sample of carbon has a mass greater than 12 reﬂects the increased mass con-

tribution made by the small proportion of carbon-13.

EXERCISE 2.3 Calculating the Atomic Mass Value

Naturally occurring chlorine is composed of two isotopes: chlorine-35 and

chlorine-37. As the spectrum shown in Figure 2.22 reveals, the lighter isotope is sub-

stantially more abundant than the heavier one. Use the relative abundances given in

the ﬁgure, along with the mass of each isotope, to calculate the atomic mass for

chlorine. Compare the mass you calculated with what is reported in the periodic

table of the elements.

First Thoughts

Analogies to common situations and experiences often help us visualize difﬁcult

concepts. Make use of the analogy to the grade point average that we discussed in

the text. It is precisely the same calculation, except that the abundance of each iso-

tope replaces the abundance of each grade.

Solution

Atomic mass = (34.968852 × 0.7577) + (36.965903 × 0.2423) = 35.45

There was more chlorine-35 than chlorine-37 present, so it makes sense that the

mass should be closer to 35 than to 37. This value agrees with the value reported in

the periodic table.

Further Insights

In addition to determining the masses of the isotopes of atoms, mass spectrometry

can be used to reveal the masses of large and small molecules and to identify the

presence of speciﬁc molecules. Some of the most important applications of mass

spectrometry are found in biology and medicine, where it can be used to determine

the masses of protein molecules or to analyze blood samples. One example—

showing how mass spectrometry plays a role in testing for illegal drug use in

athletics—is illustrated in Figure 2.23.

Isotope Mass Abundance

chlorine-35 34.968852 75.77%

chlorine-37 36.965903 24.23%

Application

62 Chapter 2 Atoms: A Quest for Understanding

FIGURE 2.23

Drugs of abuse can be separated using a

gas chromatograph and identiﬁed with

a mass spectrometer.

“Organic” foods are big business. Accord-

ing to the U.S. Department of Agriculture,

such foods are “(1) produced and handled without the

use of synthetic chemicals and (2) not produced on land

to which any prohibited substances, including synthetic

chemicals, have been applied during the 3 years immedi-

ately preceding the harvest of agricultural products.” Un-

like organic foods, many of the other foods that we con-

sume contain industrially produced chemical additives

that increase their shelf life, lend them a particular tex-

ture, or enhance their ﬂavor. Because of this, many con-

sumers want products that not only are organically grown

but also contain only natural additives. One useful way

of characterizing additives as natural or synthetic is by

looking at the atomic masses of their atoms with a mass

spectrometer.

The key to the analysis, pioneered by Randy Culp

and coworkers at the Center for Applied Isotope Studies

at the University of Georgia, is that synthetic ﬂavorings

are typically made from organic chemicals derived from

fossil fuels (“crude oil”). “Natural” ﬂavorings are made

from organic chemicals that have the same structure but

are derived from plants. Vanilla ﬂavoring, for example,

can either come from vanilla beans or be made by com-

bining individual compounds in an industrial process.

Other than the method by which they are made, there is

no difference between these two vanilla ﬂavorings. Or is

there?

Culp recognizes that plants were alive until they were

harvested for the ﬂavorings. Living things contain a con-

stant and small amount of radioactive

C, which de-

creases slowly after they die. Fossil fuels, composed of

formerly living materialthat has been chemically modiﬁed

for tens of millions of years, contain essentially no

NanoWorld / MacroWorld

Big effects of the very small: Flavor analysis

Measurement of the radiation that is particular to

indicates whether the chemicals in the ﬂavoring are from

fossil fuels or plants.

Once it is established that a ﬂavoring was prepared

from natural sources rather than fossil fuels, how can

Culp’s group tell whether the sample is made from a

vanilla bean, say, or synthetically prepared from com-

pounds derived from wood pulp? Each type of plant is

unique in the way in which it processes carbon in photo-

synthesis, so the ratio of

C to

C distinguishes differ-

ent sources of compounds. That is where a gas chromato-

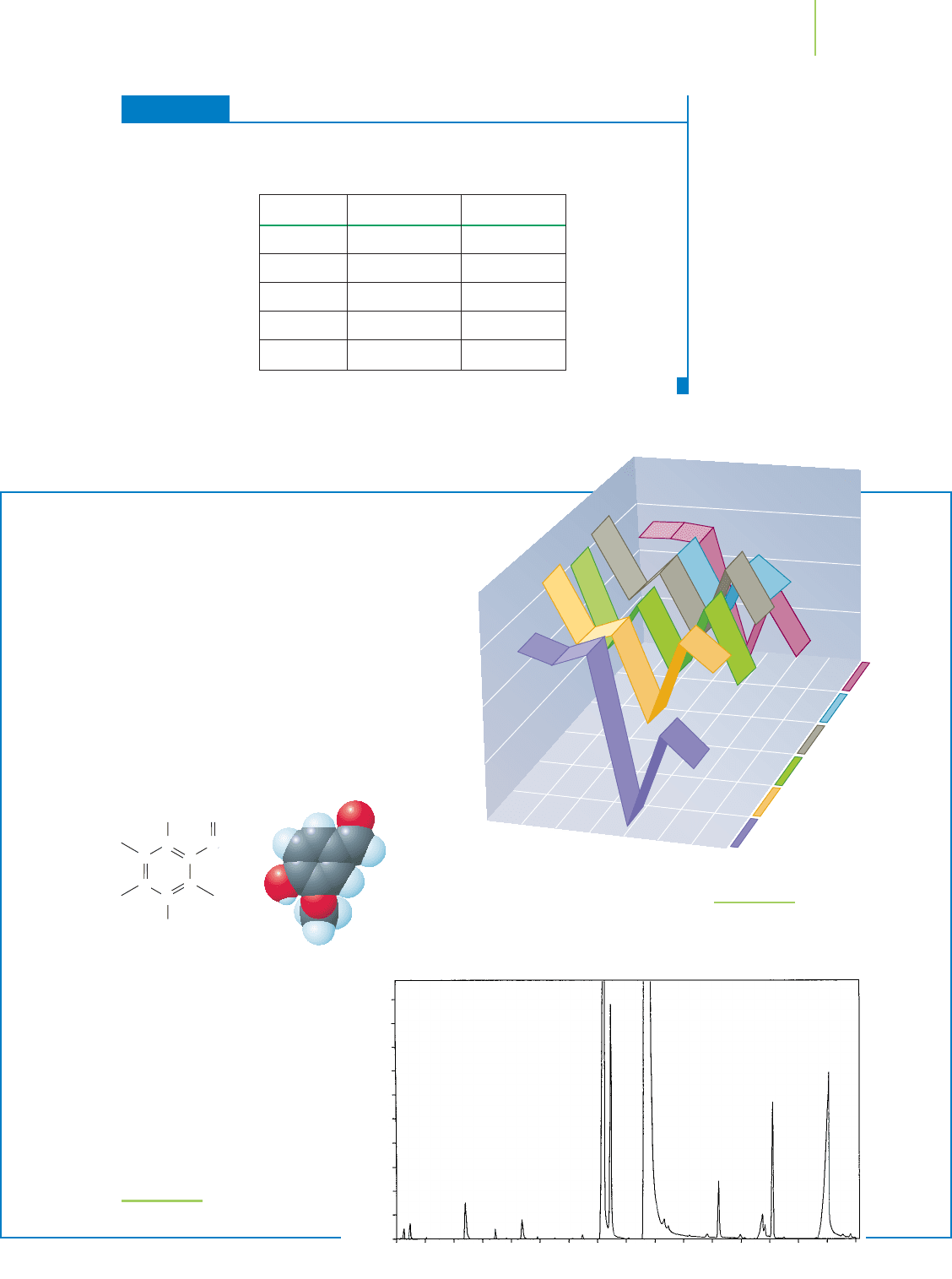
graph (GC) and mass spectrometer (MS), shown in

Figure 2.24, prove useful. The GC is a device that chemi-

cally separates the compounds in the vanilla ﬂavor on

the basis of their mass and structural properties. A sepa-

ration of a vanilla sample is shown in Figure 2.25. After

FIGURE 2.24

A modern gas chromatograph/mass spectrometer, a PerkinElmer

Clarus

500 GC/MS.

PRACTICE 2.3

Zinc has ﬁve isotopes, which have the masses (in amu) and the abundances given

below. What is the average atomic mass of zinc?

See Problems 51–56 and 98.

Isotope Mass Abundance

zinc-64 63.9296011 48.63%

zinc-66 65.9260368 27.90%

zinc-67 66.9271309 4.10%

zinc-68 67.9248476 18.75%

zinc-70 69.925325 0.62%

2.5 Atomic Mass 63

FIGURE 2.25

GC/MS analysis of vanilla sample.

C C

CHHO

C CH

OCH

Vanillin

separation, the individual components are con-

verted into carbon dioxide and fed to the MS,

where the ratio of

C to

C is measured.

Figure 2.26 shows the analysis of the

ratio of

C to

C of compounds in sev-

eral samples of vanilla. Note that one

compound, vanillin, is present in rela-

tively large amounts. It is a “character-

istic compound” of vanilla, and we

associate its smell with the product.

Peppermint, citrus, and other oils have

similar characteristic compounds.

–32

p-OH-Benzaldehyde

o-vanillin

Vanillin

Syringaldehyde

p-OH-Benzoic acid

Vanillic acid

–28

Tonga-5269

Mexico-6234

Mexico-6233

Comore-6232

Comore-6231

Comore-5271

–24

–20

–16

Delta Carbon-13

Component

Source

FIGURE 2.26

The ratio of

C to

C reveals the

origin of the sample.

5000

10000

15000

20000

25000

30000

ρ-hydroxy benzaldehyde

ρ-hydroxy benzoic acid

Vanillin

Vanillic acid

35000

40000

45000

50000

8 101214161820

Time (minutes)

Abundance

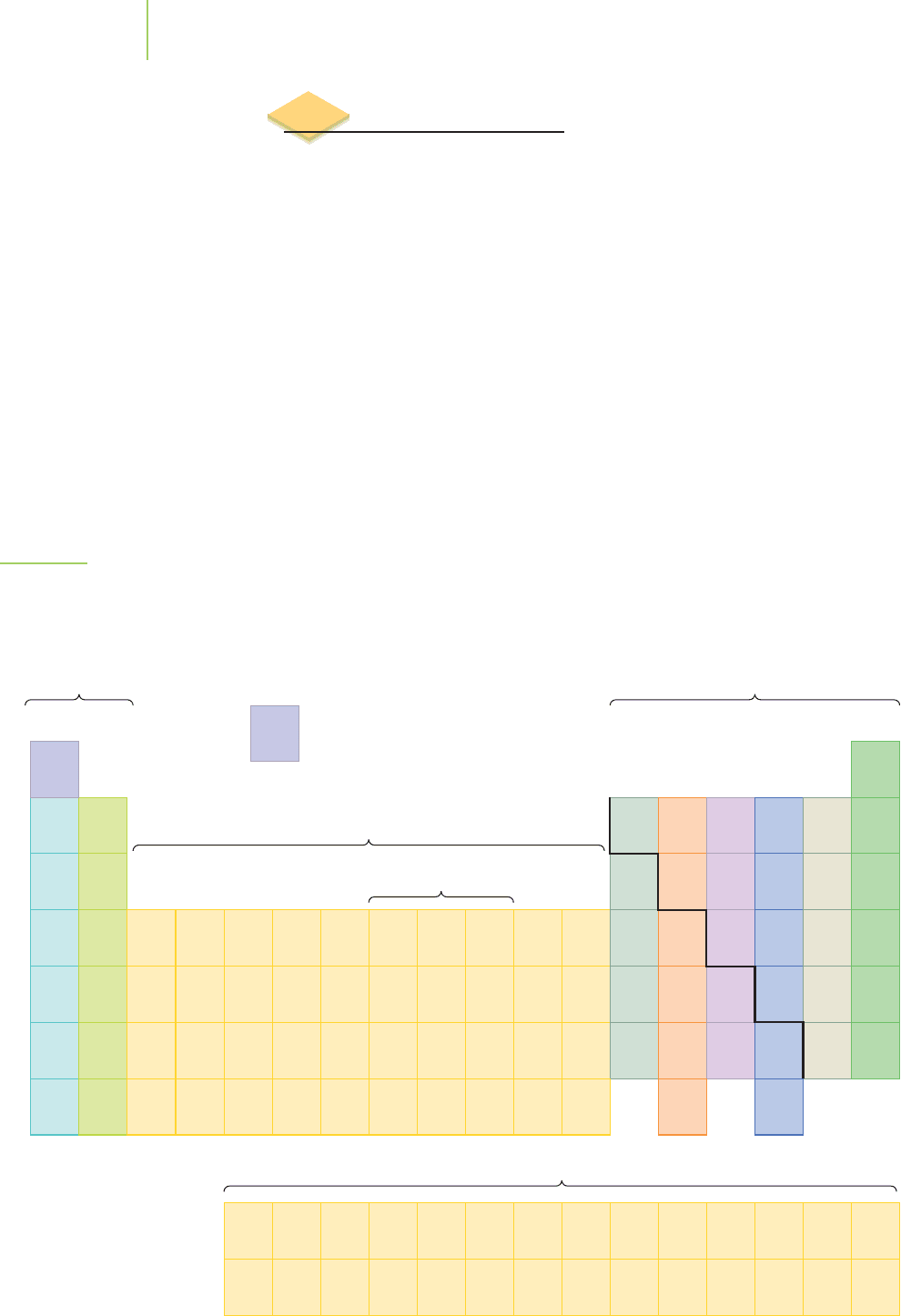
FIGURE 2.27

The elements are arranged in the

periodic table in columns that represent

similar properties. Elements with similar

properties are also color-coded.

64 Chapter 2 Atoms: A Quest for Understanding

2.6 The Periodic Table

The periodic table of the elements is the most signiﬁcant document summarizing

what we know about atoms. The table, shown in Figure 2.27 and on the inside

front cover of this book, is the reference chart that shows the hierarchy of atomic

structure. The layout of the table summarizes some of the most crucial ideas and

discoveries of chemistry.

The periodic table is arranged in

periods (rows) and groups (columns). If you

read from left to right along the ﬁrst period, then left to right along the second

period, and so on, you will ﬁnd the atomic numbers building up one proton at a

time. The atoms generally get heavier as you move along the periods. The table

seems to have a strange structure in places, with unexplained spaces we must

jump over as we read. There are excellent reasons for the shape of the table, and

we will discuss them in Chapter 6.

The arrangement of elements in the periodic table is linked to each element’s

chemical properties in ways that enable us to make many useful predictions. One

of the speciﬁc arrangements is indicated by the heavy stair-step line on the right-

hand side of the table. This line serves as the boundary between metal and non-

metal elements. The

metals, located to the left of the boundary, share common

characteristics. They are lustrous (shiny), malleable (can be shaped or bent), and

ductile (can be stretched into wires), and they act as conductors of heat and elec-

tricity. Many of these metals are commonplace in everyday life, such as iron (Fe),

the main component of steel; copper (Cu), used to make electric wiring; and the

silver (Ag) and gold (Au) used widely in jewelry.

1.00794

6.941

22.989770

39.0983

85.4678

132.90545

(223)

9.012182

24.3050

40.078

87.62

137.327

(226)

44.955910

88.90585

La*

138.9055

Ac**

(227)

47.867

91.224

178.49

104

(261)

50.9415

92.90638

180.9479

105

(262)

51.9961

95.94

183.84

106

(266)

54.938049

(98)

186.207

107

(264)

55.845

101.07

190.23

108

(277)

58.933200

102.90550

192.217

109

(268)

58.6934

106.42

195.078

110

(281)

111

Uuu

(272)

112

Uub

(285)

114

Uuq

(289)

116

Uuh

(292)

63.546

107.8682

196.96655

65.409

112.411

200.59

10.811

26.981538

69.723

114.818

204.3833

12.0107

28.0855

72.64

118.710

207.2

14.0067

30.973761

74.92160

121.760

208.98038

15.9994

32.065

78.96

127.60

(209)

18.9984032

35.453

79.904

126.90447

(210)

4.002602

20.1797

39.948

83.798

131.293

(222)

140.116

232.0381

140.90765

231.03588

144.24

238.02891

(145)

(237)

150.36

(244)

151.964

(243)

157.25

(247)

158.92534

(247)

162.500

(251)

164.93032

(252)

167.259

100

(257)

168.93421

101

(258)

173.04

102

(259)

174.967

103

(262)

Period

IIA

IIIB

IVB

VIB

VIIB

*Lanthanides

**Actinides

IIB

IIIA

IVA

VIA

VIIA

VIIIA

VIIIB

810

Transition metals

Atomic number

Symbol

Atomic weight

Inner transition metals

Main-group elements Main-group elements

2.6 The Periodic Table 65

The nonmetals, located to the right of the boundary, also share some common

properties that are quite different from those of the metals. Typically, they are not

lustrous, break easily, and act as insulators to heat and electricity. The nonmetals

are a much smaller set of elements than the metals, but they include some of the

most common elements found in living things. For example, the carbon (C),

hydrogen (H), oxygen (O), nitrogen (N), and phosphorus (P) atoms that form

DNA are all nonmetals.

The elements that form the stair-step boundary between metals and non-

metals are called

semimetals or metalloids. This group of elements exhibits some

properties associated with metals and other properties associated with non-

metals. Some of their properties are intermediate between the two. For example,

they are lustrous but are often brittle. The semimetal silicon (Si) is called a semi-

conductor because its ability to conduct electricity is part way between that of a

conductor and that of an insulator.

The elements are also located in another pattern that indicates similar prop-

erties (Figure 2.28). Each vertical column in the periodic table contains a group

of elements with similar chemical and physical properties—hence the name

group. For instance, the elements of a group may combine with other elements in

a certain way, or they may have similar abilities to conduct or not conduct elec-

tricity. All of the elements in Group VIIIA, for example, are very stable gases that

are unreactive except under extreme conditions. They are known as the

noble

gases

—noble being used in the sense of having regal behavior. They are often

referred to as the

inert gases, although for those in the lower part of the group,

this is not, strictly speaking, correct. The helium used to keep dirigibles (blimps)

aloft and the neon used in neon lighting tubes are two common examples

of noble gases. All of the elements in Group IA are highly reactive metals known

Metals.

Metalloids. The metalloids silicon and

boron have properties that are

intermediate to the metals (see above)

and the nonmetals (such as selenium).

Nonmetals.

Gold

Copper

Silver

Iron

Hydrogen

Nitrogen

Oxygen

Phosphorus

Carbon

Silicon

Boron

Selenium

FIGURE 2.28

The main-group, transition, and inner

transition elements.

66 Chapter 2 Atoms: A Quest for Understanding

La*

Ac**

104

105

106

107

108

109

110

111

Uuu

112

Uub

100

101

102

103

Period

IIA

IIIB IVB VB VIB VIIB

*Lanthanides

**Actinides

IB IIB

IIIA IVA VA VIA VIIA

VIIIA

VIIIB

Transition metals

Atomic number

Symbol

Inner transition metals

Main-group elements Main-group elements

as the alkali metals because they form compounds called alkalis when left in con-

tact with water. Table 2.5 summarizes the titles most commonly used for some of

the groups in the periodic table.

Elements in the A groups of the periodic table are historically known as the

main-group elements, and those in the B groups are called transition elements or

transition metals (Figure 2.28). There are two rows of elements separated from

the main table known as the inner transition elements. We will have much more to

say about the historical and chemical organization of the periodic table in future

chapters. At this point, however, we have the background to begin learning about

how the elements combine to form more complex structures, including compounds

and molecules.

Some Groups in the Periodic Table with Characteristic Names

Group Common Name Members

IA Alkali metals Li; Na; K; Rb; Cs; Fr

IIA Alkaline earth metals Be; Mg; Ca; Sr; Ba; Ra

IB Coinage metals Cu, Ag, Au

VIA Chalcogens O; S; Se; Te; Po

(“chalk formers”)

VIIA Halogens F; Cl; Br; I; At

(“salt formers”)

VIIIA Noble gases He; Ne; Ar; Kr; Xe; Rn

(inert gases; “do not react easily”)

TABLE 2.5

2.7 Ionic Compounds 67

2.7 Ionic Compounds

Chemical reactions consist of the rearrangement of atoms to make different sub-

stances. Although the nucleus of an atom remains unchanged in the course of a

chemical reaction, the number of electrons surrounding that nucleus can change.

When electrons are added to or subtracted from a neutral atom or group of

atoms, a charged species known as an ion forms. For example, the neutral cal-

cium-40 atom has 20 protons, 20 neutrons, and 20 electrons, and we denote this

using the nuclide notation

Ca. When calcium combines with oxygen, it loses

two electrons, which the oxygen atom gains. We can write the nuclide notation

for the resulting calcium ion, which now has 20 protons and only 18 electrons

(two more positive than negative charges) as

18 = 18 electrons = –18 charge

20 = 20 protons = +20 charge

Net charge = +2

Because we are typically interested only in the charge on the ion, and the number

of protons is implicit in the symbol (that is, calcium must have 20 protons if it is

to be called calcium), we simplify the notation even further and write Ca

. Using

the same simpliﬁed notation, we denote the oxygen ion, which contains 8 protons

and 10 electrons, as O

2−

EXERCISE 2.4 Ions

Fill in the numbers missing from the following table.

Solution

Symbol Protons Neutrons Electrons Charge

2−

16 16 18 −2

137

56 81 54 +2



17 20 18 1

Symbol Protons Neutrons Electrons Charge

2−

56 81 54



20 1