Грицюк С.Н., Мирзоева Е.В., Лысенко В.В. Математические методы и модели в экономике

Подождите немного. Документ загружается.

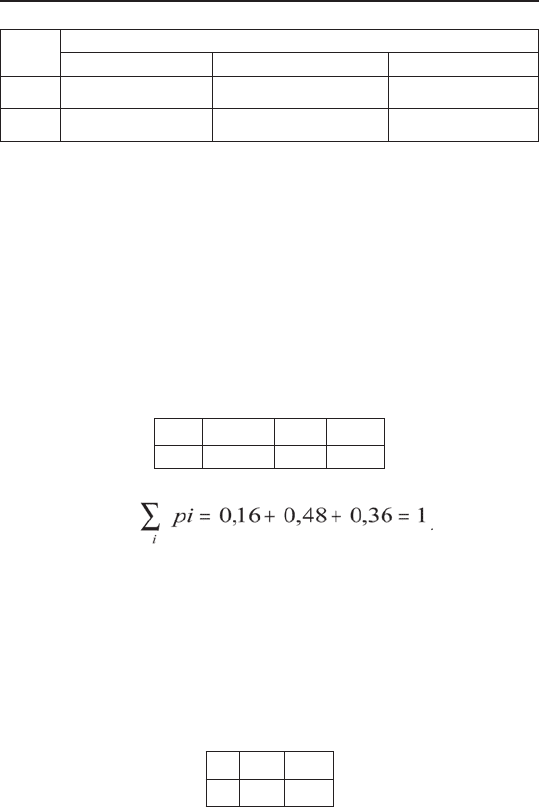
0

С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко

У Х

0,1 0,3 0,2

0,06 0,18 0,16

Решение

а) Сложив вероятности по столбцам, получим веро-

ятности возможных значений Х:

P(X

) = 0,1 + 0,06 = 0,16,

P(X

) = 0,3 + 0,18 = 0,48,

P(X

) = 0,2 + 0,16 = 0,36.

Напишем закон распределения составляющей х:

Х х

р 0,16 0,48 0,36

Контроль:

б) Сложив вероятности по строкам, получим веро-

ятности возможных значений У:

P(У

) = 0,1 + 0,3 + 0,2 = 0,6,

P(У

) = 0,06 + 0,18 + 0,16 = 0,4.

Закон распределения СВ У имеет вид:

у у

р 0,6 0,4

Еще закон распределения двумерной СВ может

быть задан аналитически, например в виде функции

распределения.

Функцией распределения вероятностей двумер-

ной СВ называют функцию F(x; y), определяющую

1

Математические методы и модели в экономике

для каждой пары чисел (x; y) вероятность того, что

X примет значение, меньшее x, и при этом

примет

значение, меньшее y: F(x; y) = P(X < x; Y < y).

Геометрически это равенство можно истолковать

так: F(x; y). Есть вероятность того, что случайная

точка(X; Y) попадет в бесконечный квадрант с вер-

шиной (x; y), расположенный левее и ниже этой вер-

шины.

Иногда вместо термина «функция распределения»

используют термин «интегральная функция».

Свойства функции распределения:

1. Значения функции распределения удовлетворяют

двойному неравенству: 0 ≤ F(x; y) ≤ 1.

2. Функция распределения есть неубывающая фун-

кция по каждому аргументу: F(x

; y) ≥ F(x

; y),

если x

> x

; F(x; y

) ≥ F(x; y

), если y

> y

3. Имеют место предельные соотношения: а) F(-;

y) = 0; б) F(x; -) = 0; в) F(-; -) = 0; г) F(;

) = 1.

4. При y =  функция распределения системы ста-

новится функцией распределения, составляющей

X: F(x; ) = F

(x).

5. При x =  функция распределения системы ста-

новится функцией распределения, составляющей

Y: F(; y) = F

(y); P(x

< X < x

; y

< Y <y

) =

= [F(x

; y

) – F(x

; y

)] – [F(x

; y

) – F(x

; y

)].

Используя функцию распределения, можно найти

вероятность попадания случайной точки в прямо-

угольник: x

< X < x

; y

< Y <y

2.2.3. Закон больших чисел.

Неравенство Чебышева

Как уже известно, нельзя заранее уверенно пред-

видеть, какое из возможных значений примет слу-

чайная величина в итоге испытания; это зависит от

многих случайных причин, учесть, которые невоз-

можно, казалось бы, поскольку о каждой случайной

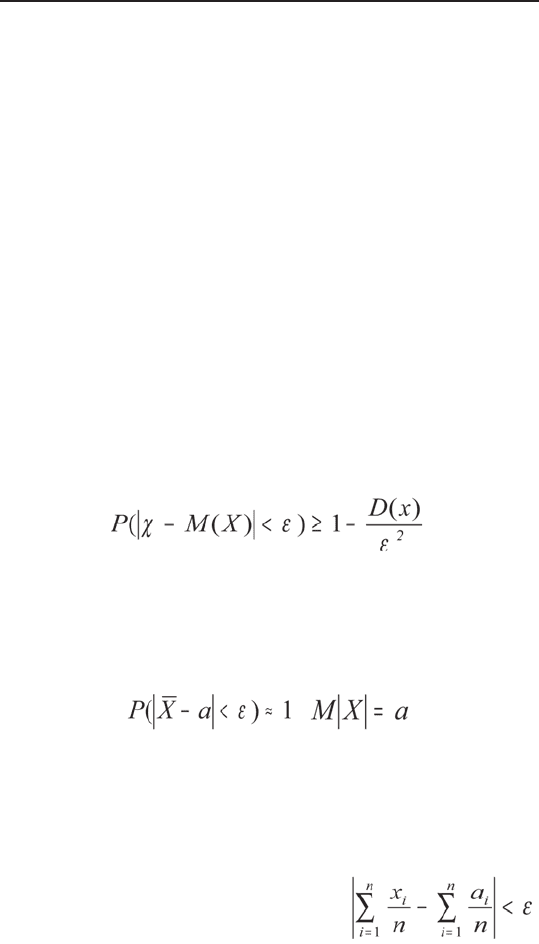
2

С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко

величине мы располагаем в этом случае весьма

скромными сведениями, то вряд ли можно устано-

вить закономерности поведения и суммы достаточ-

но большого числа случайных величин. На самом

деле это не так. Оказывается, что при некоторых,

сравнительно широких условиях, суммарное поведе-

ние достаточно большого числа случайных величин

почти утрачивает случайный характер и становится

закономерным.

Для практики очень важно знание условий, при вы-

полнении которых совокупное действие очень многих

случайных причин приводит к результату, почти не

зависящему от случая, так как позволяет предвидеть

ход явлений. Эти условия и указываются в теоремах,

носящих общее название — Закона больших чисел.

Неравенство Чебышева — вероятность того, что

отклонение случайной величины X от ее математичес-

кого ожидания по абсолютной величине меньше поло-

жительного числа ε, не меньше, чем 1 – D(x) | ε

Теорема Чебышева (частный случай). При неогра-

ниченном увеличении числа n независимых испытаний,

вероятность того, что средняя арифметическая наблю-

даемых значений сколь угодно мало и отличается от

материального ожидания, приблизительно равна 1:

Теорема Чебышева (общий случай). Если X

,...X

— независимые случайные величины с мате-

матическими ожиданиями a

, a

,...a

и дисперсиями

, D

,...D

, причем все дисперсии не превышают пос-

тоянной C, то как бы мало ни было положительное

число ε, вероятность неравенства

(2.52)



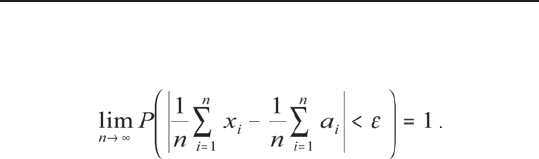
Математические методы и модели в экономике

будет как угодно близка к 1, если число случайной

величины будет достаточно велико, то есть

Сущность теоремы Чебышева. Среднее арифмети-

ческое достаточно большого числа независимых слу-

чайных величин (дисперсии которых равномерно ог-

раничены) утрачивает характер случайных величин.

На теореме Чебышева основан широко применяе-

мый в статистике выборочный метод, суть которого

состоит в том, что по сравнительно небольшой слу-

чайной выборке судят о всей совокупности (так назы-

ваемой генеральной совокупности) изучаемых объек-

тов. (Пример: количество кипы хлопка — небольшой

пучок из разных мест кипы — в кипе волокон больше,

чем в пучке, но и в пучке достаточно большое коли-

чество).

2.3. Методы и модели корреляционно-

регрессионного анализа

2.3.1. Общие сведения

Большинство явлений и процессов в экономике

находятся в постоянной взаимной и объективной все-

охватывающей связи. Исследование зависимостей и

взаимосвязей между объективно существующими яв-

лениями и процессами играет большую роль в эконо-

мике. Оно дает возможность глубже понять сложный

механизм причинно-следственных отношений между

явлениями. Для исследования интенсивности, вида и

формы зависимостей широко применяется корреляци-

онно-регрессионный анализ, который является мето-

дическим инструментарием при решении задач про-

гнозирования, планирования и анализа хозяйственной

деятельности предприятий.



С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко

Различают два вида зависимостей между экономи-

ческими явлениями и процессами:

•

функциональную;

•

стохастическую (вероятностную, статистическую).

В случае функциональной зависимости имеется

однозначное отображение множества А на множест-

во В. Множество А называют областью определения

функции, а множество В — множеством значений

функции.

Функциональная зависимость встречается редко.

В большинстве случаев функция (Y) или аргумент

(Х) — случайные величины. Х и Y подтверждены

действию случайных различных факторов, среди ко-

торых могут быть факторы, общие для двух случай-

ных величин.

Если на случайную величину Х действуют фак-

торы Z

, Z

, …, V

, V

, а на Y – Z

, Z

, V

… то

наличие двух общих факторов Z

и V

позволяет го-

ворить о вероятностной или статистической зависи-

мости между Х и Y.

Статистической называется зависимость меж-

ду случайными величинами, при которой изменение

одной из величин влечет за собой изменение закона

распределения другой величины.

В частном случае статистическая зависимость про-

является в том, что при изменении одной из величин

изменяется математическое ожидание другой. В таком

случае говорят о корреляции или корреляционной за-

висимости.

Статистическая зависимость проявляется только в

массовом процессе, при большом числе единиц сово-

купности.

В экономике приходится иметь дело со многими

явлениями, имеющими вероятностный характер. На-

пример, к числу случайных величин можно отнести:

стоимость продукции, доходы предприятия, межре-

монтный пробег автомобилей, время ремонта оборудо-

вания и т. д.



Математические методы и модели в экономике

Односторонняя вероятностная зависимость между

случайными величинами есть регрессия. Она устанав-

ливает соответствие между этими величинами.

Односторонняя стохастическая зависимость выра-

жается с помощью функции, которая называется рег-

рессией.

Виды регрессии:

1. Регрессия относительно числа переменных.

Простая регрессия — регрессия между двумя.

Множественная регрессия — это регрессия между

зависимой переменной у и несколькими объясняю-

щими переменными х

, х

, …, х

. Множественная

линейная регрессия имеет следующий вид:

У= а

+ а

+ …+ а

где: у — функция регрессии;

, х

, …, х

— независимые переменные;

, а

, …, а

— коэффициенты регрессии;

— свободный член уравнения;

n — число факторов, включаемых в модель.

2. Регрессия относительно формы зависимости:

•

линейная регрессия, выражаемая линейной функ-

цией;

•

нелинейная регрессия, выражаемая нелинейной

функцией.

3. В зависимости от характера регрессии различают

следующие ее виды:

•

положительную регрессию. Она имеет место, если

с увеличением (уменьшением) объясняющей пе-

ременной значения зависимой переменной также

соответственно увеличиваются (уменьшаются);

•

отрицательную регрессию. В этом случае с уве-

личением или уменьшением объясняющей пере-

менной зависимая переменная уменьшается или

увеличивается.

4. Относительно типа соединения явлений разли-

чают:

(2.53)



С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко

•

непосредственную регрессию. В этом случае зави-

симая и объясняющая переменные связаны непос-

редственно друг с другом;

•

косвенную регрессию. В этом случае объясняющая

переменная действует на зависимую через ряд

других переменных;

•

ложную регрессию. Она возникает при формаль-

ном подходе к исследуемым явлениям без уясне-

ния того, какие причины обуславливают данную

связь.

Регрессия тесно связана с корреляцией.

Корреляция в широком смысле слова означает

связь, соотношение между объективно существующи-

ми явлениями. Связи между явлениями могут быть

различны по силе.

Понятия «корреляция» и «регрессия» тесно связаны

между собой. В корреляционном анализе оценивает-

ся сила связи, а в регрессионном анализе исследуется

ее форма. Корреляция в широком смысле объединяет

корреляцию в узком смысле и регрессию.

Корреляция, как и регрессия, имеет различные

виды:

1. Относительно характера корреляции различают:

•

положительную;

•

отрицательную.

2. Относительно числа переменных —

•

простую;

•

множественную;

•

частную.

3. Относительно формы связи —

•

линейную;

•

нелинейную.

4. Относительно типа соединения —

•

непосредственную;

•

косвенную;

•

ложную.



Математические методы и модели в экономике

Любое причинное влияние может выражаться либо

функциональной, либо корреляционной связью. Но не

каждая функция или корреляция соответствует при-

чинной зависимости между явлениями. Поэтому тре-

буется обязательное исследование причинно-следс-

твенных связей.

Исследование корреляционных связей называется

корреляционным анализом, а исследование односто-

ронних стохастических зависимостей — регрессион-

ным анализом.

Корреляционный и регрессионный анализ имеют

свои задачи.

Задачи корреляционного анализа:

1. Измерение степени тесноты (связанности, силы),

формы и направления взаимосвязи между двумя и

более факторами (явлениями).

2. Отбор факторов, оказывающих наиболее сущес-

твенное влияние на результативный признак, на

основании измерения тесноты связи между явле-

ниями.

3. Обнаружение неизвестных причинных связей.

Корреляция непосредственно не выявляет при-

чинных связей между явлениями, но устанавли-

вает степень необходимости этих связей и досто-

верность суждений об их наличии. Причинный

характер связей выясняется с помощью логичес-

ки-профессиональных рассуждений, раскрываю-

щих механизм связей.

Задачи регрессионного анализа:

1. Установление формы зависимости (линейная

или нелинейная; положительная или отрица-

тельная и т. д.).

2. Определение функции регрессии и установление

влияния факторов на зависимую переменную.

Важно не только определить форму регрессии,

указать общую тенденцию изменения зависи-

мой переменной, но и выяснить, каково было бы



С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко

действие на зависимую переменную главных фак-

торов, если бы прочие не изменялись и если бы

были исключены случайные элементы. Для этого

делают функцию регрессии в виде математическо-

го уравнения того или иного типа.

3. Оценка неизвестных значений зависимой пере-

менной, то есть решение задач экстраполяции и

интерполяции. В ходе экстраполяции распростра-

няются тенденции, установленные в прошлом, на

будущий период. Экстраполяция широко исполь-

зуется в прогнозировании. В ходе интерполяции

определяют недостающие значения, соответству-

ющие моментам времени между известными мо-

ментами, то есть определяют значения зависимой

переменной внутри интервала заданных значений

факторов.

2.3.2. Линейная регрессия

Пусть задана система случайных величин Х и Y и

случайные величины Х и Y зависимы.

Представим одну из случайных величин как линей-

ную функцию другой случайной величины Х:

Y= g(x) = α + βx,

где α, β — параметры, которые подлежат опреде-

лению.

Эти параметры могут быть определены различны-

ми способами, наиболее часто используется метод на-

именьших квадратов (МНК).

Функцию g(x) называют наилучшим приближе-

нием в смысле МНК, если математическое ожидание

М[Y–g(x)]

принимает возможное наименьшее зна-

чение.

В этом случае функцию g(x) называют средней

квадратической регрессией Y на X.

(2.54)



Математические методы и модели в экономике

Рассмотрим определение параметров выбранного

уравнения прямой линии средней квадратической рег-

рессии по не сгруппированным данным. Пусть изучает-

ся система количественных признаков (Х ,Y), то есть

ведутся наблюдения за случайной двухмерной величи-

ной (Х , Y). Пусть в результате n наблюдений получе-

но n пар чисел (х

,у

), (х

, у

), …, (х

, y

Требуется по полученным данным найти выбороч-

ное уравнение прямой линии средней квадратической

регрессии:

Поскольку данные несгруппированные, то есть каж-

дая пара чисел встречается один раз, то можно перейти

от условной средней к переменной у. Угловой коэффи-

циент k обозначим через k = p и назовем ее выбороч-

ной оценкой коэффициента регрессии

Итак, требуется найти: y = px + b.

Очевидно, параметры p и b нужно подобрать так,

чтобы точки чисел (х

,у

), (х

, у

), …, (х

, y

), пост-

роенные по исходным данным, лежали как можно бли-

же к прямой (рис. 2.4).

Рис. 2.4. Динамика изменения признака Y

(2.55)