Грицюк С.Н., Мирзоева Е.В., Лысенко В.В. Математические методы и модели в экономике

Подождите немного. Документ загружается.

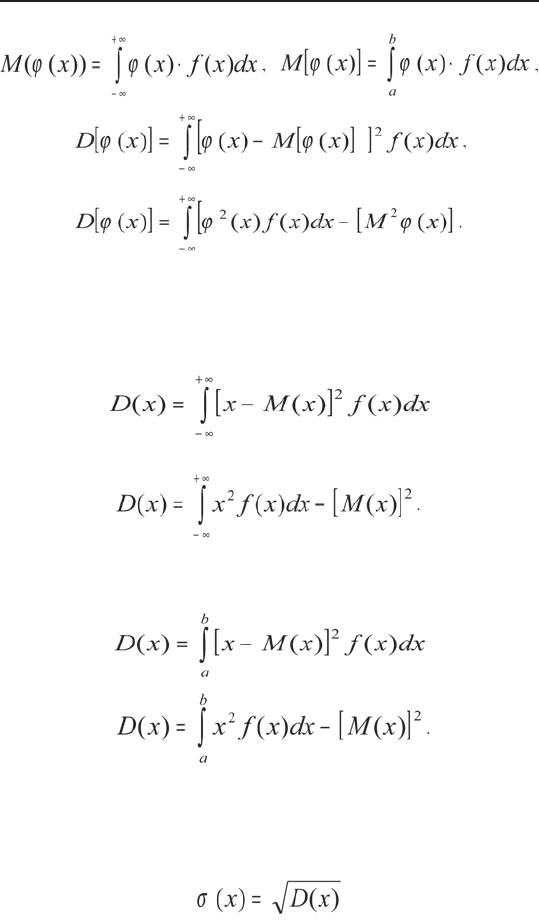
0

С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко

Все свойства математического ожидания, характер-

ные для ДСВ, сохраняются и для НСВ.

Дисперсия НСВ x, возможные значения которой

принадлежат всей оси Ox, определяются равенством

или равносильным равенством

В частном случае, если все возможные значения ве-

личины x принадлежат интервалу (a;b), то

или

Все свойства дисперсии, указанные выше для ДСВ,

сохраняются и для НСВ.

Среднее квадратическое отклонение НСВ опре-

деляется так же, как и для ДСВ:

(2.38)

(2.39)

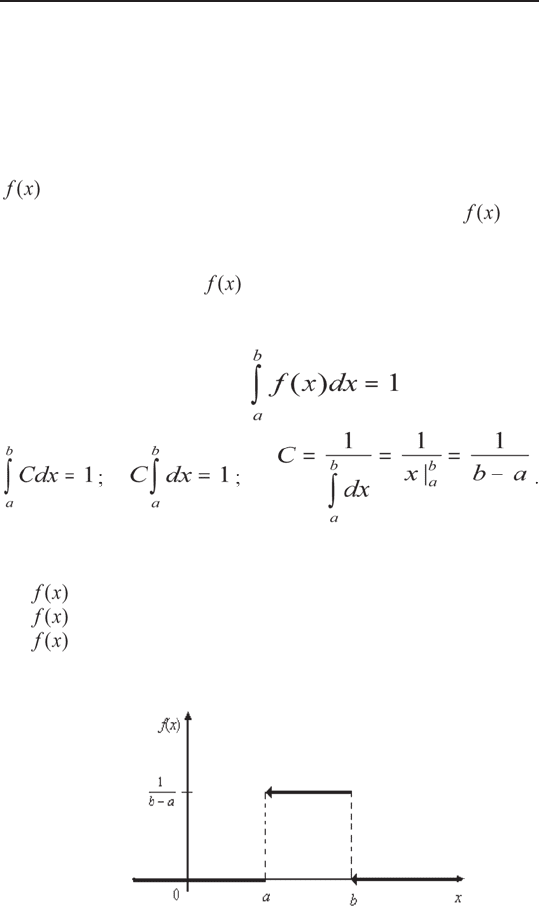
1

Математические методы и модели в экономике

Г. Равномерное распределение НСВ

Распределение вероятностей называют равномер-

ным, если на интервале, которому принадлежат все

возможные значения СВ, плотность распределения со-

храняет постоянное значение.

Найдем плотность равномерного распределения

, считая, что все возможные значения СВ заклю-

чены в интервале (a;b), на котором функция со-

храняет постоянное значение.

По условию, x не принимает значений вне интер-

вала (a;b), поэтому = 0 при x < a и x > b.

Найдем постоянную С. Так как все возможные зна-

чения СВ принадлежат интервалу (a;b), должно вы-

полняться соотношение или

Итак, искомая плотность вероятности равномерно-

го распределения:

= 0 при x ≤ a,

= 0 при a < x ≤ b,

= 0 при x > b.

График плотности равномерного распределения

имеет вид:

Рис. 2.1. Равномерное распределение

2

С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко

Нормальное распределение НСВ

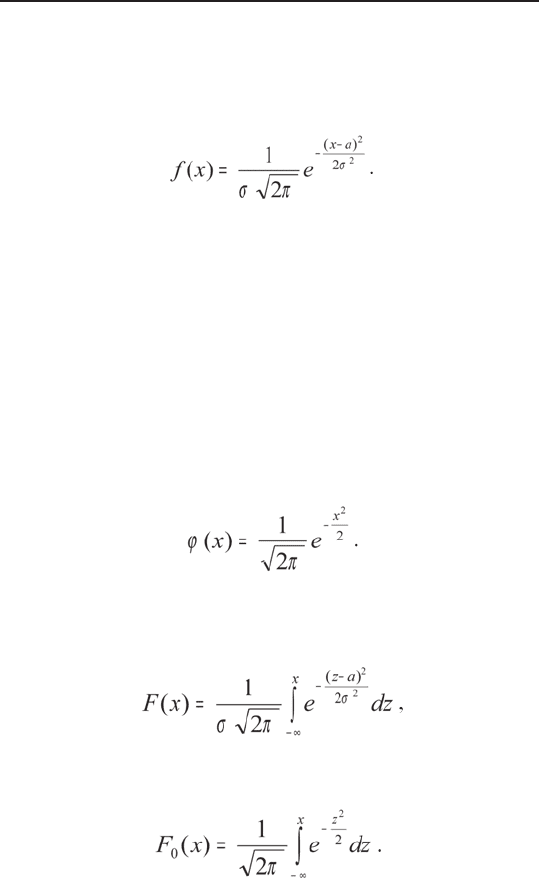
Нормальным называют распределение вероятнос-

тей непрерывной случайной величины, которое опи-

сывается плотностью

То есть нормальное распределение определяется

двумя параметрами: a и σ. Достаточно знать эти па-

раметры, чтобы задать нормальное распределение. Ве-

роятностный смысл этих параметров таков:

a — математическое ожидание,

σ — среднее квадратическое отклонение.

Общим называют нормальное распределение с про-

извольными параметрами a и σ (σ > 0).

Нормированным или стандартным называют нор-

мальное распределение с параметрами a = 0 и σ = 1.

Плотность стандартного нормального распределе-

ния имеет вид:

Значения этой функции занесены в таблицу (при-

ложение 1).

Функция F(x) общего нормального распределения

имеет вид:

а функция F

(x) стандартного нормального распре-

деления:

(2.40)

(2.41)

(2.42)

(2.43)



Математические методы и модели в экономике

Причем:

где

Ф(х) — функция Лапласа; ее значения также пред-

ставлены в таблице (приложение 2).

График плотности нормального распределения на-

зывают нормальной кривой (кривой Гаусса).

Свойства функции f(x):

1. Функция определена на всей числовой оси.

2. Функция положительна на всей области опреде-

ления, то есть кривая расположена над осью абс-

цисс Ох.

3. Прямая х = 0 является горизонтальной асимпто-

той, так как

4. Точка х = а является точкой максимума,

При x < a функция возрастает, при x > a функция

убывает.

5. График функции симметричен относительно пря-

мой х = а.

6. Точки и являются

точками перегиба.

7. График функции имеет вид:



С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко

Рис. 2.2. Нормальное распределение

Вероятность того, что непрерывная случайная ве-

личина Х, распределенная нормально, примет значе-

ние из интервала (α;β) равна

где Ф(х) — функция Лапласа.

Пример

Математическое ожидание и среднее квадратичес-

кое отклонение нормально распределенной случайной

величины Х соответственно равны 10 и 12. Найти ве-

роятность того, что в результате испытания Х примет

значение, заключенное в интервале (12, 14).

Решение

Воспользуемся формулой (6.10). Подставив α = 12,

β = 14, a = 10 и σ = 2 получим

По таблице приложения 2 находим: Ф(2) = 0,4772

и Ф(1) = 0,3413. Искомая вероятность Р(12<X<14) =

0,4772 – 0,3413 = 0,1359.

Вероятность того, что абсолютная величина откло-

нения нормально распределенной непрерывной случай-

ной величины меньше положительного числа δ, равна:

(2.44)



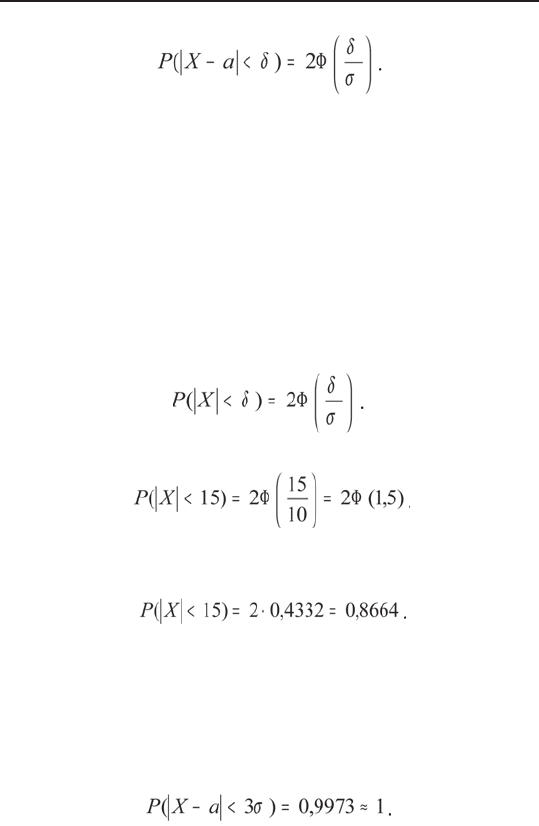
Математические методы и модели в экономике

Пример

Производится измерение диаметра вала без систе-

матических (одного знака) ошибок. Случайные ошиб-

ки измерения Х подчинены нормальному закону со

средним квадратическим отклонением σ = 10 мм. Най-

ти вероятность того, что измерение будет произведено

с ошибкой, не превосходящей по абсолютной величи-

не 15 мм.

Решение

Математическое ожидание случайных ошибок рав-

но нулю, поэтому формула (6.11) примет вид:

Подставив δ = 15 и σ = 10, получим:

По таблице приложения 2 находим: Ф(1,5) = 0,4332.

Искомая вероятность

Правило трех сигм

Если случайная величина распределена нормально,

то абсолютная величина ее отклонения от мате-

матического ожидания не превосходит утроенного

среднего квадратического отклонения, то есть

На практике это правило применяют так: если рас-

пределение изучаемой случайной величины неизвес-

тно, но условие (2.45) выполняется, то есть основа-

ние предполагать, что изучаемая случайная величина

(2.45)



С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко

распределена нормально; в противном случае она не

распределена нормально.

Показательное распределение

Показательным (экспоненциальным) называют

распределение вероятностей непрерывной случайной

величины Х, которое описывается плотностью:

где λ — постоянная положительная величина.

Функция распределения показательного закона:

Графики функций f(x) и F(x) имеют вид:

а) б)

Рис. 2.3.

а) показательное распределение

б) функция распределения показательного закона

Вероятность попадания в интервал (а;b) непрерыв-

ной случайной величины Х, распределенной по пока-

зательному закону, равна:

Значения функции е

-х

находятся по таблице при-

ложения 3.

(2.46)

(2.47)

(2.48)



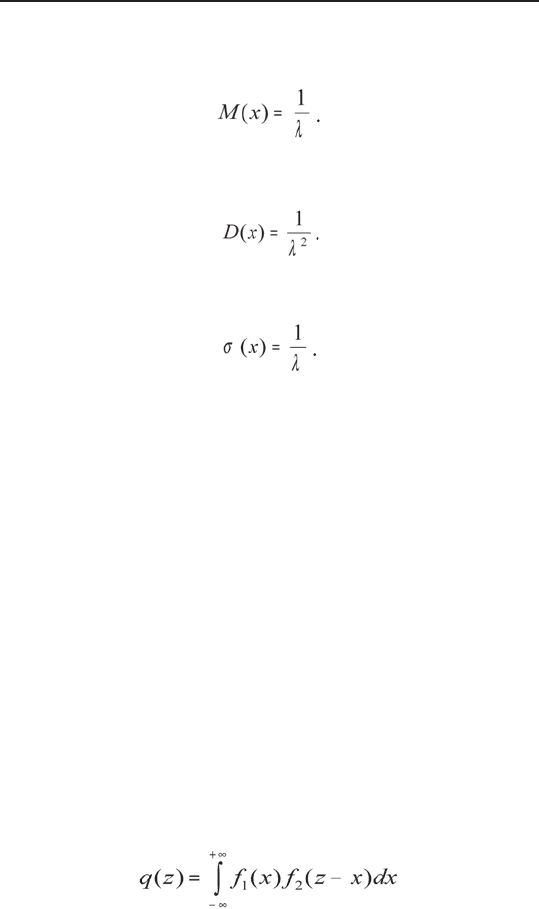
Математические методы и модели в экономике

Математическое ожидание показательно распреде-

ленной непрерывной случайной величины Х равно

Дисперсия показательно распределенной случай-

ной величины Х равна

Среднее квадратическое отклонение показательно

распределенной случайной величины Х равно

2.2.2. Многомерные случайные

величины

А. Функция двух случайных аргументов

Если каждой паре возможных значений случайных

величин Х и У соответствует одно возможное значение

случайной величины Z, то Z называют функцией двух

случайных аргументов Х и У и пишут Z = ϕ(X,У)

Если Х и У — дискретные независимые СВ, то для

того, чтобы найти распределение функции Z = X + У,

надо найти все возможные значения Z, для чего доста-

точно сложить каждое значение X со всеми возможны-

ми значениями У; вероятности найденных возможных

значений Z равны произведениям вероятностей скла-

дываемых значений X и У.

Если Х и У — непрерывные независимые СВ, то

плотность распределения q(z), суммы Z = X + У (при

условии, что плотность распределения хотя бы одного

из аргументов задана в интервале (– ; + ) (одной

формулой), может быть найдена по формуле

(2.49)

(2.50)

(2.51)



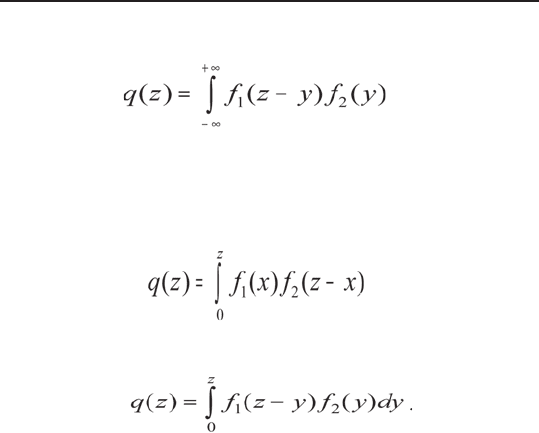
С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко

либо по равносильной формуле

dy,

где f

, f

— плотности распределения аргументов.

Если возможные значения аргументов неотрица-

тельны, то плотность распределения q(z) величины

Z = X + У находят по формуле:

dх,

либо по равносильной формуле:

Закон распределения двумерной случайной

величины

Двумерной называют СВ(Х, У), возможные значе-

ния которой есть пары чисел (х, у). Составляющие Х

и У, рассматриваемые одновременно, образуют систе-

му двух случайных величин.

Двумерную величину геометрически можно истол-

ковать как случайную точку М (Х, У) на плоскости

ХО у либо как случайный вектор ОМ.

Дискретной называют двумерную величину, со-

ставляющие которой дискретны.

Непрерывной называют двумерную величину, со-

ставляющие которой непрерывны.

Законом распределения вероятностей двумерной

СВ называют соответствие между возможными значе-

ниями и их вероятностями.

Законом распределения вероятностей двойной дву-

мерной СВ обычно задается в виде таблицы с двойным

входом.



Математические методы и модели в экономике

У Х

… X

p(x

, y

) p(x

, y

) … p(x

, y

)

… … … … … … …

p(x

, y

) p(x

, y

) … p(x

, y

) … p(x

, y

)

… … … … … … …

p(x

, y

) p(x

, y

) … p(x

, y

) … p(x

, y

)

Первая строка таблицы содержит все возможные

значения, составляющие X, а первый столбец — все

возможные значения, составляющие У. В клетке, сто-

ящей на пересечении «столбца x

» и «строки y

», ука-

зана вероятность p(x

, y

), того что двумерная случай-

ная величина примет значение p(x

, y

Так как события

образуют полную группу, то сумма вероятностей, по-

мещенных во всех клетках таблицы, равна 1.

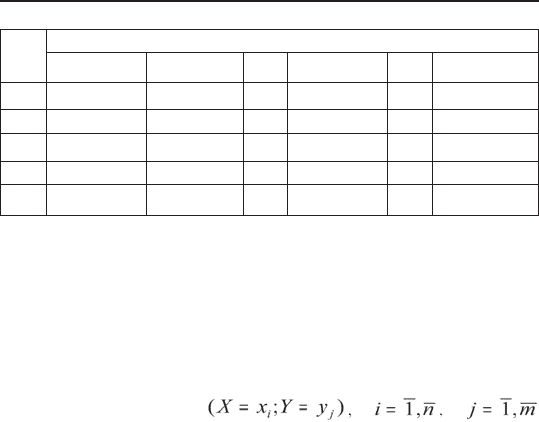
Зная закон распределения двумерной ДСВ, можно

найти законы распределения каждой из составляющих.

Действительно, например, события (X = x

; Y = y

(X = x

; Y = y

),..., (X = x

; Y = y

) — несовместны, по-

этому вероятность p(x

), того, что X примет значение

, по теореме сложения такова:

p(x

) = p(x

, y

) + p(x

, y

) + ... + p(x

, y

Таким образом, вероятность того, что X примет

значение X

, равна сумме вероятностей «столбца x

».

В общем случае, для того, чтобы найти вероятность

P = (X = x

), надо просуммировать вероятности стол-

бца x

. Аналогично, сложив вероятности «строки y

»,

получим вероятность P = (У = y

Пример

Найти законы распределения составляющих дву-

мерной СВ, заданной законом распределения.