Годфри Д. Теория упругости и пластичности
Подождите немного. Документ загружается.


8
которой
содержится
ненапряж
енное
отверстие.
Для
этого
случая
Хо
дж
*
получил
следующие
перемещения
при
а
-<
r
-<
R
а
также
обобщил
решение
па
случай,
когда
учитывается
ynроч
вение.
94.
ЦИЛИНДРИЧЕСКАЯ
ПО
Л
ОСТЬ
ПОД
ДЕЙСТВИЕМ
НЕСИММЕТРИЧНОЙ
НАГРУЗКИ
ОДНО
из
немноги
х
имеющихся
решений
упруго-пластич
ской
задачи,
не
упрощенной
высо.коЙ
степенью
симметрии,
было
по
л
у
ч
но
ГаJIИНЫМ
**.
Тело
с
цилиндрич
ской
полостью
подверга
тел
действию
растягивающих
сил
T
1
и
Т
2
11
двух
взаимно
перпевдп
кулярных
ваправлениях
и
в
пр
дположевии
условий
DЛОСНОЙ
де
формации
определяются
форма
упруго-пластичеекого
1\овтура
и
комп
оненты
напряжения
в
Dластич
ской
и
упругой
областях
при
не.которых
значениях
1\
и
Т
2
•
Кроме
того,
можно
пол
'lИть
давле
ние
р,
действующее
по
}{ОВТУРУ
полости,
прич
м
три
величины
T
L
Т
2
И
Р
подобраны
так,
что
пластическая
область
полвостью
онру
жает
отверстие.
Насколько
нам
и
звестно,
в
настоящее
время
н
е т
р
е
шения
для
случая
одного
растягива
ющего
УСИJlИЯ
T
1
,
когда
д
в
е
пластичес/{и
области
возникают
в
точках
А
максимальной
I\OU-
центрации
напряжений
(рис.
135).
Для
напряженного
состояния
в
пластической
области
по
Га
J
JИВУ
напряжения;:;:
и
ее
принимают
вид
(Х
П
.6)
и
такое
напряж
енн
ое
сост
ояние
может
быть
получено
с
помощью
бигармонической
функ
ции
напряжений
или
компле.кеных
потенциалов.
Для
состоя
нин
плоской
деформации
приняли
'Ф
=
~
+
iYz
=
О.
Таким
образ
ом
при
отсутствии
объемной
силы
уравнение
равновесия
(VI.7)
при
обретает
вид:
и удов л
етворя
'
тся:
при
д~
+
дФ
=
О
дl.
az
д
Р
= az '
дР
ф
=
-
-
d~
,
•
Р.
н
о
d g
е,
1.
А.
рр.
Mech., 1953,
р
.
530 .
(ХII
.
26
)
(ХП
.
27
)
••
Л.
А
.
Г
а
л
и
н.
Пространственвые
контаКТllые
вадачи
теории
YlIPY
-
гости
ДЛЯ
штампа
КРУГОВОЙ
формы
в
плане.
«ПРllli
лаДRая:
мате
fатика
и
{8-
хаВИRа»,
т.
10,
сТр.
365, 194
6.
250

где
F -
ФУНКЦИЯ
от
z
и
z .
Так
как
комбинация
напряжений
е
-
вещ
ственная
величина,
можем
принять
iJF
- -
=
---а;-
=
2
1
<р'
(z)
+
<р'
(z)
}.
(ХII.28)
Оп(
да
2 =
О,
что
определяет
напряж
нное
состояние
.
Если
бы
ВОС
.
польэовались
функциями
напряжения
Эри
(см.
56.
Ф
ункция
напряжений
Эри),
то
из
(VI.162)
2
(д
2
Х
+
д
З
Х
)
= V
4
X =
О
.
дх
2
д
у
2
ТаJ<ИМ
образом
напряженное
состояние,
полученное
из
(Х
Н
.27)
и
(ХII
.28),
было
бы
«бигармоничеСJ\ИМ».
Интегрирование
(ХII
.28)
приnодит
к
следующему
уравненюо
F = 2 (
<p(z)
+ z
(p
' (z) +
1j)(z)
J,
а.
и
з
(ХII.27)
ф
= - 2
{z
(j)"
(z) +
'Р'
(z»
).
(Х
Н.
29)
ЛеГJ<О
убедиться,
что
э
ти
уравнения
согласуются
с
(VI.25)
и
(VI.26),
но
так
IЩJ<
мы
им
ем дело
с
пластическим
СОСТОЯ
ни
м,
получение
номпонентов
перем
щения,
выраженных
через
комплеI<сные
потен
циалы,
весьма
затру
д
нено.
В
дальнейшем
нас
будут
интересовать
ТОЛЬКО
компоненты
напряжения,
поэтому
для
удобства
упростим
полученные
уравнения,
примем
<р'
(z) =
а
(z),
,р'
(z)
=
~
(z).
(ХН
.
ЗО)
С
л
довательпо,
= 2 (
a(z)
+
a(z)
J; }
ф
= - 2\
za
'
(z)
+
~
(z)J.
(ХII
.
З1)
Примевяя
такой
подход
J\
нашей
задаче,
будем
обозначать
индек
сом
1
величИJlЫ,
относящиеся
J\
пластичеСI<ОЙ
области,
и
ивдеJ\СОМ
2 -
к
упругой
области.
В
пластической
области
напряженное
с
остояние
(ХII.16)
приводит
к
следующим
комбинация
1
e~
= -
2р
+
2k
(1 +
2ln
-
;-)
Ф~
= - 2k,
)
(Х
II
.З2)
которые
получим
из
(ХII.31),
положив
~(z)
=
А
+
Blnz,
~l(Z)
=
О,
(ХII.33)
1 1
где
А
= - 2
Р
+
Z-k(
1 - 21na);
B
=k.
j
(ХII
.
34)
251

В
данном
случае
Галин
предлагает
найти
!,омплексные
потенци
алы
~
(z),
~2
(z)
В
упругой
области,
которые
даю'l'
правильные
ус
ловия
на
бесконечности,
а
таI<же
принимает
J<омбивацuи
напряже
ний
8'
и
Ф'
непрерывными
по
упруго-пластическому
КОНТУРУ_
Одвано
этот
КОВТУР
является
одним
из
неизвествых
в
задаче
ri
т
должен
определяться
одновременно
t l
t
J{ОМDлеI<СНЫМИ
потенциалаМII.
Это
дс-
у
лается
с
помощью
конфорыного
пр
е-
А
Упругая
образования,
при
котором
упруго-плас
Т,
--+-f-=jJ
' -'-JI---J.o.:.
ТИ'IeСКИЙ
I,ORTYP
L
(рис.
135)
пр
обра-
зуется
в
едини'lВУ1О
окружвость
у
В
комплексной
плоскости
~,
а
внешняя
L
по
отношению}{
этому
контуру
область
во
внешнIOЮ
об
ла
сть
ОJ<РУЖВОСТИ
у.
В
соответствии
с
эт
им примем
Р
ис
.
135.
(
1')
,.
йl
й:
(XII 35)
z=z.,
=c"
+T+-V+
... , .
n
позже
найдем
коэффицпевты,
ноторы
уДов
IО
ТВО
РЯЮТ
приn
еде
в
ные
выше
условия.
Из
(ХII.31)
и
(VI.67)
н
айдем
8'
=2I
et(
z)+
a{z»
); ]
Ф
'=
-2{za'(z) + :
~(
z
)}.
(ХII
.
36)
в
плоскости
6'
=
2
1
a(~)
+
a(~H;
(ХН.
37)
Ф'
= - 2
{z
(ё)
~'~)
+
-;
(
~
~
(б}
.
z'
(~)
z
(
~)
(ХII
.3
)
Для
того,
чтобы
~
(~)
и
~::
Ш
давали
непрерывность
напряжеНЮI
по
контуру
L,
потребуем
6~
= 8;,
Ф~
=
Ф~
на
О-а
=
1.
(ХП.39
)
Первое
из
этих
уравнений
удовлетворяется
при
~
Ш
=
А
+
В
ln
%
~~)
,
(ХП.40)
где,
как
можно
видеть,
8'
непрерывна
при
~
=
а
=
~
на
у.
Под
а
ставляя
это в
(ХН.38),
получи
f
Ф
= _ 2
{k
-
.!!...
z
ю
+
:.
(
~
1\ ("))
(ХIl
.4
1
)
2
~
z'
ю
t
(~)
1"
•
.,
,

п
для
непрерывности
Ф;
величина
Ф;
должна
быть
равной
-2k
на
са
=
1.
Поэтому
crримем
k
~(+)
~2
(с)
= - z'
(
~)
.
(ХII.42
)
Теперь
необхо
д
имо
убеДИТЬС
I1
в
том,
что
условия
удовлетворяются
на
бесконе'Шости.
Эти
ус
овия
требуют
I
zl
00
, 82
-+
Т
1
+
Т
2
,
Ф
2
-+
Т
1
-
Т
2
•
Таким
образом
па
преобразовани:е
(ХII.З5)
накла
дывается
ж
е
стко
е
огр
аниче
ние.
При
I z I
-+
00,
I
~
I
00
и
z =
c~,
так
'IТО
условие
для
2
с
учетом
(ХII.37)
требует,
чтобы
4(А
+
В
10
с)
=
Т
1
+
Т
2
•
Из
(ХII.З4)
(ХII.4З)
Из
(Х
II.З1)
на
ходим:
ф~
= - 2
{z
(С)
~
(~)
+~.
(~)}
= - 2 [
_'!.
(~
(k
~
~)
-~)
+
- z'
(~)
- z'
(~)
z
(~)
~
+
~
z
_(
т)
] = _
2k
[ :
(~)
_
~
:
(~]
+
~
%
~
*")
].
,.
:'
Ю
::
Ю
~
'1.'
(~)
~
z'
(~)
Исследуя
это
выра
жение,
I.;огда
I
~
I
-+
00,
н
аидем,
что
первые
два
()твошевия
стремятся
к
~/~
а
третье
стремится
J{
беСI(онечности,
если
lln =
о,
n >
2,
в
противном
случ
ае
оно
стремится
к
а, /
с
и
тог
ца
(ХII.44
)
СЛlщует
за
r
ет
и
ть,
что
:это
решение
сво
дится
к
уже
рассмотренным
СИ.1М
тричны
м
случанм,
если
:
Т
1
=
Т
2
=
Т
и р
=
о,
11
.3
(Х
П
.
44)
a
t
=
0,
тэl(
что
Z =
c~.
Поэтом
у
упруrо-пластический
КОН
'Х'ур
буд
т
ОI{РУЖНОСТЬЮ
С
ра
диу
сом
с,
веЛИЧJШа
которого,
получев
ная
и
(ХII.43),
согласуется
с
(Х
II
.22):
T
1
=
Т
2
=
О
тогда
свова
~
=
о:и
(ХII.43)
согласуется
С
(ХII.18),
когда
Ь
00
.
В
общем
слу
ч
ае
ра
внения
(ХII.4З)
и
(ХII.44)
опред
ел
яю
т
а
1
и
С,
а
преобразоваю[с
свод
ится
I{
следующему:
z=c~+~
.
(ХII.45)
Откуда
видно
что
L
есть
ЗЛЛИIIС
с
по
лу
осяьш
С
+
а
1
и
с
-
а,.
Для
того,
ч
тоб
ы
;mл
ипс
полпостыo
окружал
круглое
от
в
ерстие,
необхоДJIМО,
чтобы
при
Т
2
> T
1
,
С
-
l1t
:>-
а
плп
при
T
1
>
Т!
С
+
+
~
:>-
а.
Это
приводит
к
неравенству
5,---,-
--,-
'1
1-
---1--
3
т,/к
Р
ис.
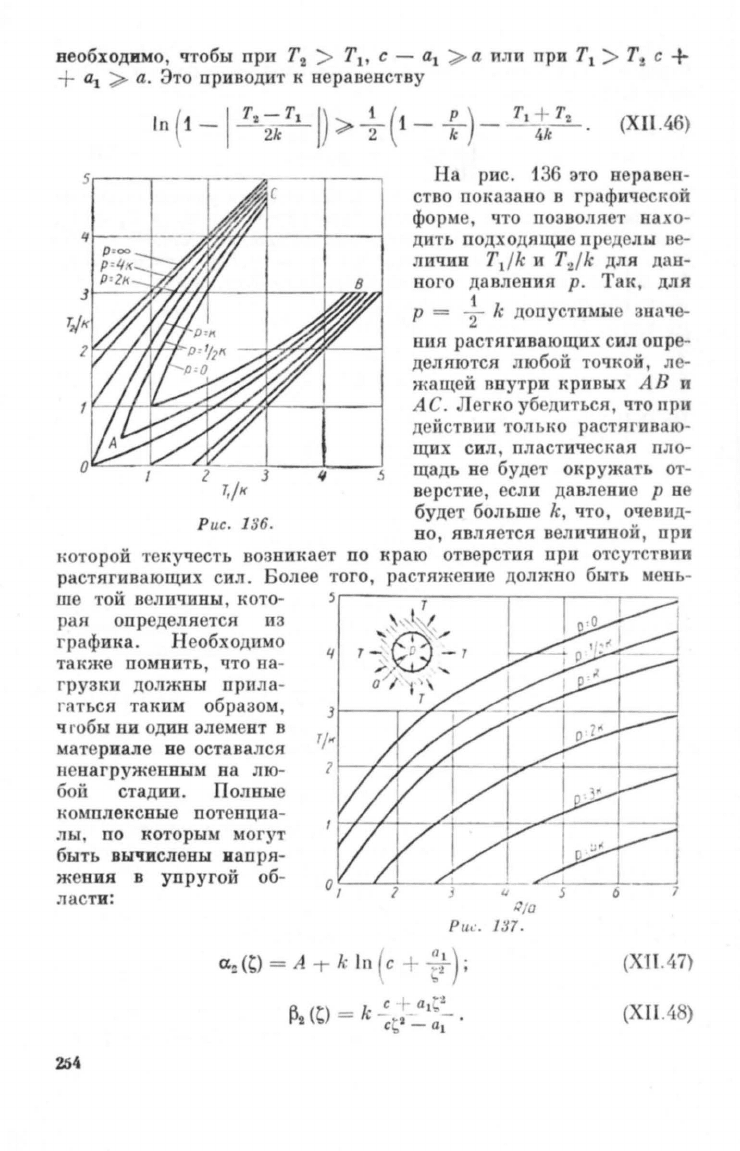
136.
На
рис.
136
ЭТО
иеравеп
ство
показано
в
графичесrtой
форм
,
что
позволяет
нахо
ДИТЬ
подходящие
пр
еде
лы
11
-
личин
T
1
/k
и
T
2
/k
для
дан
ного
давления
р.
Tal(,
для
i
р
=
т
k
допустимые
зиаче-
юш
растягивающих
сил
.
опре
деляются
любой
точкой,
ле
жащей
внутри
кривых
АВ
и
АС.
Легко
уб
Диться,
что
при
Д
йствии
только
раСТЯГИВaI
-
щих
сил,
пластичеСJ<ая
пло-
5
щадь
не
будет
окружать
о
т-
верстие,
если
давление
р н
е
будет
больше
k,
что,
очеви
д
но,
является
величиной,
при
"оторой
текучесть
возникает
по
J<раю
отверстия
при
отсутствии
растягивающих
сил.
Более
тог
о,
растяжение
должно
быть
мень
ше
той
велич:ины,
J<OTQ-
5г-
---
Т
;-----,---..,..--
,----::::
рал
определяется
из
\ , I
графи
ка.
Н
обходпмо
~
"
0
"
/
ч
7-
- 7
таиже
помнить,
что на
-
.
грузю!
должны
прила
-
;/;
I
~
га
ться
таиим
образом,
31----.
-~
-,--
/
ЧI
'
обы
ни
один
элемент
в
материале
не
оставался
ненагруженным
на
лю
боii
стадии.
Полны
е
1<0hшлеJ\свые
потенциа
ЛЫ,
по
которым
могут
быть
ВЫЧ:ИСЛ6ПЫ
напря
жения
в
упругой
об
ласт
и:
Т
/
К
l~
zL~~
~
---4
~~~
--+---~
254
ц
Q/a
Рll
,·
.
137.
а:
(~)
=
А
-г
k I n
(
с
+
~
;);
~
ш
= k 5
Г_
a
l
~~
•
2
c
~2
-
аl
(
ХП
.4 7
)
(Х
Н
А)

В
случае
всестороннего
растяжения
Т,
радиус
кругового
упруго
п
л
астичес
.
кого
контура
R
для
различных
величин
р
и
Т
может
быть
найдев
по
кривым
на
рис.
137.
95.
ПОЛНОСТЬЮ
ПЛАСТИЧЕСКОЕ
РАСПРЕДЕЛЕНИЕ
НАllPЯЖЕНИЙ
Рассмотрим
несколько
задач,
когда
весь
материал
уже
вступи
л
в
пластическое
состояви
,
и
когда
упругой
частью
полной
деформа
ции
мошно
пренебр
чь.
Здесь
будем
также
считать,
что
пластич
ес
кие
деформации
достаточно
малы, чтобы
можно
было
игнорировать
.квадраты
производных
перемещения,
так
что
обычные
диффер
n-
циальные
соотношения
(П.1)
и
(П.2)
сохрантот
силу.
Деформа
ция
должна
быть
в
условиях
плоского
напряженного
состояния
.
Условие
текучести
примет
форму
(ХП.7),
а
комбинации
напря
жений
8
и
Ф
могут
быть
выражены
через
функцию
напряж
е
ний
F
с
помощью
уравнений
(ХП.27).
Снеддон
*
предложил
при
ис
пользовании
метода
попыток
или
обратного
метода
решения
этих
уравнений
формулу
(ХII.49)
где
f (z, z) -
вещественная
функция,
которая
должн
а
быть
опре
д
елена
для
каждой
задачи.
Ясно,
что
такое
предложение
удов
л
ет
воряет
условие
текучести
и
с
помощью
(ХП.27)
может
быть
найде
на
со
ответствующая
форма
комбинации
Уравнения
Р
йсса
(Х.4З)
и
(Х.44)
тепер
ь
1
-....
.-....
-
dB
xx
= 3
(2хх
-
уу
-
zz)
dл;
1
.-....
...-..
-
аЕ
уу
= 3
(2уу
-
хх
-
zz)
dл;
аВ
и
=
О
;
d8
xII
=
;Уdл;
примут
вид:
)
I
(ХН.50)
.-..
j"-"
.-....
во
Tal{
как
zz
=
"2
(хх
+
уу),
эти
уравнения
сводятся
J{
следующим:
t - -
d€x
.<
= 2
(хх
-
уу)
dл;
1 - -
d8
1111
=
2"
(уу
-
хх)
dл;
d8
x
II
=
;УdЛ.
I
)
•
1.
S n
е
d d
оп,
Phil.,
Mag
., vol.
36
(1945),
р.
629.
(ХIl
.
51)
255

Когда
определим
вид
функции
t
(Z,
~,
станут
известными
велячипы
;;t -
уу
и
2;;;
!talt
вещественная
и
мнюrая
части
комбинации
Ф.
Далее,
уравнения
(ХII.51)
можно
проинтегрировать
и
получить
приращения
перемещения.
Для
этого
примеltf
dл
= Gdt,
где
t-
параметр
(например, вре
мя),
от
которого
зависит
развитие
Ш
l
асти
ческого
состояния
под
действием
нарастающих
наГРУЗОI<
и
G -
фУНКЦ1'lя
от
Х
и
у.
ПриращеlШЯ
ItОlt1Понентов
деформации
тогда
дu
ди
могут
быть
выражены
через
величины
дt
и
(ft,
Jюторые
обозна
-
ЧJШ
как
u.
и
v
и
будем
называть
скоростями,
везависнмо
от
того,
является
ли
t
временем
или
пет.
Уравнения
(ХII.51)
теперь
при
НИМaIОТ
вид:
a
l;
1
--.
---
- = -
(xx-уу)G'
дх
2 '
ди
1 -
--.
дii
=
t(yy-хх)G;
(ХН.
2)
дu
ди
-с
дii+~
=
2xy
.
И
СI<ЛЮ
ЧИВ
и
и
и,
получим
уравнение
дЛЯ
G.
О
днако
не
сиедует
из
этого
делать
правила,
таи
Kal,
иногда
лучше
наЙТlI
индивиду
альнъш
подход
к
решенmо.
А.
Сжатие
пластической
ПЩIТЫ,
заКЛIOчевиоii
между
двумя
параллельнымu
пластина
ш
Рассмотрим
плиту,
толщина
которой
2}~
веЛИfIИна
1алая
по
сравнению
с
другими
е
размерами.
Оси
координат
выбраны
так,
Рис.
138
как
ПОIШЗано па
рис.
138,
а
шероховатые
жесткие
пластIIвы
у
=
±
}~
перемещаlOТСЯ
друг к
друту
со
скоростями
~
= - v
при
у
=
h;
]
~
= v
при
у
= -
h.
(ХIJ.53)
в
этом
слуrlае
примем
n =
О
11
t (z, z)
тю(
что
t -
2п
(z -
z)
в
(ХII.49),
(ХII
.54)
Используя
(ХII.27)
и
интегрируя
для
определения
F (z, z)
можем
затем
получить
комбинацию
е,
которая
должна
быть
вещественной
6=:
[z+z
+
21tC
+{
4h2
+(Z-Z)ZI~
],
(ХII.55)
256

где
С
-
постоянная,
1\0ТОРую
можно
рассматривать
как
давление
8
точке
х
=
О,
у
=
lt.
От
д
ельно
взятые
компоненты
напряжения:
-
~'x
V
У
2
)
xx = k
-+
С
+
2
1-
-.
·
/~
h- ,
......
yk
ХУ
=
-т·
Уравнения
(ХН.52)
примут
вид:
дu
=
kG
l
,r
1-
у
'!
= _
д и
.
дх
У
h
2
ду
,
дu
+
ди
_
2yk
G
ту
ах-
--Г·
О
ТJ\
уда
,
интегрируя:
l'
V= - T
Y·
I
J
(ХН.56)
(./П
.
57)
Интересно
та({же
по
л
учить
траектории
1':
а
с
а т
е
л
ь
н
ы
х н
а
-
п
р
11
Ж
е
н л
Й,
т.
е.
лпнии,
к
({оторым
вектор
маКСИ1.1альног
о
}{асате.1ЬНОГО
напрящеuия
является
касательным
80
всех
ТОЧRах.
Их
можно
получить
из
Ф
ПОСI{ОЛЬКУ
(см.
8.
Главные
касательные
папряжеНllЯ)
наuравл
е
ЮIЯ
глаВllЫХ
напряжений
состаВЛЯ10Т
~
arg
Ф
1
и
п/2
+ 2" arg
Ф.
НапраВ.
ll
ения
максимальных
или
главных
каса-
телЬEIЫХ
напряженпи
пер
е
секают
главные
направления
под
углом
1
90
0
и
по::>тому
сос
т
авляют углы
±
п
/
4
+ "2
arg
с
осью
х.
Для
uаmей
задачи
из
(ХН.
5
4)
Ф
=
2:
[Vh
2
-
у2
-
iy].
По
э
тому
arg
Ф
=
аг
с
tg
-
у
/~
2
_
y
~
.
Дифф
е
р
нцпаJIьные
уравнения
nepBOl'O
се
fейства
тра
({торий
ка-
сатедьвых
напряжений
~~
= tg
(~
+ +
arg
Ф)
в
нашем
СJIучае
ау
V
h-
II u
dy
сводятся
!{
dx = }I +
~
,
а
для
второго
семоиства
- dx =
=-V'I
+Y
11-
у
•
17
д
.
Е.
Р
.
г
о;J.фР
К
25
7

Ин
те
грируя,
получим
решение
в
параметрическоЙ"
форме:
х
= h ( in
2е
± 20) +
А;
}
(ХП
.5
)
у
= h
со
20,
Р
ис.
139.
которое
представля
т
собой
два
сем
е
йства
циклоид,
по
J<азаввых
на
рис.
139.
Б.
Пластиче
кой
l
тlШ
Клин
из
пластич
ес
кого
ма-
терuала
:заключен
между
дву-
1Н
шероховатыми
ж
естк
ими
IJЛОСКОСТЯМИ
е
= ±
а,
которые
пере
ы
с
щаroтсл
д
ру
г
I<
д
ругу
С
угловой
СJ<ОРОСТЫО
(j).
Принимая
f (z, z) = 1
и
n = 1
в
(Х
II.
49)
ПОJ1УЧ\JМ
(ХН
.5
9)
Таl\ИМ
образом
ф'
=
Фе
-2iO
= 2ki.
("
П
.60)
р
Рис.
140.
Р
ис
.
1П.
Уравнение
равновесия
будет
уд
овлетворяться,
если
е
=
8'
= 2ki ln
....;.-
+
С
= -
4kO
+
С,
z
ч
то
приводит
J(
напряженному
СОстоянию:
-
........
1.)
тт
=
ее
= - 2k0 +
Т
С;
;е
= k.
(ХII
.
61)
I\омпо
но
нты
Скорос
ти
паiiдем,
выразив
(ХП.52)
в
полярной
форме:
t~
r
=
О;
ио
=
-T(j).
(ХII
.
62)
258

В
соответствии
с
рлс.
140
прпмем
С
=
О.
Тогда
на
стороны
клина
будет
д
йствовать
давление
р
= 2ka,
а
линиями
I\асательного
на
пряжения
будут
радиальные
ЛJ.тнии,
проходящие
через
вершину
клина,
и
окружности
с
цснтром
D
верШИR
клина.
Аналогично
можао
рассмотреть
От!ЮС
(рис.
141)
под
дейст
ви ем
давлепин
р
на
его
I
'
ОРИЗОRтальную
грань
О
х.
Принимая
С
=,
4k~
в
(ХII.61),
найдем;:;:
=
-2k
(~
+
О).
Отсюда
р
=
2k~.
96.
ОСТАТОЧНЫЕ
НАПРЯЖЕНИЯ
Таюю
напряжения
обнаруживаются
в
случае
то
лст
остенного
цилиндра,
плаСТИ'Ieская
деформацин
ноторого
описана
ранее
(см.
92.
Расширеnие
толстост
нного
цилиндра).
Будем
считать,
что
)\uвле
шrе
р
приложено
по
всему
Dнутревп
МУ
ЦИJlИвдричеСJ<ОМУ
контуру,
и под
го
действием
внутренняя
часть
ЦИ
J
lин
дра
стано
вптсн
п
лаСТ
П'1еСI<оii
,
а
внешнео
f<ОЛЬЦО
остается
упругим.
Это
при
во
д
нт
1<
Н
рав
енст
ву
р*
<
р
<
р**.
(ХН.63)
Сл дуя
полож
пиям
(см.
90.
ОстаТОЧllЫе
напряжения)
будем
счи
тать,
что
при
удал
нии
внутреннего
да
.
вл
нин
разгружени
имеет
упругий
xar>aI<T
р
и
оп
реле
яется
теми
же
упругими
постояннblМJf,
что
И
при
начальпом
упругом
llагружении.
Поэтому,
чтобы
найти
ОJ\ончате.rIьпое
папрюненнос
состояние,
пеобходимо
вычесть
упру
гое
решеЕНJ
С
,
при
"отором
С
внутрепuего
нонтура
r =
а
снимается
даВJlCпие.
Этим
р
ш
с
пи
е
м
будут
первы
два
уравлеElИЯ (ХII
.8)
.
Вычитая
их
лз
(ХII.16)
и
(ХII.17),
л
айлам,
что
остаточными
на
пряженuями
будут:
в
п
IaCTU'I
eCKo
u
области
а
-<
r
-<
'~
~
г
ра
2
(
Ь
2
)
rr = -
р
+ 2k ln
а
-
Ь2
_
а
2
1 - 7 ;
ее
'"
-
р
+
2k
(1 + 1 n + ) -
/~З
a~
(1
+
~
);
)
(ХIl.64)
в
упруг
о
й
оБJlасТIf
Н
-<
r <
Ь
I
(ХН
.65)
На
IJДСТЬ
теJlа,
расположеннуJO
.
в
обдасти
а
< r < R
будет
теперь
оказывать
давление
другая
часть,
расположенuая
во
внешней
Н*
259
