Годфри Д. Теория упругости и пластичности
Подождите немного. Документ загружается.


Эти
уравнения
найдут
применение
только
для
случая
сфериче
ской
симметрии.
Это
потребует
того,
чтобы
ив
=
и
ф
=
О,
u,.
=
и
(VII
.
7З)
и
все
величины
были
функциями
только
от
r.
ИЗ
уравнения
(УII.71)
тогда
найдем:
аu
u u
8
тr
=(jГ;
800=-;-;
8w=-r-
'
(VII.74)
du
2r,
u
Таи
что
расширение
составит
б
= -d + - ,
а
из
уравнении
зави-
r r
симости
между
напряжениями
и
деформациями
получим:
dr r
f"'dr
dr
r'
;:;:
=
л(~
+~)
+ 2 ..
аи
=
(1..
+
2/1)
~+
2л
~
'
)
00
=
<м>
=
л
(
~
+ 2
r
U)
+
2/1
+ =
л
~;
+ 2
(л
+
/1)
; ;
(VП.
75)
;е
=
eq,
=
;;р
=
о.
I
Из
(УII.
72)
найдем,
что
единственным
уравнение~r
равновесия
будет
i;:;
+
2;;--ОО-сР<Р
+ F
=0.
dr r
Р
r
(УII
.
76
)
Подставляя
напряжение
(УII.7
5
)
в
(УII.76),
получим
уравне-
ние
для
и
€f!и
2
du
2и
pF
r
=
О
dr
2
+-;-(jГ--;:г+
Л
+2
J.L
или
(УII
.
77)
Тан
иан
объемная
сила
F
r
является
фУПJ\цией
от
r,
то
это
уравпение
будет
вообще
интегрируемым.
А.
Сферичесиая
оболочка
под
действие!ll
воутренвего
п
внешнего
давлеmm
Рассмотрим
сферичесиую
оболочку
внешнего
Ь
и
внутреннего
а
радиусов
по д
действием
внешнего
Р2
и
внутреннего
Pl
давлеlШЙ
(см.
рис
.
54).
Так
({ан
объемная
сила
отсутствует,
инт
ег
рируя
урав
нение
(УII
.
77),
получим
в
и
=
А
•
+
-rг.
(У1l
.
78)
Из
(УII
.
75):
;:;:
=
(л
+
2/.1.)
(
А
-
~)
+
21..
(
А
+
~)
=
3КА
_
4~~
;
(УII.79)
00
=
ЗКА
+
2~:
.
(VП.80)
160

На
сферических
гравидвх
rr
= -
Рl
по
r =
а
и
rr
= -
Р
2
по
r =
Ь,
что
приводит
К
следующим
значениям
коэффициентов:
А
Рl
аЗ
-
Р21;З
В
=
(Рl
-
Р2)
аЗI;З
(УН.81)
=
зк
(I;З
-
аЗ);
4,...
(I;З
-
аЗ)
Тапгенциальные
напрnж
ния
на
l{онтурах:
(
00)
=
Рl
(2а
3
+
I;З)
-
ЗР2
Ь3
•
r=a
2
(113
-
аЗ)
,
(
00)
=
ЗРlа
З
-
Р
2
(а
3
+
2ЬВ)
r=b
2
(/)3
-
а
3
)
. ]
(УII.82)
Б.
Сферическая
упругая
оболочка,
окружающая
жесТI\УЮ
сферу
\
Жесткая
сфера
радиу
а
а
окруж
на
кон-
Рис.
89.
центри'Шой
й
оболочной
из
упругого
мате-
риала,
внешний
радиУС
ноторой:
Ь
(рис.
89).
Внешний
ноптур
060-
лоч
ии
подв
рж
Н
действию
нормального
давлепия
р.
Краевое
условие
для
этой
задачи
будет
смешанным.
Имеем
и
=
О
по
r =
а
11
;:;:
= -
р
по
r =
Ь.
в
Таиим
образом
из
(УII.78)
0 =
Аа
+
-2
И
из
(УII.79)
а
Откуда
4,...в
-р
=
3[(А
-
/;г
.
-
рЬВ
•
А
=
ЗКЬВ
+
4fJ.43
,
рЬВа
3
В
=
ЗКЬЗ
+
4,...а3
•
Тапгенциальuое
пап
ряжение
на
впепmем
контуре
получим
ив
(УII.80).
(УII.83)
63.
БИПОЛЯРНЫЕ
КООРДИНАТЫ
Это
е
ть
система
плоских
криволинейных
координат,
которую
можно
получить
из
конфор
шого
преобразования
1-
-1
Z+
ic
.,,
-
Н--
..
Z-LC
(V
II.84)
в
таном
случае
надо
полагать,
что
приемлемым
окаж
тся
метод
комплексных
потенциалов
(см.
54.
Применение
конформного
пре
образования).
Решения
такого
типа
для неноторых
задач
были
11
д.
Е.
Р
.
годфрп
161

даны
Стивенсоном
*.
Наряду
с
'
этим
Джеффери
**
использовал
общие
уравнения
равновесия
и
зnвисимости
м
жду
напряжением
и
дефор-
1ацией,
выражеввые
в
I<риволииейных
координатах,
для
решения
некоторых
практически
важных
задач.
Необходимо
привести
эти
у
х
результаты
к
виду,
ПОЭВОЛЯIOще
гi
применить
их
для
вычислеп'ИЙ.
Рассмотрим
сначала
гео
метрическую
сторону
конформного
преобра
зования
с
тем,
чтобы
получить
зависимость
между
пр
еобразовапuыми
и
натуральны
m
размераr.ш
физич
ских
тел.
Отделив
в
уравнеШlИ
(VII.84)
веществ
и
ную
часть
от
мнимой,
найдем
(рис.
90)
S =
1n
2
ТJ
=
АР
1
в.
Т
2
'
(УН
.
5)
Расстояния
r
1
и
r
z
опр Д
ЛЯIOтположени
точ
ки
P
1
относительно
дву
.
начальных
точеJ(
А
и
В
и
называются
б
и
п
о
л
я
р
н
ы
м
и
J{
о
-
В
о
р
Д
и
н
а
т а
м
и.
Ясно,
что
эта
систем
а
сим-
Рис.
90.
lетрична
относительно
оси
у.
1
ривые
~
=
=
сопstсоответствуютотношениIO
"/.,=
nst,П
поэтому
представлю
т
собой
окружности,
ц
втры
которых
лен
ат
па
'"
Оу,
а
I<ривые
ТJ
= const
или
AP1B = const
есть
окружности,
про-
ходящие
через
ТОЧJШ
А
и
В.
В
рассматриваемых
ниже
примерах
тела
будут
иметь
цилипдрическую
форr.Гi,
сечепие
которых
пред
ставл
я
ет
собой
две
окружности
S =
Sl
И
S =
S2'
На
рис.
91
показано
поперечное
се
чение
цилиндрической
трубы
с
эксцентрич
ным
цилиндрическим
отверсти
м
.
Известны
ми
размерами
обычно
являются
радиусы
R
1
и
R
2
И
расстояние
между
центрами.
В
ка
честве
величины,
определяющей
положеН1Jе
точки
на
контуре,
для
которого
!.озже
най
-
дем
тангенциальное
напряжение
ТJТJ,
примем
yrол
"(
от
оси
симметрии
и
установим
соот
ношение,
в
котором
он
находится
с
координа
той
ТJ,
также
опре
деляющей
полож
ние
точки
.
у,
Рис.
91.
Анализируя
уравнения
этих
окружностей
в
декартовых
коорди
ватах,
найдем,
что
координата
ТJl
илп
ТJ2
В
точке
Р
1
или
Р
2
выра
жаетс
я
через
"(1
нлп
"(2
уравнениями,
записанными
в
следующей
по
следовательности:
с
2
=
4~~
(R
2
-
d -
RJ
(R
2
-
d + R
1
)
(R
2
+ d - R
1
)
(R
2
+ d + R
1
);
(VП
.
86)
•
А.С
.
Stevenson,
Proc.Roy.Soc.,vol.184
.,p.129 .
••
а.
в.
J
е
r f
е
r
У,
Pril.
Тгап
,
Ноу.
Soc., "01. 22f,
р.
265.
16
2

t
с
sin
"\'1
g
111
= R
1
+ d
1
соз
1'1
(УII.87)
(УII.88)
Для
тоwи
Р
2
на
~
=
~
пую<ты
2
и
3
заменяIOТСЯ
выражениями:
(УII.89)
(УIl.90)
Рассмотрим
некоторые
задачи,
где
тангенциальное
напряжение
;.;]
задается
в
виде
функции
от
111
или
11
2'
ЦИЛlIllДр
С
эксцентричным
отверстием
под
действием
внутренне
го
давления:
.-....
P
1
R2 [ J
,,111
= -
Рl
+
2c
2
d2
(R~
~
R~)
(R; -
сР)2
-
R~
(R
1
+
2d
соэ
1)1)2
;
........
PIR~
[R2
R 2 2
(2
.32)2
]
""2=
2
(2
2)
2(
2-
dCOS1)2)
- R
1
-u
- .
2с
d2
R
1
+ R
z
Цилиндр
с
эксцеНТРIIЧПЫМ
отверстием
под
действием
внешнего
давления:
.-....
р
R2
1')1)1
= -
2C
2d2
(~;
~
R~
[(R: -
сР)2
-
R~(Rl
+ 2dcOSrJJ2];
~2
= -
pz
+
2c
2
d
z
~~~~
R;)
[R~
(R
z -
2d
cos
112)2
-
(R~
-
сР)2].
Полубесконечвая
плаСТlfН8
с
круглъrм
отверстием
под
действи
ем
давления.
Примем
~
=
О.
Тогда
из
(УII.85)
r
1
= r
z
,
т. е.
внеш
няя
окружность
превращается
в
ось
х.
Материал
пластины
теперь
занимает
все
полубескон
ечиое
пространство
у
>
О,
кроме
кругло
го
отверстия
радиуса
R
1
(=
R).
Рассмотрим
приведенный
выше
частный
случай,
когда
отверстие
подвергается
давлениIO
Pl (=
р),
например
при
заклепывании
отверстия
.
После
некоторы
'
преоб
разовапий
найдем,
что
в
точке
Pz
напряжепие
.-....
.z2-d2+R2
ХХ
= - 4pR
2
(.1:2
+
d2
_ R2)2 ,
4рШ
которое
принимает
максимальное
вна
чепие
d2
_ R2
В
Towe
О.
T
al{-
же.
вокруг
отверстия
Чтl
=
р
(1
+ 2tg
2
q»
С
максимальным
впаче
d2
+
R2
виом,
равным
Р
d2 _
Ri
н·
163

ПолубесRоuечnaя
пластшш
с
КРУГЛЫ
t
отверстие
I
под
деiiствие
I
растягивающих
СИЛ.
Предположим
(рис.
92),
что
пластина
нагру
жена
чистым
растяжением
Т,
параллльпым
ее
пря
fOлипеЙноr.:ry
краю,
а
отверсти
е
ЯВ
ляется
ненаПРЯ1f
еивым.
Эта
задача
также
рас
см
атривал
ась
Джефф
с
ри
,
а
позднее
была
мо
дифиц
ирована
Ми
ндл
и-
/(оэффuцuенmы1
конурнmм.цuu
нопряженщJ
о
mWKOX
о.х.
у
о
70ЧКОО
".о
Рис.
92.
Рис.
93.
ном
* ,
результаты
которого
мы
зд
сь
ПРИВОДИ?f('
На
рис.
93,
приведена
пол
убеСIЮН
чпая
пластина
с
КРУГЛЫt.l
отверсти
м под
дей
с
твием
растягив
ающих
сил
и
напряжения
в
точках
О,
Х
и
У
D
зависимости
от
величипы
d/R,
т.
е.
по
мере
того,
){ак
отверстие
прпближается
к
пряr.юлинеiiиому
I{раю
пластипы.
64.
ДР
l'ИЕ
РО
ДСТВЕНН
ЬШ
3
Д
ЧИ
Приведем
уже
получеuuые
р
ешеnия
пеI<ОТОРЫХ
задач
при
напря
женных
пластинах
с
I(руглы~m
отверстияr.ш.
Хоулеид
**
исследо
вал
с
л
учай
круглого
отверстия
в
пластипе
конечвой
ширины
под
действием
растягивающих
сил,
а
также
случай
большого
числа
отверстий
в
пластин
е
больших
разм
ров.
Лииг
***
исследовал
слу
чай
двух
!(руглых
отверстий.
ДаЛЬR
ЙШ
развитие
неlЮТОРЫХ
из
этих
задач отрю)
ено
в
работе
Савипа
****.
Ре
зультаты
этих
ори
гипальных
исследовапий
приведеиы
здесь
в
виде
графиков.
•
Н.
D.
М
i n d 1 i n,
Р.
.
Е.
8.
А.,
vol. 5.,
р.
56
(194.8)
.
••
R.
с.
з
.
11
о
w 1
а
n
d,
PhiL
.
TraL1
s. Roy.
ос.,
vol. 229,
р.
49.
R.C.1.
Howland
and
А.С.
8teven
оп,
ibid., vo). 232,
р.
155.
Н.
С.1.
Н
о
w 1
а
n
d,
Рсос.
Roy.
80с.,
vol. 148,
р.
471
.
•••
С.
В.
L i n g, J.
Арр.
Phy.,
vol. 19,
р.
77
.
••••
г.
Н.
С
а
в
и
п.
КОIЩеатрацня
паllРflщениii
nокруг
о т в
о
рстшi.
1.,
Гостехпздат,
1951.
164
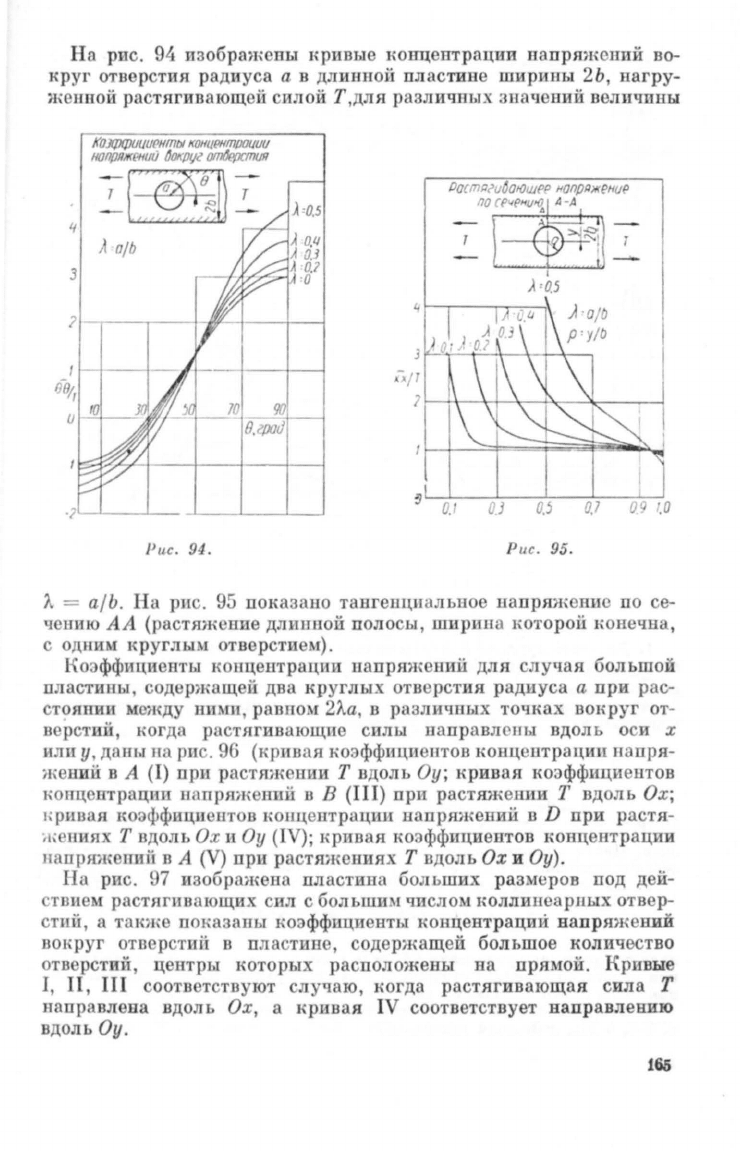
На
рис.
94
изобра>J,ены
Rривые
Rоnцеnтрации
напряж
ений
во
нруг
отверстия
радиуса
а
в
длинпой
пластине
ширипы
2Ь,
нагру
жеапой
рзстягивающей
илой
Т,для
различных
зпач
пий
величины
з
КОJффlJЦ/Jрнm/)/
/(oHIJpнmpOIJ/J/J
НОnPЯ
Ж
fJНlllj
60кptjг
IJf/1d(>pcm/JЯ
-~-
1
а Т
-о
-
"'
-
А
о/Ь
71
-.---,---
'1'--'---'---
-'--'----'-
--'
Рис.
94.
IJо
сmR?u
доюшр
р
нОПРRжеН/JР
-T-
@l
l-
1
"'
1
т
- ' -
,
; '
0.5
;,.
0/6
р
'
у /
6
Ри
с.
95.
л
=
а/Ь
.
На
рн
.
95
ПОI<азапо
тангепци
а
льное
папряж
вис
по
се
чению
АА
(растяж
ение
длишюй
полосы,
ширин
а
кото
рой
конечна,
с
одним
I{РУГЛЫ
1
отверсти
[).
Коэффициенты
:копцептрации
папрsш
евий
для
случая
большой
пластипы,
содержащей
два
круглых
отверстия
радиуса
а
при
рас
ст~
япии
между
ППМJ1,
равпом
2ла
,
в
раэлпqпых
тОЧRах
ВОН руг
от
верстий,
когда
растягивающпе
силы
направл
IJЫ
вдол
ь о
сп
Х
или
у,
дапы
па
рис
.
96
(крпвая
J\ОЭффИЦИ
нтов
ков.цептрацпи
папря
ж
епиi:i:
в
А
(I)
при
растяж
ении
Т
вдоль
Оу;
кривая
.
коэффици
е
нтов
!
<О
lIЦеIIТраЦIIИ
пanряжепий
в
В
(III)
при
растяжепии
Т
вдоль
О
х
;
Н
рllвая
l{оэффициептоn
конц
е
нтрации
напряжений
в
D
при
растя
;1\
пиях
Т
вдоль
О
х
и
Оу
(!
);
Rривая
I\о
эффициеп
тов
I{овцентрации
нanр
юкепиii:
в
А
(v)
при
растюкениях
Т
вдоль
Ох
и
Оу).
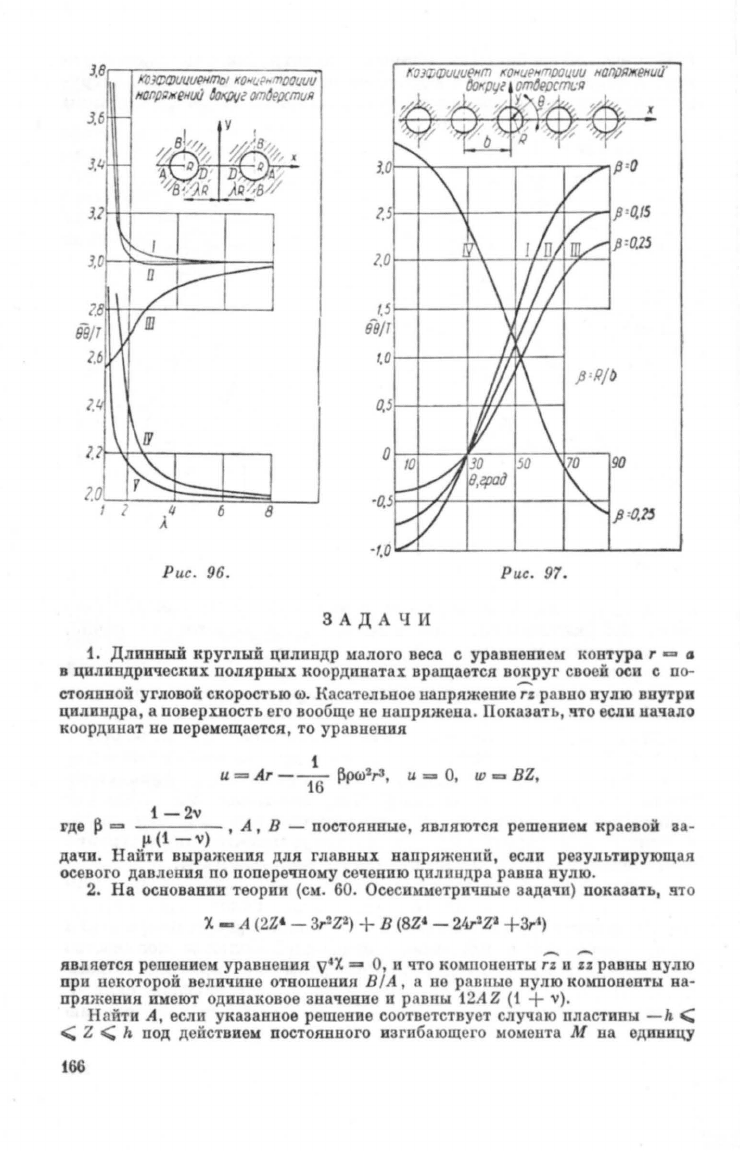
На
рис.
97
иэображ
на
пластип
а
больших
разм~ров
под
дей-
твпем
растягивающих
сил
с
болыпим
числом
коллиuеарпы
'
отвер
СТJШ,
а
таюне
покаэапы
I\оэффвциенты
концентрации
напряж
ен
ий
вокруг
отперстийв
пластине,
содержащей
большое
колич
ест
во
отв
рстий,
центры
которых
расположены
на
прямой.
Кривые
1,
П,
ПI
соотп
тствуют
сл
чаю,
ногда
растягивающая
сила
Т
направл
на
вдоль
Ох,
а
:кривая
IV
соответствует
направлению
вдоль
Оу.
165
3.8г--
r=1Ф-=-=-(J)U
-
(j
-
U
@li-m--О-
'
-КО-II
,-
'
".-m
-
t;О
-
I/U
--"
U
HO
npl1
Jr1MW
dotФt,;
г
(}(ТJ~elXmид
3.б
у
Ри
с.
96.
Рис.
97.
ЗАДАЧИ
1.
длlшный
круглый
циmшдр
малого
веса
с
уравнением
контура
r
...
4
В
цилвидричеСIШХ
полярв:ых
Rоордвиатах
вращается
ВОl(РУГ
своей
оси
с
по-
стоянвой
угловой
скоростью
00.
Касательное
напряжеш!е
7z
равпо
пулю
внутри
цилвидра.
а
поверхность
его
вообще
не
напряжена.
Показать.
:что
еслu
начало
координат
не
перемещается.
то
уравнения
i
-2"
~дe
~
=>
•
А.
В
-
постоянпые.
являются
решенnем
краевой
за-
J.L
(1
-v)
даЧJI.
HaiiTf!
выражения
дл
я
главных
напрпжепиЙ.
если
результирующая
ос
евого
даШIeНИЯ
по
поперечному
сечению
ЦИЛLllJдра
раппа
нулю.
2.
На
основании
теории
(см.
60.
Осесвмметричвъrе
задачи)
показать.
sтo
является
решением
уравнепия
V4X
=-
О.
н
что
компоненты;;
[1
;;
равпы
нулю
при
пеl(ОТОРОЙ
величине
отношения
В/А
.
а
не
равные
нулю
компоненты
на
пряжения
имеют
ОДПНaI(овое
значение
н
раппы
1
2
А
Z
(t
+
")'
Найти
А,
если
указа
.
llНое
решение
соотв
етст
вует
случаю
пластины
- h <
..;;;
z < h
под
действием
постоянного
изгибающ
его
моъrеuта
М
па
сдпющу
166

длиоы
обода
контура
r =
а.
П
окавать
Т
8RЖе,
что
есло
дОНТУР
средней
плос
КОСТИ
не
дефор
I1l
р
уется,
то
веремещения
средней
плоскости
будут:
U
r
=
О;
и%
=
3М
(1
-
'У)
(а
2
-
r
2
)/4Бhз,
rAe
Е
-
модуль
Юнга
п
v -
отношение
Пуассова
.
3.
НРИВ8Я
балка
пря
tОУГОЛЬНОГО
сечения
толщины
2h
пмеет
полук
р
углые
1t
11:
контуры
r =
о,
r
<=
ла,
(л
<
1)
в
промеЖУТRе
-2
< 6"""2
и
деформи-
1t
рует
с
л
струной,
соеДТПlяющей
,{Овцы
в
= ±
""2'
растягиваемой
сил
о
й
Т.
ПОК3З8ТЬ,
что
фушщил
оапршиений
Х
=
(Ат3
+ : +
С,
10
т)
соз
в.
удов
етворяет
кра
е
вое
условие
и
дает
нулевые
иапряженил
по
!
(
о
нтурам:
1t
r
=>
а
и
r
=-
1..0,
требу
~{ыe
реЗУЛЬТllрующuе
по
концам
в
= ±
""2
'
еСJJII
2В
С
Т
-
2Аа
2
=
л.
2
а'
- 1 +
л2
-=
2h
(1
+
л2)
lол
+ 1 _
л.
2
}
4.
Тяжелая
ТОНl(аll
баЛl(а
формы
клина
со
сторонами
в.,.
±
а
и
меет
точку
опоры,
расположеnвую
па
большом
раССТОIlПИИ
от
вершивы
.
П
о
казать,
что
но
м
поневты
наорлжеШ1Л,
ВОЗНnJ(ающ
1"0
в
результате
только
собственного
в ес
а
,
при
горазонтальпоii
оси
СIшметрип
будут:
- t
тт
=
Tpg
r {sio
в
(соsoc
2
а
+ 4) +
созес'
а
sin
зв}
;
- t
вв
=-
8
pgr
(З
in
в
(3 cosec
2
а
- 4) -
созес
2
а
sin
зв}
:
1
;:е
=
т
pgr
{соз
в
(4 -
созес
2
а)
+ cosec'
асоз
36}.
5.
Сферическая
оболочка
Ь
< r <
а
из
упругого
материала
заключена
в
жестиоо
сферичеСI(ое
ПOl(рытие
r =
а.
Внутренний
контур
оБОЛОЧRJI
r =
Ь
подвержен
ПОСТОЛlIВОИУ
давлению
р.
ПОf(азать,
что
глаВElые
нап
р
яжения
7r,
ее,
~
определлются
следующиъш
выражениями:
тт--
rAe
k -
упругая
постоянная,
выражеnие
которой
через
отношепие
Пуассона
имеет
ВИД
k = 1 + v
2(1-
2v)

r
лава
V/П.
СОСРЕДОТОЧЕННЫЕ
И
ПРЕРЫВИС
ТЫЕ
НАГРУЗКИ
65. П
Л
ОСJ
АЛ НАГРУЗКА
-
СОСРЕДОТОЧЕННАЯ
СИЛА
Р
ешения
уравн
ПИЙ
обобщенного
ПЛОСI{ОГО
напряженпого
состоя
ния
могут
быть
получены
таJ(ие,
!{оторые
хотя
и
удовлетво
ря
ют
необходииые
уравнения,
но
дают
б
сконечно
большие
значе
llИЯ
па
пряжеnий
или
перемещений
в
отдельпых
точках.
Анализ
сосредо
точенной
силы
и
момента,
полученный
из
таких
р
ешений,
хорошо
P~.
9 .
Рис.
99
.
согласу
тся
с
фотоупругими
испытапиями
*.
Праl\ТИЧ:
ки
можно
представить
себе,
что
эти
точки
с
особепuостями,
OI(PY)f
ены
вы
кружками
ИЛИ
полостями
в
мат
риал
.
Тю{
па
ри
.
98,
а
соср
едо
точенная сила
F
действует
в
точк
Р
J(OI1Typa
.
В
этом
сл
чае
по
не
большой
вы
кружке
в
материал
действует
ужо
некоторое
1<0
1l
Ч]JO~
напряжение,
IioTopoe
статиЧ'е
кл
ЭI<виваJI
птпо
СИЛ
Р,
а
согл
а
но
принципу
С
н-Венана
(см.
25.
Принцип
Сен-В
напа)
наПрЮI
еШlые
состояния,
возникающи
при
этих
двух
распр
делениях
паГРУЗ
Ю
J,
бу
дут
одинаJ<ОВЫМИ,
при
УСJIОВИИ,
что
paccMaTplIВaeM
точли,
ра
с
положенны
е
не
очень
БЛИЗJ{О
от
Р.
На
рпс.
9 ,
б
ПОJ{азапа
сила,
действующая
па
точку,
находящуюся
вuутри
материала.
Наряду
с
методом
введ
пия
татич
сJш
:>квивал
нтвой
Ш1ГРУЗКИ
по
угл
б
лению
можем
в
д
ополнепие
установить
у
JlОВНЯ,
Прll
J{
торых
обес
печива
ется
однозначная
величипа
пер
мещения
в
ТОЧI{е.
Прежде
всего
рассмотрим
случай,
когда
сила
приложена,
к
TO<IK
e
контура
упругого
материала,
и
дадим
реm
е
uие
по
lИ<Iеллу
,
110
в
выражении
через
компл
ксные
потенциалы
.
Расс
мотрим
компл
нсвые
потенциалы:
ер
(z)
=
А
]п
z;
'Ij
(z)
=
В
ln
z,
(VПI.1
)
•
М.
F r
о
с
h t, Plloto la Licity, vol. ii,
2,3.
168

где
А
и
В
-
постоянные,
которые
могут
быть
комплексными
вели
чина
ш.
На
основании
(VI.69)
без
учета
объемной
силы
...............
--
z - 1
ев
+ ir6 =
11"
(z)
+
11"
(z)
+
zq>"
(z)
+
--=-
'\>'
(z)
=
(А
+
В)
-=-. (VIII.2)
z z
Если
reперъ
принять
В=-А,
(VIII.3)
то
еДИНС'fвенnым
невулевым
компонентом
будет
;:;.,
которын
равен
~
(
А
::4)
тт
=
2
z+z'
(VIII.4)
Это
есть
радиальное
распределение
напряжений
Мичелла
*,
и
лег
но
убедиться,
что
с
уменьшением
r
напряжение
rr
стремится
J,
бескон
чности,
при
эт
ом
р
зультирующая
сила
по
полукруглому
углубле
нию
A1CB
1
радиуса
r
остается
постоянной.
Рассмотрим
ре
з
льтирующую
папряжения
в
точне,
в
которой
касательная
н
коп
ту
ру
образует
угол
а
с
осью
х
(рис.
99).
На
основании
(VI.38)
[
-
Z -
-
]В.
Х
+
iY
= - i
А
ln
z +
А-=-
+
В
ln z =
z
А,
[
z - Z
]те
;
(л-а)
= - i
А
ln
-=-
+
А
-=-=
2nA.
Z Z
те-
Ш
Необходимо
за
fетить,
что
эта
результирующая
не зависит
от
вели
чины
r,
которая
поэтому
может
быть
приията
I,aK
угодно
малой.
ПРИJIощенная
пагрузна,
статичеСRИ
энвивалентная
силе
F,
примет
тогда
значение
-
...
пА
п,
таким
образом
А
=
-~eil\,
2n
(VIII.5)
где
сила
F
направлена
под
углом
~
к оси
х.
Необходи
[ые
комп
лексные
потепдиаJIЫ
теперь
примут
ви
д:
q>
(z)
= -
;:
eil\
ln
z;
'\>
(z)
=
2~
e-il\
ln
z (VIII.6)
и,
поскольну
они
независимы
от
а,
направление
касательной
[,
контуру
пе
будет
иметь
значения,
при
условии,
что
ТОЧI,а
приложе
ПИЯ,
которую
прим:ем
за
начало
координат,
не
является
верш
иной
остро
го
угла.
• 1.
Н.
М
i
С
h
е
11. Proc.
LOlld.
{ath., Soc
.•
vol. 32,
р.
35.
169
