Годфри Д. Теория упругости и пластичности
Подождите немного. Документ загружается.


где
только
члены
с
положительными
степенями
cr
отличпы
от
нуля,
так
что
интеграл
принимает
зпаче.ви
:
1 - 1 -
6al~+
т
а
2
'
Ра
зл
ожим
(VI.136)
в
ряд
и
получим:
aO
+
al~
+
a2~:l
0'0
++~~
+
+а2
+
ьо
=
+те(2~++~З)о
ТaIШМ
образо
f,
прир
авнивая
КОЭффllllИ
BTы
с
ОДИНЮ<ОDЫМИ
степе-
1 - - t -
вя
ми
~,
найдем,
что
а
о
+ 3
а
2
+
Ь
о
=
О,
а
2
=
О,
а
1
+ G
a~
=
1 1
=
Т
Те, аз
=
12
Те.
Откуда
без
учета
постоянной
<i>оШ
=
Te(+~
+
1~
~:}
(VI.
t37
)
Далее,
(1
.127)
преобразуется
к
виду:
_ 1_ S
_1_.
1 -
6<14
<P~
(а)
d(]
=
2ni
За
2 +
а
4
•
а
_
~
+
'1'0
Ш
'1'
1 ( 1 ) s ( 2 1
аЗ)
(la
=--
-
-
Те
2а
-----+-
--=
2ni
4
а
ЗаЗ
3
O"
-~
'1'
=
-+те(2~
++
~З).
Интеграл
левой
части
может
быть
вычислеп
с
помощью
интеграла
Коши
при
условии,
что
полюс
пахо
ди
тся
в
лача
J
Jе
Rоордипат,
г
де
" R
~
(О")
а,
остаточnъш
член
составляет
о
= -
~
= -
(F"
и
ПРИliим
а т
~
"
1 1 -
~4
,
('")
а
1
т
перь
значение
Зf"
. 2 +
~4
<ро
':>
-
6г
'
тан
что
<i>
оШ
=
= -
+
Те
(
2~
+ +
~з)
-
i~
.
1-~4
2
+~4
Те(
+
+
_
~ _
~2
)
+
_
~
~
_
.
(
VI.1
38)
Окончательпо
комплексные
потенциа
'ы
упрощаются
к
виду:
<i>
Ш
=
Те
( +
~
+
4~
+ *
~з)
; J
(
1
91~
_
7~3
) (VI.13
9)
'1
Ш
= -
Те
~
+
84
(2
+
~4)
.
120
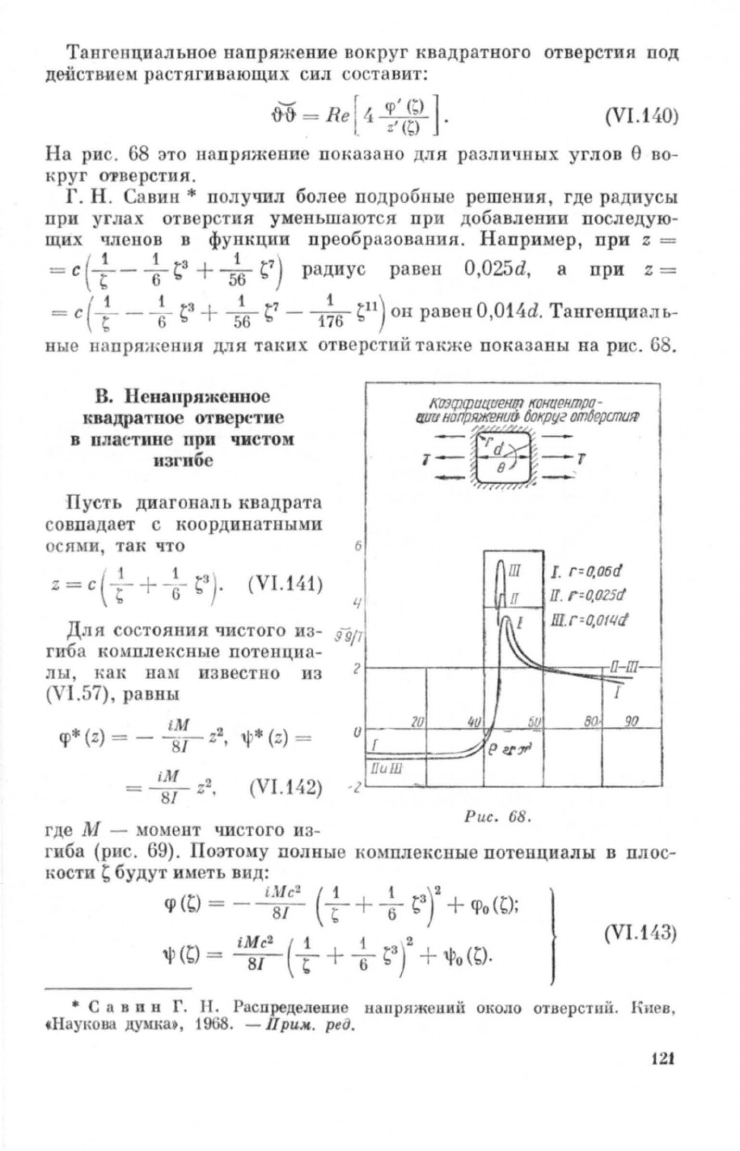
Тангелциальное
напряжение
вокруг
квадратного
отверстия
под
действием
ра
тягиваlОЩИХ
сил
со
тавит:
{t"5
=
Re
r 4
<1"
(~)
] (VI.140)
_
z
'Ю
.
На
рис
.
68
это
Ш:ШРЮI<еви
ПОI{аззно
для
различных
углов
е
во
круг
O'l'B
рстия.
Г.
Н.
а
виа
*
получил
более
по
дробные
решения,
где
радиусы
при
углах
отв
рстия
уменьшаются
при
доба
влении
последую
щих
членов
в
фУНКЦИИ
преобразования.
Например,
при
Z =
=
с
(_
1 _ +
~З
+
5~
~7)
радиус
равен
O,025d,
а
при
Z =
=
с
(+
-
-}
~3
+
;6
~7
-
1~6
~1l)
он
равен
O,014d
.
Тангевциа.;J
Ь-
ные
lIаПРЯil
еuня
д.ТIЯ
ТaIШХ
отверстиii
также
ПОI<азаны
на
рис.
68.
В
.
Н
I1аuрл
же
пно
е
квадр
а
тное
от в
е
р
ст
и
е
в
олаСТ
JПl
е
при
чи
ст
о
м
u
зг
и
бе
Пусть
диагональ
квадрата
овпадает
с
I<оординатпыми
осями,
так
что
(VI.141)
б
ч
Для
состояния
чистого
из-
99/
гиба
J\О!lшлеI<
ные
потепциа-
7
лы,
ка},
нам
известно
из
?
(V
I.57)
равны
*
( )
iM 2
и
tp
z = -
-
-
г
z ,
"'*
(Z) =
iM
2
=sr
Z
,
( 1.
142)
·z
где
lV!
-
момеllТ
чистого
из
{
ПиШ
ЮJэ~IJt:{l1ШUn
KOH(J!?FiIlIpO
-
f1{Д/'
НIJЛ
яжен'!Jl
Оокруг
omd
l?pCl
ГlI/R
-"
'Ь
.
'
-
Яl"~
·
-
1-
d "
-1
~
е)
~~-
~
~
1.
г
=о,обd
П
.
/":
O,0
25
d
rt
Щ,г
=
о,Оfllr/
о-ш-
[='
20
"и
j/)
80
90
А
ее?
Рш;.
68.
гиба
(рис.
69).
Поэто
JY
полные
}
ОZlшлеI<сные
потенциалы
в
плос-
J\ОСТИ
С
будут
им
ть
вид:
tp
Ш
= -
i~
~C2
(+-
+ +
~зУ
+
tpo(C);
_
iM
с
2
( 1 1
з)
2
'lJЮ
-
8г
Т
+
6"
~
+
"'o(~)·
\
(V
I.
14.3)
•
с
а
в
п
u
Г.
П.
Распределецие
uаLlряжеuиu
ОI<ОЛО
отв
е
рстни
.
Киев
,
«Науноna
дyмкa~,
1968. -
Прu;м.
.
ре
д.

Из
(V
I
.12З)
t;
+ i
~
=
i~;Z
[
~
а
2
+
3~~
- +
о"
-
3~
+
1 1
37
]
+
36
а6
+ 360'8 -
18
'
(VI
.144)
T
aI{
что,
используя
(VI.125)
и
интегралы
(2.17), (2.18)
приложе
ния
2,
найдем:
, '1 )
1 S
а
6 + 0'4
~~
(
а
'1'0
(С)
+
2лi
з
'
1 _
20'4'
а
_
~
da
=
'v
=
iM
c~
(~1'2
__
1
1'4
+
_1_
1'6
_
.2!-.-)
8!
3
'"
3
'"
36
'"
18'
Ри
с.
69.
Быqис
.
'IЯЯ
этот
интеграл
так
же,
I(аl(
в
предыдуще
{
прим
ре,
получим
без
учета
постоянпой,
которая
не
влияет
на
в
личину
напряжений,
(
1')
_
iMc
2
{~"2
_
~
1'~
+ _ L
_1'
O}
'1'0
'"
-
81
3
'"
3
'"
36
'"
.
( 1.1
4.5)
Далее,
из
(VI.127)
1 S 1 1 + 60'4
<p~
(а)
'Ро
Ш
- 2ni
за
2 -
04
а
_
~
da =
'v
__
iМс
З
{~1'2
_
-.!..,.4
+ _t_
1'6
_~
}
-
8!
3
'"
3
'"
36
'"
18'
а
подынтегральная
фушщия,
будучи
р
ГУЛЯРl10iI
вuутри
у,
I\poMe
начала
координат,
где
вычет
рав
н
пулю,
приводит
к
следующему
значению
интеграла:
1
-~.
Окопчательно
1
'Ро
(С)
-
зr
.
"
__
iMc
2
{~C2
_
~
r4
+ _1_
1'6
_~}
-
81
3 3
'"
36
'"
18
122
и
Dолю.tе
компленсные
потепциалы
после
преобрэ
з
ований
будут
им
ть
вид:
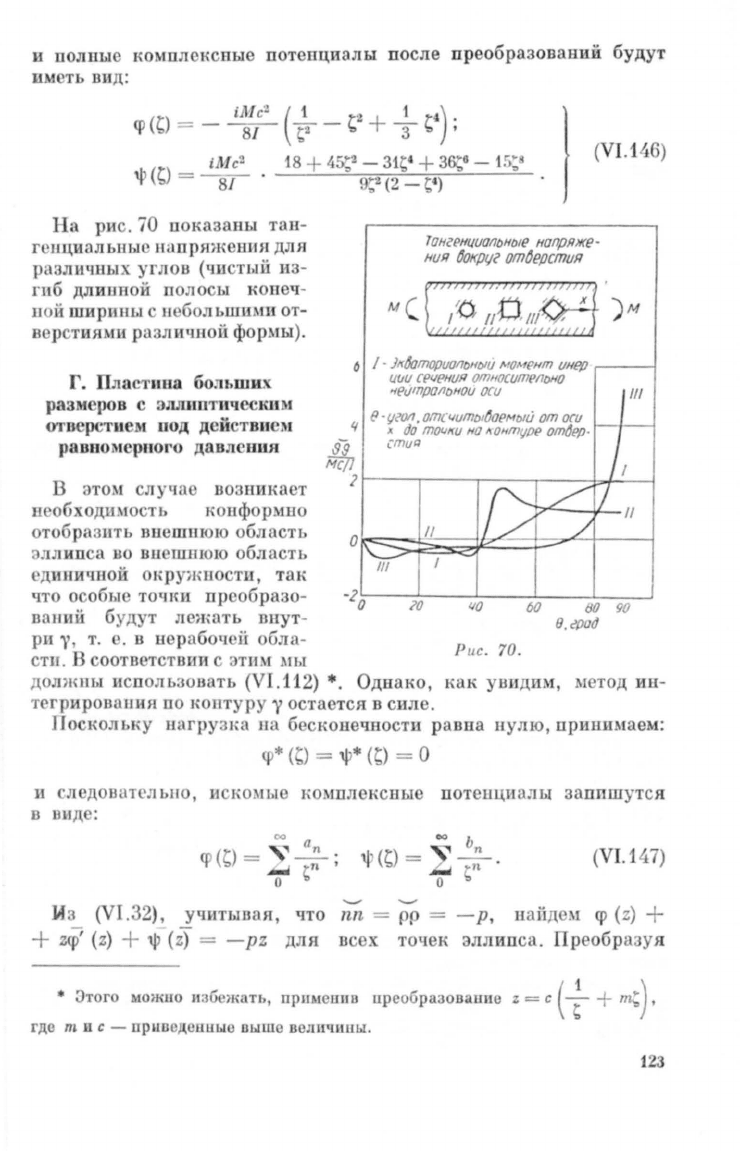
На
рис.
70
показаnы
таи
г
'
lщиальпыс
J1iшрящеаин
д,пн
различных
yr
J
IOB
('111
тын
из
ПI6
длиппой
поло
ы
копеч
п
о
й
ширп
ны
с
lI
е
БОЛЫШIАm
от
вер
тиями
различной
формы).
г.
П
л
аСТllEra
больши:
разм
ров
с
ЭЛЛ
lщттrч
есlm
1
отвер
ткем
под действием
равномерного
давл
IllIЯ
в
этом
случ
а
е
вознинает
п
оБХОДl1МОСТЬ
i\опфор~mо
отобра
з
ить
впешпюю
область
Э
ЛJшпса
во
ви
ШDЮЮ
об
{асть
е
диничной
I(РУЖПО
ти,
так
что
о
обыс
точrщ
прообразо
ваний
б
уду
т
JJ
жать
внут
ри
1'
,
т.
.
В
uерабоч
й
обл
а
сти.
В
оотв
тс
т
вии
С
ЭТIIМ
МЫ
. ]
(VI.146)
То
н
г@нциоnьны@
ноnряже
-
н
u
я
dOKPljf
оmdерсmuя
м
(
[:;:~~B~~§3
.
)
М
О
/"
j/(
оо
торuoл
о
Нt>lU
МОМрНт
U
Hf?/J
о
UIJU
C@iJ{,
HUP
от"оштелон
о
~@,jmРОЛО
Н
О{J
О(Ц
1
111
(J
"ljгол
.
отс
ч
uтОld
О{'
М
ОI/]
о
т
о(и
х
ио
точ
/(
u НО
_
онтljре
о
тОе
р
·
/
cmuQ
1
[2
L
7
11
11
/
'ii
I
10
БО
80
90
в
.срои
Р
ис
.
70.
Д
ОШIШЫ
использоuать
(VI.112)
*.
О
днако,
"ак
УВИДИМ,
м
е
тод
ИII
т
еГРИРОВЭIJИЯ
по
коптуру
l'
оста
тся
в
силе.
ПОСI<ОЛЬКУ
паГРУ
З
I\а
па
бесконе'lВОСТИ
равна
нулю,
ПрИНИ
l3ем:
* ( ) =
'р*
ш
=
о
и
сл
дов
ат
е
л
ЫIO,
искомые
I\омплексвые
потеuци
а
лы
запишутся
в
ви
д
:
(V
I.147)
И
з
( 1.32),
учитывая,
что
nn
=
рр
=
-
р,
ua
ii
Ae
M
ер
(z) +
+
z<?
(z)
+
'ф
(z)
=
-pz
для
всех
точек
эллипса.
Преобр
а
уя
•
:JTOГO
МОNШО
II
З
U
жать,
ПРШl
е
Пll8
пр
еоб
разоваuпе
z =
с
(+
+
m~)
,
г
де
т
11
с
-
npUB
CAeuuwe
оыше
пещrчиuы.
123

ЭТО
В
плос}(ость
~,
получим
для
всех
тО'!
}(
о}(руЖНОС
Т
II
у:
и
ли
<р(о)
+
(J~
2~:
0
2)
~'(-})+;Р(+)=-РСlО
+
';).
(V
I.14 )
1
d(J
Умножая
на
-2 . •
--t"
,где
~
теп
рь
внешняя
точка
по
отноше-
л,1
(J-
."
нию
К
у,
И
интегрируя
по
окружности
у
по
часовой
стр
Л1{
,паидем:
1 r
<р
(о)
do
1 r
(J
2 +
т
2ni J
(J
-
~
+ 2ni J
(J
(1
-
т(
2
)
v v
j
'
I 1
т
2п,
v
ф(+)d(J
=
-~s
_O
_+_."..:'_
do
о
-
~
2п,
0-
.
(VI.149)
v
При
ВЫ'шслеlШИ
первого
из
этих
внт
гралов
дою!>
пы
помнить,
что
у
т
перь
является
контуром
влеш
n
й
области
по
отнощ
енn
ro
к
еДИНИЧUОll
ОКРУ>IШОС
ТИ.
Необхо
д
имо
бу
д
l'
расс
мо
треть
JштеГР
И
РОl!I11ше
по
а
б
IЮНТУРУ,
состоящее
пз
Р
ис.
71.
окружпост
й
У
11
у'
боль
-
шого
ра
д
иуса
R,
соедин
Н
ных
посредством
лежащих
близко
дру
г
от
друга
отре
з
ков
АВ
и
CD
(рис
.
71).
Первый
инт
грал
,
согласно
т
ореме
Коши,
можем
IlЗОИ
сать
в виде:
<p(o)do + _ 1_ 5
cp(a)da
__
1_ r
о
-
Ь
2п,
а
- t" 2n, J
Б
А'"
у'
+
_1_
r
<р
(а)
da
= _
(~)
2ni J
а
-
Ь
IJ!
I
DC
<р
(о)
da +
o-~
так
как
весь
контур
заштрихованной
области
оБХ
Од
l1ТСЯ
в
отри
цательном
направлении.
Из
вида
фуmщии
<р
(о)
можем
заклIOЧИТЬ,
что
третий
интеграл
стремится
к
нулю
при
R
-+
00,
а
второй
и
четвертый
интегралы
б
удут
равны
друг
другу
по
величине, по
противоположны
по
знаку,
124

когда
точки
В
п
С
совпадают
с
осью
~.
Следовательно
1 S
<р(а)
da
= _
<р(1'").
2т
a-~
."
"
Подьшт
гралыrая
ФУШЩlJЯ
второго
ИDтеграла
в
(VI.149)
имеет
1
пот
сы
в
точках
О,
± - ,
~.
Ввиду
того,
что
только пачало
коор-
т
д
инат
ложит
вuутри
у,
этот
интеграл
берется
оБЫЧRЫ~f
путем
с
по
мощью
теоремы
выЧ'
тов
(см.
(2.14)
приложения
2).
Так
как
вы
чет
в
начал
КООРДlшат
составляет
(см.
(2.14)
ПРИJlожения
2)
lim
1(12
+
т
з
(р'
(_
'1_)
--
1
-,.-
=
О,
то
интеграл
равен
нулю.
о
....
/)
-
та
а а
-
..
Тр
тиii
иuт
е
грзл
из
(VI.149)
па
ОСDовании
теоремы
Коши
также
обр
а
ща
т я
11
н
у
ль,
так
(,ак
сдrшствеuвая:
особенпая
ТОЧI(а
подып
т
е
гральuоii
фУНКЦИИ
лежит
пве
у.
И,
наконец,
интеграл
в
правой
части
выражепия
( 1.149)
принимает
значение
- pcR
o
,
где
R
o
U
l'
аЗ
+
т т
е
тъ
вычет
п
нача
J
lе
координат,
раВElЫИ
1т
а-
"
= -
Т-.
о
....
()
."
'о
Складывая
результаты
иптегрирования,
полу'Тим
<р
(~)
= _
p~т
.
Беря
сопрященu
у
ю
фушщию
от
(VI.148)
и
снова
ИJlтегрируя
по
'{оптуру
у,
пойдем
_1 S
~
(+
)
da
21ti
а
-
~
v
+ _
1_
. S
а(\
+
mо
Э
)
2
ш
0 - -
т
v
ер'
(а)
da
+
a-~
1 S
ф
(а)
da
+
2
п!
о
-~
~
-
i~
S
(+п
+
:;)dП
v
Отнуда
б
3
учета
постоянной
~(1
+
~2)
~
2_т
или
v
<р'
ш
-
'P(~)
=
{С
'P(~)
=
_-.E.:...
-
рст
.
1
+
~2
(VI.150)
~
~ ~
~-т
Напряжения
теперь
IOгут
быть
получепы
из
(Vl.111)
и
в
час'l'
в
ости
[
'[
Р
=
I
=
Re
4 [
:"(~)
]р
=
!
=
Re
[4
02
~
m
].
Таним
образом
или
рр
+
00
=
......,...4.-,:-р_т
-;
(
co.--S
-::2
(}_-_т-;):-;;-
1 +
т
З
-
2т
cos 2{}
% =
р
1 +
2m
cos 2tt -
3т2
1 +
2m
cos
2t1-
+
тЗ
(VI.151)
1
25

Д.
Пластина
больпmх
размеров
С
ж
еС
ТJ\О
закреОJlекПЬ1М
00
коотуру
кругл.ы
~
(
от
верстиеlll
под
деiiствпсм
раСТЯГllваЮЩIl
..
х С
IШ
Обращаясь
к
рис.
56,
предположим,
что
отв
рсти
радиу
а
r =
а
фИJ\сируется
J\РУГЛЫМ
КОЛЬЦОМ,
к
!{оторому
матеРIIал
прил
-
гает без
зазоров.
По:)тому
краевые
условия
длл
вс
х е
зададим
в
виде:
ID]r
=a =
О.
Поскольку
объ
мные
силы
ОТСУТСТВУЮТ,
условие
,
налагаемое
на
КОАmлексны
потенциалы,
будет:
kЧJ
(z)
-
zcp
'
(z)
-
-ф
(z)
=
о
(V
I.
152)
па
r =
а
.
В
плоскости
~,
заданной
уравнением
(VI.12 ),
оно
оринима
т
вид:
Запи
ш
ем
kЧJ
(~)
- z
(~)
qJ'
(
~)
-1ji
(Q
=
О
.
;:.'
(~)
1
а
]
ЧJ
Ш
=
"4
т
Т
+
ЧJо
(~);
1
Т
а
'i
ш
=
-2
т+
'i'оШ
.
(VI.153)
(VI.151t)
Тогда
услов
и
е,
которому
у
д
овлетворяют
па
аа
= 1
Фуuкции
ЧJо
Ш
и
'Ро
(~),
запишетс я
сл
дующим
образом:
;:.
(а)
-.
(
1)
- ( 1 )
kЧJо
(а)
-
;,
(
-}-)
ЧJо
\ cr -
'Ро
cr =
= -
~
T(k-1)+-+Taa.
(
VI
.155)
1 da
Умиожив
на
2Лi'
а
_
~
и
проипт
ГРИРОВ
8 В
ид
ЛЬ
у,
найдем:
kЧJоШ
..L
- '1_. r
~~
.
(_1
)~
-ho
= _ _ 1
Ta~
I
2ш
J
аЗ
о
а а
-
~
2'
у
где
интеграл,
иак
мы
уже
видели
рав
п
пулю,
тан что
б
3
учета
постоявноii
ЧJо
Ш
= -
~:
~
.
Возъме
1
сопряженную
ф
ующшо
от
(VI.155)
и
ПОJlУЧИМ:
l«Po
(+)
+
аЗ
<р~
(<1)
-
'Р
о
(
<1
) = - +
т
(k
- 1)
аа
- +
т
: .
126

Откуда
опуская
постоя-нную,
~3<p'
(~)
-
'1'0
Ш
= -
~
Т
(k - 1)
a~
и,
следовD.телыl,'
о
q
ТёШИМ
образом,
полные IЮ~Ш
еI,сные
потенциалы
~IOГYT
быть
з
а
Dl1саllЫ в
ви
де
:
(VI.15G)
И
з
(VI.111)
по
л
учи
t
компопепты
напряжения
по
1\ОНТУРУ
отверстия
:
- 1
(2
)
РР
=
тТ
(k
+
1)
1 + k
СОЭ
21'}
;
~
= +
Т
(3
-
k)
(1 + +
СОЭ
21'}
) ;
':<\.
t
Т
k + t .
?А
pv
= 2
--
k
-·
10
_v·.
56.
функция
НАПРЯЖЕНИИ
ЭРН
]
j
(VI
.157)
Этот
метод
был
отн:рыт
р:шьш
,
чем
:
метод
компле1\СНО.й:
пере
мен
вод
,
Jt
п л
ская
задача
т
ор
ии
упругости
рассматрива
тс
я
в
11ем
сов
ршеппо
ины
[
с
по
собом,
применимым
1\
случаям
плоской
де
ф
ормаЦ
lfИ
и
обобщенного
плосного
напря-жепuого
состояния
.
TaH
oii
подход
все
еще
использу
тс
я
в
пекоторых
техн
ических
зада
ча
"
в
частности
в
тех,
ноторы
е
требуют
числеПRОГО
интегрирова
НИЯ,
а
также
как
ис
одный:
п уш{т
прн
примепении
интегральных
преобразо
в
аПИll
*
к
задаче
плоской
де
формации
.
Здесь
буд
м
польз
ова
ться дека
ртовы
!\
fИ
коордкиатами,
однак
о
в
гл.
ПI
даны
со
ответствующи
е
уравнения
в
полярных
коорди
натах.
А.
Плос(шя
деформация
В
том
'
слуtJае
перемещенпе
определяется
таким
образом,
что
w =
О
,
т
ог
да
на]{
u
и
v
неза
llИСИМЫ
от
Z.
Следовательно
на
основа
-
• D.
Е.
Н
.
G
о
d f r
е
У,
Qu. J.
ЫесЬ.
and
Арр
.
la
th
.,
vol. 8,
по.
2.
127

пии
зависимостей
между
дефо
рм
аЦИЯ~lИ
и
напряжения
1и
получ:им:
Т
ак
что
пли
дu
...--..
Е
дх
=
(1
+
",)хх
-
"'~;
дu
...--..
Е
-д-
=
(1
+
"')
уу
- v ;
у
;;='\119.
1
Уравнения
(II.35)
такж
е
преобр
азуютс
я
к
в
иду:
Е
(
::
+
::)
= 2
(1
+
"')
?у;
)
yz
=
xz
=
О.
У
равне
ние
равно
веси
я
принима
ет
форму:
()
...--..
8?у
J
дХ'
(хх
-
рУ)
+
ау
=0;
д?У
8...--..
-8-х-
+
~Oy-
(уу
-
рУ)
=
О,
г
де
,
!<ак
и
раньше,
F =
-gr'ad
У
.
(VI.15 )
(V
I.159)
(V
I.
160)
(VI.16t)
i7т
и
д
ва
уравнения
могут
быть
одновреи
ино
удо
в
летворены
с
помощью
функции
Х
(х,
у),
где
.........
(J2X
V
хх
=--
+
р
;
д
у
2
.........
8
2
Х
УУ
=
дх
2
+
рУ;
д
2
Х
ху
=
---
8хду
.
Х
называется
Ф
у
и
н
Ц
и
е
й
Э
р
и.
(VI.
1
62)
д
2
д
З
Используя
оп
е
р
атор
\72
=
дх
2
+
8
п
2
'
и
сл
ожив
п
ер
вы
е
два
урав-
нения
(УI
.162),
найдем
19
=
2х
+
2pV.
(VI
.
163)
128

Таним
образом,
У<rнтывая
( 1.15
9)
= (1 +
v)(V
2
X + 2pV).
(VI.164)
Теперь
можно
Dыразить
деформа
ции
в
(VI.158)
через
ф
у
нкцию
нап
ряж
ений
и
зате
м
JI
КЛIOЧИТI
,
и и
v
из
ЭТИХ
урав
нени
й
с
помощью
ураопе
llиii
(VI .160).
-
то
привадит
R
Фун
да
.
\lентально
'lY
уравпепи1О,
I{ОТОРОМУ
ДОШJ;ца
довлетвор
ять
фушщия
напряжений:
v4
1
1..
+ 1 - 2"
W}
=
о
"
1-"
Р
1 .
(VI.165)
Для
удобства
ззпн
ш
м
ГО
в
ви
е
V = 2W
1
.
(VI.166)
ПОЛОЖИВ
х
-.,..L
1 -
2,
' W
1 -
л
I '1 _ v
Р
l '
(V
I.167)
ПОЛУЧИМ
(VI.
16
8)
Теперь,
очевидно,
все
КОМDОиепты
де
фор
мац
ии
и
папрящения
могут
быть
выр
ан
пы
через
ф
ушщи
1О
1..1
'
](Qторая.
удовлетворяет
б
и
г
а
р
м
о
R
И
Ч
к
о
м
у
у
р
а в
в
е
в
и
10
(VI.168).
В
раз
верпуто!
i
де
l
артовой
фОР~IС
;}ТО
уравнение
име
ет
вид
д
~
X
д
4
Х
д
~X
l + 2 1 +
1-0
дх
4
д
х
2
д
у
2
---ауг
- .
(V
I.169)
Его
решепие
прим
еl1ительuо
к
пекоторым
плоским
задачам
значи
тельно
сл
ожн
ее
уравн
ния
Лапласа
.
Кроме
того,
I<рзевое
условие,
требуroще
,
чтобы
была
задана
пекоторая
комбинация
I
омпонентов
на
пряж
пий,
таЮJ\е
тр
бует,
чтобы
была
задана
вторая
производ
ная
от
х
1
•
И
,
наков
Ц,
как
увид
им
далее,
ко
мпо
ненты
п
р
еме
щения
не
могут
быть
выраж
ен
ы
только
через
функцию
1..1;
дл я
их
выраже
ния
дополпитель
по
потр
буетс
я
еще
Фуmщия
перем
е
щ
еllИ
n
"'1'
Все
эти
трудности
сдерживал
и
прогресс
в
ра
з
витии
ПЛО
С
I<ОЙ
задачи,
и:
только
при
1 иеаи
RОМПЛ
I<
С
НЫХ
потенциалов
позво
л и
л
о
сущ
,
т
B8
liDO
продвипуться
вперед
.
Б.
ОбобщеНllо
е
1
1ЛО
кое
н
апряженно
е
С
О
С
ТОЯ
ПИ
Это
со ТОIlПИ
опр
едел
я
тся
условияr.ш
(VI.42).
Применяя
мето
д
усред
пения
по
толщии
2h
пластины
(см.
51.
Обобщенное
ПЛОСI<ое
па
llрmКО
НRо
е
состояние),
получим
уравнения
равновеt:ИЯ
(1
.21)
в
СJJедующем
виде:
д
~
д'ХУ
о
-
(хх
-
РУ)
+ - = .
ох
ду
'
аху
d -
О
ах
+
ау
(уу
-
PV)
= .
1)
д
.
R.
р.
ГОnФРI.
{.
