Годфри Д. Теория упругости и пластичности
Подождите немного. Документ загружается.


54.
ПРИМЕВЕНИЕ
r
ОНФОР~Ш
го
ПРЕОБ
Р
30ВАПИЯ
Общие
свойства
коuформного
оответствuя
tеж
ду
точкаj\ПУ
в
плоскости
z
п
плоскости
~
даиы
в
ПРИЛО
/I,еп
ии
2.
Вв
дем
обозначе
ния
для
КОfoшонентов
напряжеuиii
и
других
велllЧIПl
q
рез
I{o~r
плексные
потенциалы.
П
усть
Z = Z
(~)
= f
(;,
,,)
+ ig
(~,
,,) 1.
96
)
есть J{ОВфОР~1Ное
преобравование,
где
~
= ; + i", t
(;,
,,)
и
g
(;,
11)
-
в
ще
твенная
и
м:иимая
части
функции
Z
(~)
.
На
рис.
63
показаны типичные
кривые
; =
con
t
и
11
=
со
t.
Каса
тельная
к
кривой"
=
const
образует
угол
а
с
осью
х.
Веl
торы
напряжений,
действующие
по
элемептам
этих
кривых
в
точк
Р
,
югут
быть
разложены
на
составляющие
по
направлениям
~
и
".
Таким
образом
по
элементу
кривой
~
=
CODst
нормально
uапряжение
будет
Ц,
а
касательное
~,
тогда
ка1\
Д
R
3.'1
{епта
иривой"
=
соn
.
L
имеем
соответственно
.;r;
и
(тi.
По
тому
1,0
fбива
ции
напряжений
:\10ГУТ
быть
представл
ны
в
виде:
8'
=
~
+
Чri;
ф'
=
~
-
~
+ 2ir,;
)
( 1.97)
и
вязаны
с
иомбинациями
в
деиартовых
осях
по
10ЩЫ
завя
п-
мостей
8'
=
(
УI
.
9
)
Выразим
теперь
величину
e
2ia
в
соотв
Т
твии
пр
обраЗОВ:lllllе\f
(VI.96).
Приравнпвая
вещественную и
)шшrу1О
части
этого
урпв-
пения,
пол
чим:
х
=
f(~,
,,),
у
=
g(;,
11)·
(
1.
9)
Наклон
кривой
т]
=
соп
t
составит:
(
ау
) (
*~
) (
:f
)
Lg
а
=
dз:
11~СОПЗ!
=
.!.L
a~
=
д!
(V
I.1
О)
~
l1
= COlIst
д~
l1
= const
Возы!
М
ча
тву1О
производную
от
(VI.96)
по
;
,
(1')
1 = .!.L + .
~
Z",
д~
l~.
Ti1IHIМ
обр~зо
r arg
z'
(~)
=
ar
Т
перь
мощем
написать
11
0
дк
дГ
tg
aг
=
а.
дГ
(
1.1
t)
(VI.102)

где
1
U
=lz'ШI=
!
Z
/
(~)Z/(
~)
}2
(VI.10
3)
и
-2«
z'
ю
е
=
:.'ю
(VI.104)
СJI.
чае
отсут
твия
оБЪ('\lНI>1Х
с
ил
1Ы
видели,
что
('-)
- 2
(
ер'
(z)
+
ср'
(z)
);
ф
= - 2
(z
Q'
(z)
+
1F
'
(Z)),
}
(V
I.105)
г е
~2'
(z)
=
<р'
(z).
(У
l
.
106
)
3а~е1IЯН
;;
па
z
Ш
в
( 1.9 )
и
нсп
.'
tьзуя
(V
I.10
1)
,
полу
ч
им
(-1'
= 2
'~
t-
<р"'
(б
}.
t
z'
(
~
)
?
;;-
,
? - -
--
<1>'
- - ;'"( ) { z
Ш
~~'
Ш
+
'Ф'
(
)},
)
1.107)
где
]
~oгдa
мы
ВЫРВiI
В
М
:ко,\mле"сный
пот
пци3.л,
например
.
ер
(z)
,
чер
;}
ФУJПщия
ер
!
:;
Ш
J
д
о
лжна
быть
записава
м
а
к
ер
Ш,
н
-
мотря
на
т
о,
что
деЙст
ви.т
львая
фУНКЦИЯ
будет
иметь
д
р
угое
з
н
а
ч
пи
.
П
О:ЭТО
МУ
<р
(~)
означает
мо~шл
ксный
Dо'Ге
nциал
<р
(z),
В3
Шl
са
нв
ый
n
ви
д
фУНКЦИИ
от
.
Все
:КОJ1фОР"tВые
пр
е
обра
з
овапия,
приве
денп
wе
в
:этой
r
а
в
,
отобраrкают
задавный
иовту
р
в
п л
оскости
z
в
единичную
о
кру
п
..
-
во
ть
В
п
лоскости
~.
ПО
тому
здесь
будем
ч
а
ще
по
л
ьзоваться
по
лярн
ыми
но
р
Д
пн
ата
ми
(р,
")
в
П
ЛОС
I{ОСТИ
~
(рис.
63
а
).
ледо
в
а
тельно
1.10 )
Рассматривая
э
лементы
в
ТО
Чliе
Q
(см.
рис
.
63,
а)
по
кривым
р
=
= const
,,
=
оп
t,
получим
новые
компоненты
напряж
ния и
со
ответств
вво
запише
м
"
=
pp
+
~.
фn
=
pp
_~+
2
i~,
]
(Vl
.
109)
где
е
"
= '
ф
.
=
ф'е
-
2
i
~
=
~
.
ф'.
(
Уl
.
11
0
)
111

В
выражении
через
I,О?rшле!(спые
потенциал
ы
8" = 2 J
ер'
ю
I
q;'
(
~
)
}.
l
z'Ю
т
z
'Ю
'
~
2~
- , - - , -
ф
= -
~z'
Ю
{
zш
Q
Ш
+
'"
(~
)}
.
]
(Vl.111)
Эти
фор
{улы
будут
использованы
для
нахождения
коль
цевых
на
пряшеuий
по
контуру
отверстия
в
плоскости
z,
прсобразоваrrного
а
у
(
'
СОМ!
Г
~st
~
l-nлоскосmь
б
Р
ис.
63.
/
l
'
f/fI(юФrmо
t;
'
плоско
сm
Р
ис
.
64.
в
единичную
о
кр
ужность
р
= 1
в
ПЛОСl\ОСТИ
~.
Прив
ед
Af
при
1ер
применения
этих
уравнений
и
способа
ПОПЫТОК
в
ПЛОСIЮСТIf
~.
Эл
mш
ти
ч
ес
ко
е
отверстие
в
пла
с
ти н
е
Б
О
ЛЬШIJХ
раз
lе
ро
в,
находя
щ
ейся
под
д
ейст
в
ием
р
аСТ
Я
l'
Я
.
ВaIОЩ
ИХ
С
ШI.
Согласно
соотношению
(VI.112)
внешняя
обл
а
ст
ь
эллипса
с
ПО.'Jуосями
а
и
Ь
в
ПЛОСI(ОСТИ
Z
пр
бр
а
зуетсн
во
внешнюю
область
едипичвой
ОI{РУЖНОСТП
у
В
ПЛО
СI
ости
~
(рис.
64),
где
1
а-Ь
с
=
т(а
+
Ь),
т
=
1l+lJ
'
(VI.113)
Вместе
с
Ter.t
х
=
а
соз
t},
у
=
ь
sin
t},
так
что
t}
есть
угол,
с
остав
ленный
радиусом-вектором
с
большой
полуосью
ЭЛJfIlпса.
ТОЧl{И,
в
которых
преобразование
перестает
быть
1,ОНфОРМНЫМ
,
определяются
уравнением
z'
(~)
=
О,
т.
е.
опи
располагаются
па
окружностях
~
= ± v
m
~
посI<олы<y
эти
окружuо
ти
ежат
внутри
еДИВИIJЛОЙ
окруншостп
и,
следоватеJIЫiO,
не
на
материальпой
части
плоскости
~,
то
полученные
результаты
будут
приемлемьвm.
В
противном
случае
получим
точrш
:,
В
I(ОТОРЫХ
напря>кеиия
будут
бесконечно
большими.
Краевое
условие
по
ненапряжеI1RОЬ1:У
контур
элшшса
имеет
в
и
д:
(j)
(z)
+
zcp'
(z)
+
'i>
(z)
=
О,
а в
выражении
через
~
(j)
(~)
z,
а}
+ z
(~)
ср
'
(~)
+ f(Q
i!
(ц)
=
О
,
112
- - 1
гдо
т .rюръ
можем
положить
~
=
<1.
~
=
<1
=
а
па
у.
так
что
q>
(о)
z'
(
~)
+ z
(o)~'
(-})
+
'ii
(-} )
z'
(-} ) =
О.
(V
I.114)
Б
з
учета отверстия,
ко~mлеRспые
потенциалы
в
плоскости
z
на
ОСlJоваюш
1.54)
будут
задапы
следующими
фующ
иями:
. 1
Т
* ( ) 1
Т
-2i(%
<р*
(z)
=
т
z;
'ф
z = - 2
е
z.
Преобразуя
D
ПЛО
Сl\ОСТЬ
~
И
принимая
больmие
зпач
ния
величины
I
~
I
для
получев:ия
условии
па
б
еСl{ОП
чпости:,
получим
<р*Ю
=
+
Tc~;
к
этим
величипам
ДОШ
ЮIЫ
стремиться
полпые
комплекс
ные
потенциалы
<р
(
~)
11
'ф
(~)
при
(~)
_
00
для
того,
чтобы
дать
ИСr<омые
растягивающие
силы
[Ja
бескопечпости.
Для
достижеrrпн
условия
пепа
пряжеппого
ЭЛЛИDти([еСI\оГО
отверстин
эти
УСЛОВИЯ
ДОЛ>I<
Rы
быть
дополпеаы
доба
вочвыми
члепами.
Так
иак
усл
ови
па
б
скоп
чиостn
остается
пеизм НПЫМ,
в
~ТИ
чл
пы
будут
входить
толы
о
отрицательные
степени
~.
Коэффициент
концентоа
ЦlJи
напряжениu
dокруг
OmtJe
pcтU
R
~~
~
~.S~S
8
-
зксц
е
нтРIJ
l/ныiJ
s-
угоп
_
,.._
~~~~~~~~~~~
/
1l
/~:X,
'\
\
I/
/ ,
З~~~~L-~~~~~
~
Л
~
I I I
89!!
I
Ш
I 1 /
~u2
~+7~----r---~~~~
'1/
9Q/S
I
f/
'.,
'1
/
k/
I
qO
6lJ
80
90
S
-
граи
16/0=2/3;
ЛЬ/а
=
f;
ШЬ/tr=З/2
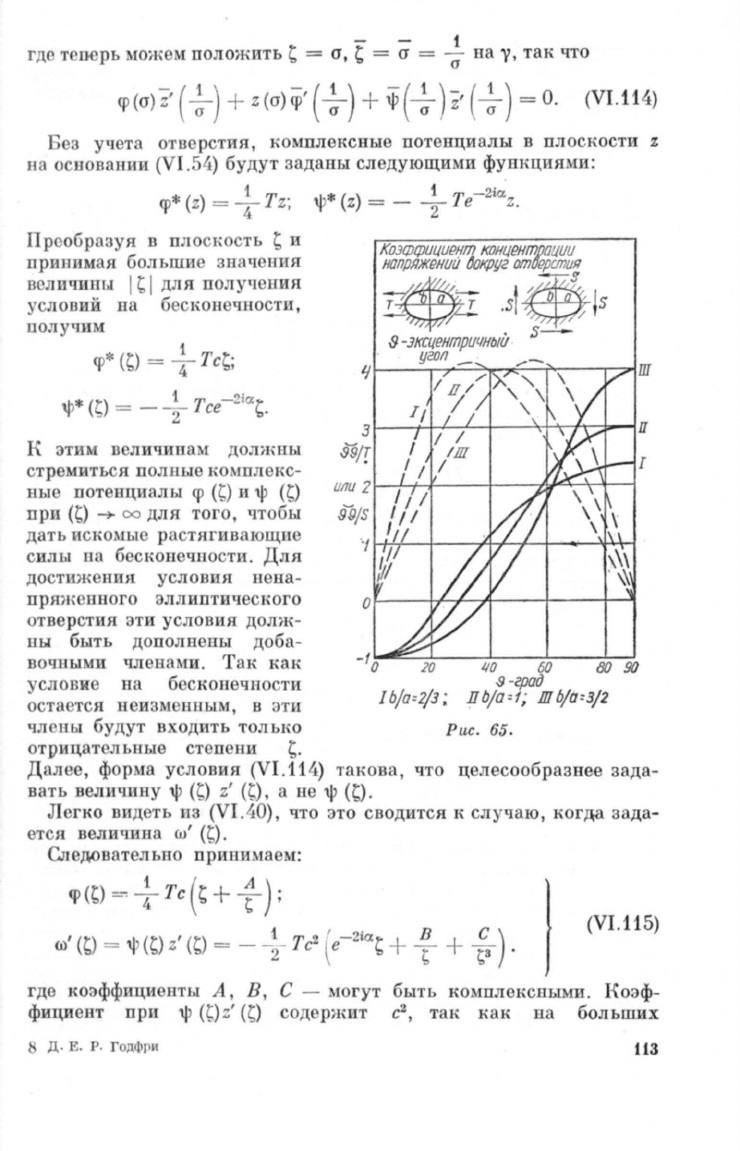
Рис.
65.
Далее,
форма
условия
(VI.114)
таиова,
что
це
лесообразп
ее
зада
вать
величину
'Ф
(
~
)
z'
(
~
),
а
пе
,~
(~)
.
Легко
видеть
из
(VI
.4
0),
что
это
сводится
I{
случаю,
когда
зада
ется
величШtа
(1)'
(~).
Следовательпо
припимаем:
<p(~)
=+
Tc
(
~
+
~);
ro'
(О
=
ЧJ(~)
z'
(~)
= -
~
Тс
2
(
e-2Цx~
+
~
+
~).
J
(VI.115)
где
J\ОЭффИДИ
пты
А,
В,
С
-
могут
быть
J:(оъmлекспыми.
Ко
э
ф
фициепт
при
'Ф
(
~
)
z
'
Ю
содержит
с
2
,
так
как
па
больших
Д
.
Е.
Р
.
Г
ОДФР
II
11З

раССТОЯDИЯХ
z'
(~)
~
с.
При
подстаНОВJ(е
1.11)
в
(VI.114)
буд
~!
иметь
члены
с
треаlЯ
раЗЛИЧНЫМЕ"
тепенямп
(1,
и
СJ\И
ИХ
JtОЭф
фици
енты
приравнять
пулю,
то
иэ
р
шепия
по
л
уч
штых
уравнсниu
найде
r:
A=2i
i
r:J._
m
;
С
2ir:J.
=-е
.
в
= 1 -
2т.
о
2а
+ m
2
; }
(Vl.116)
Тапгепциальные
напряжепия
по
копт
ру
эллипса
могут
быть
получены
из
выражения
t1д-
= [8"
]
Р=
l
= 4
веществеuuая
часть
[
ер'
(~)
1
от
~
Р
=
l'
или
~
1-т
2
-2со
2«(%-~)
+
2mc
o
2(%
----т-
= 1 -
2т
cos
2& +
т
2
(VI.117)
Эта
величина
представляет
собой
I<оэффицпепт
копц
птрации
на
пряжений
по
контуру
ЭЛЛИDТIIЧ
CJ{OfO
отверстия.
Представляют
иптерес
следующие
частные
слу']ап:
а
=
О,
по
этому
~
1
+
2m-m
2
-2со
2&
'i'
= 1 -
2m
со
э
2\} +
щ
2
Н
а
ри
.
65
(эллиптичеСI<ое
отверстие
в
пластип
больших
р
3-
М
ров,
находящейся
под Д
йстиием
растяжения
илп
с
д
вига)
:.ITa
величина
дана
для
различных
значен:ий
bJa
в
ТОЧIШХ
гд
угол
меж
ду
радиусом-вектором п
большой
осью
ЭЛЛИDса
равен
t).
Примем
а
=
45
0
и
Т
= - S;
а
= -
45
0
J[
Т
= S.
Сl\лаДblвая
эти
решения,
получим
чистый
дииг,
D:lралл
льuый
Ы.
4
sin
2\}
осям
:щлипса,
для
1<ОТОрОГО
-s
=
1-2тсо
2~
+
т
~
(КРИВЫС,
со-
ответствующие
этому
случаю,
DОJtазаны
на
рпс
.
65
пупнтиром)
.
55.
ПРЯМОЙ
МЕТОД
МУСХЕЛИШВИЛИ
Из
приведеииого
выше
примера
видно,
что
метод
ПОПЫТОI{
при
водит
I<
положительным
результатам,
если
удается
сд
лать
60
[[0
-
nанвое
предположение
относит
льно
формы
JtОМDлеI<
пых
Dотеп
циаJ\ОВ
<Р
Ш,
'"
Ш,
которые
в
этом
прииср
были
заданы
выр
же
lIИЯМИ
(VI.116).
Н.
и
.
Мусхелишвили
разработал
метод,
в
НОТОрОМ
с
помощью
1<омпле]{сного
иптегрироnаиия
JtОМПJ\еl,СНЫ
потет~иалы
могут
быть
получены
непосредственно
в
виде
рядов.
Этот
метод
при
меним
к
пеСКОJ\Ы(ИМ
зада'Iам,
n
ноторых
рассматрпвают л
пласти
ны
больших
размеров,
ослабленные
отверстиями
различной
формы.
114

Эти
задачи
выбрапы
Та1(ИМ
образом,
чтобы
проиллюстрировать
краевые
условия
,
ВОЗUИI<aIощие
в
сл
ед
ующих
случаях:
наГРУЗl(а
прилож
на
на
бол
ьшом
расстоянии
от
отв
ерстия
и
отверстn
вобо
д по
от
папряжепиii;
нагру
з
к
а
распр
еделе
на
по
КОНТУРУ
отверстия
и
пластина
н
е
lI
а
ПРЮJ
о
а
на
б
КОJl
О
ЧЯОСТИ;
задапы
пер
м
щения
по
новтуру
отверстия.
Необходимо,
чтобы
отверсти
е
L
могло
быть
IЮПформно
преобра
зо
вапо
в
единичную
окружность
у
в
плоскости
~
,
приче
1
вн
е
шняя
у
•
х
#.
"fj
l
г
-nll
оско
ст
ь
t
·
пло
с
косmь
Р
ис
.
66.
Рис.
67.
область
ото
р
тил
долн\На
отоб
ражаться
во
впутреннюю
область
у
(рис.
66)
*.
КОllфОР
111
пр
образо
в
ан
и
е
описывается
выражепи
е
м
z
=
c
(++
el~
+
e2~2
+
...
+
e11~n).
(VI.11 )
Н
а
ПРИ~1
р,
z =
с
е-
-
~
~з
)
пр
обр
азует
«квадрат>}
(рис.
67)
о
сл
е
ГI
а
JIСКРИВЛ
ППЫ~Ш
торонами
и
за
нруглснпыми
углами
в
ОКР
'/
1
Н
ть
у.
Приписыв
ая
последующие
члены
к
правой
час
т
и
:)того
уравп
ПИЯ,
мы
МОЖ
J\I
0'1
НЪ
близко
п
дойти
и
форм
е
ква
д
рата
J[
п
лу<шть
каи
го
ди
о
f
алые
ра
д
иусы
при
вершинах.
П
усть
п а
груз
т,
а
1\
плftСТlIне
па
беСRоне'1НОСТИ
задается
КОМП
ЛeI<С
II
ЬШИ
пот
лцизла
lИ
<р*
(О,
"Ф
*
(
~
),
тогд
а
полпые
I\омп
ле
I
,
сuые
по
тенц
и
алы,
КОТОРЫ
д
олж
ны
быть
найдены
таким
образом,
чтобы
удовлеТD
ОРЯ
ЛОС
Ь
слов
и
е
по
НОНТУРУ
отверстия,
запишутся
в
виде:
где
<р
(~)
=
(р
*
(~)
+
<ро
(~);
,~(~)
=
"Ф*
(~)
+
"Ф
о
(~),
00
<ро
Ш
= ~
a
n
~n,
о
}
(VI.119)
(
1.120
)
•
Если
необ
ход
имо
ор
е
обра
зо
вани
е
па
вв
е
ШI1ЮIО
область
у,
можно
исполь
-
80в
ать
м
етод,
пока
за
ВIIЫЙ
в
задаче,
см.
с
тр.
123.
Н5

сз
уч
та
объемных
сил
т<раево
условие
по
I<ОПТУРУ
напряжен
ного отверстия па
основании
(VI.114)
пришr
1а
т
вид:
(VI.121)
Подставляя
J
омnлеI<сные
потенциалы
(VI.119),
П
l\
ii
д
м:
z
(о)
- , (
1)
- ( 1 ) -
10
+
.r.
fPo
(а)
+
;'
(-})
fPo
а
+
'Фа
-0- - 1 L
2'
(VI.122)
где
10
+
il~
= -
!fP*
(а)
+ z
(о)
<Р*'
(J.-
) +
'Ф*
(_1
)).
( 1.123)
1 _ -(1)
о
о
z' -
о
,
По
сл
едняя
в
ел
ичина
может
быть
вычислена
из
l1ЗВ
стных
1<0
ш
лсксных
потенциалов
fP*
(~)
и
'Ф*
Ш
}<аl<
ФУПlщия
от
а
.
Поэтому
из
уравнени
я
(VI.122)
BblT
el<aeT
эквивюrептно
тъ
~BYX
функций
от
cr
(или
от
б)
па
единичной
оr<ружпости,
и
сл
~
ват
льно,
мы
~10-
жем
прим
ПИТI,
теор
е
му
Гарнаl<а
(см
.
фОрt.fYлу
(2.19)
прнложевия
2)
,
:которая
заJ<лючается
в
том,
что
тожд
тво
111011
Т
быть
УМПОжево
1
do
па
-?
.•
--,.
,
где
~
ть
точка
внутри
у,
а
зат
м
проинтегриро-
_П'
О
-
~
вано
по
контуру
у.
Такой
результат
будет
ЭI<Dивалептпьш
с
( 1
.122),
но
так
иак
он
позволяет
ПРИМ
нять
методы
I<омплексного
1Iнтегрирования,
то
можем
определить
fPo
Ш
и
"Фо
(~).
ел
дова
тельво
из
(VI
.
12З)
_1_
S
<1'0
(о)
dcr
+ _ 1_ S
.::
(о)
~~
(-})
dcr
+
1
2ni
о
-
~
2ni
Z'(+)
o-~
v v
~
(VI.124)
+
2~'
S i'..
L~)
dcr
=
2~i
S
I
~
+
i~
dcr.
I
o-~
v
l'
I
П
ервый
интеграл
левой
части
па
ОС\Jовапии
интегр
альной
фор
мулы Ко
ми
(СМ.
формулу
(2.12)
ПРИЛО;l
епи
я
2)
равен
fPo
(
~).
Так
как
;h
(_1
_) =
Ь
+
Ь
1
+
ъ;
+
".
ТО
тр
тий:
интеграл
ле-
'Уоо
о
о
оз
'
вой
части
равен
Ь
О
(СМ
.
формулы
(2
.17),
(2
.
18)
прИЛО>J
пия
2).
Таким
образом,
без
учета
постояпноii:,
},оторая
пе
ока
зы
ва
ет
ВJШЯПИЯ
н
а
напряжения,
ко"шлексный
потепциаJl
fPo
(~)
определим
(
16

из
выражения
.
~~(+)
аа
=
_1_
.
S
Ii
+
ifz
da. (Vl.125)
а-
~
2ш
(J
-
~
v
Возьмем
опряжепuую
фушщиlO
от
(VI.128)
И,
учитывая,
что
оа
= 1
получим:
- .
-;(+)
<Ро
l
+)
+ z'
(о)
CP~
(а)
+
'Фо
(а)
=
f~
-
if~
п
о
у.
(VI.126)
1
do
Умножим
:>то
выражепие
на
- .
--
и
2лi
o-~
окрулшости
у.
Получим
_1
5
<го(+)
da
_1
r.
;(~)
2ni
о
-
~
+ 2ni J z'
(о)
v v
проинтегрируем
по
.
~(o)
ао
+
a-~
+ _
1_
. S
'1>0
(о)
аа
=
_1_.
r
Ii
-
ifz
а
о.
2
ш
(J
-
~
2ш
J
(J
-
~
v v
П
РВЫll
интегра.'1
ранен
'Фа
(~).
суммы
да
т
постоянную
tPo
(О)
=
а
о
,
а
трети
й
Окончател
ЬПО
t 5 ;(f)
<p~(o)
1 S
2ni z'
(о)
.
(J
_
~
аа
+
'Фо
(~)
= 2ni
Ii
-
ifz
d (VI 1
')7
a-~
(1.
. - )
v v
ВычисшfВ
ИIIТ
гра
Ibl
( 1.125),
получим
значение
<ро
(~)
И,
испол.ь
зуя
его
в
(vI
.127),
пайдем
'Фо
(~).
После
определеuия
ПОЛlJЫ.х
:коьmлеI<СnЫХ
потеlщиалов
]\Оьтон
нты
напряжений
HaUAeM
из
(VI.107)
и
(Уl.Н1).
Читатель,
сравпnвая
подобпое
изложение
ыетода
Мусхелиш
вили
с
оригиналом,
зам
тит,
что
l\омбинация
напряж
ний
Ф
пе
является
тОЙ
же
велич.иноЙ,
что
у
Мусхелишвили
n
представителей
русской
ШF\ОЛЫ
вообще,
у
I\OTOpblX
эта
J<омбивация
записывается
иак
УУ
-
х";'
+ 2iXy,
т
..
-Фи
специаJIЬ
Н
ОГО
обозпач
IШЯ
дл.я
пее
11
им
тся.
OAnaI<o
настоящее
lIзложение
построено
такиы
обра
зом,
что
}{омп
leHC1Jbl
потепциалы
И,
ел
довательпо,
нраевые
усло
вия,
которым
они
удовл
творяJOТ,
остались
таними,
кан
у
Муе
хелишвили.
ПриводеllI
nel<oTopbl
случаи
примевеНЮf
этого
метода.
В
1\а
честв
е
п
рвого
при
мера
найдем решение
задачи
(уже
решенной
н
53.
Решения
для
областей
с
нруглыми
новту
ра
ми)
пластины
с
l<РУГЛЫМ
отверсти
еы,
радиуса
а,
под
дейс
твием
растягив
ающих
си
1.
117

А.
Нспаоряжсвпо
с
круглое
OTBepCTlle
в
пла
ТJlпе
под
дей
твие
I
растягивающих
СIIЛ
ДЛЯ
конформпого
отоБРЮJ
епия
ип
шп
ii
области
отвер
ст
ия
ра
диуса
а
в
плоск
ости
Z
ВО
внутр
ПЩОIO
область
еДИШfчноii
окрущнос
ти
У
в
ПЛОСI{ОСТИ
~
Н
обходимо,
чтобы
а
Z=T'
(VI.12 )
Растяжение
па
беСJ{опечности
задается
компл
RСIIЫМИ
потеп
циалаllШ
(V
I.85),
JtOTOPbl
в
выран
Н
ИИ
ч
рез
~
при
обретают
вид:
1
а
'1
а
'Р*
Ш
=
т
т
Т'
'Ф*
Ш
=
-"2
Т
у
'
(V
I.129)
На
основаlfИИ(VI.123)f~
+
if~
=+
Та(<1-
{)
И,
ТaJШМ
образом,
-
2йz
за;
из
(VI.125)
(Ро
(~)
+
2~i
f
(-
:3)
a
1
+(Jo
~
~
d<1
=
у
~
,;..
5 +
т,
fo_-;
-~+o
у
ШШ,
и
пользуя
иптегра
J
IЫ
(2.17), (2.1 )
прилощевия
2,
1
q>оШ
="2
Ta~.
(V
I.130)
Далее
из
(VI.127)
1 S 3
<P~
(о)
d 1 S +
Та
(+
-
о)
-2'
-
<1
--,.-
<1
+
'Фо
(~)
=
-2-'
а<1,
ш
0-",
Щ
а-
у у
где
функция
<1Зq>~
(<1
)
ЯВ
яетея
регулярной
в
области
у
и,
псполь
зуя
интеграл
Iоmи,
-
~3q>~Ш
+
~оШ
=
-+Ta~.
Отнуда
(VI.13
1)
Полные
комплеl{СlJые
потенциалы
теперь
равны:
'1
а
1 J
'Р(С)
=Т
Т
У
+"2
та
;
ф(~)
= -
+
T
T-+Ta~+
+
Та~
З,
(VI.132)
118

а
u
пло
I<OCTJJ
Z
1 1
a
~
ер
(z
) =
4"
Tz +
Т
Т
-z-
;
1 1
а
2
1
а'
, (z) = - - T
z--
T
-+-
T -
4 2 z 2 z
3'
]
(V
I.133)
что
согласу
тся
с
результатами
53.
Реш
ения
для
областей
с
круг
ЛЫМ
И
}(оптурами.
Пла
типы
болыпих
размеров
с
пепапряжеппым
нр
у
говым
отверсти
м
по
д
действием
растягивающих
сил
.
Б.
Н
с
наПРЯil\сnnо
е
нвадратно
отверстие
в
пластин
е
под
действие
1
растягивающих
сил
Используем
пре
о
бразовавие
z =
е
(+
_ +
~
з
)
,
(VI.134)
К
О
Т
ОРО
,
как
упоьmпалось
выше,
дает
хорошее
приближеnяе
к
к
вад
рату,
отображаемому
в
единичную
ОКРУЖНОСТЬ
у
.
Р
азме
р
5
d
(
с
м.
рис
.
67)
р
а
в
I:I
ЗС
И.
таКИ~f
образом,
величипа
е
JI10жет
быт
ь
nai1
Aena
для
д
аппог
о
Iш ад
рата.
В
э
том
с
л уч
ае
ер*
Ш
=
+
Те
(+
-+
~з
)
,
1j.J*
(~)
=
= _
+
Те
(.J
__ +
~
з)
.
(
1.1
3
5)
Сл
едовательно
,
и
з
(VI.12
3)
~
+
i~
= - +
Те
{ + -
2а
- +
0"
' +
З~3}
'
И
З
у
р
а
ВIl
lIИЯ
(VI.1
2-)
ПО
Л
УЧШf
1
<Ро
(~
)
+
:'пi
IJ 1]1 - 6
а
1
+
2~
+
ЗйЗ
...
о o
~
-
----
o
-
-
~
~
-
--
da +
Ь
о
=
з
'
20' + 1
v
=
+
T
c(2~
+
+
~
з
... ).
(V
I.136)
Ипт
грал
в
л
е
вой
части
может
быть
з
а
писав
в
виде:
2~i
.1(
~
- :3
)(
1 -
2~4
+
4~8
...
)
х
v
(
- +
2;;2
+
З
а
з
) do
Х
а
1
- 0 -
---ат-
...
~
,
119
