Фёршт Э. Структура и механизм действия ферментов

Подождите немного. Документ загружается.

ОСНОВНЫЕ УРАВНЕНИЯ ФЕРМЕНТАТИВНОЙ КИНЕТИКИ Ц1

Концентрация

субстрата, при которой v =-^

max

обозна-

чается /См и называется константой

Михаэлиса.

Обратите вни-

мание,

что при низких значениях [S], когда [S] -С Км,

S].

(3.3)

2. Интерпретация кинетических

параметров

для

односубстратных

реакций:

механизм

Михаэлиса — Ментен

В 1913 г. Михаэлис и Ментен, развив идеи

других

исследо-

вателей, предложили

следующую

схему:

*S *cat

E + S

=Р=*

ES -—»• ЕР. (3.4)

Каталитическая реакция состоит из

двух

стадий. Сначала

фермент и

субстрат

соединяются и образуют фермент-субстрат-

ный

комплекс ES. Предполагается, что эта стадия протекает

быстро и обратимо и не сопровождается какими-либо химиче-

скими

изменениями; фермент и

субстрат

удерживаются вместе

за счет сил физической природы. На второй стадии протекают

химические процессы, характеризующиеся константой скорости

первого порядка

(число оборотов).

Уравнение скорости выводится следующим образом. Из

уравнения (3.4) получаем

(3.5)

(3.6)

Далее, поскольку суммарная концентрация фермента [Е]

концентрация

свободного фермента [Е] связаны соотношением

[E] =

[E]

-[ES],

(3.7)

имеем

Е8

1-Т??Уп!г

(3-8)

(3.9)

Это уравнение идентично уравнению (3.1), где Кгл равна

константе диссоциации фермент-субстратного комплекса.

112

ГЛАВА

Концепция

фермент-субстратного комплекса является краеу-

гольным камнем ферментативной кинетики и лежит в основе

наших представлений о механизмах ферментативного катализа.

В честь ученого, который ввел это понятие, комплекс субстрата с

ферментом,

образованный без участия ковалентных связей, ча-

сто называют

комплексом

Михаэлиса.

Последующие

модификации

механизма

Михаэлиса

— Ментен

Не

следует

отождествлять уравнение и механизм, предло-

женные Михаэлисом и Ментен. Уравнение выполняется для

многих механизмов, механизм же не всегда согласуется с полу-

ченными

данными.

Механизм Михаэлиса — Ментен предполагает, что фермент-

субстратный комплекс находится в термодинамическом равно-

весии

со свободными ферментом и субстратом. Это справедливо

только в том случае, если в уравнении

(3.10)

ki «С k-\\

E+S

=f=fc

ES >- EP.

(3.10)

Случай, когда k

сравнима с k-\, впервые был рассмотрен

Бриггсом и Холдейном в 1925 г.

а.

Кинетика

Бриггса

—

Холдейна

[2]: Км > Ks

Вывести уравнение скорости для схемы

(3.10)

немного

труд-

нее,

чем для механизма Михаэлиса — Ментен. При расчете кон-

центрации

ES используется принцип стационарности, т. е. счи-

тается, что если измеряемая скорость реакции приблизительно

постоянна

в рассматриваемом промежутке времени, то [ES]

также постоянна:

0 = fti [E] [S] - *, [ES] _ *_, [ES] (3.11)

Из

уравнений (3.7) и

(3.11)

получаем

и,

поскольку v = k

[ES],

[E]

[S]*,

(3.13)

Это уравнение идентично уравнению Михаэлиса — Ментен (3.1);

здесь

*_,)/*,

= *«•

(3.14)

ОСНОВНЫЕ

УРАВНЕНИЯ

ФЕРМЕНТАТИВНОЙ

КИНЕТИКИ

ИЗ

Поскольку

константа диссоциации комплекса ES равна /Cs =

k-ilk

ТО

(3.15)

Естественно, что при k-i^ k

уравнение

(3.14)

сводится к виду

Км = Ks, т. е. константа Михаэлиса представляет собой в этом

случае

константу диссоциации фермент-субстратного комплек-

са.

б. Промежуточное соединение, образующееся вслед за

образованием ES: Км < Ks

Схему

Михаэлиса — Ментен можно использовать для анали-

за самых разных процессов, отличительной особенностью кото-

рых является образование в

ходе

реакции дополнительных ко-

валентно или нековалентно связанных промежуточных соедине-

ний.

Установлено, что во

всех

этих

случаях

применимо уравнение

Михаэлиса — Ментен, хотя теперь Км и k

t представляют собой

комбинации

различных констант скорости и констант равнове-

сия.

При этом

всегда

Км ^ Ks. Допустим, например, что реак-

ция

протекает с образованием ряда промежуточных соединений

[схема

(3.16)]

и конечная каталитическая стадия является мед-

ленной:

* К'

* /г, ,^\

E+S

^=? ES ч=* ES' <=* ES" -> ЕР, (3.16)

Медленно

где [ES']

=tf[ES],

a [ES"] = /C[ES].

Следовательно,

/(1

+ K + KK')

(3.17)

ffff

7(1+ * +

**').

(3.18)

Катализируемый химотрипсином гидролиз эфиров и амидов

протекает согласно

следующему

механизму:

Е+

=<=^=

ES ~^ ЕА -^*

ЕР

(3.19)

где ЕА — «ацилфермент».

Считая,

что концентрация комплекса ЕА стационарна, мы

можем записать

{№}

20)

114

ГЛАВА

г. е. получаем уравнение Михаэлиса — Ментен, где

*м =

*зУ(*2

+ *з)

(3.21)

*cat = W(*2 +

(3.22)

или

l/*

cat

= l/k

+ l/k

(3.23)

В более сложных случаях неравенство /См < /Cs может не вы-

полняться.

4. Все три механизма встречаются на практике

случае

механизма Бриггса — Холдейна, для которого

S> k-\, отношение

kcat/Км

равно k\ — константе скорости свя-

зывания

фермента и субстрата. В гл. 4

будет

показано, что

константы скорости связывания должны быть порядка

М^-С"

. Это позволяет сделать вывод, что для механизма

Бриггса — Холдейна отношение

kat/Км

равно ~10

—

М-

-с"

. Каталаза, ацетилхолинэстераза, карбоангидраза,

кротоназа, фумараза и триозофосфатизомераза — все эти фер-

менты по указанному критерию подчиняются кинетике Бриг-

гса— Холдейна, о чем свидетельствуют данные табл. 4.4. Еще

одним ферментом такого типа является пероксидаза, выделен-

ная

из хрена,— один из первых ферментов, к которому были

применены методы исследования быстрых реакций [3]. Сначала

пероксидаза образует с перекисью водорода компекс Михаэли-

са, который затем взаимодействует с донором водорода (реак-

ция

второго порядка). При достаточно высоких концентрациях

донора скорость второй реакции значительно превышает ско-

рость диссоциации комплекса Михаэлиса.

Образование вслед за фермент-субстратным комплексом

промежуточных соединений [как в

схеме

(3.19)

] —чрезвычайно

широко распространенное явление. Однако в

случае

физиологи-

ческих субстратов эти промежуточные соединения часто не на-

капливаются и медленной стадией в последовательности реак-

ций

(3.19)

является стадия с константой скорости k

. (Обуслов-

лено это причинами принципиального характера, обсуждающи-

мися

в гл. 10, где приведены соответствующие примеры.) При

этих условиях /См равна /Cs (константе диссоциации) и первона-

чально предложенный механизм Михаэлиса — Ментен оказыва-

ется всегда выполнимым. Для многих экспериментальных систем

наблюдается обратная картина. Исследователи часто использу-

ют в опытах синтетические высокореакционные субстраты; в этих

условиях часто происходит накопление содержащих ковалент-

ные связи промежуточных соединений.

ОСНОВНЫЕ

УРАВНЕНИЯ ФЕРМЕНТАТИВНОЙ КИНЕТИКИ 116

Б.

Физический

смысл

параметров

уравнения

Михаэлиса — Ментен

Смысл константы

cat

Когда имеется только один фермент-субстратный комплекс и

все стадии связывания достаточно быстрые, параметр k

t в

уравнении Михаэлиса — Ментен представляет собой просто

константу скорости первого порядка для химического превра-

щения

комплекса ES в комплексе ЕР. В более сложных ситуа-

циях

fecat является функцией

всех

констант скорости первого

порядка

и не может быть отнесена ни к какому конкретному

процессу, за исключением крайних случаев. Например, для ме-

ханизма Бриггса — Холдейна, когда комплекс ЕР диссоциирует

достаточно быстро, k

t = k

[уравнение (3.10)]. Однако если

диссоциация

комплекса ЕР протекает медленно, то константа

скорости этого процесса вносит вклад в параметр k

t и в

предельном случае, когда скорость диссоциации ЕР значительно

меньше скоростей химических стадий, параметр k

будет

ра-

вен

константе скорости диссоциации. Из рассмотрения схемы

(3.19)

видно, что в этом

случае

t является функцией констант

и k

. Однако если одна из этих констант много меньше другой,

cat

становится равной меньшей константе. Например, если

къ < h, то, согласно (3.22), A>

t = k

. Из этого

следует,

что k

не

может превышать ни одной из констант скорости первого

порядка

для реакционного пути в прямом направлении и пред-

ставляет собой, таким образом,

нижний

предел для констант

скорости химических реакций.

Часто параметр k

t называют

числом

оборотов

фермента,

поскольку он определяет максимальное число молекул субстра-

та, превращающихся в продукт одним активным центром в

единицу времени.

2. Смысл /С

: истинные и кажущиеся константы

равновесия

Несмотря

на то что Км равна /Cs — истинной константе дис-

социации

фермент-субстратного комплекса — только для про-

стого механизма Михаэлиса — Ментен или в аналогичных слу-

чаях, при решении определенных задач /См можно рассматри-

вать как

кажущуюся

константу

диссоциации.

Например, кон-

центрацию свободного фермента можно рассчитать из соотно-

шения

fE][S] ,„

ол

(

24)

116

ГЛАВА

где X [ES] — сумма концентраций

всех

фермент-содержащих

форм

Концепция

кажущихся

величин очень плодотворна и исполь-

зуется во многих

случаях,

например при определении р/С

. До-

вольно часто значения р/(а не отражают микроскопическую

ионизацию

данной группы, а представляют собой комбинацию

соответствующей константы с константами равновесия

между

разными

конформационными состояниями данной молекулы.

Эту

кажущуюся

константу можно определить титрованием как

простую константу рЛ*

. При анализе влияния температуры, рН

других

факторов на кажущуюся Д*м не

следует

слишком пола-

гаться на подобный упрощенный подход; необходимо помнить,

что константы скорости, функцией которых является кажущаяся

константа /См, также зависят от указанных факторов. То же

самое относится к значениям k

i- В литературе имеются при-

меры, когда наличие изломов на температурной зависимости

&cat объяснялось тем, что фермент претерпевает конформацион-

ные

изменения,

тогда

как в действительности имела место раз-

ная

температурная зависимость индивидуальных констант ско-

рости, входящих в параметр

at,

т. е. констант k

и k

в урав-

нении

(3.22).

То,

что /См является мерой количества фермента, связанного

той или иной форме с субстратом, иллюстрируется следую-

щей

схемой (сравните с механизмом действия химотрипсина):

E+S

=?=*

>•

ES' > Е + Р.

(3.25)

Применяя

условие стационарности к комплексу ES', получаем

[ES'] = [ES] kt/k

(3.26)

Когда

~^>k3,

[ES'] намного превышает [ES], так что ES' вно-

сит в /См больший вклад, чем ES, и является преобладающей

Любопытно, что кинетика Михаэлиса — Ментен может наблюдаться и

отсутствие насыщения фермента субстратом. Рассмотрим, например, сле-

дующую

схему:

Е + S —

~> Е' + Р,

I»

Здесь взаимодействие активной формы фермента с субстратом представляет

собой реакцию второго порядка; в

результате

образуются продукты и неак-

тивная

форма Е', которая медленно переходит в активную. Этот случай слу-

жит примером кинетики с кажущимся насыщением; при этом fccat = k

, a

Км = Да/*1. Если рассматривать Е' как

«связанную»

форму фермента, то

можно применять уравнение (3.24).

ОСНОВНЫЕ

УРАВНЕНИЯ ФЕРМЕНТАТИВНОЙ

КИНЕТИКИ

117

ферментсодержащей формой. Даже не решая написанных урав-

нений,

мы интуитивно

чувствуем,

что /См должна быть меньше

Ks приблизительно в ka/k

раз, т. е.

(3.27)

3. Смысл параметра

cai

Как

было показано ранее [уравнение (3.3)], скорость реак-

ции

при низких концентрациях субстрата определяется уравне-

нием

v =(k

cll

t/KfA) [E]o[S], т. е. отношение

kcat/Км

представ-

ляет собой

кажущуюся

константу скорости второго порядка.

Этот параметр не является истинной микроскопической кон-

стантой, за исключением крайнего случая, когда реакция лими-

тируется столкновением фермента с субстратом.

Ценность

параметра

kcat/Кгл

состоит в том, что он связывает

скорость реакции с концентрацией свободного фермента, а не с

его общей концентрацией. В этом нетрудно убедиться из рас-

смотрения

приведенного выше уравнения (3.3), поскольку при

низкой

концентрации субстрата фермент находится преимуще-

ственно в свободном состоянии ([Е]«[Е]о), и, следовательно,

скорость реакции есть

Ниже

будет

показано Сравнение (3.41)], что этот вывод спра-

ведлив для любой концентрации субстрата. Мы покажем также

[уравнение (3.44)], что параметр

t/Kn

определяет специ-

фичность

действия фермента при наличии конкурирующих суб-

стратов.

Отношение fe

t//(M не может превышать ни одну из констант

скорости второго порядка [4] для последовательности реакций,

идущих в прямом направлении, и представляет собой, таким

образом,

нижний

предел для константы скорости при связыва-

нии

фермента с субстратом.

В. Графическое представление данных

Для графического анализа данных и обнаружения отклоне-

ний

от идеальности весьма полезно преобразовать уравнение

Михаэлиса — Ментен в линейную форму. Чаще всего для этого

используют метод Лайнуивера—Бэрка. Взяв величины, обрат-

ные

правой и левой частям уравнения (3.1), и подставив выра-

жение (3.2), мы получим уравнение Лайнуивера—Бэрка [5]:

(3.28)

118

ГЛАВА

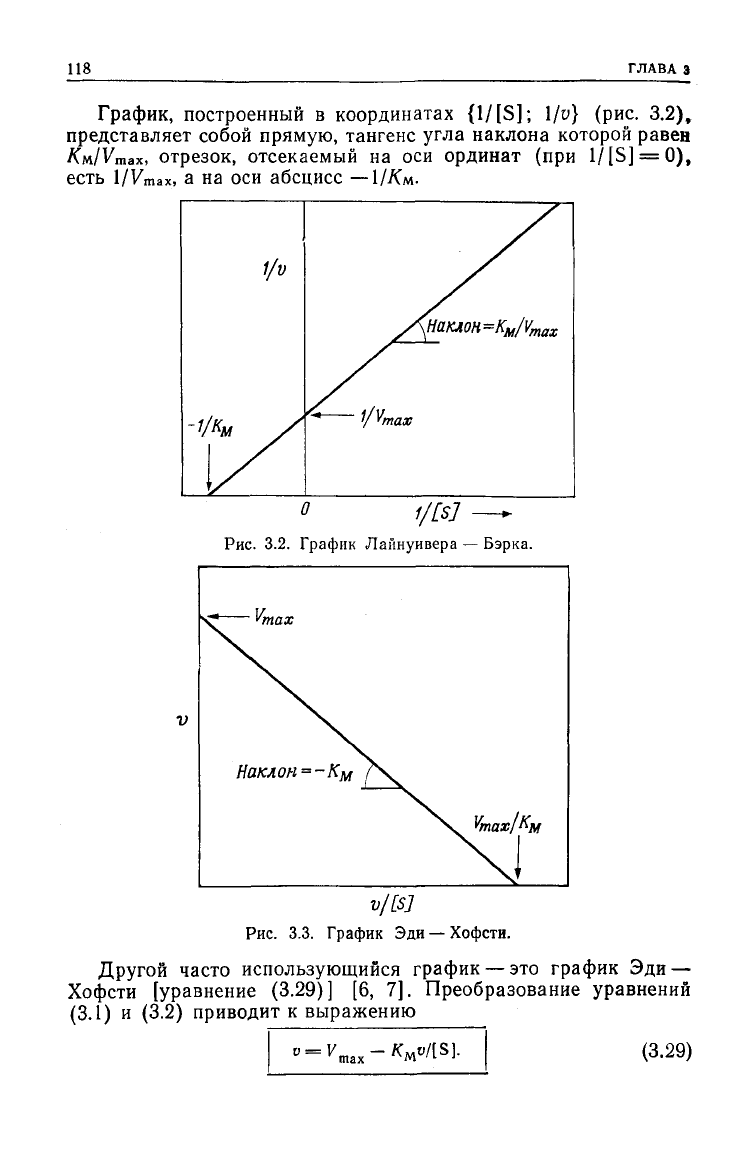
График,

построенный в координатах

{1/[S];

l/v} (рис. 3.2),

представляет собой прямую, тангенс

угла

наклона которой равен

/См/Vmax,

отрезок, отсекаемый на оси ординат (при 1/[S] = O),

есть

1/Vmax,

а на оси абсцисс —

1//См-

f/£

—+

Рис.

3.2. График Лайнуивера —

Бэрка.

v/[sj

Рис.

3.3. График Эди — Хофсти.

Другой часто использующийся график — это график Эди —

Хофсти [уравнение

(3.29)]

[6, 7]. Преобразование уравнений

(3.1) и (3.2) приводит к выражению

(3.29)

ОСНОВНЫЕ

УРАВНЕНИЯ ФЕРМЕНТАТИВНОЙ

КИНЕТИКИ

Ц9

График,

построенный в координатах

{y/[S];

v) (рис. 3.3),

представляет собой прямую, отсекающую на оси ординат (при

/[S] = 0) отрезок, равный Fmax. Тангенс

угла

наклона этой

прямой

равен —К/л, а отрезок, отсекаемый ею на оси абсцисс,

График

Лайнуивера —

Бэрка

имеет тот недостаток, что при

высоких концентрациях

субтрата

экспериментальные точки по-

падают на небольшой отрезок, в

результате

чего точкам, со-

ответствующим низким концентрациям, придается слишком

большой вес. Достоинство же этого графика состоит в том, что

он

позволяет просто оценить значение v при данной концентра-

ции

субстрата [S].

График

Эди — Хофсти лишен указанного выше недостатка,

однако

определить с его помощью значение скорости труднее.

Считается, что этот график

дает

более точные результаты, по-

этому для определения параметров Кгл и

исследователи

предпочитают пользоваться именно им [8, 9].

Г. Ингибирование

Помимо

необратимой инактивации ферментов при нагрева-

нии

или действии химических реагентов, может происходить

обратимое ингибирование в

ходе

нековалентного связывания

ингибиторов.

Различают четыре основных типа ингибирования.

1. Конкурентное ингибирование

Если

ингибитор I связывается с активным центром фермента

препятствует связыванию субстрата S и наоборот, т. е. I и S

конкурируют за связывание с активным центром, то говорят, что

является

конкурентным

ингибитором. Для простого механизма

Михаэлиса — Ментен [уравнение (3.4),

KM.

= KS]

следует

рас-

сматривать еще одну стадию:

Е =г=^ ES —^-»» Е + Р.

(3.30)

Используя при выводе уравнения скорости соотношение

[E]

= [ES] + [EI] + [E],

(3.31)

получаем

120

ГЛАВА

Конкурентное

1/v

v/[S]

f/[Sj

Бесконкурентное

v/[s]

Неконкурентное

v/[sj

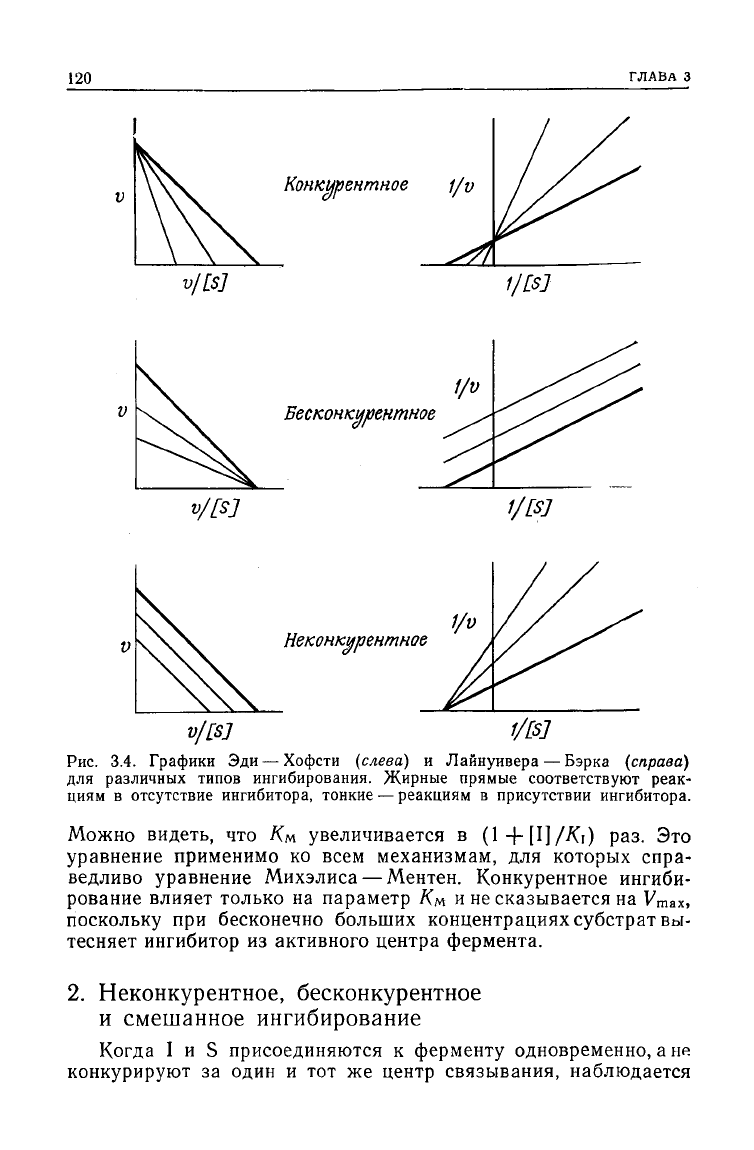
Рис.

3.4. Графики Эди — Хофсти

(слева)

и Лайнуивера — Бэрка

(справа)

для различных типов ингибирования. Жирные прямые

соответствуют

реак-

циям

отсутствие

ингибитора, тонкие — реакциям в присутствии ингибитора.

Можно видеть, что Км увеличивается в (1 -f-

[Ц/Ki)

раз. Это

уравнение применимо ко всем механизмам, для которых спра-

ведливо уравнение Михэлиса—Ментен. Конкурентное ингиби-

рование влияет только на параметр Км и не сказывается на

ах,

поскольку при бесконечно больших концентрациях

субстрат

вы-

тесняет ингибитор из активного центра фермента.

2. Неконкурентное, бесконкурентное

смешанное ингибирование

Когда I и S присоединяются к ферменту одновременно, а не

конкурируют за один и тот же центр связывания, наблюдается