Фёршт Э. Структура и механизм действия ферментов

Подождите немного. Документ загружается.

ИЗМЕРЕНИЕ

КОНСТАНТ СКОРОСТИ ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ 141

Рассмотрим пример, приведенный на рис. 4.6. Константа

скорости диссоциации комплекса тирозина с тирозил-тРНК —

синтетазой невелика, а потому константы скорости ассоциации

диссоциации удается измерить методом остановленной струи.

(Отметим, что иногда двухстадийный процесс можно ошибочно

принять

за рассмотренную выше одностадийную реакцию;

см.разд. 6.)

В тех

случаях,

когда

субстрат

в фермент-субстратном комп-

лексе не претерпевает химического превращения (например, в

отсутствие косубстрата в мультисубстратной реакции) или ко-

гда речь идет о связывании ингибитора, метод температурного

скачка является наиболее ценным методом определения кон-

стант скорости связывания лиганда.

3. Последовательные реакции

а.

Необратимые

реакции

Простейший случай последовательных реакций изображен

на

следующей схеме:

А -^> В -X С.

(4.28)

Используя уравнения материального баланса и способы ин-

тегрирования, примененные выше, нетрудно получить уравнения

для изменения концентраций А, В и С во времени:

[А]=-[А]

«р(-*,0.

[B] = [

А]о

*' (ехр (- Ы) - ехр (-

«2 — «1

[C] =

[A]

{h ехр (- kit) - k, ехр (

(4.29)

В — промежуточное соединение, которое образуется и затем ис-

чезает. Если

k\~5>k

то оно образуется с константой скорости k\,

а затем медленно распадается с константой скорости k

. Если же

&2»&ь

то В достигает стационарного уровня с константой ско-

рости ki и медленно распадается с константой скорости k\. Па-

радокс состоит в том, что промежуточное соединение кажется

образующимся с константой скорости его распада и распадаю-

щимся

с константой скорости его образования. Это легко понять,

проанализировав выражение для начальной скорости. При

&i<C&2 концентрация соединения В достигает стационарного

значения:

= o =

[A]-A

[B].

(4.30)

142

ГЛАВА

Стационарная концентрация В дается уравнением

[B]

]

(т. е.

<[А]

)

(4.31)

£>

= fc,[A]

. (4.32)

Отсюда

l/x = y

/[B]

= fe

. (4.33)

В последнем случае, когда k

> k\, концентрация В очень

низка,

а в первом, при k\ > k

, В накапливается. Эти два случая

можно дифференцировать, варьируя 1В].

1,0

0,8

0,6

0,4

0,2

Время,

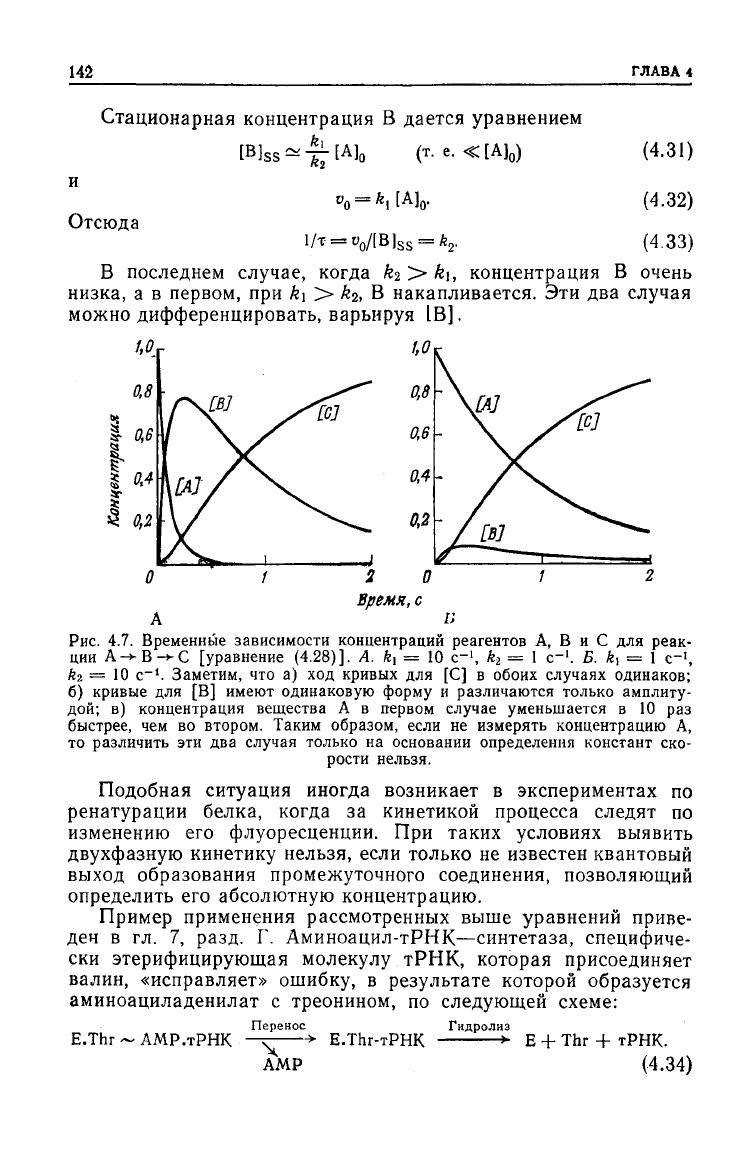
Рис.

4.7. Временные зависимости концентраций реагентов А, В и С для реак-

ции

А->-В-*С [уравнение (4.28)]. A. k, = 10 с"

, h= 1 с-

. Б. ft, = 1 с-',

= Ю с~*. Заметим, что а) ход кривых для [С] в обоих случаях одинаков;

б) кривые для [В] имеют одинаковую форму и различаются только амплиту-

дой;

в) концентрация вещества А в первом случае уменьшается в 10 раз

быстрее, чем во втором. Таким образом, если не измерять концентрацию А,

то различить эти два случая только на основании определения констант ско-

рости

нельзя.

Подобная ситуация иногда возникает в экспериментах по

ренатурации белка, когда за кинетикой процесса следят по

изменению его флуоресценции. При таких условиях выявить

двухфазную

кинетику нельзя, если только не известен квантовый

выход

образования промежуточного соединения, позволяющий

определить его абсолютную концентрацию.

Пример применения рассмотренных выше уравнений приве-

ден в гл. 7, разд. Г. Аминоацил-тРНК—синтетаза, специфиче-

ски

этерифицирующая молекулу тРНК, которая присоединяет

валин, «исправляет» ошибку, в

результате

которой образуется

аминоациладенилат с треонином, по следующей схеме:

E.Thr

АМР.тРНК

Перенос

AMP

E.Thr-тРНК

Гидролиз

Е + Thr + тРНК.

(4.34)

ИЗМЕРЕНИЕ

КОНСТАНТ СКОРОСТИ ФЕРМЕНТАТИВНЫХ РЕАКЦИИ 143

Как

будет

показано, скорость исчезновения E.Thr~ АМР.тРНК

можно прямо измерить по скорости образования AMP, концент-

рация

промежуточного соединения ЕЛЪг.тРНК определяется

непосредственно, а вторая стадия (гидролиз) исследуется неза-

висимо,

путем выделения неправильно этерифицированной

тРНК

и добавления ее к ферменту.

б.

Квазиобратимые

реакции:

стационарное

состояние

Более общим случаем ферментативной реакции является

процесс,

протекающий согласно следующей схеме:

Е *• ES' *• Е.

(4.35)

Например,

химотрипсин реагирует с п-нитрофенилацетатом

(AcONp) в соответствии с вышеприведенной схемой (когда для

первой стадии [AcONp] <C/(s) с образованием промежуточного

соединения

ацилфермента (ЕАс):

ft,

[AcONp]

Е —^ > ЕАс -^ > Е

(4.36)

HONp

AcOH

(для этой стадии k\ = )

Поскольку

ацилфермент постоянно образуется и распадает-

ся,

его концентрация является стационарной (при условии, что

[AcONp] S> [E]). Стационарная концентрация ацилфермента

задается уравнением

•±

[ЕАс] = 0 = Л,

[AcONp]

[E] - k

[EAc]

(4.37)

Далее, поскольку

[Е] + [ЕАс] = [Е]

(4.38)

О = ft,

[AcONp]

([E]

[ЕАс])

- k

[ЕАс]

(4.39)

ft,

[AcONp]

IE]. ,

44m

LbAcj

k2 + ki

[Ac0N

• ^-

Воспользовавшись уравнением начальной скорости

-ft,

[E]

[AcONp],

(4.41)

получаем

I/T

/[EAC]

(4.42)

-*2 +ft, [AcONp].

(4.43)

Точно

так же, как в случае обратимых реакций, промежу-

точное соединение образуется с константой скорости, которая

144

ГЛАВА

больше константы скорости превращения предшествующего

промежуточного соединения.

Аналитическое выражение для накопления во времени

HONp

имеет вид

[HONp]

= [Е]

(у^~) (т^Т^

ехр

[~ (*i

**)']}

+ v).

(4-44)

где £, = £,

[AcONp].

Если стадия ацилирования протекает в

условиях насыщения, то k\ =

eat

[S]/(/C

+ [S]V

В уравнении

(4.44)

имеется экспоненциальный член, стано-

вящийся

пренебрежимо малым при

/^,5т,

и линейный, дающий

в.конце

концов основной вклад в

iHONp].

в.

Последовательные обратимые реакции

Нахождение общего решения для этого случая мы отложим

до разд. 6. Здесь же рассмотрим ситуацию, когда одна из ста-

дий протекает гораздо быстрее другой. При таких условиях

времена релаксации для

двух

стадий существенно различают-

ся

и не налагаются

друг

на

друга.

Быстрой

является

первая

стадия (предравновесие)

*i[S] кг

*П?

^Г

(4-45)

Этот случай легко проанализировать, имея в виду два обсто-

ятельства: а) должны существовать два времени релаксации —

по

числу стадий; б) поскольку скорости этих стадий существен-

но

различаются, каждую из них можно рассматривать отдель-

но.

Первое время релаксации относится к стадии связывания.

Оно

задается уравнением, аналогичным уравнению (4.27):

(4.46)

Второе время релаксации относится к медленной стадии. Она

представляет собой обратимую реакцию, и по аналогии с урав-

нением

(4.19)

величина, обратная времени релаксации, пред-

ставляет собой

сумму

констант скорости прямой и обратной

реакций.

Однако эффективная константа скорости прямой реак-

ции

равна k

, умноженной на долю фермента, находящегося в

форме ES, т. е.

1/т

= k-

MS]

(4.47)

ИЗМЕРЕНИЕ

КОНСТАНТ СКОРОСТИ ФЕРМЕНТАТИВНЫХ

РЕАКЦИИ

145

где

*_i/*i.

(4.48)

Быстрой

является

вторая стадия. Приведенная выше ре-

акция

может служить примером индуцируемого субстратом

конформационного

изменения фермента (где ES' — просто дру-

гое конформационное состояние) или примером накопления

промежуточного соединения в

ходе

реакции. Следующая реак-

ция

дает

пример смещения равновесия

между

двумя конформа-

ционными

состояниями фермента, вызванного связыванием суб-

страта только одной из этих форм:

ES.

(4.49)

Такой

механизм имеет место при связывании лигандов с

химотрипсином; этот фермент находится в

двух

конформацион-

ных состояниях, но ароматические субстраты связывает только

одна из форм. Можно показать (разд. 6), что

(4.50)

Рассматриваемую ситуацию можно отличить от случая, ког-

да быстрой является первая стадия, поскольку

/тг

уменьшается

с увеличением [S]. Это легко понять, проведя аналогию с необ-

ратимыми и обратимыми реакциями [уравнения (4.1) и (4.10)].

Ясно,

что, когда концентрация S очень высока, реакция по

существу необратима, поскольку форма Е' полностью перево-

дится в форму ES и, следовательно, 1/т

стремится к k\. Анало-

гичным образом, когда

[S]-»-0,

концентрация ES становится

очень малой и

1/T2-V&I

+ k-\. Следовательно, время релаксации

зависит от концентрации.

4. Параллельные реакции

О параллельных реакциях говорят в тех случаях, когда соеди-

нение

одновременно

участвует

двух

или более реакциях. Такая

ситуация часто встречается в ферментативных реакциях, проте-

кающих с образованием активированного промежуточного со-

единения,

способного реагировать с несколькими конкурирую-

щими

акцепторами:

(

(4.51)

146

ГЛАВА

Кинетические уравнения

для

этого случая легко решаются

путем интегрирования, однако весьма полезно получить

их ре-

шения,

исходя

из

интуитивных соображений. Очевидно,

что

уменьшение концентрации вещества

определяется константой

скорости, являющейся суммой констант

и kc, а

скорость

образования соединений

В и С

пропорциональна отношению

соответствующей константы

сумме констант

и k

Поскольку

скорости образования

В и С

зависят

от

концентрации

А, оба эти

соединения должны образовываться

константой скорости,

равной константе скорости

их

исчезновения. Следовательно,

[A] =

[А]

ехр[-(*

)<],

(4.52)

] = J^5- {1 - ехр [- (й

+ k

) t]},

(4.53)

в "•"

[А]„ k

Ю -

feB

+ k

ft ~

exp

[~ (

B +

}•

(4-54)

Как

и для обратимых реакций [уравнение (4.10)], время

релаксации представляет собой

сумму

времен релаксаций для

двух

реакций.

Примеры параллельных реакций приведены в гл. 7 (атака

различными нуклеофилами ацилхимотрипсина, кинетика кото-

рой исследована в стационарных и предстационарных услови-

ях).

5. Вывод уравнений для метода температурного скачка

Рассмотрим в качестве иллюстрации связывание фермента с

субстратом, протекающее в одну стадию:

Е+

S ч=± ES.

(4.55)

Предположим, что вследствие изменения температуры происхо-

дит смещение равновесия, так что

[E] = [E]

+ e,

(4.56)

[S] = [S)

(4.57)

[ES] = [ES]

+ es,

(4.58)

где lE]eq, [S]

и [ES]

q — равновесные концентрации со-

ответствующих соединений при новой температуре.

[ES]/d*

([E]

+ в)

([S]

+ s) - *_,

([ES]

) =

(4.59)

l Иеч

[Sleq

~ *_,

[ES]

e(]

+ k

{

(

[E]

s +

[S]

e + в

•

s) - k^es.

(4.60)

Уравнение

(4.60)

можно упростить. Первые два члена в правой

части взаимно уничтожаются, поскольку в равновесии они рав-

ИЗМЕРЕНИЕ

КОНСТАНТ

СКОРОСТИ

ФЕРМЕНТАТИВНЫХ

РЕАКЦИЙ

147

ны.

Кроме того, так как реагенты сохраняются, е = s = —es.

А поскольку концентрация [ES]

q постоянна, d[ES]/dtf =

des/dt.

Следовательно,

des/dt

= ft, ([Е] es + [S] es + e • s) +

es.

(4.61)

Далее, если смещение равновесия невелико, членом второго по-

рядка малости, e-s, можно пренебречь. В таком

случае

уравне-

ние

(4.61)

удается проинтегрировать и найти время релаксации:

1/T«*,([E]

+ [S] ) + *_,.

(4.62)

Если равновесие смещается незначительно, то возвращение к

равновесию всегда является процессом первого порядка,

даже

если концентрации реагентов близки.

6. Общее решение для

двух

последовательных

обратимых реакций

Рассмотрим две последовательные реакции:

А ч=* В *=* С

(4.63)

-1

-2

В этом

случае

необходимо решить

систему

линейных дифферен-

циальных уравнений, что

даст

два времени релаксации:

1/Т

'/2(Р

<7),

(4-64)

1/т

= '/г (р —

я)<

(4.65)

где

(4.66)

q = [р

— 4 (k\ki -\- k—\k—i + k\k—г)\ •

Эти основные уравнения

могут

быть использованы во многих

случаях.

Весьма полезно выразить константы скорости в виде

сумм и произведений времен релаксации:

l/Ti + 1/Tj = ki + k-i +k

+ k-

I/T1T2

(4.67)

(4.68)

Эти уравнения легко решаются, если имеется концентраци-

онная

зависимость времени релаксации. Например, если реак-

ционная

последовательность представляет собой ряд превраще-

ний

псевдопервого порядка:

Е ^=L ES ф* ES', (4-69)

146 _ ГЛАВА 4

то ki в уравнениях (4.67) и (4.68) можно заменить Ha£[[S].Кроме

того, по аналогии с уравнением (4.62) для метода температур-

ного скачка, константу k] при исследовании релаксации можно

заменить на

£{([S]

+ [Е]).

Если

одно из времен релаксации много больше другого,

уравнения (4.67) и (4.68) упрощаются. Например, если первая

стадия протекает гораздо быстрее, чем вторая, то в уравнении

(4.67) членами 1/х

и (&2 + k-2) можно пренебречь. В этом слу-

чае Т2 определяется подстановкой (4.67) в (4.68). Для метода

температурного скачка получаем

1/T, = *[([E] + [S] ) + £_,, (4.70)

l/r Ь I M[E] + [S])

1/т

ki/k

+ {[E] + lS]y

(4.71)

Аналогичные выкладки можно провести и для последовательно-

сти

[S]

(4.72)

где первая стадия является медленной. В этом случае мы полу-

чаем:

ihi

= k_

([E]

+ [S]), (4.73)

k_A(k_Jk'

)

+ [E'])

Отметим два важных с практической точки зрения момента.

Кинетические

механизмы (4.69) и (4.72) можно различить, ис-

пользуя концентрационную зависимость 1/т

. Для механизма

(4.69) 1/тг при увеличении [S] возрастает, а для механизма

(4.72) — уменьшается. Однако в некоторых случаях провести

такую дифференциацию не удается. Например, если для меха-

низма

(4.72) [Е']3>[Е], то быстро образуется какое-то количе-

ство ES' с временем релаксации

%\,

затем по мере превращения

Е в Е' скорость образования ES' замедлится и процесс

будет

характеризоваться временем релаксации тг- Концентрационная

зависимость тг

будет

слабой, поскольку при [Е']!» [Е]

fti»fe_i

(рис.

4.8). В этой ситуации механизм (4.72) можно ошибочно

принять

за механизм (4.69), если в последнем количество обра-

зующегося ES' мало. Кроме того, при k-

~S>k

концентрационная

зависимость 1/т

для механизма (4.69) слабая. В обоих случаях

амплитуды изменений слишком малы, чтобы можно было точно

измерить константы скорости.

ИЗМЕРЕНИЕ

КОНСТАНТ СКОРОСТИ ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ

149

Более общий случай, с трудом поддающийся анализу,— это

двухстадийное связывание субстрата ферментом [схема (4.69)]

при

условии, что константа диссоциации для первой стадии,

100

[Профлавин],

мкМ

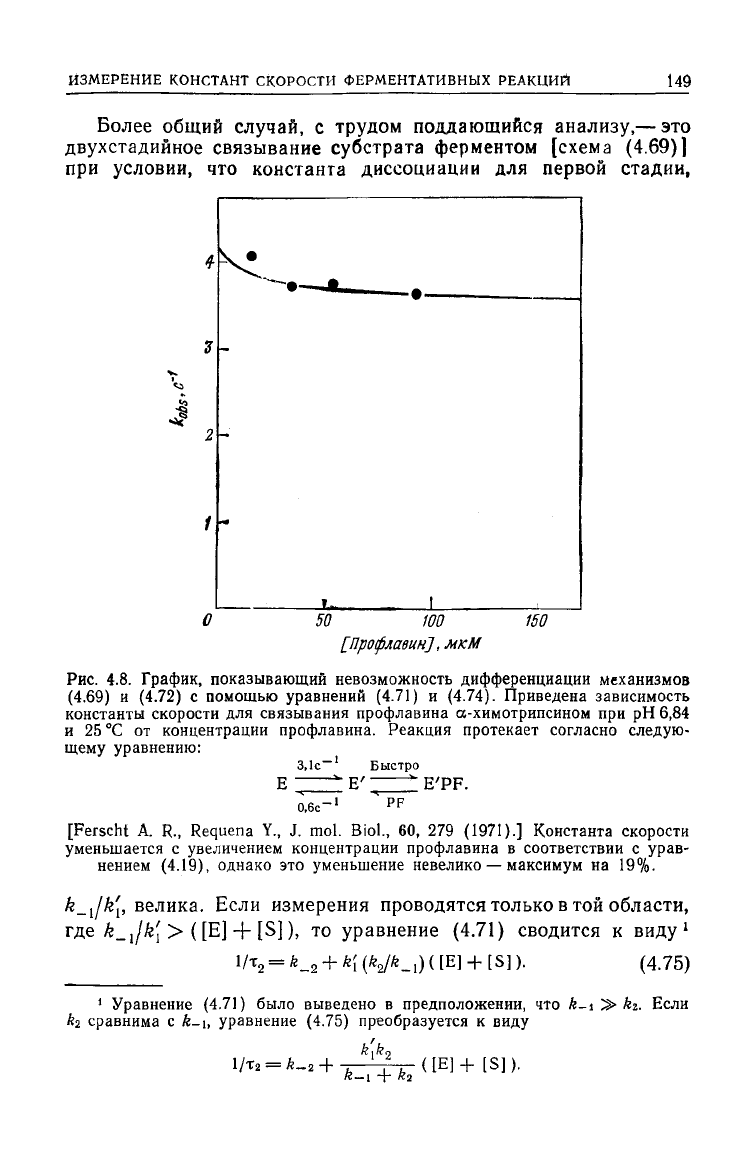
Рис.

4.8. График, показывающий невозможность дифференциации механизмов

(4.69)

и (4.72) с помощью уравнений

(4.71)

и (4.74). Приведена зависимость

константы скорости для связывания профлавина а-химотрипсином при рН 6,84

25 °С от концентрации профлавина. Реакция протекает согласно следую-

щему уравнению:

Б'"

E'PF.

0,6с"

[Ferscht A. R., Requena Y., J. mol. Biol., 60, 279

(1971).]

Константа скорости

уменьшается с увеличением концентрации профлавина в соответствии с урав-

нением (4.19), однако это уменьшение невелико — максимум на 19%.

/k[,

велика. Если измерения проводятся только в той области,

где k_

jk[ > ([Е] + [S]), то уравнение (4.71) сводится к виду

1/т

*_,) ([Е]

(4.75)

Уравнение

(4.71)

было выведено в предположении, что ft-i » кг. Если

сравнима с k-\, уравнение (4.75) преобразуется к виду

150

ГЛАВА

Данное выражение имеет такой же вид, как и для случая

простого одностадийного связывания субстрата ферментом

[уравнение (4.62)], что может привести к ошибочным выводам.

В этом

случае

расчет константы скорости связывания

дает

k[(k

/k_

т. е. величину, меньшую истинной константы скоро-

сти k\. Занижение значений некоторых констант скорости

[£J+£SJ,MM

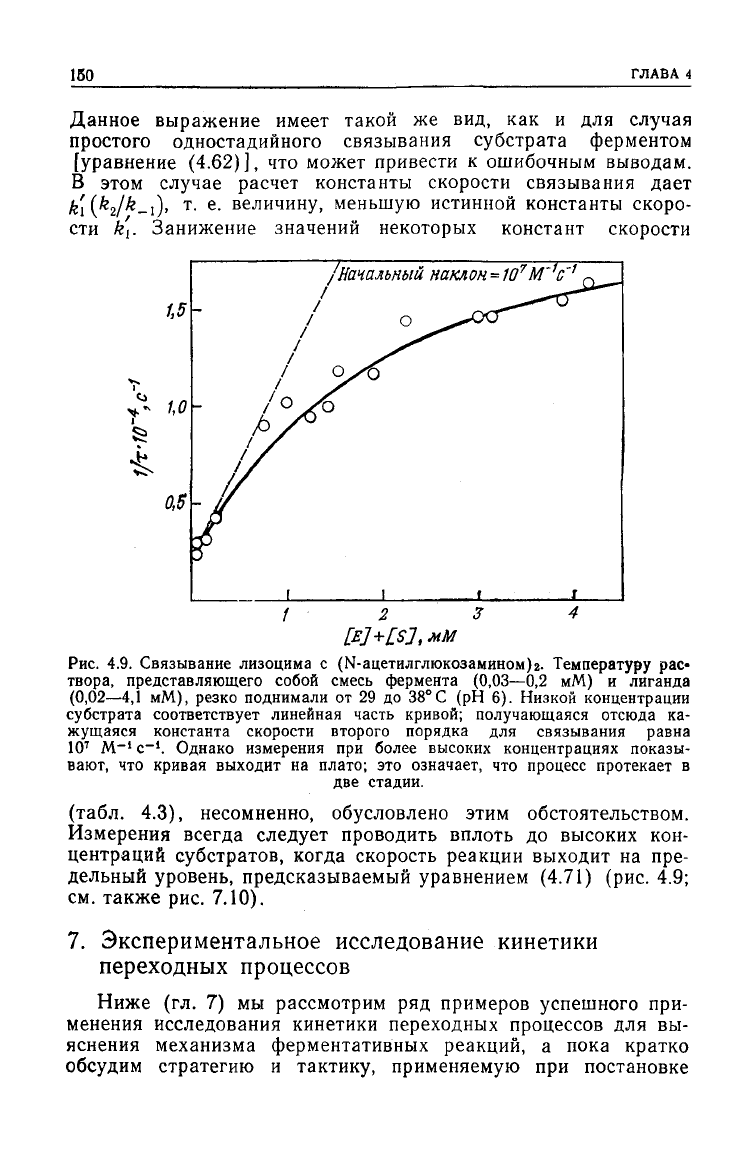
Рис.

4.9. Связывание лизоцима с (Ы-ацетилглюкозамином)г.

Температуру

рас-

твора, представляющего собой смесь фермента (0,03—0,2 мМ) и лиганда

(0,02—4,1 мМ), резко поднимали от 29 до

38°С

(рН 6). Низкой концентрации

субстрата соответствует линейная часть кривой; получающаяся отсюда ка-

жущаяся

константа скорости второго порядка для связывания равна

М~' с"

. Однако измерения при более высоких концентрациях показы-

вают, что кривая выходит на плато; это означает, что процесс протекает в

две стадии.

(табл. 4.3), несомненно, обусловлено этим обстоятельством.

Измерения

всегда

следует

проводить вплоть до высоких кон-

центраций

субстратов, когда скорость реакции выходит на пре-

дельный уровень, предсказываемый уравнением

(4.71)

(рис. 4.9;

см.

также рис.

7.10).

7. Экспериментальное исследование кинетики

переходных процессов

Ниже

(гл. 7) мы рассмотрим ряд примеров успешного при-

менения

исследования кинетики переходных процессов для вы-

яснения

механизма ферментативных реакций, а пока кратко

обсудим стратегию и тактику, применяемую при постановке