Фёршт Э. Структура и механизм действия ферментов

Подождите немного. Документ загружается.

ИЗМЕРЕНИЕ

КОНСТАНТ СКОРОСТИ ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ 131

ды, в то время как число оборотов большинства ферментов

составляет

—1000

-1

. Второй — метод

релаксационной

кине-

тики.

Проблема мертвого времени, связанного со смешиванием

реагентов, здесь

отсутствует

благодаря использованию предва-

рительно смешанных растворов.

А. Методы

быстрого

смешивания

реагентов

быстрого

«замораживания»

реакции

1. Метод непрерывной струи

В 1923 г. Хартридж и Роутон при исследовании присоедине-

ния

лигандов к дезоксигемоглобину применили метод непре-

рывной

струи [1]. Принцип этого метода иллюстрирует рис. 4.1.

Два шприца соединены через сместитель с реакционной трубкой.

Смеситель

t=l/x

Скорость

струн

— л;лс"'

^Субстрат

Рис.

4.1. Схема устройства, используемого в методе непрерывной струи.

Один шприц заполняется раствором фермента, другой — рас-

твором субстрата; оба раствора продавливаются с постоянной

скоростью и тщательно перемешиваются в смесителе, а затем

поступают в трубку и «старятся». При постоянной скорости

струи

«возраст»

раствора прямо пропорционален пути, пройден-

ному им в трубке, и скорости струи. Например, если скорость

струи равна 10 м-с-

, то на расстоянии 1 см от смесителя «воз-

раст»

раствора

будет

равен 1 мс, на расстоянии 10 см — 10 мс и

т. д. Скорость протекания струи

следует

поддерживать выше

критической,

чтобы гарантировать турбулентность потока. Ниже

этого критического значения, равного для трубки диаметром

мм приблизительно 2 м-с~', поток может стать ламинарным и

жидкость в центре трубки

будет

течь быстрее, чем у стенки. Тем

самым устанавливается верхний временной предел для трубки

данной

длины.

2. Метод остановленной струи

Этот метод был разработан в 1934 г. Роутоном [2] и значи-

тельно усовершенствован шестью годами позже Чансом [3].

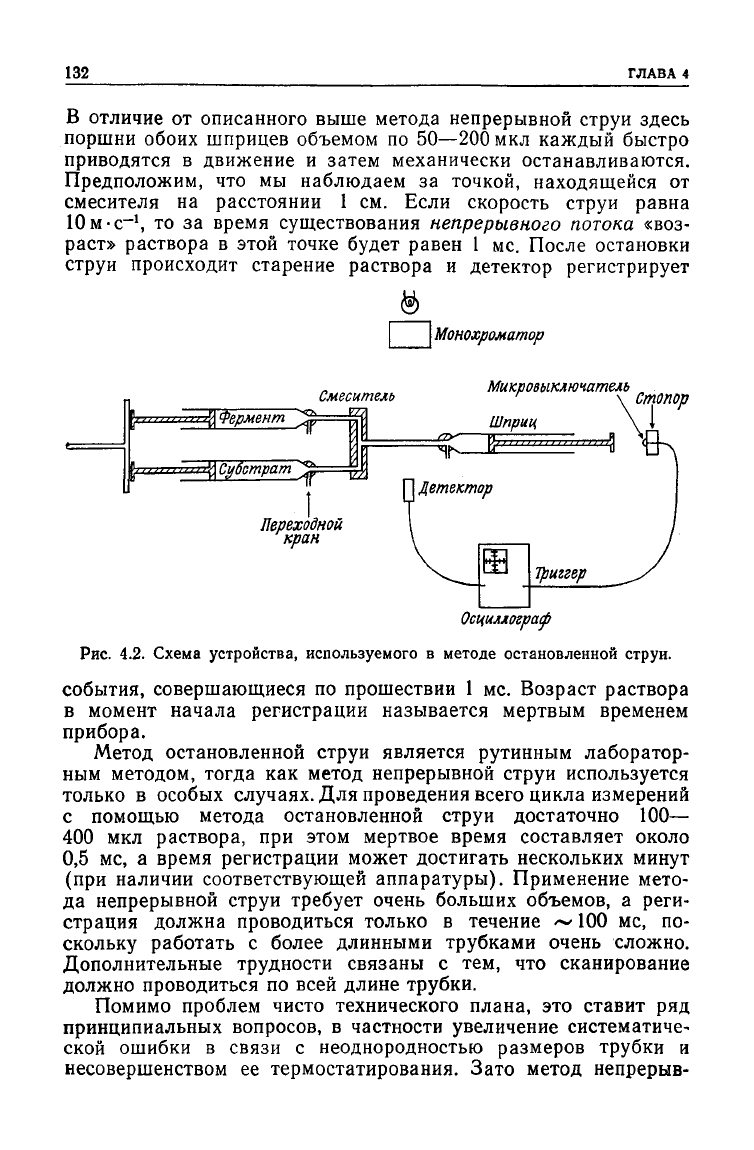
Лежащий в его основе принцип иллюстрирует рис. 4.2 [4].

132

ГЛАВА

В отличие

от

описанного выше метода непрерывной струи здесь

поршни

обоих шприцев объемом

по

50—200

мкл каждый быстро

приводятся

движение

затем механически останавливаются.

Предположим,

что мы

наблюдаем

за

точкой, находящейся

от

смесителя

на

расстоянии

1 см.

Если скорость струи равна

10м-с"

то за

время существования

непрерывного

потока «воз-

раст»

раствора

этой точке

будет

равен

1 мс.

После остановки

струи происходит старение раствора

детектор регистрирует

Монохроматор

Смеситель

Микровыключатель

Осциллограф

Рис.

4.2.

Схема устройства, используемого

методе остановленной струи.

события,

совершающиеся

по

прошествии

1 мс.

Возраст раствора

момент начала регистрации называется мертвым временем

прибора.

Метод остановленной струи является рутинным лаборатор-

ным

методом,

тогда

как

метод непрерывной струи используется

только

особых

случаях.

Для

проведения всего цикла измерений

с помощью метода остановленной струи достаточно

100—

400

мкл

раствора,

при

этом мертвое время составляет около

0,5

мс, а

время регистрации может достигать нескольких минут

(при

наличии соответствующей аппаратуры). Применение мето-

да непрерывной струи

требует

очень больших объемов,

реги-

страция

должна проводиться только

течение

~ 100 мс, по-

скольку работать

более длинными трубками очень сложно.

Дополнительные трудности связаны

с тем, что

сканирование

должно проводиться

по

всей длине трубки.

Помимо

проблем чисто технического плана,

это

ставит

ряд

принципиальных

вопросов,

частности увеличение систематиче-

ской

ошибки

связи

неоднородностью размеров трубки

несовершенством

ее

термостатирования. Зато метод непрерыв-

ИЗМЕРЕНИЕ

КОНСТАНТ СКОРОСТИ ФЕРМЕНТАТИВНЫХ РЕАКЦИИ

133

ной

струи имеет меньшее мертвое время — всего

100—200

мкс,

поскольку

отсутствуют

трудности, связанные с механической

остановкой

струи; остановка происходит за доли миллисекунды

может привести к возникновению ударных волн, если осуще-

ствляется слишком резко. Второе преимущество данного метода

состоит в том, что можно использовать инерционные детекторы,

так

как в каждой данной точке трубки возраст раствора посто-

янен.

Этот фактор играл особенно большую роль в эксперимен-

тах Хартриджа и Роутона, которые использовали в качестве

детектора ручной спектроскоп!

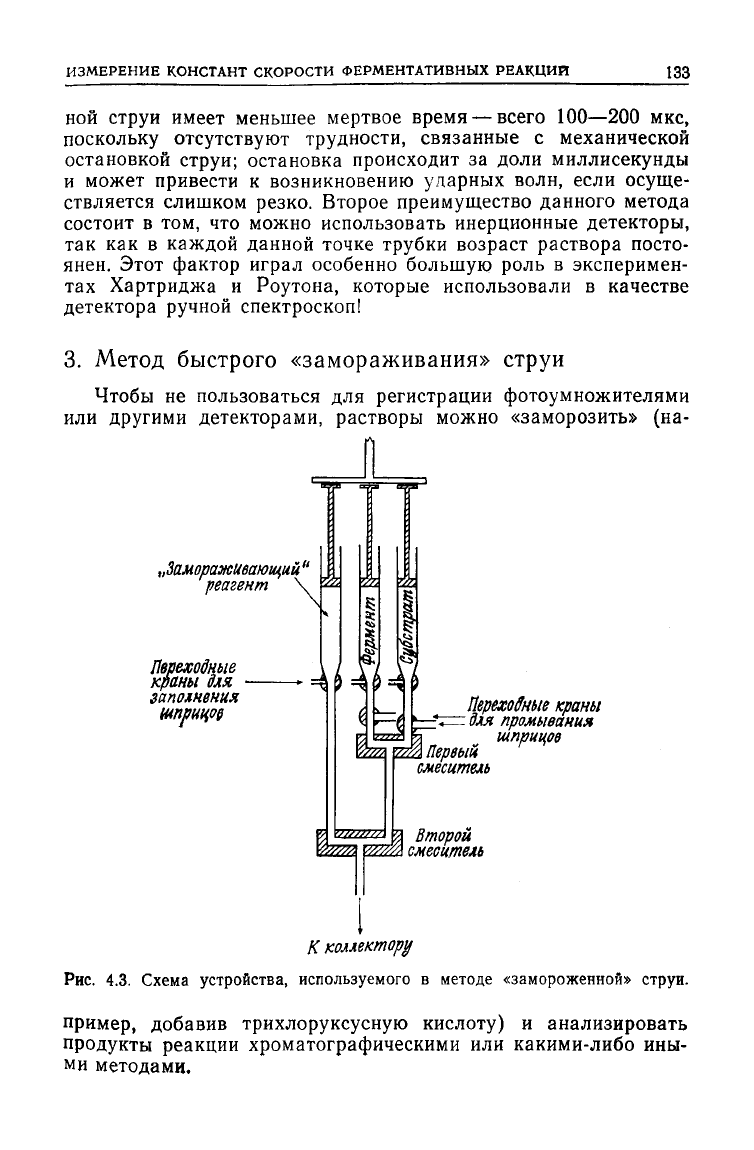
3. Метод быстрого «замораживания» струи

Чтобы не пользоваться для регистрации фотоумножителями

или

другими детекторами, растворы можно «заморозить» (на-

„Замораживающий

реагент

Переходные

краны

для

заполнения

Переходные

краны

i^r

для промывания

шприцов

Первый

смеситель

Второй

смеситель

коллектору

Рис.

4.3. Схема устройства, используемого в методе «замороженной» струи.

пример,

добавив трихлоруксусную кислоту) и анализировать

продукты реакции хроматографическими или какими-либо ины-

ми

методами.

134

ГЛАВА

а.

«Замороженная»

струя

В простейшем варианте этот метод состоит

в том, что

конец

реакционной

трубки, используемой

методе непрерывной струи,

погружают

сосуд

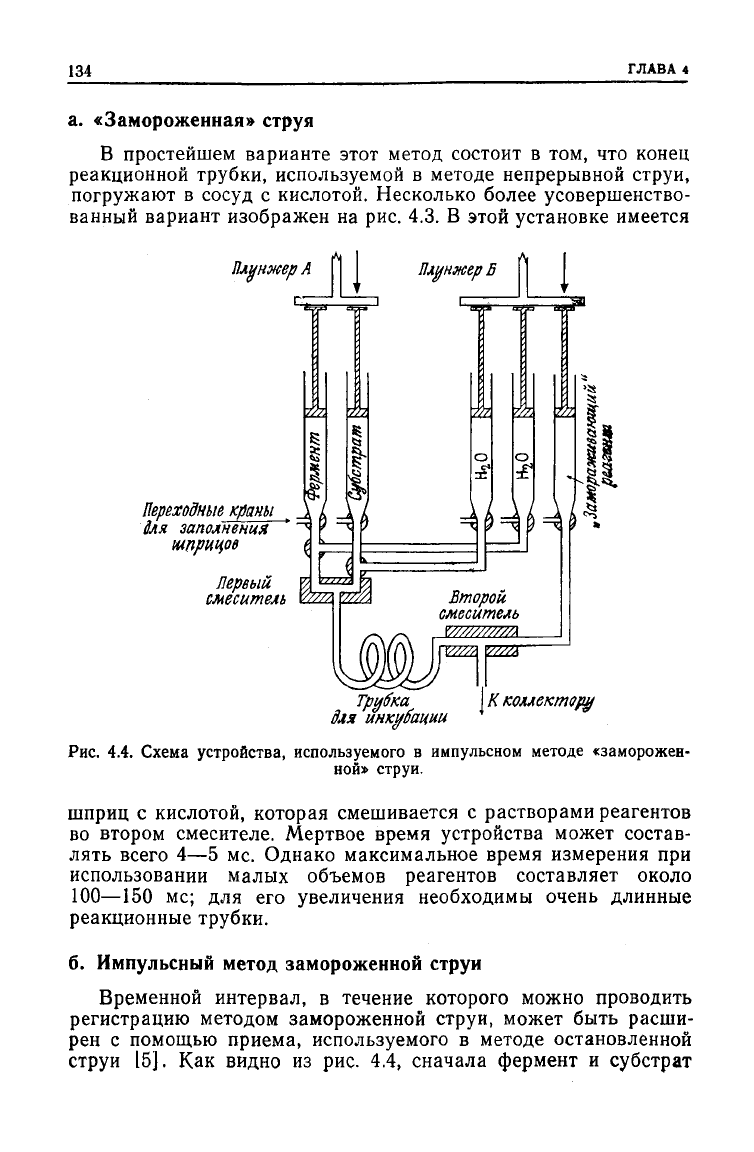
кислотой. Несколько более усовершенство-

ванный

вариант изображен

на рис. 4.3. В

этой установке имеется

Плунжер

Переходные

краны

для заполнения

шприцов

Первый

смеситель

Трибка

\К

коллектору

для инкубации

Рис.

4.4.

Схема устройства, используемого

импульсном методе «заморожен-

ной» струи.

шприц

кислотой, которая смешивается

растворами реагентов

во втором смесителе. Мертвое время устройства может состав-

лять всего

4—5 мс.

Однако максимальное время измерения

при

использовании

малых объемов реагентов составляет около

100—150

мс; для его

увеличения необходимы очень длинные

реакционные

трубки.

б.

Импульсный

метод

замороженной

струи

Временной интервал,

течение которого можно проводить

регистрацию методом замороженной струи, может быть расши-

рен

помощью приема, используемого

методе остановленной

струи

15]. Как

видно

из рис. 4.4,

сначала фермент

субстрат

ИЗМЕРЕНИЕ

КОНСТАНТ СКОРОСТИ ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ

135

смешивают

переводят

инкубационную

трубку

плунжером,

приводимым

движение сжатым воздухом,

затем

по

проше-

ствии некоторого времени

(150 мс или

больше) инкубируемую

смесь вместе

порцией дистиллированной воды переводят

вто-

рым плунжером

во

второй смеситель,

где и

«замораживают».

Б.

Релаксационные методы

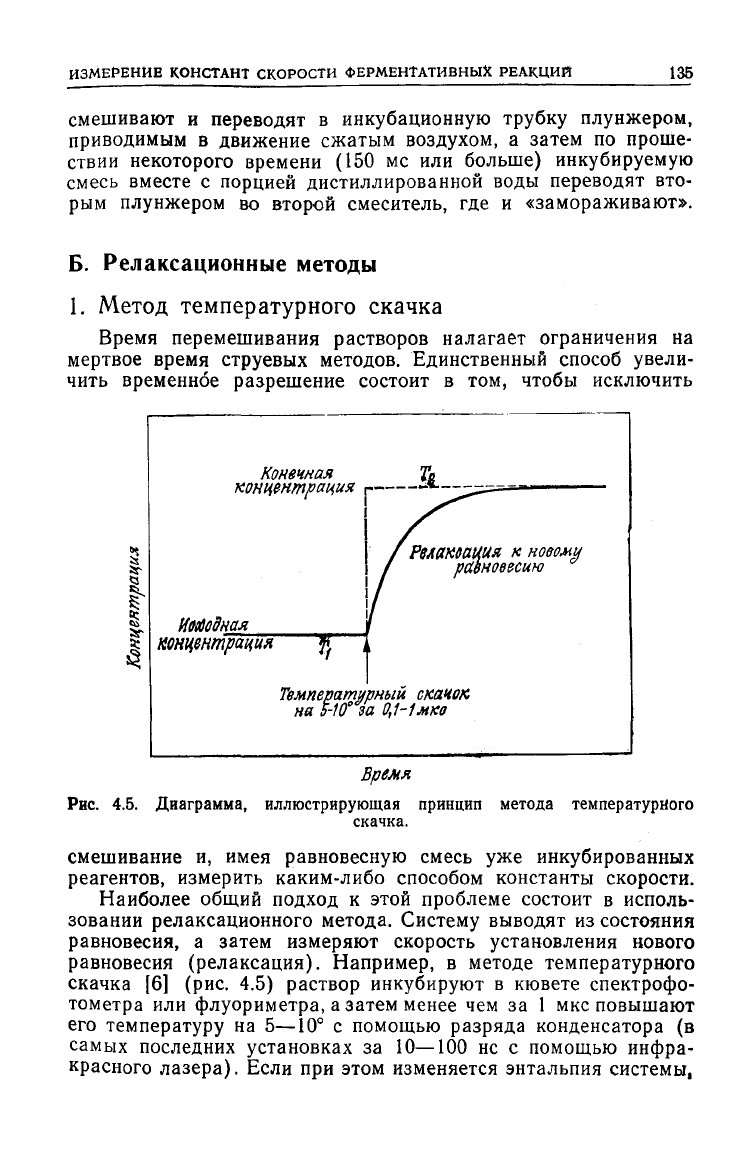
1. Метод температурного скачка

Время перемешивания растворов налагает ограничения

на

мертвое время

струевых

методов. Единственный способ увели-

чить временное разрешение состоит

в том,

чтобы исключить

Конечная

концентрация

ИШдная

концентрация

j» j

/Релаксация

новому

равновесию

•

Температурный

скачок

на

5-Ю

за

0,1-1мкв

Время

Рис.

4.5.

Диаграмма, иллюстрирующая принцип метода температурного

скачка.

смешивание

и,

имея равновесную смесь

уже

инкубированных

реагентов, измерить каким-либо способом константы скорости.

Наиболее общий

подход

этой проблеме состоит

исполь-

зовании

релаксационного метода. Систему выводят

из

состояния

равновесия,

затем измеряют скорость установления нового

равновесия (релаксация). Например,

методе температурного

скачка

[6] (рис. 4.5)

раствор инкубируют

кювете спектрофо-

тометра

или

флуориметра,

затем менее

чем за 1 мкс

повышают

его температуру

на 5—10° с

помощью разряда конденсатора

(в

самых последних установках

за

10—100

не с

помощью инфра-

красного лазера). Если

при

этом изменяется энтальпия системы,

136

ГЛАВА

то смещается и положение равновесия. Переход системы к но-

вому равновесию характеризуется в общем

случае

набором вре-

мен

релаксации т.

Ясно,

что к системам, в которых протекают необратимые

химические процессы, этот метод не применим. Наиболее ценен

он

для исследования простого связывания лигандов (например,

связывания

NAD+ с дегидрогеназой, связывания ингибиторов)

или

для исследования конформационных изменений в белке.

Предпринимались

попытки объединить метод температурного

скачка

с методом остановленной струи.

2. Ядерный магнитный резонанс [7—10]

Иногда

с помощью ЯМР можно измерить константы скоро-

сти

диссоциации

комплексов

между

ферментом и ингибитором.

В сочетании с константами связывания для данной реакции

это

позволяет получить константы скорости ассоциации.

В.

Анализ

предстационарной

кинетики

релаксационных

процессов

В простых случаях дифференциальные уравнения для меня-

ющихся со временем переходных процессов решаются относи-

тельно просто. Однако важно понимать,

почему

данному

случаю

соответствует именно данная форма решения. В настоящем раз-

деле

мы сосредоточим наше внимание на интуитивном

подходе

решению этой проблемы. Понимание сути вещей поможет нам

избежать ошибок в алгебраических выкладках, а кроме того, мы

сможем находить решение для некоторых сложных кинетиче-

ских

схем

просто по виду этих схем.

1. Простые

экспоненциальные

функции

а.

Необратимые

реакции

Предположим, что соединение А превращается в В с кон-

стантой скорости первого порядка k\ и эта реакция идет до

конца:

А -^ В. (4.1)

В таком

случае

-^--*,[А]

(4.2)

ИЗМЕРЕНИЕ

КОНСТАНТ СКОРОСТИ ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ

137

Интегрирование

уравнения (4.2)

дает

[A]

exp(-V).

где [А]

— начальная концентрация А. Поскольку

то

(4.3)

(4.4)

(4.5)

Как

[А], так и [В] являются простыми экспоненциальными

функциями.

Заметим,

что время полупревращения ti/, для реакции, в

которой

[А] = [В] = [А]

/2, задается уравнением

ехр (— kit) — -z-,

т. е.

М/2

0,6931

0,6931т.

(4.6)

(4.7)

б. Метод начальных скоростей

Рассматривая более сложные примеры, мы воспользуемся

методом

начальных

скоростей,

чтобы проиллюстрировать физи-

ческий

смысл некоторых выражений. Этот метод часто применя-

ется при изучении процессов, слишком медленных, чтобы ис-

пользовать полное время реакции, а также в том случае, когда в

системе протекают побочные реакции.

Начальная

скорость v

реакции (4.1) равна

»о

]

(4.8)

Константа

k\ определяется путем деления v

на ожидаемое

изменение'

концентрации реагента, следовательно,

[А]

(4.9)

в.

Обратимые реакции

В этом

случае

А превращается в В не полностью, а концент-

рация

А достигает равновесного значения.

А 4^ в.

(4.10)

При полном завершении реакции. —

Прим.

ред.

138

ГЛАВА

Для данной реакции

Л,

[А]

(4.11)

(4.12)

Подставляя выражение для [В] из уравнения (4.4), получаем

d[A]

([A]

-[AJ)

(4.13)

Это уравнение можно проинтегрировать, разделив переменные и

умножив каждую его часть на экспоненциальный множитель.

d [A]

—"п~—I"

fA] (ft,

•+•

к'Л = ft

[А]д, (4.14)

[A]

Отсюда

{[A] exp (ft, + ft

) t} = ft

[A]

exp (ft, + A

) t.

После

интегрирования получаем

[A] exp (ft, + ft

) t =

fe +

[A] exp (ft, + ft

) / +

const.

(4.16)

Используя начальные условия, состоящие в том, что при / = О

LA] = [А] о, а при t = оо равновесная концентрация A, (A]

есть

[A]

= [A]

/(ft

+ ft

), (4.17)

из

уравнений (4.4) и

(4.11)

получаем решение

[А]»

exp

(4.18)

Выражение (4.18) для изменения во времени концентрации реа-

гента А можно разделить на различные множители. Первый из

них — экспоненциальный член, который содержит константу

скорости, или — в терминах релаксационной кинетики — вели-

чину, обратную времени релаксации 1/т, равную

1/т - ft, + k

(4.19)

а второй —

амплитудный

фактор

(4.20)

ИЗМЕРЕНИЕ

КОНСТАНТ СКОРОСТИ ФЕРМЕНТАТИВНЫХ РЕАКЦИИ 139

Для обратной реакции, т. е. для реакции, в которой исход-

ным

веществом является В, а не А, можно записать

ехр

(*'

*Л

+ k

(

)

Время релаксации для этого выражения такое же, как и для

уравнения (4.18), но амплитудный множитель

иной.

Первый важный момент, который необходимо отметить, со-

стоит в том, что константа скорости для процесса приближения к

равновесию больше каждой из индивидуальных констант ско-

рости, kf и k

, и равна их сумме. Это легко понять, если проана-

лизировать выражение для начальных скоростей. Начальная

скорость в

случае

обратимой реакции

(4.10)

такая же, как и в

случае

необратимой (4.1), однако глубина последней реакции не

столь велика, как первой. Например, до заметного накопления

продукта В в системе

будет

присутствовать только реагент А,

следовательно, уравнение

o = *f tA]

останется в силе.

Однако суммарное изменение [А] определяется теперь урав-

нением

A[A]

[A]

-[A]

(4.22)

Подстановка выражения

(4.17)

дает

Л [А]

= [А]

*,/(*,+

(4.23)

откуда

1/т-

0о

/Д[А]

-*,

+ *,.

(4.24)

Второй момент состоит в том, что константы k\ и k

нельзя

определить, не зная амплитудный множитель.

Симметричность выражения для времени релаксации отно-

сительно констант скорости прямой и обратной реакций встре-

чается во многих

случаях,

и, как правило, константы скорости

мономолекулярных реакций нельзя рассчитать, не определив

предварительно равновесные концентрации А и В. Позже мы

увидим, что если реакция вследствие присутствия второго реа-

гента является не мономолекулярной, а псевдомономолекуляр-

ной,

то время релаксации

будет

зависеть от концентрации, что

позволит устранить указанную выше трудность.

2. Связывание

субстрата

с ферментом

E+S

3=* ES.

(4.25)

Если [S] ^?> [Е], то имеет место реакция первого порядка,

поскольку [S] меняется лишь незначительно. Если константу

скорости второго порядка для связывания фермента с субстра-

140

ГЛАВА 4

том обозначить через

, а

константу скорости

для

диссоциа-

ции

образующегося комплекса

—

через

ff,

то

уравнение

(4.25)

можно записать

более компактной форме:

(4.26)

Исходя

из

уравнения

(4.19),

получаем время релаксации

для

этой реакции:

(4.27)

Следует

отметить

два

момента:

а)

когда константы скорости

являются лсевдо'мономолекулярными, время релаксации зави-

сит

от

концентрации,

так что к

оп

и k

можно определить,

не

[Тирозин], мкМ

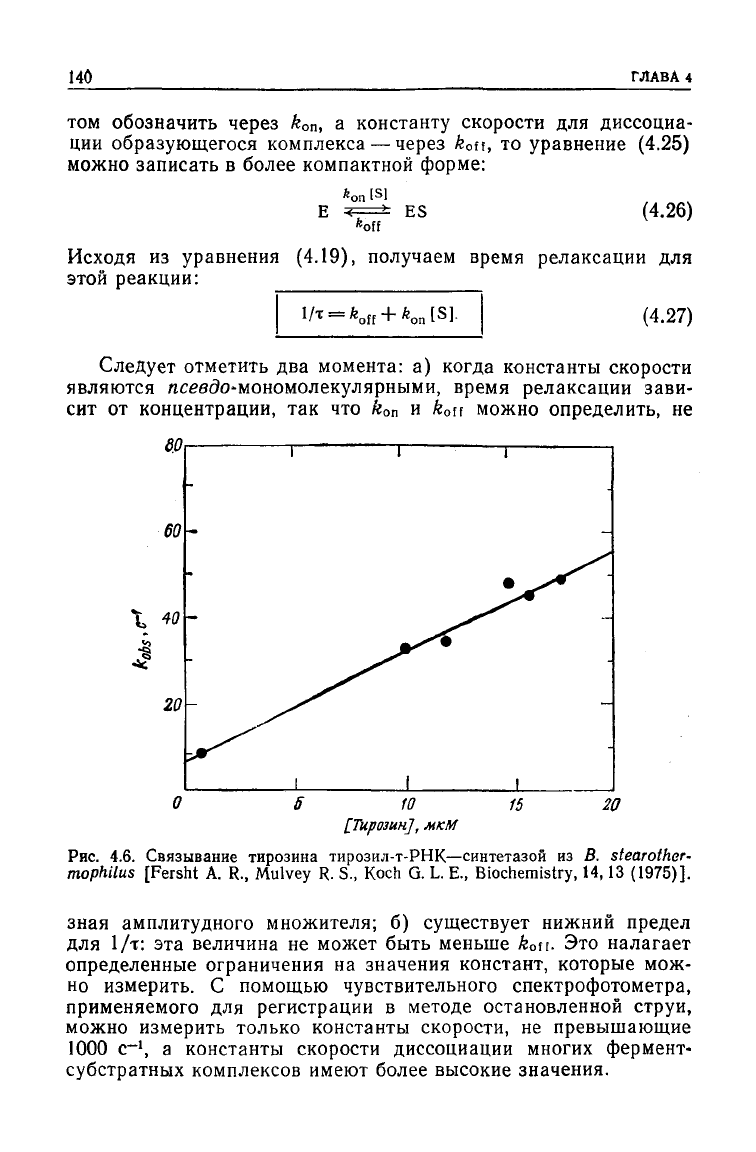
Рис.

4.6.

Связывание тирозина тирозил-т-РНК—синтетазой

из В. stearother-

mophilus

[Fersht

A. R.,

Mulvey

R. S.,

Koch

G. L. E.,

Biochemistry,

14,13

(1975)].

зная

амплитудного множителя;

б)

существует

нижний предел

для

1/т: эта

величина

не

может быть меньше

ft. Это

налагает

определенные ограничения

на

значения констант, которые

мож-

но

измерить.

помощью чувствительного спектрофотометра,

применяемого

для

регистрации

методе

остановленной струи,

можно измерить только константы скорости,

не

превышающие

1000

с~', а

константы скорости диссоциации многих фермент-

субстратных

комплексов имеют более высокие значения.