Федченко Г.М. Лекции. Численные методы
Подождите немного. Документ загружается.

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Следовательно,
В этой формуле в правой части участвует . Можно сначала вычислить
“грубое приближение” решения по методу Эйлера , а затем уточнить
Таким образом, мы получаем расчетные формулы метода Эйлера-
Коши:
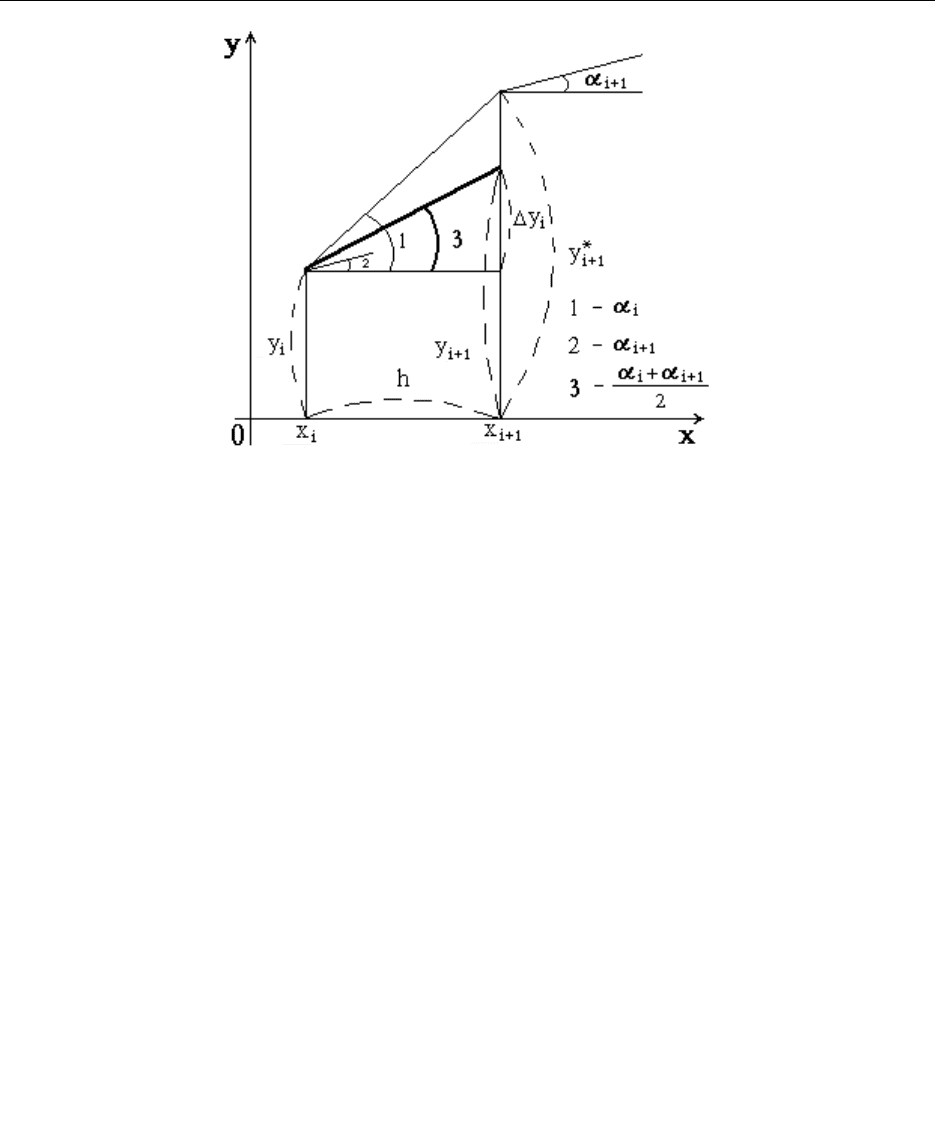
Геометрический смысл метода Эйлера-Коши
В этой модификации направление перехода из точки в точку
определяется другим способом. На каждом отрезке находим наклон
интегральной кривой в точке , также грубо вычисляем по методу Эйлера
значение , а затем определяем наклон интегральной кривой в новой точке
.
Затем находим среднее арифметическое наклонов в точках и и по
среднему наклону определяем приращение функции на всем отрезке ,
уточняя значение
149
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
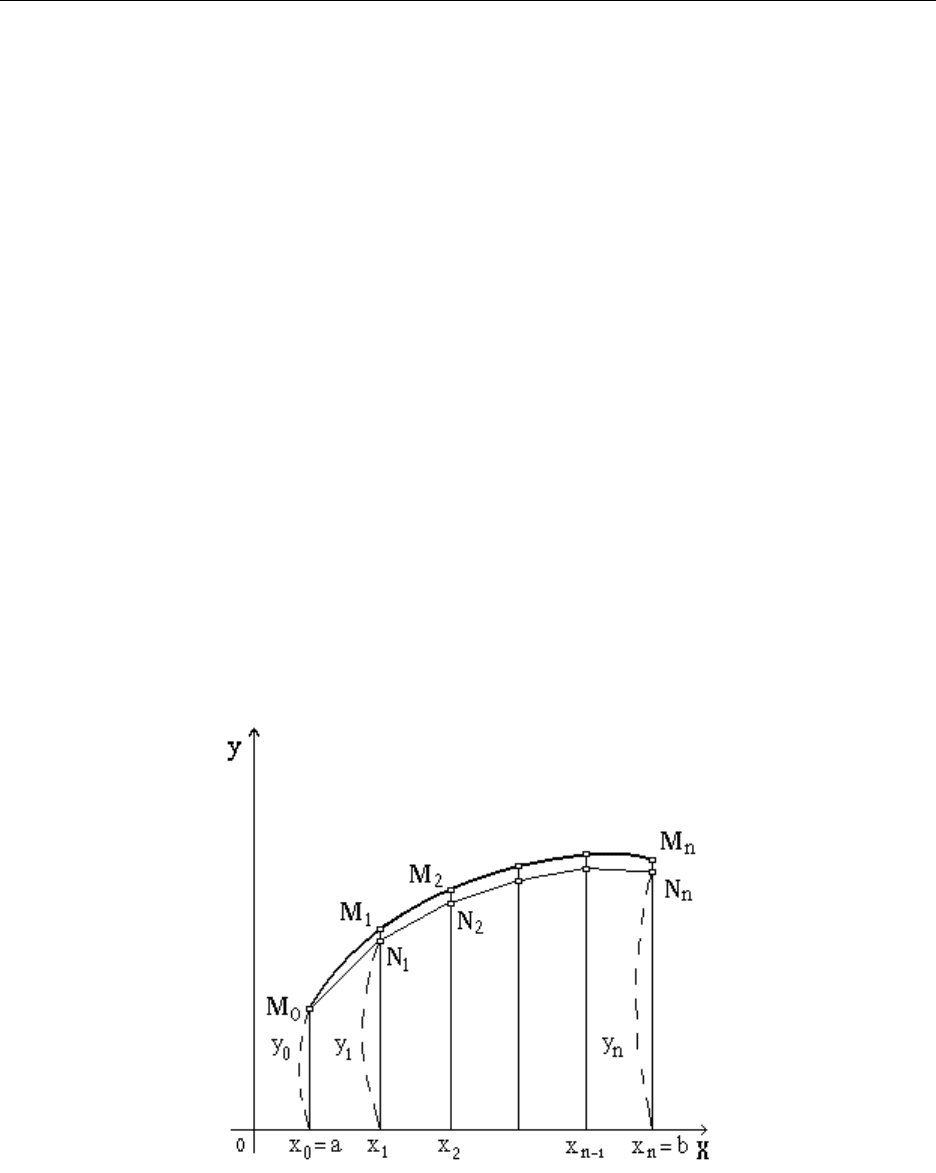
Таким образом, интегральная кривая M
0
M
1
M
2
...M
n
, где заменяется
ломаной M
0
N
1
N
2
...N
n
. Каждое звено ломаной на отрезке имеет усредненное
направление между направлениями касательных к интегральной кривой на
концах отрезка.
14.5. Контрольные вопросы и упражнения
1. Сформулируйте постановку задачи Коши и теорему существования и
единственности.
2. Сформулируйте подходы к численному решению задачи Коши.
3. Применяя метод Эйлера, найдите приближенное решение задачи Коши
в трех последовательных точках:
1 2 3
0.2, 0.4, 0.6x x x
и сравните с
точным решением
15.0 xey
x
5.1)0(y
xyy
4. Для задачи Коши выполните один шаг длины 0.1 по методу Эйлера-
Коши и оцените погрешность найденного значения по правилу двойного
пересчета.
5.1)0(y
xyy
150

МЕТРИКА. НОРМА. ОПЕРАТОР
Приложение 1
МЕТРИКА. НОРМА. ОПЕРАТОР
При решении рассматриваемых в курсе “Вычислительной
математики” задач вида y=A(x) искомый результат y будет представлять
собой либо числовую величину
8
, либо конечномерный числовой вектор
(векторную величину), либо действительную функцию (функциональную
величину). Например, числами являются действительный корень уравнения с
одним неизвестным и определенный интеграл, числовым вектором – решение
систем линейных алгебраических уравнений, функцией одной переменной –
решение обыкновенного дифференциального уравнения. Вычислительная
математика дает в наше распоряжение методы вычисления значения
величины =(), близкого в каком-то смысле искомому решению.
Мера близости между двумя какими-то объектами неразрывно связана
с понятием расстояния. Известно также, что расстояние может определяться
разными способами. Например, расстояние между двумя городами можно
измерить “по прямой”, а можно “по шоссе” или “по железной дороге” и т.д.
Расстояние, или, как еще его называют, метрика, является одним из
основных понятий математического анализа. Оно определяется с помощью
аксиом, согласующихся с обыденным представлением о расстоянии.
1.1. Расстояние. Метрическое пространство
Определение. Пусть X – некоторое непустое множество. Функция
, ставящая
в соответствие любым двум элементам x, yX число
(x, y) ≥ 0 с
выполнением условий
1.
(x, y) = 0 x = y (аксиома тождества);
2.
(x, y) =
(y, x) (аксиома симметрии);
3.
(x, y) ≤
(x, z) +
(z, y) (аксиома треугольника),
называется расстоянием, или метрикой, на множестве X. При этом число
#(x, y) называется расстоянием между x и y.
Множество X с введенной на нем метрикой
называется
метрическим пространством. На одном и том же множестве понятие
расстояния можно ввести разными способами. При этом получатся разные
метрические пространства.
1.2. Нормированное пространство
Частным случаем метрического пространства является линейное
нормированное пространство.
Определение 1.1. Непустое множество элементов произвольной природы X
8
Под числом далее всегда будем понимать действительное число.
151

МЕТРИКА. НОРМА. ОПЕРАТОР
называется линейным (векторным) пространством, если на нем
определены операции сложения элементов и умножения элемента на число
таким образом, что для любых элементов x, y, z X и любых чисел
,
R
x y X,
x X и выполняются следующие аксиомы:
1. x y = y x (коммутативность);
2. (x y) z = x ( y z) (ассоциативность сложения);
3.
X такой, что x
= x (существование нулевого, или
нейтрального, элемента
);
4. –x X такой, что x (–x) =
(существование противоположного
элемента –x);
5.
(
x) = (
) x (ассоциативность умножения на число);
6. 1 x = x;
7. (
+
) x =
x
x (согласование операций сложения и
умножения на число);
8.
(x y) =
x
y (согласование операций сложения и
умножения на число).
Определение 1.2. Линейное пространство X называется нормированным, если
каждому элементу x пространства ставится в соответствие действительное
число || x ||, называемое нормой, причем выполнены следующие аксиомы:
1. || x || 0;
2. || x || = 0 x =
;
3. ||
x || = |
| || x ||;
4. || x y || || x || + || y ||.
В линейном нормированном пространстве расстояние между двумя
элементами можно ввести как норму разности этих элементов:
(x, y) = || y – x ||, где y – x = y (–x)
Упражнение. Покажите, что при таком определении метрики выполняются все
аксиомы метрического пространства.
1.3. Норма и расстояние на множестве чисел
Пусть X = R, где R – множество всех действительных чисел с нормой
|| x || = | x |. Расстояние между x, y R определяется как модуль разности
между этими числами:
(x, y) = | y – x |.
Геометрически это расстояние равно длине отрезка, соединяющего
точки x и y на числовой прямой.
1.4. Норма и расстояние на множестве векторов
152

МЕТРИКА. НОРМА. ОПЕРАТОР
Пусть X = R – множество всех n-мерных числовых векторов и x = (, ,
…, ), y = (, , …, ) – два таких вектора. Расстояние между ними можно ввести
разными способами. Наиболее часто применяются следующие определения
норм и соответственно метрик:
норма-сумма
, ;
евклидова норма
, ;
норма-максимум
, .
Иногда к этим нормам применяют геометрические названия
кубическая, сферическая и октаэдрическая в соответствии с видом
поверхности, определяемой уравнением ||x||=const, когда x считается
переменным радиус-вектором в трехмерном пространстве.
Каждое из этих расстояний порождает свое метрическое
пространство. В частности, множество R с расстоянием
называется n-
мерным евклидовым пространством, а метрика
называется евклидовой.
Пример 1. Рассмотрим множество двумерных числовых векторов R и два
элемента этого множества x = (–1, 1) и y = (5, 3). Вычислим расстояние
между ними всеми тремя способами.
(x, y) = | 5 – (–1) | + | 3 – 1 | = 8,
(x, y) = = = 2,
(x, y) =max= 6.
Нетрудно убедиться, что расстояния между соответствующими
координатами векторов не превосходят расстояния между векторами при
любом способе его определения:
(x, y) (i=1, …, n).
Замечание. Все метрики, определенные на R эквивалентны, т.е. сходимость
последовательности по одной из них означает сходимость этой
последовательности и по другой метрике.
При оценке погрешностей векторов часто применяют расстояние
,
т.к. естественно связывать близость двух векторов с близостью их
соответствующих координат, а эта метрика делает это лучше, чем другие.
Очевидно, для ε>0
153

МЕТРИКА. НОРМА. ОПЕРАТОР
(x, y)≤ ε ε (i=1, …, n).
То есть два вектора удалены не больше чем на ε в смысле метрики
тогда и только тогда, когда все их соответствующие координаты отличаются
друг от друга не более чем на ε. Для других метрик это верно только в одну
сторону.
1.5. Норма и расстояние на множестве функций одной
переменной, непрерывных на отрезке [a, b]
C – множество функций одной переменной, непрерывных на [a,pb]p–
является линейным пространством.
Упражнение. Покажите, что Cявляется линейным пространством.
Пусть функции f и g определены и непрерывны на отрезке [a,pb].
Норму и соответственно расстояние можно ввести следующим образом:
, ;
, ;
, .
Упражнение. Найдите аналитически расстояние между заданными на отрезке
2
,0
функциями f(x)=x, g(x)=sinx.
1.6. Норма и расстояние на множестве квадратных матриц
размера nn
В линейном пространстве квадратных матриц размера nn наиболее
употребительны следующие нормы и соответственно расстояния (A=, B=):
, ;
, , где
– максимальное собственное число матрицы AA, C=B–A;
Замечание. Если матрица A – симметричная, положительно определенная, то
.
, ;
, .
Замечание. Все метрики, определенные в линейном пространстве квадратных
матриц размера nn также эквивалентны.
154

МЕТРИКА. НОРМА. ОПЕРАТОР
Пример. Рассмотрим множество квадратных матриц размера 22. Пусть
A= и B=.
(A, B) = ;
(A, B) = ;
(A, B) = .
1.7. Оператор
Определение 1.3. Под оператором A понимается отображение, т.е. правило,
по которому элементу x одного множества X ставится в соответствие
элемент y=Ax множества Y. Употребительна запись A: XY.
Пусть X, Y – линейные пространства, A – оператор, ставящий в
соответствие элементам x линейного подпространства пространства X
элементы yY.
Определение 1.4. Оператор A называется аддитивным, если
A(xx)=A(x)A(x) для x, x.
Оператор A называется однородным, если
A(x)=A(x) для x и R.
Оператор A называется линейным, если он аддитивен и однороден, т.е.
A(xx)=A(x)A(x) для x, x и , R.
Пусть X, Y – нормированные пространства.
Определение 1.5. Аддитивный оператор A: XY называется ограниченным,
если существует такая постоянная C, что при xX выполняется равенство
||Ax|| C||x||.
Наименьшая из таких постоянных C называется нормой оператора A и
обозначается ||A||. Таким образом, имеет место неравенство
||Ax|| ||A||·||x||,
которое называется условием согласованности норм.
Норма оператора A: XY, удовлетворяющая условию
согласованности норм, может быть получена с помощью норм пространств
X и Y на основе следующих равенств:
,
называемых условиями подчиненности норм.
Примером наиболее простого и важного для вычислительной
математики линейного оператора является линейное преобразование вектор-
столбцов пространства R в вектор-столбцы этого же пространства. Каждое
такое линейное преобразование y=Ax однозначно определяется nn
155

МЕТРИКА. НОРМА. ОПЕРАТОР
матрицей A вида
A = ,
которую можно отождествить с линейным оператором A: RR.
Замечание 1. Вышеназванные нормы линейного пространства квадратных
матриц размера nn согласованы с соответствующими нормами
пространства n-мерных числовых векторов:
норма с нормой ;
нормы и с нормой ;
норма с нормой .
Замечание 2. Для линейного преобразования A: RR справедливо
неравенство ||||A||, где – произвольное собственное число матрицы A, а ||
·|| – произвольная матричная норма.
1.8. Контрольные вопросы и упражнения
1. Продемонстрируйте геометрический смысл аксиом метрики, взяв
множество точек декартовой координатной плоскости, а в качестве
расстояния между двумя точками – длину отрезка, концами которого
являются эти точки.
2. Найдите множества чисел x R, удовлетворяющих условиям: а)
#(2,px)=0,5; б)
#(2,px)0,5; в)
#(2,px)>0,5. Изобразите эти множества на
числовой прямой.
3. Выясните геометрический смысл расстояний, определенных для
пространства двумерных числовых векторов R. Для этого рассмотрите
векторы a = (x, y), b = (x, y), которым на координатной плоскости xOy
соответствуют точки A(x, y) и B(x, y).
4. Для различных метрических пространств на множестве R, n-мерных
числовых векторов, постройте фигуры (n=2) и поверхности (n=3),
определяемые уравнением ||x||=1.
5. Выясните геометрический смысл расстояния
(f, g) для элементов
пространства C
6. Найдите геометрически и аналитически расстояние
(f, g) между
заданными на отрезке [0; 1] функциями f(x)=2–2x и g(x)=x.
7. На множестве квадратных матриц размера 33 посчитайте расстояния
,
,
для матриц A и B.
A= и B=.
156

ВВЕДЕНИЕ В ТЕОРИЮ ПОГРЕШНОСТЕЙ
Приложение 2
ВВЕДЕНИЕ В ТЕОРИЮ ПОГРЕШНОСТЕЙ
2.1. Приближенные числа. Абсолютная погрешность
Значение числовой величины, в истинности которого мы не
сомневаемся, называется точным. Часто, отыскивая значение какой-либо
величины, получают лишь ее приближенное значение. Например, степень
приближения измеряемых физических величин к их истинным значениям
зависит от совершенства применяемых при этом технических средств
измерения. В практике вычислений часто приходится иметь дело с
приближенными значениями чисел. Так, – число точное, но вследствие его
иррациональности при вычислениях можно пользоваться лишь его
приближенным значением. Рациональные числа нередко приходится
заменять их приближенными значениями. Так, вместо числа употребляют
близкую к нему десятичную дробь, например 0.2857.
Приближенным числом называют число, незначительно
отличающееся от точного и заменяющее его в вычислениях.
Пусть a– точное значение некоторой величины (как правило, оно
неизвестно), a – известное приближение к нему (т.е. приближенное значение
для a). Этот факт обозначают: a a или a a. Так 3.14 – приближенное
значение для : 3.14.
Определение 2.1. Разность a– a между точным и приближенным значениями
величины называется погрешностью приближенного значения a.
Определение 2.2. Абсолютной погрешностью приближения называется
модуль разности между точным и приближенным значениями
= | a– a |.
Как правило, точное значение величины – неизвестно. Поэтому
прибегают к оценке сверху расстояния между точным и приближенным
значениями.
Определение 2.3. Любое неотрицательное число (a), удовлетворяющее
неравенству
(a), (2.1)
называется верхней границей абсолютной погрешности (границей
абсолютной погрешностью) приближенного значения a.
Верхняя граница абсолютной погрешности определяется
157

ВВЕДЕНИЕ В ТЕОРИЮ ПОГРЕШНОСТЕЙ
неоднозначно. Если (a), то любое число, превышающее (a), также
будет верхней границей абсолютной погрешности. На практике стараются
выбрать возможно меньшее число, удовлетворяющее неравенству (2.1) и
именно его использовать для характеристики точности приближенных
значений. В дальнейшем верхнюю границу абсолютной погрешности будем
для краткости называть абсолютной погрешностью приближенного
значения.
| a– a | (a) a#–p(a) aOa#+p(a)
Следовательно, найдя приближенное значение a и его абсолютную
погрешность (a), мы определяем, что точное значение a располагается на
отрезке [a1–p(a);pa1+p(a)], т.е. находится “в пределах от a1–p(a)
доpa1+p(a)” (именно поэтому (a) называют предельной абсолютной
погрешностью). Для краткости пользуются записью a= a (a).
Пример 2.1. Точное значение числа =3.1415926… Определим абсолютную
погрешность числа a#= 3.14, взятого в качестве приближенного значения
числа . Абсолютная погрешность = | – a | = 0.0015926… В качестве
верхней границы абсолютной погрешности a можно взять число (a)=
0.0016: | – a |p p0.0016 или (a) = 0.002: | – a | p0.002 (запись более двух
значащих знаков в верхней границе погрешности бессмысленна и,
следовательно, безграмотна). Таким образом, 3.1383.142.p
Определение 2.4. Если известна абсолютная погрешность (a)
приближенного значения a величины a, то a называют приближением к aс
точностью до (a).
2.2. Относительная погрешность
Определение 2.5. Относительной погрешностью приближения a искомой
величины a (a0) называется неотрицательное число
= .
Так как точное значение величины aобычно неизвестно, его заменяют
приближенным значением и тогда:
= , (a0).
Определение 2.6. Любое неотрицательное число (a), удовлетворяющее
неравенству
(a), (2.2)
называется верхней границей относительной погрешности (границей
относительной погрешностью) приближенного значения a.
158
