Федченко Г.М. Лекции. Численные методы

Подождите немного. Документ загружается.

ВВЕДЕНИЕ В ПРЕДМЕТ «ЧИСЛЕННЫЕ МЕТОДЫ»

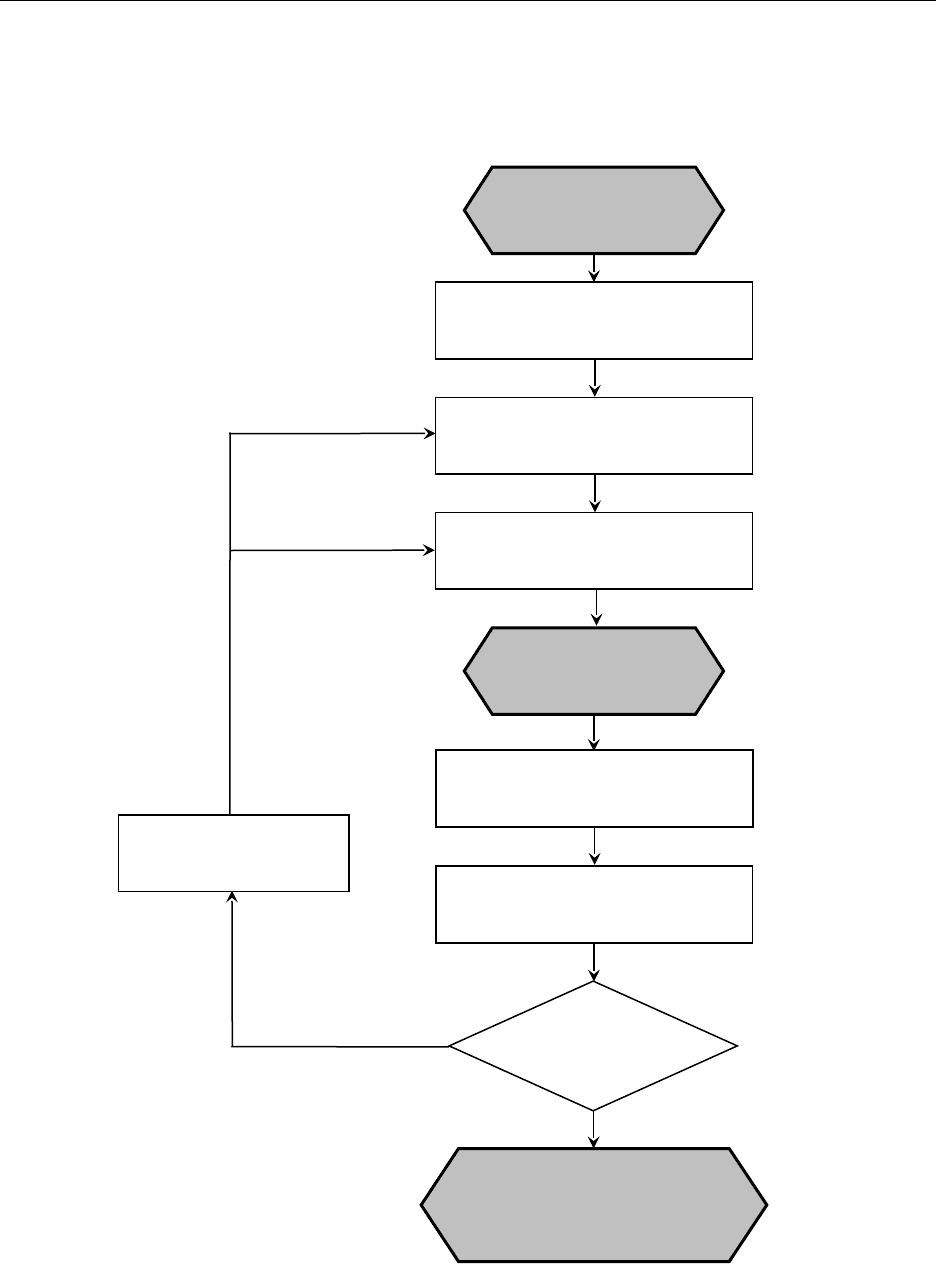
Общую схему процесса решения задачи методом математического

моделирования можно изобразить схематически:

Рассматривая математический анализ явления как теоретический

эксперимент, в процессе математического моделирования можно выделить

несколько этапов:

Исходный

объект

(процесс)

Определение

целей моделирования

Выделение

существенных свойств

Поиск

математического описания

Математическая

модель

Выбор

метода исследования

Проведение

исследования

Анализ

результато

Уточнение

модели

Действующая модель

для теоретического

эксперимента

ВВЕДЕНИЕ В ПРЕДМЕТ «ЧИСЛЕННЫЕ МЕТОДЫ»

 Определение целей моделирования и постановка задачи. Решение

практической задачи начинается с описания исходных данных и целей

моделирования. Целью может быть понимание устройства, структуры

объекта, явления, процесса; либо определение наилучших способов

управления объектом, процессом; либо прогнозирование последствий

реализации объекта, процесса. Точная формулировка условий и целей

решения задачи служит основой для математической постановки задачи.

Это наиболее важный и ответственный этап решения задачи, на котором

реализуется выбор общего подхода к ее решению, определяются

основные критерии, которым должна удовлетворять разрабатываемая

система и дается формальное математическое описание постановки

задачи. На данной стадии требуется глубокое понимание существа

задачи. В этой работе вычислительная машина не может оказать

практически никакой помощи.

 Построение математической модели. На этом этапе переходят от

абстрактной формулировки модели к формулировке, имеющей

конкретное математическое наполнение. Математическая модель

любого изучаемого явления, по причине его чрезвычайной сложности,

должна охватывать важнейшие для рассматриваемой задачи стороны

объекта (процесса), его существенные признаки и связи, подлежащие

формализации. Выделяя наиболее существенные характеристики

реального объекта, процесса, исследователь описывает их с помощью

математических соотношений. В этот момент модель предстает в виде

уравнения, системы уравнений, системы неравенств,

дифференциального уравнения или системы таких уравнений и т.д. Если

математическая модель выбрана недостаточно тщательно, слишком

грубо отражает взаимосвязи изучаемого явления, то какие бы

изощренные методы вслед за этим не применялись для поиска решения,

полученные результаты будут ненадежны, а в отдельных случаях и

совершенно неверны.

 Проведение математического исследования. На этом этапе

моделирования, в зависимости от сложности рассматриваемой модели,

применяют различные математические подходы к ее исследованию и

получению решения задачи. Например, доказательство теоремы

существования и единственности в определенном смысле решает задачу.

Однако, являясь зачастую неконструктивным, оно не позволяет решить

проблему изучения качественного поведения решения и оценки его

количественных характеристик.

Если это возможно, то математическая модель исследуется

аналитически. Аналитическое решение (т.е. представленное формулами,

выражающими результаты исследования через исходные данные)

обычно удобнее и информативнее численного, но зачастую его удается

получить лишь для наиболее грубых и несложных (в некотором смысле)

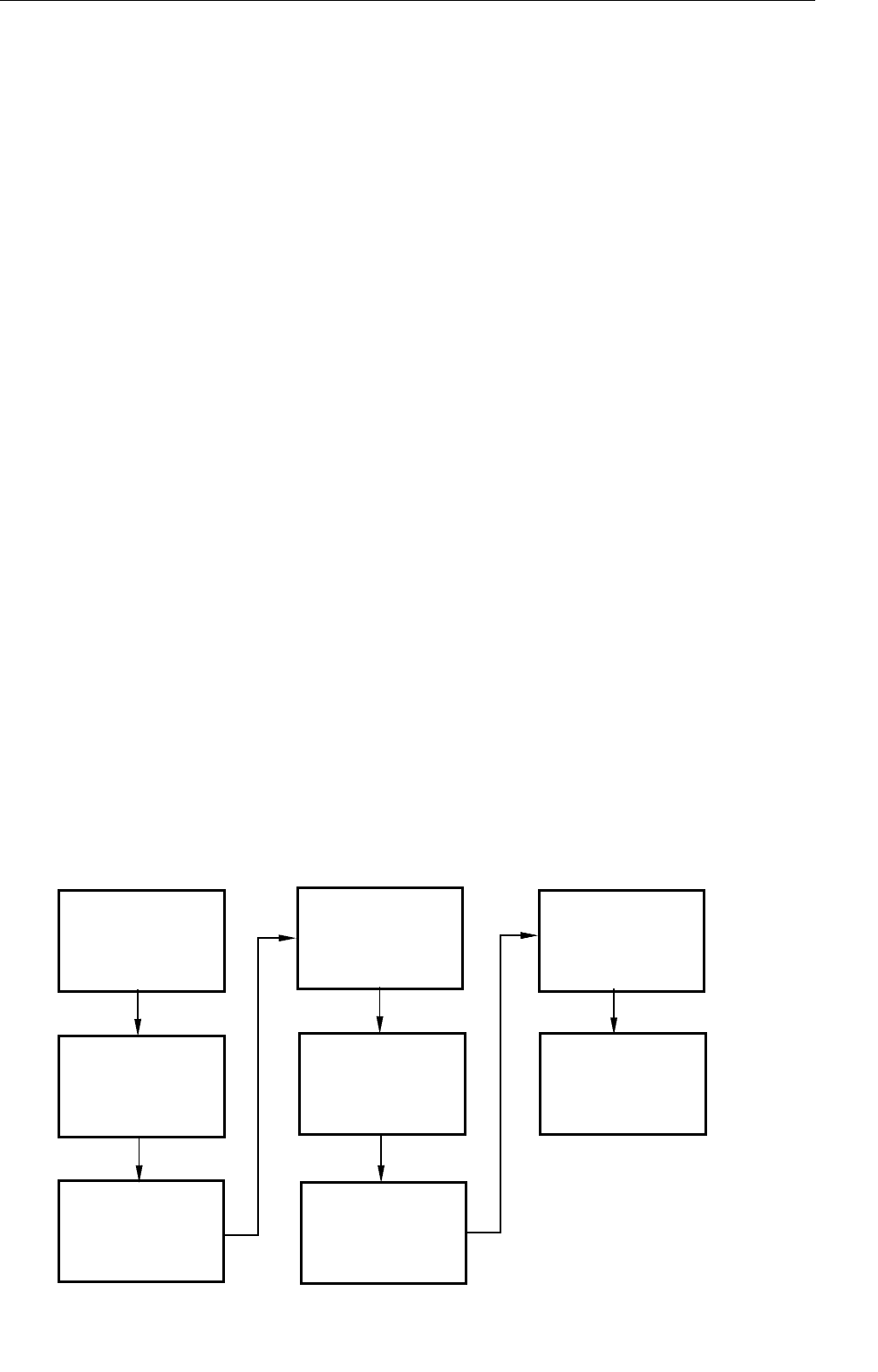
Вычислительные

эксперименты

4, Разработка

численного метода или

вычислительного

алгоритма

1, Постановка

задачи и определение

конечных целей

Интерпретация

полученных

результатов

5, Программирование

для ЭВМ

2, Составление

математических

моделей

Отладка

программы

3, Дискретизация

математической модели

Рис.1 Технологическая цепочка решения прикладных математических задач.

ВВЕДЕНИЕ В ПРЕДМЕТ «ЧИСЛЕННЫЕ МЕТОДЫ»

моделей. Точность этого подхода целиком зависит от порядка грубости

модели. Нередко такой подход позволяет оценить лишь порядок

величин. Следует отметить, что компьютеры при математическом

моделировании все чаще применяются для аналитических

преобразований. Использование средств символьных вычислений, таких

как REDUCE, MAXYMA, MAPLE, «интеллектуальных калькуляторов»

MATHEMATICA, MathCAD, MathLAB и пр., существенно

революционизирует это, традиционное для «бумаги и карандаша», поле

деятельности. Вместе с тем результат аналитического исследования

математической модели часто выражен столь сложными формулами, что

при взгляде на них не складывается восприятия описываемого явления.

Формулы нужно протабулировать, представить графически,

проиллюстрировать в динамике, т.е. проделать то, что называется

«визуализацией абстракций».

Для более точных и сложных моделей точное аналитическое решение

удается получить сравнительно редко. При теоретическом анализе

задачи в такой ситуации пользуются обычно приближенными

математическими методами, например разложением по малому

параметру, осреднением, изучением различных асимптотик и другими.

Эти приемы позволяют представить приближенное решение в

аналитической форме и с его помощью получить удовлетворительные

качественные и количественные результаты. Вышеназванные

компьютерные пакеты применимы для визуализации приближенного

аналитического решения.

Наконец для наиболее точных и сложных моделей основными методами

являются численные методы решения. Эти методы позволяют добиться

хорошего количественного и даже качественного результата в описании

модели. Но, правда, у них есть и принципиальные недостатки – как

правило, речь идет о рассмотрении некоторого частного решения.

Приведенная схема частично отражает обсуждаемые взаимосвязи:

Компьютер

Математическое исследование проблемы

Аналитические методы

Приближенные аналитические методы

Численные методы

Символьные преобразования

Численное решение

Визуализация абстракции

ВВЕДЕНИЕ В ПРЕДМЕТ «ЧИСЛЕННЫЕ МЕТОДЫ»

Можно увидеть, что любой из подходов к математическому

исследованию модели связан с использованием численных методов и

получением численного решения задачи. Использование при этом

компьютера требует такой интерпретации математической модели,

которая может быть реализована на компьютере – назовем ее

дискретной (вычислительной) моделью. Для реализации

вычислительной модели требуется разработка соответствующего

вычислительного алгоритма. Дальнейшая последовательность действий

– это программирование, отладка программы, вычислительный

эксперимент, интерпретация результатов расчета.

В рамках курса «Численные методы» мы остановимся на отдельных

проблемах численных методов при анализе сравнительно простых и

ставших классическими математических моделей.

 Анализ состоятельности модели. На этом этапе решается вопрос о

состоятельности математической модели и проведенного исследования,

т.е. осмысление результатов решения, сопоставление полученного

решения с имеющимися данными натурного эксперимента. Полученные

результаты подвергаются всестороннему анализу, на основании

которого, либо получается полный ответ для решаемой задачи, либо

выявляются некоторые особенности поведения исследуемого объекта,

требующие повторных экспериментов. При этом одни результаты могут

оказаться приемлемыми, а другие – противоречащими смыслу реальной

задачи; такие решения следует отбросить. Высшим критерием

пригодности полученных результатов в конечном счете является

практика. Хорошее согласование обычно свидетельствует о

правильности выбора модели. Модель адекватна реальному явлению,

если полученные характеристики совпадают с экспериментальными с

заданной степенью точности. В противном случае необходимы

дополнительные уточнения, изменения и повторение предыдущих

этапов исследования. Внесение изменений в постановку задачи

приводит к полному повторению всех перечисленных выше этапов

решения задачи.

1.3. История вычислительной математики

Раздел математики, имеющий дело с созданием и обоснованием

численных алгоритмов для решения сложных задач различных областей

науки, часто называют вычислительной математикой. В более узком

понимании вычислительная математика – теория численных методов

решения типовых математических задач. Главная задача вычислительной

ВВЕДЕНИЕ В ПРЕДМЕТ «ЧИСЛЕННЫЕ МЕТОДЫ»

математики – нахождение решения с требуемой точностью; этим она

отличается от классической математики, которая основное внимание уделяет

исследованию условий существования и свойств решения.

В истории вычислительной математики можно выделить три

основных периода:

1. 3-4 тысячи лет назад начался первый период. Он был связан с

ведением конторских книг, вычислением площадей и объемов,

расчетами простейших механизмов; иными словами – с

несложными задачами арифметики, алгебры и геометрии.

Исходные данные содержали мало цифр, и большинство выкладок

выполнялось точно, без округлений. Основное вычислительное

средство – ручной счет.

2. Второй период начался с Ньютона (XVIIв.). В этот период

решались задачи астрономии, геодезии и расчета механических

конструкций, сводящихся либо к обыкновенным

дифференциальным уравнениям, либо к алгебраическим системам

с большим числом неизвестных. Вычисления выполнялись с

округлением; нередко от результата требовалась высокая точность,

так что приходилось сохранять до 10 значащих цифр.

Вычислительные средства стали разнообразнее: таблицы

элементарных функций, затем – арифмометр и логарифмическая

линейка; к концу этого периода появились электромеханические

машины. Но скорость всех этих средств была невелика, и

вычисления занимали дни, недели и даже месяцы.

3. Третий период начался с началом 40-х годов. Военные задачи –

например, наводка зенитных орудий на быстро движущийся

самолет – потребовали недоступных человеку скоростей

вычислений и привели к разработке электронных систем.

Применение численных методов на базе ЭВМ существенно

повысило точность вычислений и расширило класс задач,

допускающих исчерпывающий анализ.

К старейшим численным методам можно отнести правила

вычисления иррациональных чисел. Рассмотрим пример, связанный с

вычислением числа .

Пример 1.1. Как известно, вычисление числа  сводится к расчету периметров

правильных многоугольников, вписанных в окружность с диаметром d=1 и

описанных вокруг нее. Пусть p– периметр вписанного правильного

многоугольника, а q– описанного вокруг окружности. Так, например, для

правильных шестиугольников p=3, q=2. Следовательно

3 <  < 2.

С ростом n периметры pрастут, а периметры qубывают, стремясь в пределе к

ВВЕДЕНИЕ В ПРЕДМЕТ «ЧИСЛЕННЫЕ МЕТОДЫ»

длине окружности:

lim;\S\do10(n((p=lim;\S\do10(n((q=  (1.1)

Таким образом, периметры

определяют число



с недостатком, а

– с

избытком:

p<  < q. (1.2)

Двухсторонняя оценка (2.2) позволяет легко контролировать точность на

каждом шаге вычисления. Погрешность вычисления е числа  можно

оценить:

е< q– p.

Приведем некоторые факты из истории вычисления числа . Великий

древнегреческий ученый Архимед (III в. до н. э.), используя формулу

удвоения, дошел до вычисления правильного 96-угольника и получил

следующую двухстороннюю оценку :

3.14084 <  < 3.14285.

К первой половине XV века в знаменитой обсерватории под

Самаркандом придворный астроном Аль-Каши вычислил  с 17 знаками

после запятой и дошел до n=62. К концу XIX века английский математик

В.Шенкс вычислил 707 знаков , затратив на это более 20 лет. В настоящее

время с помощью ЭВМ число  вычислено с фантастической точностью –

более 500 тысяч знаков.

Современные численные методы и мощные компьютеры дали

возможность решать такие задачи, о которых полвека назад могли только

мечтать. В самых разнообразных областях современной науки и техники все

чаще приходится встречаться с такими математическими задачами, для

которых невозможно получить точного решения классическими методами

или же решение может быть получено в таком сложном виде, который

совершенно неприемлем для практического использования. Так, например,

очень часто приходится встречаться с необходимостью решения систем

линейных алгебраических с десятками и сотнями неизвестных, с задачей

отыскания корней алгебраических уравнений высоких степеней и корней

трансцендентных уравнений, с необходимостью решения систем

дифференциальных уравнений, которые не интегрируются в элементарных

функциях и т.д.

Количество вычислительных задач существенно возросло в связи с

развитием науки и техники. С другой стороны, именно успехи науки и

техники дали в руки исследователей новые мощные вычислительные

средства. В свою очередь новые вычислительные средства требуют

переосмысления известных методов решения с точки зрения рациональности

их реализации на новых машинах, и вместе с тем возникает необходимость в

создании новых методов для решения все более сложных задач.

Современная вычислительная математика состоит из многих разделов,

разрабатывающих методы доведения до числового результата основных

ВВЕДЕНИЕ В ПРЕДМЕТ «ЧИСЛЕННЫЕ МЕТОДЫ»

задач математического анализа, алгебры и геометрии и пути использования

для этой цели современных вычислительных средств. Важнейшими из них

являются: вычисление значений функций, вычислительные методы линейной

алгебры, численное решение алгебраических и трансцендентных уравнений,

численное дифференцирование и интегрирование, численное решение

дифференциальных уравнений, численные методы поиска экстремумов

функций и т.д.

Итак, сегодня вычислительная математика – это научное направление,

занимающееся изучением информационных технологий автоматического

отображения (моделирования) на архитектуру вычислительных

(компьютерных) систем абстрактных вычислительных алгоритмов решения

базовых математических задач. А численные методы – раздел

вычислительной математики, объектом изучения которого являются

математические структуры, а предметом исследования – абстрактные

вычислительные алгоритмы доведения результата до числа, моделирующие

математические структуры, и способы их реализации с использованием

компьютерных инструментальных средств.

Однако численные методы не всесильны. Они не отменяют все

остальные математические методы. Начиная исследовать какое-то явление,

целесообразно использовать простейшие модели, аналитические методы и

прикидки. И только разобравшись в основных чертах явления, надо

переходить к более сложной модели и численным методам. Но даже и в этом

случае численные методы выгодно применять в комбинации с точными и

приближенными аналитическими методами. Сегодня физик, инженер,

конструктор, экономист, эколог, социолог, желающий использовать в своей

деятельности результаты математического моделирования должен одинаково

хорошо владеть классическими и численными методами математики

1.4. Контрольные вопросы и упражнения

1. Выведите рекуррентную формулу периметра p

правильного, вписанного в

окружность единичного диаметра, многоугольника с 2n сторонами. При

n=2, p

=22. Получить формулу для p

n+1

через p

2. Сделайте аналитический обзор литературы по дисциплине.

Классифицировать доступные источники по способу представления:

печатные, электронные, а также по содержанию: теоретические,

технологичные, прикладные.

3. Оцените технические характеристики своего персонального компьютера.

Проанализировать программное обеспечение личного компьютера на

предмет использования его в ходе изучения дисциплины «Численные

методы».

ВВЕДЕНИЕ В ПРЕДМЕТ «ЧИСЛЕННЫЕ МЕТОДЫ»

4. Познакомьтесь с содержанием Приложения 1. Ответьте на контрольные

вопросы и выполните упражнения.

МЕТОД ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ. СТРУКТУРА ПОГРЕШНОСТИ

Лекция 2

МЕТОД ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ. СТРУКТУРА

ПОРЕШНОСТИ

2.1. Метод вычислительной математики

Круг задач, с которыми приходится сталкиваться в вычислительной

математике, достаточно широк. Разнообразны и методы для решения этих

задач. Однако можно заметить одну общую идею этих методов. Эта идея

отчетливее всего выражается в терминах функционального анализа.

Большинство задач вычислительной математики может быть сведено

к задаче отыскания y по заданному x, записанной в следующем виде:

y=A(x) (2.1)

где xX, yY – элементы множеств соответствующих абстрактных

пространств; A – соответствие, задающее отображение XY. Основным

методом вычислительной математики является замена пространств X, Y и

функции A некоторыми другими пространствами , и функцией , более

удобными для вычислительных целей. Иногда бывает достаточно произвести

замену пространств X, Y или даже одного из них. Иногда достаточно

заменить только функцию A. Замена должна быть сделана так, чтобы

решение новой задачи

=() (2.2)

, , было в каком-то смысле близким к точному решению исходной задачи

(3) и его возможно было бы практически отыскать с сравнительно

небольшими трудностями.

Пример 2.1. Пусть необходимо вычислить интеграл

y=,

где f(x) – непрерывная функция, причем неопределенный интеграл не берется

в элементарных функциях. Чтобы получить достаточно точное

приближенное значение интеграла, можно идти двумя путями.

1. Заменим функцию f(x) алгебраическим многочленом P(x), равномерно

приближающим функцию f(x) на отрезке [a, b] с необходимой степенью

точности. В дальнейшем мы покажем, что это всегда сделать можно.

Вместо интеграла y= будем находить интеграл y=, вычисление которого не

составляет труда. Здесь мы не заменяя функционала A(x)p, заменяем

пространство, которому принадлежит f(x), пространством многочленов и

вместо функции f(x) берем многочлен P(x) из некоторой ее -окрестности.

2. Из определения интеграла следует, что всегда можно построить

интегральную сумму (;\S\do12(i=1, которая будет достаточно близка к

значению интеграла. Следовательно, вместо вычисления интеграла y=

МЕТОД ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ. СТРУКТУРА ПОГРЕШНОСТИ

можно решать другую задачу – задачу вычисления конечной суммы y=(;\

S\do12(i=1. Здесь функцию A(x)pзаменяем новой функцией A(x)(;\S\

do12(i=1.

Таким образом, перед вычислительной математикой с самой общей

точки зрения стоят следующие основные задачи:

1. Приближение множеств в функциональных пространствах.

2. Приближение функций, заданных на функциональных пространствах.

3. Разработка рациональных алгоритмов и методов решения задач в

условиях применения современных вычислительных машин.

2.2. Структура погрешности

При решении задачи y=A(x), как мы говорили выше, типична

ситуация, когда вычисление A не может быть «просто» реализовано. Чтобы

преодолеть эти сложности задачу заменяют другой =(), «близкой» к ней

задачей, которая «легко» решается численно. При этом в первую очередь

анализируют вопрос о вносимых в решение погрешностях.

Есть четыре основных источника погрешности результата

вычислений: математическая модель; исходные данные задачи;

приближенный метод и погрешность при реализации вычислений (в

частности погрешность округления):

y – погрешность математической модели, связана с допущениями при

выборе модели объекта (процесса) в силу идеализации его

действительных свойств. Уменьшать эту погрешность можно лишь

уточняя модель, что приводит к более сложной формализации.

Пример 2.2. Рассмотрим задачу об определении дальности полета l пушечного

ядра, выпущенного под углом



к горизонту со скоростью v при следующих

предположениях:

а) Земля – инерциальная система отсчета;

б) ускорение свободного падения g постоянно;

в) кривизной Земли можно пренебречь и считать ее плоской;

г) действием воздуха на движущееся ядро можно пренебречь.

Как известно из школьного курса физики при таких предположениях

(выбранной схеме идеализации процесса) задача имеет достаточно простое

решение:

l = ,

причем ядро движется по параболе.

Однако, дальнейшие исследования этой задачи показывают, что только

пренебрежение сопротивлением воздуха приводит к ошибкам в определении

дальности до 15% (при l=1 км,



=45). Более строгие математические модели