Федченко Г.М. Лекции. Численные методы
Подождите немного. Документ загружается.


РЕШЕНИЕ СЛАУ. ИТЕРАЦИОННЫЕ МЕТОДЫ
Пример 7.2. Применим метод Зейделя к системе, рассмотренной в примере
7.1.
, , тогда
Погрешность найденного третьего приближения, оцененная по норме-
максимум:
.
Остановимся подробнее на случае, когда метод Зейделя есть
модификация метода Якоби.
Представим метод Зейделя в векторно-матричном виде. Для этого
запишем неявный вид метода Якоби:
Lx
(k-1)
+Dx
(k)
+Rx
(k-1)
= b.
Равнозначный неявный вид метода Зейделя:
Lx
(k)
+Dx
(k)
+Rx
(k-1)
= b.
Тогда
x
(k)
= – (L+D)
–1
Rx
(k–1)
+ (L+D)
–1
b, k=1, 2, … .
Последнее соотношение определяет не что иное, как метод простой
итерации, где
С
= – (L+D)
–1
R, d
= (L+D)
–1
b.
Тогда можно переформулировать утверждения о сходимости метода простой
итерации применительно к методу Зейделя.
Теорема 7.6. (необходимое и достаточное условие сходимости метода
Зейделя) Метод Зейделя сходится к решению системы (7.1) в том и только
том случае, когда все корни уравнения
по модулю меньше 1.
Теорема 7.7. (достаточное условие сходимости метода Зейделя) В случае
диагонального преобладания в матрице A системы (7.1) метод Зейделя
сходится, причем быстрее, чем метод Якоби.
69

РЕШЕНИЕ СЛАУ. ИТЕРАЦИОННЫЕ МЕТОДЫ
Также для метода Зейделя справедливы оценки погрешности,
сформулированные в теореме 7.5.
Замечание 1: Вместо этих оценок, требующих дополнительных затрат на
обращение треугольной матрицы L+D допустимо использовать оценки
погрешности метода Якоби, оценивая норму матрицы C = – D
–1
(L+R), хотя
они заведомо грубее.
Замечание 2: С другими оценками погрешности приближений метода Зейделя
можно познакомиться в (Вержбицкий).
Остановимся еще на одном важном для приложений классе СЛАУ,
для которых имеет место сходимость метода Зейделя.
Определение 7.1. Система Ax = b называется нормальной, если матрица A –
симметричная положительно определенная
2
.
Теорема 7.8. Если система (7.1) – нормальная, то метод Зейделя сходится.
Любая система Ax = b может быть симметризована умножением на
матрицу A
T
. Более того справедлива следующая теорема.
Теорема 7.9. Если det A 0, то система A
T
Ax = A
T
b – нормальная.
Таким образом, если, например, известно, что система (7.1)
однозначно разрешима, но в ее матрице коэффициентов нет диагонального
преобладания, метод Зейделя можно применять к системе A
T
Ax = A
T
b. Но
здесь возникают трудности с определением критерия окончания
итерационного процесса, т.к. необходимо получить оценку погрешности
приближений. Кроме того, сходимость может оказаться медленной.
Эмпирический критерий окончания итерационного процесса
Если при решении СЛАУ итерационными методами вывести
критерий завершения итерационного процесса сложно, на практике можно
использовать следующий эмпирический критерий: если в ходе итераций
некоторая десятичная цифра повторилась в трех-четырех следующих друг за
другом итерациях, то она может считаться верной.
2
Матрица является положительно определенной, если все ее главные миноры положительны.
70

РЕШЕНИЕ СЛАУ. ИТЕРАЦИОННЫЕ МЕТОДЫ
7.6. Понятие о методе релаксации
В случаях, когда применение оценок погрешностей в методах простых
итераций и Зейделя невозможно из-за отсутствия констант, ограничивающих
сверху какие-либо нормы матрицы итерирования C соответствующего
метода, эти методы неэффективны и, более того, малонадежны ввиду
медленной сходимости. Рассмотрим обобщение метода Зейделя,
позволяющее иногда в несколько раз ускорить сходимость итерационной
последовательности.
Пусть – обозначение i-ой компоненты k-го приближения по методу
Зейделя, а – обозначение i-ой компоненты k-го приближения, получаемого
новым методом. Метод определяется равенством
, i=1,2,…,n, (7.9)
k=0,1,2…,
– задаваемые начальные значения, – параметр релаксации. Сам метод
называется методом релаксации (ослабления). Очевидно, что при =1
метод совпадает с методом Зейделя.
(7.10)
Если метод Зейделя является модификацией метода Якоби, то
расчетные формулы метода релаксации можно представить в виде:
(7.11)
Общие критерии сходимости метода релаксации выводятся
достаточно сложно. Но установлено, что для сходимости итерационного
процесса, задаваемого формулами (7.11) необходимо, чтобы (0, 2). Для
некоторых классов СЛАУ это требование к параметру релаксации является и
достаточным. Справедлива следующая теорема, обобщающая теорему 7.8.
Теорема 7.10 (Островского-Рейча). Для нормальной системы Ax = b метод
релаксации сходится при любом и любом (0, 2).
Поскольку итерационный процесс содержит параметр, естественно
подобрать его так, чтобы сходимость последовательности была наиболее
быстрой. Для отдельных важных классов задач оптимальное значение (1,
2). При (1, 2) метод называют методом последовательной верхней
релаксации (сокращенно ПВР- или SOR
3
-методом), а при (0, 1) –
методом последовательной нижней релаксации (он гораздо реже бывает
эффективным).
3
От англ. Successive Over Relaxation.
71

РЕШЕНИЕ СЛАУ. ИТЕРАЦИОННЫЕ МЕТОДЫ
7.7. Контрольные вопросы и упражнения
1. Покажите, что пределом сходящейся итерационной
последовательности, построенной с помощью рекуррентного
соотношения (7.3) является корень уравнения (7.2).
2. Докажите достаточное и необходимое и достаточное условия
сходимости метода Якоби как следствия теорем 7.1 и 7.2.
3. Получите соотношение (7.8) для оценки погрешности k-ого
приближения метода простой итерации.
4. Докажите достаточное условие сходимости метода Зейделя как
следствие теоремы 7.3.
5. (*) Докажите необходимое и достаточное условие сходимости
метода Зейделя как следствие теоремы 7.4.
6. Для системы
с симметричной положительно определенной матрицей и очевидным
решением выполнить по три итерационных шага, начиная с методами
Якоби, Зейделя и ПВР с параметром релаксации =1.1. Сравнить
погрешности приближений, полученных на третьем шаге каждым
методом, по норме-максимум.
72

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Лекция 8
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
8.1. Постановка задачи
В данной лекции рассмотрим способы решения нелинейных уравнений
с одним неизвестным. Каждое такое уравнение можно представить в виде:
f(x) = 0. (8.1)
Область определения D
f
функции f также называют областью определения
уравнения.
Определение 8.1. Число t называется корнем уравнения (8.1) или нулем
функции f, если при подстановке его вместо x уравнение превращается в
верное равенство
Определение 8.2. Число t называется корнем k-й кратности, если при x=t
вместе с функцией f(x) обращаются в ноль все ее производные до (k-1)
порядка включительно:
0
1
tf...tftftf
k
.
Однократный корень называется простым.
Корни уравнения могут быть действительными и комплексными. В
дальнейшем будем говорить только о вычислении действительных корней.
Решить уравнение – это значит найти множество всех его корней. Два
уравнения называются эквивалентными, или равносильными, если у них
одинаковое множество корней.
Различные разделы математики рассматривают классы уравнений,
которые можно решить точно с помощью аналитических преобразований. Но
точные методы не являются основными в практике вычислений по
нескольким причинам:
Существуют уравнения, которые вообще не могут быть решены точно. В
первую очередь это относится к большинству трансцендентных
уравнений, например: sin x – e
x
= 0. Для алгебраических уравнений еще в
начале XIXв. Абелем и Галуа доказано, что нельзя построить формулу,
73

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
по которой можно было бы решать произвольное уравнение P
n
(x)=0
степени выше четвертой.
Многие точные методы настолько трудоемки, что применять их
нецелесообразно.
Часто точное решение не является необходимым. Задачу отыскания
корней можно считать практически решенной, если найдены их
приближения с заданной степенью точности.
Несмотря на появление математических пакетов, способных выполнять
на компьютере символьные преобразования, большинство
компьютерных инструментальных средств позволяют легко реализовать
именно вычислительные алгоритмы.
При решении любого уравнения необходимо:
1. установить, имеет ли оно действительные корни и их количество;
2. вычислить корни точно, если это возможно и имеет смысл, или
приближенно с заданной степенью точности.
Определение 8.3. Поиск приближенного значения корня с точностью до
заданного достаточно малого числа > 0 называется уточнением корня.
Задача уточнения будет решена, если найдется число x
*
такое, что
*
xt
.
Тогда t x
*
с точностью до .
Если будет найден такой отрезок [a; b], что корень уравнения t[a; b]
и b–a
, то любое число x
*
из этого отрезка можно взять в качестве
приближенного значения корня с точностью до . А значение
t
ba
x
2
*
с
точностью
2
.
Упражнение. Докажите, что значение
2
*
ba
x
является приближенным значением
к корню t с точностью
2
, если t[a; b] и b–a.
8.2. Геометрическая интерпретация
Пусть дано уравнение f(x) = 0. Построим график функции y=f(x).
74
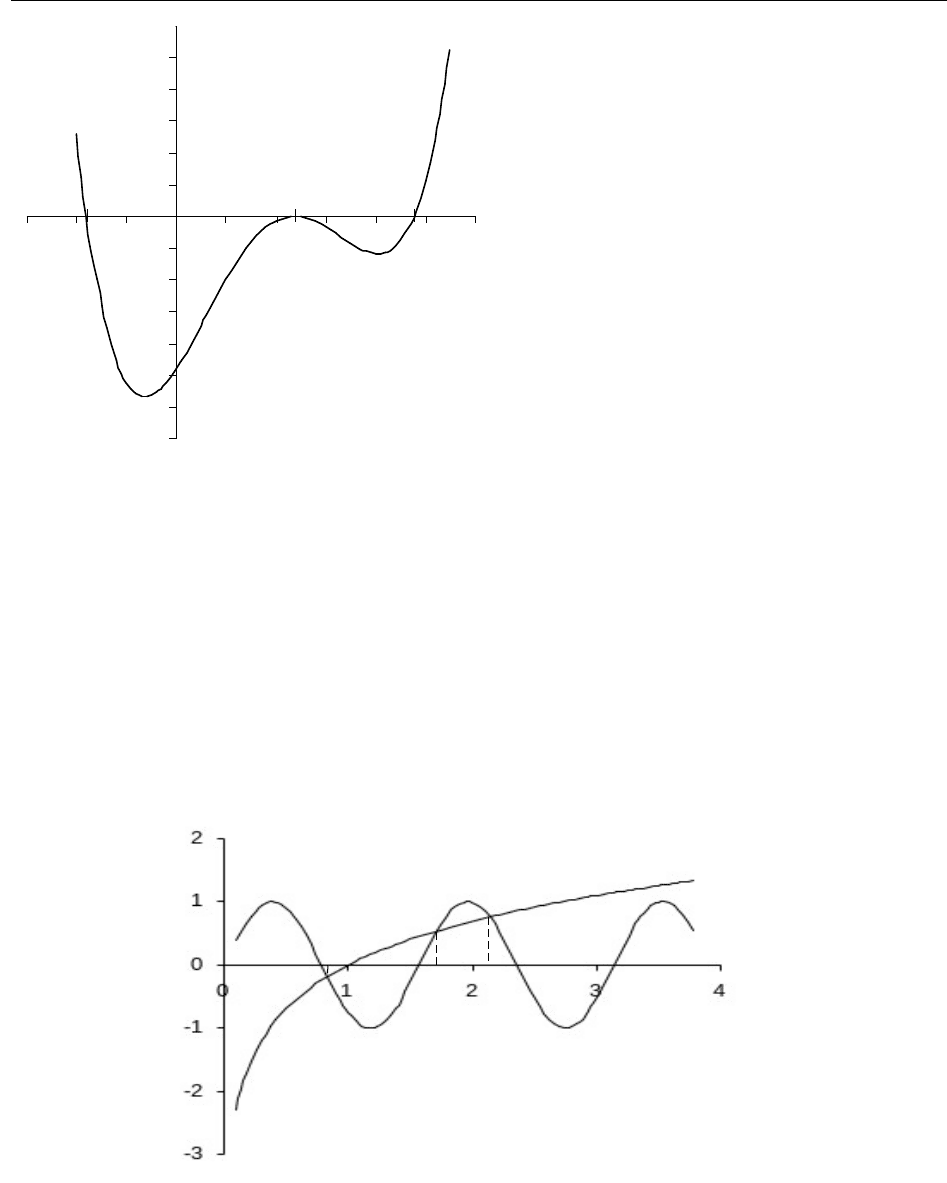
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Абсциссы точек пересечения
графика с осью Ox и являются
корнями уравнения. На этом
построен графический метод
решения уравнений. Этот метод
нагляден и прост, но позволяет
получить лишь грубые
приближения значения корней
уравнения. Вместе с тем этой
точности часто бывает достаточно
для решения многих практических
задач.
Иногда удобнее записать исходное уравнение в эквивалентном виде
(x)=g(x), в случае если функции y=
(x), y=g(x) имеют несложные графики.
Абсциссы точек пересечения этих графиков и будут корнями исходного
уравнения. Например, уравнение sin 4x – ln x = 0 удобно преобразовать к
виду sin 4x = ln x. Для нахождения корней уравнения достаточно найти
абсциссы точек пересечения графиков функций y=sin 4x и y=ln x:
Рис. 8.2. Графики функций y=sin 4x и y=ln x
Построив графики функций на промежутке [0; 4] и принимая во
внимание свойства функций y=sin 4x и y=ln x, можно констатировать, что вне
данного промежутка уравнение sin 4x – ln x = 0 корней не имеет. Уравнение
имеет три действительных корня: t
1
0,8, t
1
1,7 и t
1
2,1.
75
x
y
t
1
t
2
t
3
y = sin 4x
y = ln x
-3 -2 -1 0 1 2 3 4 5 6
x
y
t
1
t
2
t
3
y = f(x)
Рис. 6.1. График функции y=f(x)

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Для получения корней с большей точностью применяются численные
методы, о которых и пойдет речь в данной теме. Процесс нахождения
приближенных корней уравнения разбивается на два этапа:
1. отделение корней,
2. уточнение корней до заданной степени точности.
8.3. Отделение корней
Определение 8.4. Корень t отделен на отрезке [a; b]pD
f
, если t (a; b) и
других корней в этом отрезке нет. Отрезок [a; b] называется отрезком
изоляции корня t.
Отделить корни уравнения f(x) = 0 – значит для каждого из корней
найти свои отрезки изоляции.
Отделение корней обычно начинают проводить графически. Для этого
строят графики функций, получают интервалы, в которых находятся корни
уравнения. Это предположение затем проверяют аналитически, пользуясь
свойствами непрерывных и дифференцируемых функций, которые изучаются
в курсе математического анализа.
Теорема 8.1 (теорема о существовании корня). Если функция f(x)
определена и непрерывна на отрезке [a; b], причем на концах его принимает
значения разных знаков, т.е. f(a) f(b)<0, то существует по крайней мере одна
точка t1(a; b), в которой значение функции равно нулю.
Теорема 8.2 (теорема о единственности корня). Если функция f(x)
определена, непрерывна, монотонна на отрезке [a; b] и принимает на концах
отрезка значения разных знаков, то существует единственная точка t (a; b),
в которой значение функции равно нулю.
Таким образом, корень t заведомо будет единственным, если
производная f
(x) существует и сохраняет постоянный знак внутри интервала
(a; b), т.е. если f
(x)>0 (или f
(x)<0) при a<x<b.
Пример 8.1. Отделить корни уравнения x
5
–
4x
2
+ x
= 0.
Функция f(x)= x
5
–
4x
2
+ x определена и непрерывна на всей действительной
оси, а также
.)(lim,)(lim
xfxf
xx
Следовательно уравнение
имеет по крайней мере один корень.
76
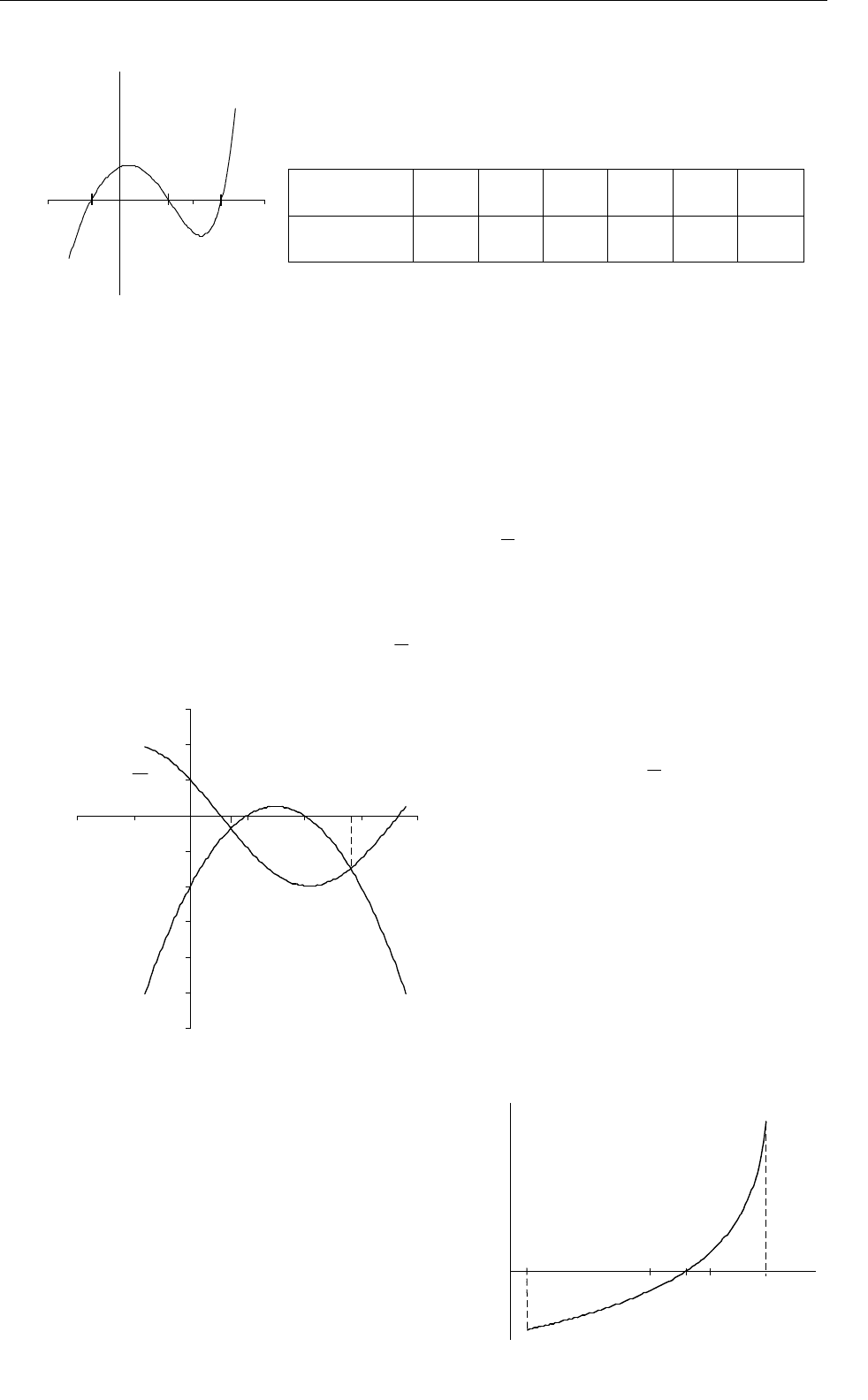
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Составим таблицу знаков функции f(x):
x – –1 0 1 2 +
sign f(x) – – + – + +
Рис. 8.3. График функции y=x
5
– 4x
2
+x
Уравнение x
5
–
4x
2
+ x
= 0 имеет три действительных корня:
t
1
[-1; 0], t
2
[0; 1], t
3
[1; 2].
Пример 8.2. Отделить корни уравнения
023
3
cos2
2
xxx
.
Уравнение удобно представить в виде:
23
3
cos2
2
xxx
и построить графики функций
3
cos2 xx
и
23
2
xxxg
.
Уравнение имеет два корня:
t
1
[0,5; 1], t
2
[2,5; 3].
Рис. 8.4. Графики функций
(x) и g(x)
8.4. Метод половинного деления
Пусть дано уравнение f(x)=0. Будем считать, что отделение корней
произведено и на отрезке [a; b] расположен один корень t. Требуется найти
77
-6
-5
-4
-3
-2
-1
0
1
2
3
-2 -1 0 1 2 3 4
3
cos2
xx
23
2
xxxg
t
1
t
2
x
y
y=f(x)
a
b
c
1
b
1
a
1
c t
Рис. 6.5. Геометрическая
интерпретация метода половинного
деления
-1 0 1 2

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
приближенное значение корня с точностью до
, где
– достаточно малое
положительное число.
Итак, функция f непрерывна на [a; b] и f(a)
f(b)<0. Разделим [a; b] пополам точкой
2
ba
c
и вычислим f(c). Проверим
следующие условия:
1. Если f(c)=0, то c – корень. t=c.
2. Если f(a) f(c)<0, то корень лежит в
интервале [a; c].
3. Если f(c) f(b)<0, то корень лежит в
интервале [b; c].
Выберем ту половину отрезка, на концах которой функция принимает
значения разных знаков, и обозначим ее [a
1
; b
1
]. Затем отрезок [a
1
; b
1
]
делим пополам точкой
2
11
1
ba
c
и проводим аналогичные рассуждения.
Получится либо точный корень t=c
1
, либо отрезок [a
2
; b
2
] со свойством
f(a
2
)pf(b
2
)<0. И так далее.
Если на каком-то шаге обнаружится точный корень (что практически
маловероятно), то процесс деления пополам закончится нахождением
точного значения. Если нет, то получится бесконечная последовательность
вложенных отрезков [a; b]=[a
0
; b
0
][a
1
; b
1
][a
2
; b
2
]…[a
n
; b
n
]…, где
,...2,1при
2
,
0если,;
0если,;
;
11
1
1111
1111
n
ba
с
bfcfbc
cfafca
ba
nn
n
nnnn
nnnn
nn
(8.2)
Длина отрезков
0
2
n
nn
ab
ab
при n. Следовательно, полученная
последовательность отрезков является стягивающейся. В силу
непрерывности f на [a; b] и теоремы Кантора о стягивающейся
последовательности вложенных отрезков
tc
n
n
lim
.
Упражнение. Докажите, что
tc
n
n
lim
.
Для того, чтобы найти приближенное значение корня с точностью до >0,
необходимо остановить итерационный
4)
процесс половинного деления на
таком шаге n, где b
n
– a
n
2. Тогда
за приближенное значение корня
можно взять величину
2
*
nn
ba
x
.
*
xt
с точностью
, так как
*
xt
(рис. 3.8).
4)
Итерация (от лат. iteratio – повторение) – неоднократное применение какой-нибудь операции.
78
x
a
n
b
n
x
*
t
2
Рис. 6.6.
