Федченко Г.М. Лекции. Численные методы
Подождите немного. Документ загружается.


ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Количество итераций n, необходимых для достижения заданной точности
,
можно определить по формуле:
)2
2
log
ab
n
.
(8.3)
Упражнение. Докажите, что
ab
n
2
log
.
Замечания:
1. Метод половинного деления дает простой и удобный алгоритм уточнения
корней с любой наперед заданной степенью точности. Он требует от
функции f легко проверяемых свойств: непрерывности на отрезке
изоляции корня и разных знаков значений на его концах. Это
обеспечивает его применимость к обширному классу уравнений.
2. Скорость приближения к корню зависит лишь от длины начального
отрезка [a; b] и заданной точности
и не зависит от функции f.
3. На каждом шаге итерации погрешность приближенного значения корня
уменьшается ровно вдвое (и только). Вследствие этого увеличение
точности всегда сопровождается пропорциональным ростом объема
вычислений.
4. Если на отрезке, на концах которого непрерывная функция f принимает
значения разных знаков, содержится несколько корней, то процесс
половинного деления сойдется к одному из них (к какому заранее
неизвестно).
Упражнение. Легко убедиться, что уравнение x
3
–7x
2
+14x–8=0 имеет три корня 1, 2,
4. К какому корню сойдется процесс половинного деления, если
выбрать в качестве начального отрезок [0; 5]?
5. Метод неприменим к корням четной кратности.
6. Для корней нечетной высокой кратности метод слабо устойчив к ошибкам
округления, возникающим при вычислении f(x).
7. Метод половинного деления не обобщается на системы уравнений.
Упражнение. Вычислите положительный корень уравнения x
2
–2=0 методом
половинного деления с точность до 0,1. Какое количество шагов для
этого потребовалось, если длина начального отрезка локализации
корня равна 1?
.2)
[x] – целая часть x, т.е. наибольшее целое, не превышающее x.
79

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
8.5. Метод простой итерации
Пусть корень t уравнения f(x)=0 отделен на отрезке [a; b]. Путем
эквивалентных преобразований перейдем к уравнению вида:
x =
1(x), (8.4)
где
1(x) непрерывна на [a; b].
Выбрав в качестве начального приближения произвольное x
0
[a; b],
построим итерационную последовательность
x
1
=
1(x
0
), x
2
=
1(x
1
), …, x
n
=
1(x
n-1
), … (8.5)
Если полученная таким образом последовательность1(x
n
) сходится, то
сходится она к корню уравнения (8.4), а значит и уравнения (8.1), т.е.
tx
n
n
lim
.
Пусть
zx
n
n
lim
. В силу непрерывности функции
)()lim()(limlim
11
zxxxz
n
n
n
n
n
n
Поскольку корень уравнения (5.1) на отрезке [a; b] единственный t = z.
Об условии сходимости итерационной последовательности говорит
последующая теорема.
Теорема 8.3 (достаточное условие сходимости итерационной
последовательности). Если
1. функция
1(x) определена и дифференцируема на отрезке [a; b];
2.
1(x) [a; b] для всех x [a; b];
3. существует такое положительное число q1<p1, что |p
(x)p|ppq для всех
x1p[a;pb],
то итерационная последовательность x
n+1
=
1(x
n
) (n=0,1,2,…) с любым
начальным приближением x
0
p[a;pb] сходится к корню уравнения x =
1(x).
Этот корень – единственный на [a;pb].
Отметим, что в силу условия 2 все члены итерационной
последовательности x
n
p[a;pb].
Рассмотрим два последовательных приближения
).(),(
11
nnnn
xxxx
80

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Отсюда
).()(
11
nnnn
xxxx
По теореме Лагранжа
что],;[
1 nn
xxc
))(()()(
11
nnnn
xxcxx
. Таким
образом
))((
11
nnnn
xxcxx
.
Переходя к модулю и принимая во внимание условие 3 теоремы, получим:
11
nnnn
xxqxx
.
При n=1,2,… будем иметь:
011
01
2
1223
0112
xxqxx
xxqxxqxx
xxqxx
n
nn
(8.6)
Рассмотрим ряд
...)(...)()(
112010
nn
xxxxxxx
(8.7)
Составив частичные суммы этого ряда S
1
=x
0
, S
2
=x
1
, S
3
=x
2
, …, S
n+1
=x
n
, …,
заметим что последовательность частичных сумм ряда (8.7) совпадает с
итерационной последовательностью.
Сравним отрезок ряда (8.7), начиная со второго слагаемого, с рядом
......
01
1
01
2
0101
xxqxxqxxqxx
n
(8.8)
Абсолютные величины членов ряда (8.7) не превосходят соответствующих
членов ряда (8.8). Ряд (8.8) сходится как бесконечно убывающая
геометрическая прогрессия (q<1). Следовательно, сходится, причем
абсолютно, ряд (5.4), сходится и последовательность его частичных сумм.
Следовательно, построенная итерационная последовательность (x
n
)
сходящаяся. Как было доказано выше, сходится она к корню уравнения x =
1(x):
tx
n
n
lim
.
Единственность корня докажем методом от противного. Пусть
t
– еще один
корень уравнения на отрезке [a;pb]:
)(tt
. Тогда
)()( tttt
,
и, следовательно, в соответствии с теоремой Лагранжа
что],;[ ttc
))(( ttсtt
,
0))(1)((
сtt
.
В силу условия 3 теоремы
0)(1
с
. Следовательно,
0 tt
и корень t единственный.
Упражнение. Покажите, что при выполнении условий теоремы 8.3 выполняются
неравенства
,...)2,1(,
0
nxtqxt
n
n
.
81

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Замечания:
1. Условия теоремы 8.3 являются достаточными, но не необходимыми.
2. Чем меньше число q, тем быстрее сходится итерационная
последовательность.
3. Метод простой итерации является самоисправляющимся. Если какое-то
приближение x
n
найдено с ошибкой, не выводящей его за пределы отрезка
[a; b], то последующие члены все равно будут приближаться к корню, так
как ошибочное значение можно рассматривать как новое начальное
приближение x
0
.
Теорема 8.4. Если на отрезке [a; b] функция
1(x) определена и
дифференцируема, причем
|p
(x)p|pp1при всех x [a; b],
то итерационная последовательность x
n+1
=
1(x
n
) (n=0,1,2,…) не сходится к
корню t1p[a;pb] ни при каком x
0
t из этого отрезка.
Обозначим
0
0
xtr
. Применяя теорему Лагранжа можно показать, что
для всех x
n
[a; b]
rxt
0
. Следовательно, последовательность1(x
n
) не
сходится к t1p[a;pb].
Для геометрической интерпретации метода простой итерации выберем
возрастающую функцию y=
(x). В случае 1)
возрастает на [a; b]
медленнее, чем функция y=x, т.е. 0pp
(x)p<p1. В случае 2)
возрастает на
[a; b] быстрее, чем функция y=x, т.е.
(x)p>p1.
1) 2)
Рис. 8.7. Геометрическая интерпретация метода простой итерации
1) 0OO
O<O1, 2)
O>O1.
82
a
b
x
1
x
2
x
0
t
0
A
0
y
x
B
1
B
2
A
1
A
2
y=x
y=
(x)
a
b
x
1
x
0
t
0
A
0
y
x
B
1
B
2
A
1
y=x
y=
(x)
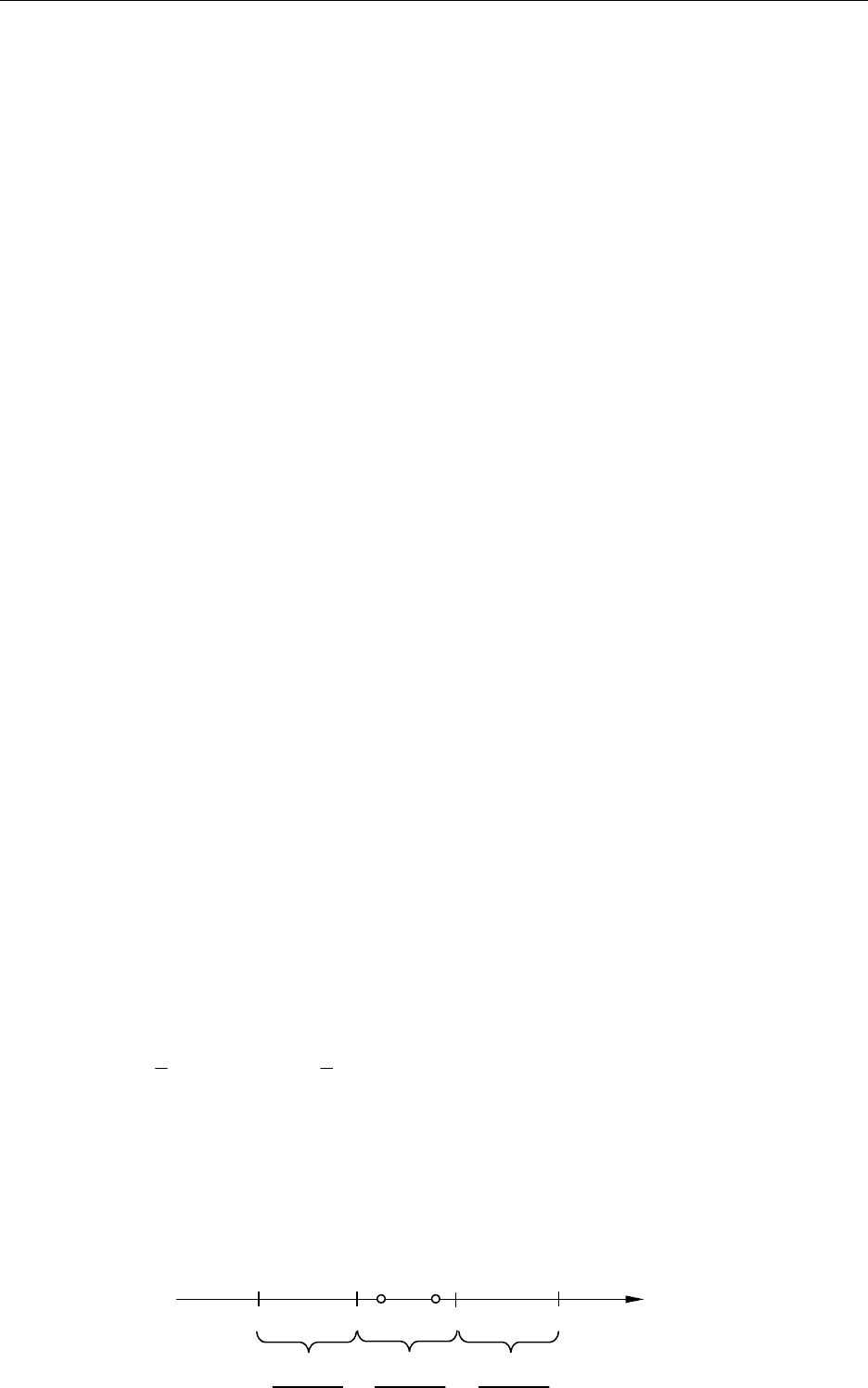
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Построим графики функций y=x и y=
(x). Корнем уравнения x=
(x)
является абсцисса t точки пресечения этих графиков. Взяв в качестве
начального приближения некоторое x
0
, вычислим
(x
0
) и получим на
графике функции
точку A
0
(x
0
,
(x
0
)). Линия проекции этой точки на ось Oy
пересечет прямую y=x в точке B
1
. Проекция B
1
на ось Ox и дает x
1
(x
1
=
(x
0
)).
Вычислив
(x
1
) и спроецировав точку A
1
(x
1
,
(x
1
)) графика функции
на ось
Oy, найдем точку B
2
на прямой y=x и ее проекцию x
2
на ось Ox (x
2
=
(x
1
)) и
так далее. Таким образом на рисунке мы видим ломанную A
0
B
1
A
1
B
2
A
2
… в
виде «лестницы», которая в случае |p
(x)p|p< 1 стремится к точке пересечения
графиков, а в случае |p
(x)p|p> 1 удаляется от нее.
Упражнение. Постройте геометрическую интерпретацию итерационной
последовательности для убывающей функции y=
(x). При этом
рассмотрите случаи когда
1)
убывает медленнее, чем функция y=–x, т.е. –1p<p
(x) p0,
2)
убывает быстрее, чем функция y=–x, т.е.
(x)p<p–1.
Упражнение. Покажите геометрически, что возможны ситуации, когда в
окрестности корня для
не выполняются ни условия теоремы 8.3, ни
теоремы 8.4, и что в этом случае сходимость или расходимость
итерационной последовательности может зависеть от выбора x
0
.
Упражнение. Проиллюстрируйте геометрически, что при невыполнении условия 2)
теоремы 8.3 можно получить расходящуюся итерационную
последовательность.
Если проверка того факта, что для всех x [a; b] значения функции
1(x) [a; b] затруднительно, то прибегают к правилу утроенного отрезка,
опирающегося на нижеследующую теорему.
Теорема 8.5 (второе достаточное условие сходимости итерационной
последовательности). Если
1. функция
1(x) определена и дифференцируема на отрезке [a; b];
2. корень уравнения x=
1(x) содержится в средней трети отрезка: tp [
;
],
где
)(
3
1
aba
,
)(
3
1
abb
;
3. существует такое положительное число q<1, что |
(x)|q для всех
x1p[a;pb],
то итерационная последовательность x
n+1
=
1(x
n
) (n=0,1,2,…) с любым
начальным приближением x
0
p[
;
] сходится к корню уравнения x =
1(x).
Этот корень – единственный на [a;pb].
83
x
b
x
0
t
3
ab
a
3
ab
3
ab

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Рис. 8.8. Правило утроенного отрезка
Пример 8.3.
Рассмотрим уравнение x
3
–3x+1=0.
Построив график функции y=x
3
–3x+1,
определим, что уравнение имеет три корня.
К виду x =
1(x) это уравнение можно привести
несколькими способами. Например:
а)
3
1
3
x
x
;
б)
12
3
xxx
;
в)
3
13 xx
.
Проверим, какое из приведенных представлений позволяет уточнить
методом простой итерации корень t
2
[0; 1]. Для этого рассмотрим более
узкий отрезок изоляции корня [0,2; 0,4]. Тогда по правилу утроенного
отрезка необходимо оценить сверху |
(x)| на отрезке [0; 0,6].
В случае а) |
(x)|=x
2
– возрастает на исследуемом отрезке, следовательно
принимает наибольшее значение в правом конце, поэтому |
(x)|pp0,36p<p1.
На основании теоремы 8.5 итерационная последовательность, полученная по
формуле
3
1
3
1
n
n
x
x
, n=0,1,2,…, сходится к корню t
2
при любом начальном
приближении x
0
[0; 0,6]. Например, при x
0
=0,2 получим три первых члена
итерационной последовательности:
336,0
3
12,0
3
1
x
346,0
3
1336,0
3
2
x
347,0
3
1346,0
3
3
x
С помощью рисунка 8.10 можно
проиллюстрировать графически
сходящуюся последовательность,
84
-2
-1
0
1
2
3
4
-2 -1 0 1 2
Рис. 6.9. График функции
y=x
3
–3x+1
t
1
t
2
t
3
0
0,2
0,4
0,6
0,8
1
0 0,2 0,4 0,6 0,8 1
y
x
y=x
3
1
3
x
y
t
x
0
Рис. 6.10. Графики функций
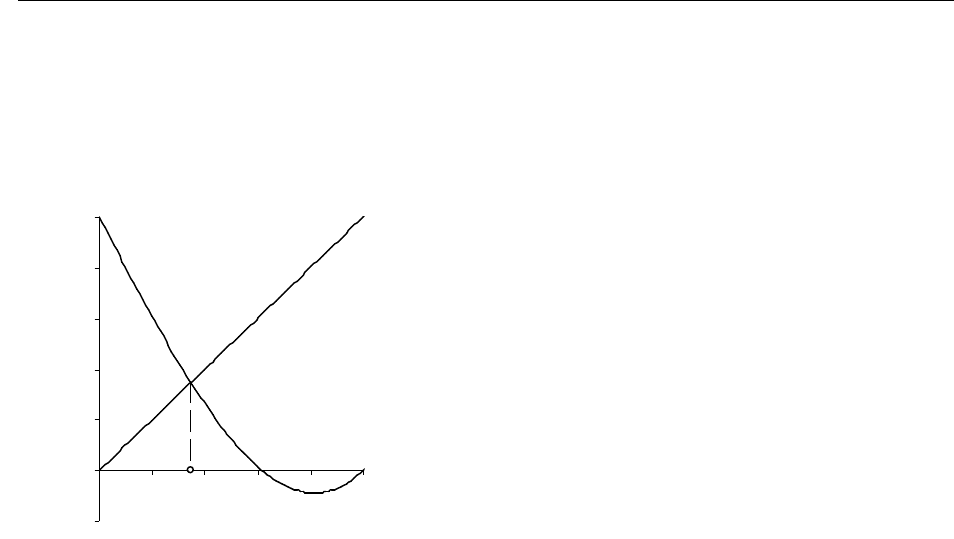
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
построенную по методу простой
итерации для данного случая.
В случае б) |
(x)|=|3x
2
–2|=2–3x
2
на отрезке
[0,2; 0,4], принимает значения от 1,96
уменьшаясь до 1,84 (т.е.>1). Следовательно,
в силу теоремы 8.4 независимо от выбора
начального приближения x
0
[0,2; 0,4]
итерационная последовательность
расходится. С помощью рисунка 8.11 можно
проиллюстрировать графически
расходящуюся последовательность,
построенную по методу простой итерации
для данного случая.
Случай в) рассмотрите самостоятельно.
8.6. Приведение уравнения к виду, удобному для применения
метода простой итерации
Уравнение f(x)=0 можно записать в виде (8.4): x =
1(x) различными
способами. Причем способ записи отнюдь не безразличен, так как в одних
случаях |
(x)| окажется малым в окрестности корня t, в других – большим.
Кроме того, пригодное для уточнения одного корня представление x =
1(x)
может оказаться непригодным для другого корня этого же уравнения, и
наоборот. Для применения метода простой итерации выгодно такое
представление x1=p
1(x), при котором выполнено неравенство
|
(x)|ppq1<p1, (8.7)
причем, чем меньше число q, тем быстрее сходится итерационная
последовательность к корню
Рассмотрим некоторые общие приемы преобразования уравнения
f(x)=0 к виду (8.4).
Способ 1. Обе части уравнения f(x)=0 умножим на число –k, затем прибавим к
обеим частям x. Получим уравнение, равносильное исходному:
x = x – k1f(x). (8.8)
85
Рис. 6.11. Графики функций
y=x и y=x
3
–2x+1
-0,2
0
0,2
0,4
0,6
0,8
1
0 0,2 0,4 0,6 0,8 1
y
x
y=x
y=x
3
–2x+1
t

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Таким образом,
1(x) = x – k1f(x). Подберем k так, чтобы имело место
условие (8.7). В случае, если корень t локализован на средней трети отрезка
[a; b] и для всех x1p[a;pb]
0 < m f
(x) M,
то можно выбрать
M
k
1
. В этом случае
(x) = 1 – k1f
(x) удовлетворяет
неравенству
1– k M
(x) 1– k1m,
или
M
m
x
1)(0
.
Тогда в качестве q можно выбрать число
110
M
m
q
такое, что при всех x1p[a;pb]
qx
)(0
.
Способ 2. Если f(x) содержит в себе выражение некоторой обратимой на
отрезке [a;pb] функции y =
(x) такой, что |
(x)|p k1>p1 для всех x1p[a;pb],
то следует попытаться заменить уравнение f(x)=0 на равносильное вида (8.4)
с использованием функции x=
1(y), обратной к
. В силу соотношения
между производными для взаимообратных функций
(y)=1/
(x)
1
1
|)(|
1
|)(|
kx
y
.
Способ 3. Если корень t уравнения f(x)=0 локализован на средней трети
отрезка [a; b], функция f дифференцируема на p[a;pb] и для всех x1p[a;pb]
0 < m f
(x) M,
то приведение к виду
)(
2
xf
mM
xx
удовлетворяет всем свойствам теоремы 8.5, а значит соответствующая
итерационная последовательность сходится к t с любым начальным
приближением x
0
p[
)(
3
1
aba
;
)(
3
1
abb
].
Пример 8.4. Рассмотрим уравнение x
3
–3x+1=0. Корень t
3
уравнения можно
локализовать на отрезке [1,4; 1,6] (см. пример 8.3, рис. 8.9). В соответствии с
правилом утроенного отрезка уравнение необходимо привести к виду
x1=p
1(x) так, чтобы |
(x)|ppq1<p1 при всех x1p[1,2;p1,8].
Способ 1. На отрезке [1,2;p1,8] f
(x)=3x
2
–3>0 и возрастает. Следовательно,
f
(1,2)ppf
(x)pp f
(1,8). Поэтому m1= f
(1,2) = 1,32; M = f
(1,8) = 6,72, а значит
kp=p0,15; qp=p0,81. Таким образом, для уточнения корня t
3
методом простой
итерации можно использовать уравнение
86
1
1,2
1,4
1,6
1,8
2
1 1,2 1,4 1,6 1,8 2
y
x
y=x
3
13 xy
t
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
15,045,115,0)13(15,0
33
xxxxxxx
с любым начальным приближением x
0
[1,4; 1,6].
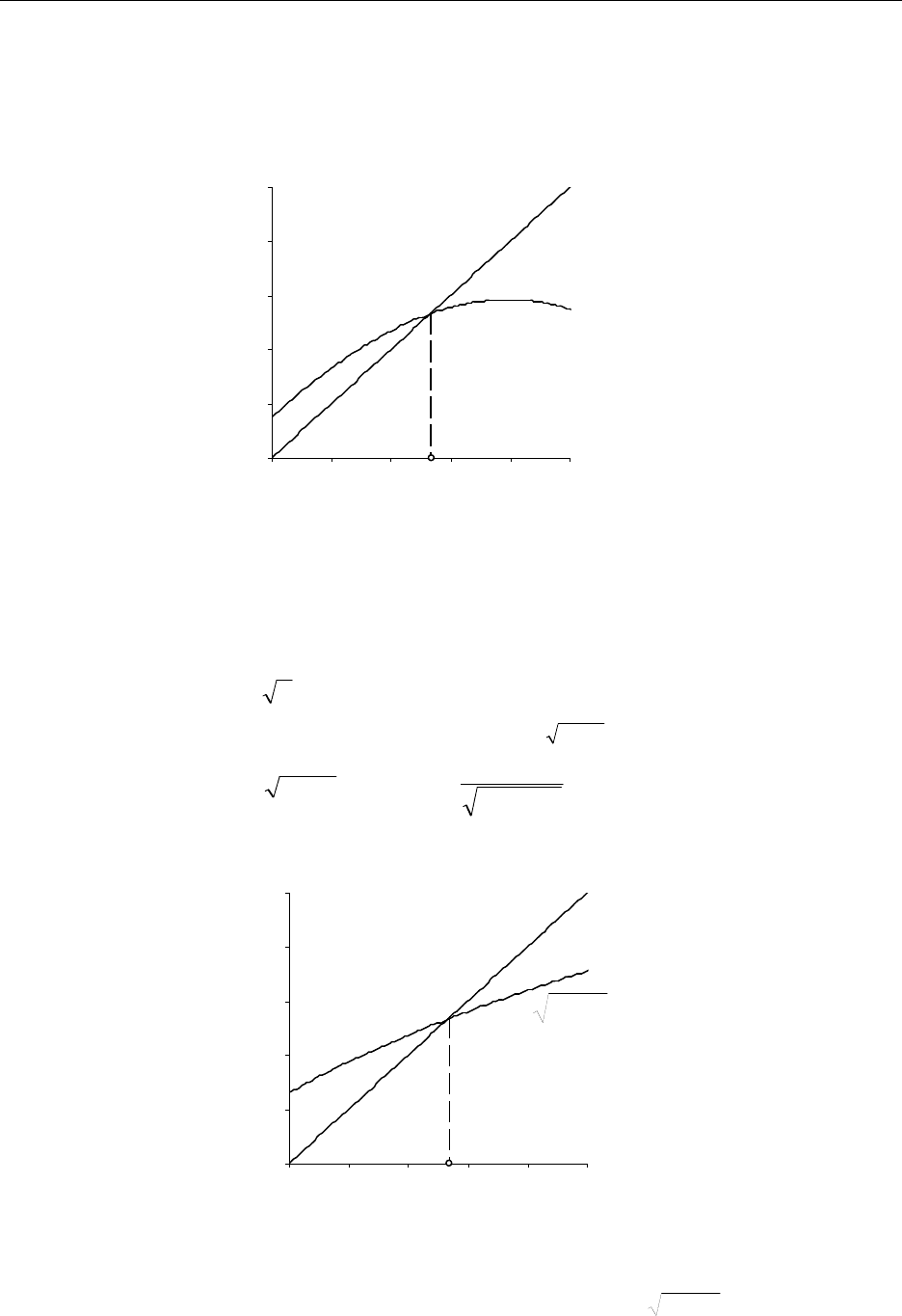
Рис. 8.12. Графики функций y=x и y=–0,15x
3
+1,45x–0,15
Способ 2. Уравнение x
3
–3x+1=0 можно представить в равносильном виде
x
3
=3x–1. На отрезке [1,2;p1,8]
(x)=( x
3
)=3x
2
>1. Перейдем от функции y=x
3
к
обратной функции
3
yx
:
3
3
1313 xxxx
.
В этом случае
3
13)( xx
и
3
2
)13(
1
)(
x
x
. На отрезке [1,2;p1,8]
(x)
положительна и убывает, и потому |
(x)| p
(1,2) 0,53<1.
Рис. 8.13. Графики функций y=x и
3
13 xy
87
1
1,2
1,4
1,6
1,8
2
1 1,2 1,4 1,6 1,8 2
y
x
y=x
y=–0,15x
3
+1,45x–0,15
t

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
8.7. Оценка погрешности приближений
При выполнении условий теорем 8.3 или 8.5 для оценки погрешности
приближений к корню t, полученных с помощью метода простой итерации
справедлива формула
||
1
||
1
nnn
xx
q
q
xt
.
Итак, уравнение приведено к виду x1=p
(x). Обозначим f(x)p=px1–p
(x).
Очевидно, что f(x) дифференцируема на заданном отрезке и f(t)=0.
qxxxf
1|)(|1|)(1||)(|
.
Оценим
nn
xx
1
:
|,|)1(|||)(|/Лагранжат.по/
|)()(||)(||)(|
1
nn
nnnnnn
xtqxtcf
xftfxfxxxx
где c1p[t;px
n
]. Таким образом,
nnn
xx
q
xt
1
1
1
||
,
а
11
nnnn
xxqxx
(см. доказательство т. 8.3).
Получаем
||
1
||
1
nnn
xx
q
q
xt
Таким образом, если задана точность >0 для вычисления приближенного
значения корня, то итерационный процесс необходимо закончить при
выполнении условия
||
1
1nn
xx
q
q
и за приближенное значение корня взять tx
n
.
Для каждого шага метода простой итерации можно определить абсолютную
погрешность приближения x
n
:
||
1
1
nn
xx
q
q
n
x
.
Замечания:
Если
2
1
q
, то
1
||
nnn
xxxt
,
а условием окончания итерационного процесса при заданной точности
>0 будет выполнение неравенства
1nn
xx
.
Если –1p<p–q1p
(x)p<p0 (функция
убывает) на выбранном отрезке, то
приближения x
n-1
, x
n
находятся по разные стороны t, т.е. на каждом шаге
итерации t1p[px
n-1
, x
n
]. И в этом случае оценка приближений имеет вид
1
||
nnn
xxxt
.
Для оценки погрешности приближений в методе простой итерации можно
пользоваться формулой
...,2,1nпри
1
||
01
xx
q
q
xt
n
n
88
