Федченко Г.М. Лекции. Численные методы
Подождите немного. Документ загружается.


РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Выбрав в качестве начального приближения x
0
=1, y
0
=2, получим:
Учитывая, что решение системы x
*
≈0.546299178, y
*
≈1.72685411, оценим
абсолютную погрешность третьего приближения
.
Проверьте, что погрешности третьих приближений, полученных методом
простой итерации и методом Зейделя для решения данной системы (примеры
12.1, 12.2) больше, чем данная погрешность. Действительно, в соответствии с
теоретическими и достаточно сложными рассуждениями, метод Ньютона
имеет более быструю, квадратичную скорость сходимости (при условии, что
сходимость вообще наблюдается).
Эмпирический критерий окончания итерационного процесса
Так как при решении системы нелинейных уравнений итерационными
методами вывести критерий завершения итерационного процесса сложно, на
практике можно использовать следующий эмпирический критерий: если в
ходе итераций некоторая десятичная цифра повторилась в трех-четырех
следующих друг за другом итерациях, то она может с большой степенью
достоверности считаться верной.
10.5. Контрольные вопросы и упражнения
1. На основе представления 10.9 системы уравнений из примера 10.1
запишите рекуррентные формулы для вычисления итерационной
последовательности и найдите три приближения, выбрав в качестве
начального приближения x
0
=1, y
0
=1. Получилась ли сходящая
последовательность?
2. Постройте геометрическую интерпретацию метода Зейделя для
системы из примера 10.2.
3. Оцените абсолютные погрешности приближений, полученных в
примерах 10.1, 10.2. Также оцените max;\s\do9(i=1…n для каждых пар
приближений и сравните их с соответствующими погрешностями.
4. (*) Основные вычислительные затраты в методе Ньютона приходятся
на вычисление и обращение матрицы Якоби. Возможна следующая
модификация метода Ньютона: матрица Якоби вычисляется и
обращается лишь один раз – в начальной точке и этот множитель
участвует во всех шагах итерации:
, k=0, 1, 2, … (10.16)
Таким образом, расчетные формулы для случая двух уравнений с двумя
неизвестными примут вид:
109

РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
, k=0, 1, 2, … (10.17)
Этот метод требует значительно меньших вычислительных затрат на
один итерационный шаг, но итераций при этом может потребоваться
больше по сравнению с обычным методом Ньютона. Вычислите три
приближения решения системы примера 10.3 модифицированным
методом Ньютона и оцените погрешности этих приближений. Сравните с
методом Ньютона.
110

ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
Лекция 11
ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
11.1. Постановка задачи аппроксимации функций
В основе многих численных методов лежит замена одной функции
f(x) другой функцией (x), близкой к f(x) и обладающей «хорошими»
свойствами, позволяющими легко производить над нею аналитические или
вычислительные операции. Такая замена называется аппроксимацией или
приближением функции f(x) функцией (x).
Поводом для аппроксимации функции может послужить, в частности,
табличный способ ее задания. Такое задание функции встречается, например,
когда значения функции, представляющей собой некоторую физическую
величину, получаются из опыта (в дискретные моменты времени снимаются
показания приборов), а аналитическое выражение функции неизвестно.
Предположим, что в результате некоторого эксперимента для
конечного набора значений х
i
величины х из отрезка [a, b]
a = х
0
< х
1
<…< х
i
<…< х
n
= b
получен набор значений y
i
величины y. Если допустить, что между х и y
существует функциональная зависимость y=f(x), можно поставить вопрос о
поиске аналитического представления функции f . Очевидно, что в такой
общей постановке эта задача решается неоднозначно. Точки х
0
, х
1
, …, х
n
в
этом случае называются узлами. Если расстояние h=х
i+1
–х
i
является
постоянным (независящим от i), то сетка значений называется равномерной.
Повод для аппроксимации может возникнуть даже тогда, когда
аналитическое выражение для некоторой функции y=f(x) известно, но
малопригодно для вычислений.
В этих случаях применяется следующий прием – по исходной
информации (таблица значений функции f(x)) строится приближенная
функция
(x), которая в некотором смысле близка к функции f(x) и
аналитическим выражением которой можно воспользоваться для вычисления
приближенного значения f(x), считая, что
f(x) (x).
Чаще всего задача аппроксимации решается с помощью многочленов.
Вычисления значений многочленов легко автоматизировать, легко
вычисляются производная и интеграл от многочлена. Наряду с многочленами
используются ряды Фурье, экспоненциальные, логарифмические и другие
элементарные функции.
Для оценки «близости» функций выбирают тот или иной критерий
согласия. Эти критерии основаны на способах измерения расстояния между
функциями.
111
ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
11.2. Постановка задачи интерполирования функции
Пусть некоторая функция f(x) задана таблично на отрезке [a, b].
x a = x
x
… b = x
n
f(x) y
y
… y
n
Классический подход к решению задачи построения приближающей
функции
(x) основывается на требовании строгого совпадения значений f(x)
и
(x) в точках х
i
, (i1=p0, 1, 2,..., n):
f(x
i
) =
(x
i
), i1=p0, 1, 2, ... , n (11.1)
Нахождение приближенной функции называют интерполяцией (или
интерполированием), а точки x
, x
, ... , x
n
– узлами интерполяции.
Полученную интерполяционную формулу
(x) обычно используют
для приближенного вычисления значений данной функции f(x) для значения
аргумента х, отличных от узлов интерполирования. Такая операция
называется интерполированием функции f(x). При этом различают
интерполирование в узком смысле, когда х[х
0p
,pх
n
], т.е. значение х является
промежуточным между х
0
и х
n
, и экстраполирование, когда х[х
0p
,pх
n
].
Можно сказать, что задача интерполяции обратна задаче
табулирования функции. А именно, при табулировании функции по
аналитическому выражению находятся табличные значения функции, а при
интерполировании, наоборот, по таблице значений функции строится ее
аналитическое выражение.
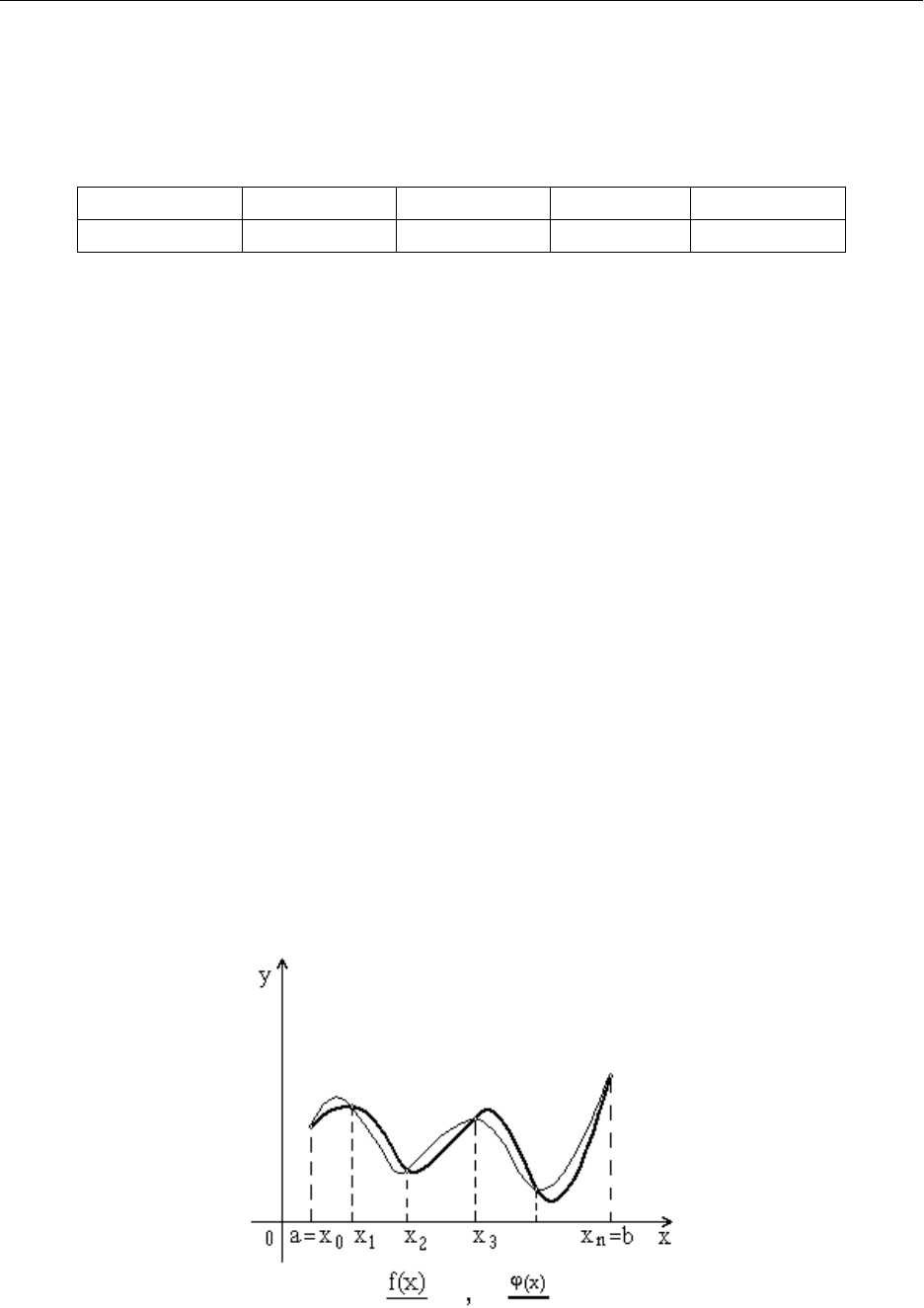
Геометрически интерполирование функции означает, что нужно найти
кривую y=
(x) некоторого определенного типа, проходящую через заданную
систему точек М
i1
(pх
i1
,pу
i1
) (i1=p0, 1, 2, ... , n).
Рис. 11.1. Геометрическая интерпретация интерполирования функции
112
ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
Рассмотрение вопроса о виде интерполирующей функции
(x)
привело к созданию целой теории приближений, весьма сложной и большой
по объему. Мы ограничимся рассмотрением лишь простых случаев: линейная
интерполяция и интерполяция многочленами.
11.3. Линейная интерполяция
Простейшим видом интерполяции является линейная интерполяция.
На каждом из отрезков [х
i1
,pх
i1 +1
] (i1=p0, 1, 2, ... , n1) заменим приближенно
данную функцию линейной, причем значение линейной функции в точках х
i
,
х
ip+1
должны совпадать со значениями f(x) в тех же точках.
Геометрически это означает, что на каждом отрезке [х
i1
,pх
ip+1
]
(i1=p0,p1,p2,p...,pn1) мы заменяем дугу кривой уp= f(x) отрезком прямой,
проходящей через точки М
i
(х
i1
,pу
i
) и М
ip+1
(х
ip+1
, у
ip+1
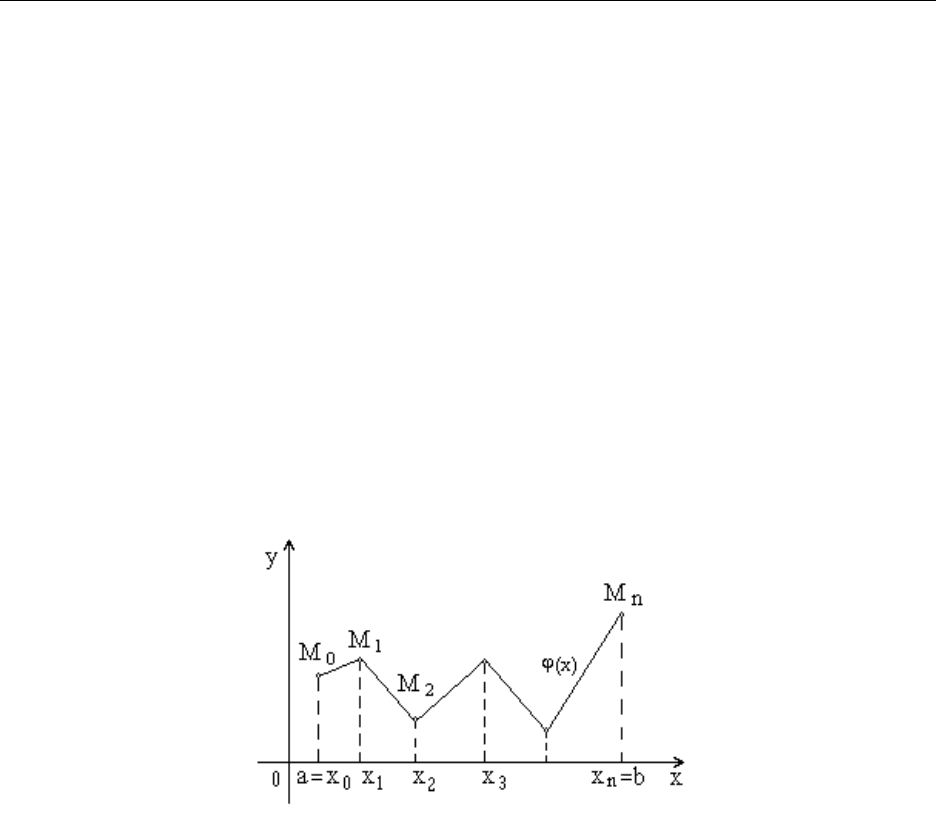
). Таким образом строится
ломанная М
0
, М
1
, М
2
, ... М
n
и мы получаем функцию линейную на каждом
участке [х
i
, х
ip+1
] , i=0, 1, 2, ... , n1.
Рис. 11.2. Линейная интерполяция
Ясно, что при х
i
x х
ip+1
значения построенной функции будут
вычисляться по формуле, которую легко получить, исходя из уравнения
прямой, проходящей через две данные точки М
i
(х
i1
,pу
i
) и М
ip+1
(х
ip+1p
, у
ip+1
):
(11.2)
Представим интерполяционную линейную функцию, график которой
проходит через точки М
i
и М
ip+1
( обозначив
i,ip+1
(х) ) в другом виде, что
иногда оказывается более удобным:
Выражение в квадратных скобках можно представить в виде
определителя второго порядка. Функция
i,ip+1
(х) может быть записана так:
(11.3)
Данная формула вычисления значения функции называется формулой,
полученной по схеме Эйткина.
Если функция достаточно гладкая, то этот метод вычисления f(x) даст
удовлетворительные результаты и часто используется в инженерной
113

ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
практике. Но при решении других задач, например, численное
дифференцирование, погрешности многократно возрастают.
Применение линейной интерполяции приемлемо в том случае, если
значение функции, полученное посредством интерполяции, будет иметь ту
же точность, что и табличные значения функции. Если таблица
удовлетворяет этому требованию, то говорят, что линейная интерполяция для
данной таблицы допустима
6
.
Очевидно, что допустимость линейной интерполяции зависит от шага
таблицы. Если величина достаточно мала, то при изменении х между двумя
соседними табличными значениями ход изменения функции мало отличается
от хода изменения линейной функции. Если шаг недостаточно мал, то ход
изменения функции сильно отклоняется от линейного закона. И поэтому
линейное интерполирование недопустимо.
11.4. Квадратичная интерполяция
Для получения более точных результатов иногда прибегают к
квадратичному интерполированию, заменяя на каждом промежутке (х
ip-
1
,pх
ip+1p
) , i =p1, 2, ... , n1 функцию f(x) квадратным трехчленом
i
(x) таким,
что
i
(х
ip-1p
) = у
ip-1
,
i
(x
i
) = у
i
,
i
(х
ip+1p
) = у
ip+1
Геометрически это означает, что график функции f(x) приближенно
заменяется параболой на каждом промежутке (х
ip-1
,х
ip+1p
), проходящей через
точки М
ip-1
(х
ip-1
,у
ip-1p
), М
i
(х
i
,у
i
), М
i+1
(х
ip+1
,у
ip+1
) , где i=1, 2, ... , n-1.
Для вычисления значений функции, соответствующих
промежуточным значениям аргумента, при квадратичной интерполяции
удобно пользоваться схемой Эйткина, аналогичной схеме Эйткина для
линейной интерполяции.
Итак, даны три значения аргумента х
ip-1p
,pх
i1
,pх
ip+1p
, при которых функция
принимает соответственно значения у
ip-1p
,pу
i1
,pу
ip+1
. Линейная интерполяция на
каждом из участков [х
ip-1p
,pх
i1
]pи [х
ipp
,pх
ip+1
] осуществляется выражениями вида
,
.
Значение функции в точке х, соответствующее квадратичной
интерполяции по указанным трем точкам, получается путем линейной
интерполяции между значениями этих линейных выражений, т.е. по формуле
. (11.4)
6
Методами математического анализа доказывается, что таблица с постоянным шагом допускает линейную
интерполяцию, если соседние табличные разности отличаются друг от друга не более чем на 4 единицы
низшего разряда табличного значения функции.
114

ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
Действительно, так как
ip-1,ip
(х) и
i ,ip+1
(х) являются, как это видно из их
выражений, многочленами первой степени, то
ip-1,ip,ip+1
(х) – многочлен второй
степени относительно х.
Далее
ip-1,ip
(х
ip-1p
) = у
ip-1
,
ip-1,ip
(х
ip
) = у
i1
,
ip,ip+1
(x
i
) = у
i
,
ip,ip+1
(х
ip+1p
) = у
ip+1
.
Поэтому
.
Аналогично
,
.
Итак, мы получили, что многочлен второй степени
ip-1,ip,ip+1
(х)
принимает в точках х
ip-1p
,pх
i1
,pх
ip+1p
, соответственно значения у
ip-1p
,pу
i1
,pу
ip+1
, так, что
он дает требуемую нам параболу.
11.5. Полиномиальная интерполяция. Интерполяционная
формула Лагранжа
Исходя из выше указанного замечания, часто ищут
интерполирующую функцию в виде многочлена степени n:
В постановке задачи требуется совпадение
(x
i
)=у
i
. Из условия Р
n
(x
i
)=
у
i
, i=0, 1, 2, ... , n , получим следующую систему уравнений:
(11.5)
Мы имеем систему n+1 уравнений с n+1 неизвестными c
, c
1
, ... , c
n
.
Определитель имеет вид:
Это определитель Вандермонда. Из курса алгебры известно, что при
x
ip
x
j
, i,1j1=p0, 1, 2, ..., n
и, следовательно, данная система уравнений имеет единственное решение,
т.е. искомый многочлен существует и единственен.
Найдем интерполяционный многочлен Лагранжа. Сначала построим
вспомогательные многочлены L
0
(x), L
1
(x), ... , L
n
(x), каждый из которых
является многочленом степени n и обладает свойством
(11.6)
У каждого многочлена L
i
(x) – n корней: x
, x
, ... , x
i-1
, х
ip+1p
,... , x
n
.
Многочлен можно записать по корням
Чтобы определить А
i
используем условие L
i
(x
i
)=1:
115
ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
откуда
или
Тогда
(11.7)
Многочлен Р
n
(x) можно выразить через L
i
(x):
(11.8)
В самом деле:
степень многочлена не выше n;
в узлах интерполяции x = x
j
при j=0, 1, 2, ... , n:
Итак, по n+1 узлу интерполяции строится интерполяционный
многочлен n-ой степени – интерполяционный многочлен Лагранжа:
(11.9)
f(x) Р
n
(x)
Пример 11.1. Построить интерполяционный многочлен Лагранжа для функции,
заданной таблично:
i x
i
y
i
0 1 12
1 3 4
2 4 6
11.6. Оценка погрешности интерполяционной формулы Лагранжа
Для функции у=f(x) мы построили в 11.5 интерполяционный
многочлен Лагранжа Р
n
(x), принимающий в точках x
, x
, ... , x
n
заданные
значения
.
Возникает вопрос, насколько близко построенный полином
приближается к функции f(x) в других точках, т.е. как велик остаточный член
Для определения погрешности интерполирования положим на
функцию у=f(x) дополнительные ограничения. Предположим, что в
рассматриваемой области a x b изменения х, содержащей узлы
116
ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
интерполирования, функция f(x) имеет все производные f (x), f (x), ..., f
(n+1)
(x) до (n+1)-го порядка включительно.
Введем вспомогательную функцию
, (11.10)
где , и k – постоянный коэффициент, который будет выбран ниже.
Очевидно, что функция u(x) имеет n+1 корень в точках x
, x
, ... , x
n.
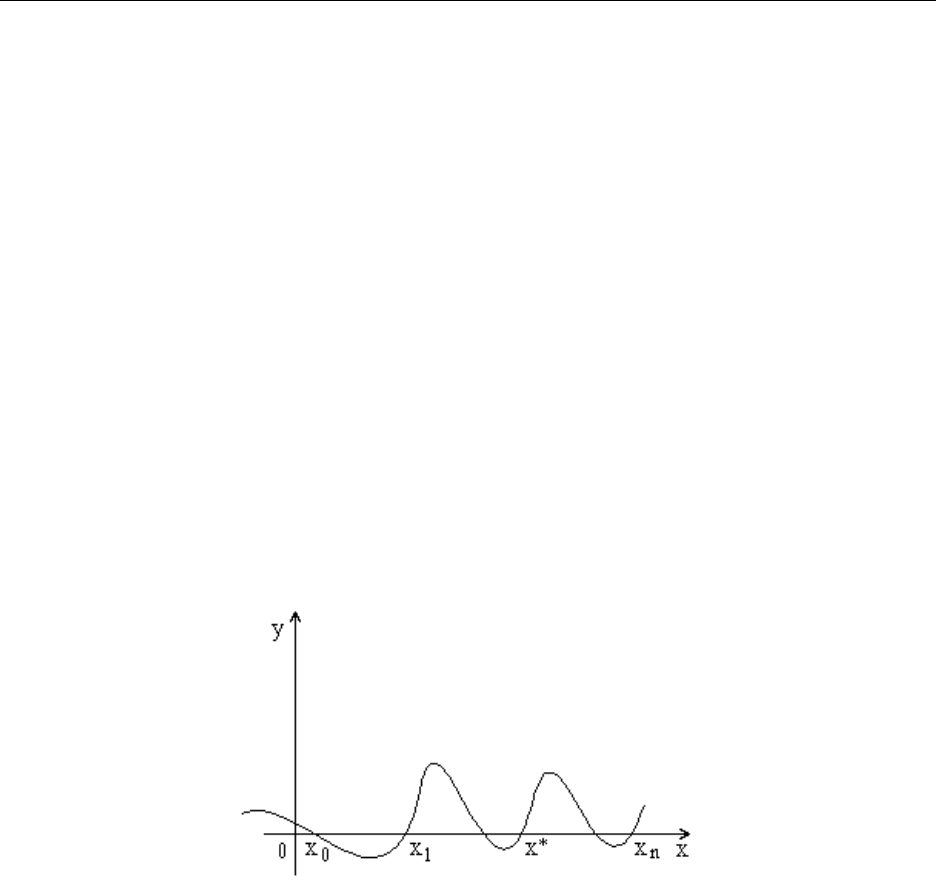
Подберем теперь коэффициент k так, чтобы u(x) имела (n+2)-й корень
в любой точке x* отрезка [a,b], не совпадающей с узлами интерполирования.
Для этого достаточно положить
Отсюда, так как , то
. (11.11)
При этом значении множителя k функция u(x) имеет (n+2) корня на
отрезке [a,b] и будет обращаться в нуль на концах каждого из отрезков
[х
0
,pх
1
], [х
1
,pх
2
], ..., [х
i
,pх*], [х*,pх
i1 +1
], ..., [х
n-1
,pх
n
].
Применяя теорему Ролля к каждому из этих отрезков, убеждаемся, что
производная u(x) имеет не менее n+1 корня на отрезке [a,b]. Применив
теорему Ролля к производной u(x), мы убедимся, что вторая производная
u(x) обращается в ноль не менее n раз на отрезке [a,b].
Продолжая эти рассуждения, придем к заключению, что на
рассматриваемом отрезке [a,b] производная u
(n+1)
(x) имеет хотя бы один
корень, который обозначим через , т.е. u
(n+1)
()=0.
Так как
и
из формулы (1) имеем:
При получаем:
Отсюда
. (11.12)
сравнивая новые части (2) и (3), будем иметь:
117

ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
Теорема о корнях производной (теорема Ролля). Между двумя
последовательными корнями дифференцируемой функции всегда содержится
по меньшей мере один корень ее производной.
Т.е.
. (11.13)
Так как х* произвольно, то формулу (11.13) можно записать:
(11.14)
где зависит от х и лежит внутри отрезка [a,b].
Отметим, что формула (11.14) справедлива для всех точек отрезка
[a,b], в том числе и для узлов интерполирования.
Обозначив через
,
мы получаем следующую оценку для абсолютной погрешности
интерполяционной формулы Лагранжа:
, (11.15)
где
. (11.16)
11.7. Интерполяционные многочлены Ньютона для
равноотстоящих узлов
Часто интерполирование ведется для функций, заданных таблицами с
равноотстоящими значениями аргумента. В этом случае шаг таблицы h=p х
ip+1
–
х
i
, i=0,1,2,...,n1 является величиной постоянной. Для таких таблиц
построение интерполяционных формул (как, впрочем, и вычисление по этим
формулам) заметно упрощается.
Конечные разности. Пусть функция задана таблицей с постоянным
шагом. Разности между значениями функции в соседних узлах интерполяции
называются конечными разностями первого порядка:
y
i
= y
ip+1 –
y
i
, ( i=0,1,2, ...)
Из конечных разностей первого порядка образуются конечные
разности второго порядка:
y
i
= y
ip+1
–
y
i
, ( i=0,1,2, ...)
Продолжая этот процесс, можно по заданной таблице функции
составить таблицу конечных разностей. Конечные разности любого порядка
могут быть представлены через значения функции. Действительно, для
разностей первого порядка это следует из определения. Для разностей
второго порядка имеем:
Аналогично для разностей третьего порядка:
и т.д.
118
