Федченко Г.М. Лекции. Численные методы

Подождите немного. Документ загружается.

ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ

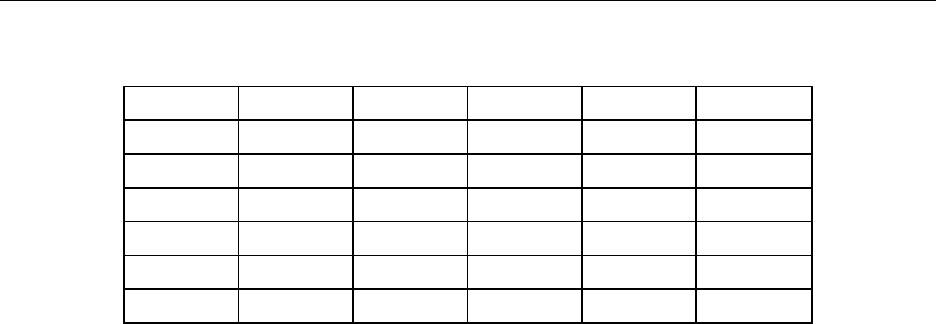
Методом математической индукции можно доказать, что

x y y









...

y









y









y





...

y

...

... ...

Первая интерполяционная формула Ньютона. Пусть для функции, заданной

таблицей с постоянным шагом, составлена таблица конечных разностей.

Будем искать интерполяционный многочлен в виде:

(11.17)

Это многочлен n-ой степени. Значения коэффициентов a

, a

найдем

из условия совпадения значений исходной функции и многочлена в узлах.

Полагая х = х

находим у

= P

) = а

, откуда а

= у

. Далее, придавая х

значения х

и х

, последовательно получаем:

, откуда ;

т.е. , или , откуда

Далее, проведя аналогичные выкладки, можно получить:

;

в общем случае выражение для а

будет иметь вид:

; (11.18)

Подставим теперь (14.2) в выражение для многочлена (14.1):

(14.3)

Практически эта формула применяется в несколько ином виде.

Положим , т.е. х = х

+ ht. Тогда:

и т.д.

Окончательно имеем:

. (11.19)

Формула (11.19) называется первой интерполяционной формулой

Ньютона. Эта формула применяется для интерполирования в начале отрезка

интерполяции, когда t мало по абсолютной величине. Первую

интерполяционную формулу Ньютона называют по этой причине формулой

для интерполирования вперед. За начальное значение x

можно принимать

любое табличное значение аргумента x.

119

ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ

Вторая интерполяционная формула Ньютона. Когда значение аргумента

находится ближе к концу отрезка интерполяции, применять первую

интерполяционную формулу становится невыгодно. В этом случае

применяется формула для интерполирования назад – вторая

интерполяционная формула Ньютона, которая отыскивается в виде:

(14.20)

Как и для первой формулы Ньютона, коэффициенты a

, a

находятся из условия совпадения значений функции и интерполяционного

многочлена в узлах:

(11.21)

Подставляя (14.6) в (14.5) и переходя к переменной , получим

окончательный вид второй интерполяционной формулы Ньютона:

. (11.22)

Пример 14.1. Построить интерполяционный многочлен Ньютона для функции, заданной таблично:

i x

0 1 12

1 3 4

2 5 12

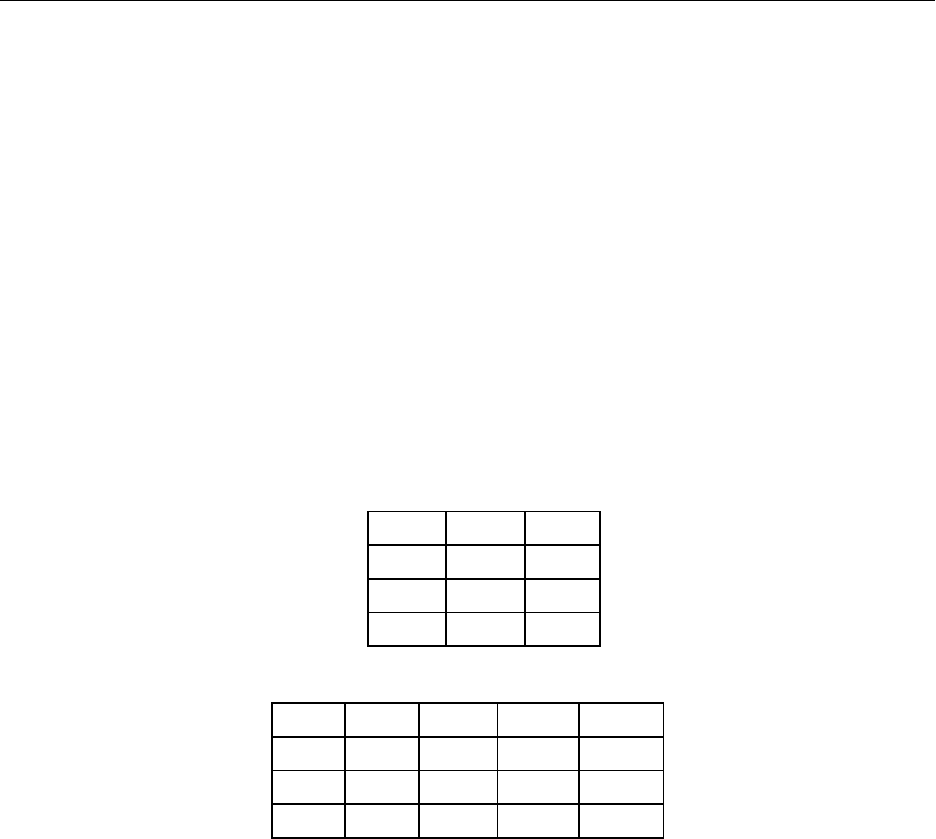
Построим таблицу конечных разностей:

i x

y





0 1 12 –8 16

1 3 4 8

2 5 12

h=2

= 12 – 4(x–1) + 2(x–1)(x–3).

Представим тот же многочлен в форме (14.4). Введем переменную и

получим

= 12 – 8t + 8t(t–1).

11.8. Оценка погрешности интерполяционных формул Ньютона

Если узлы интерполирования x



, x



, ... , x

– равностоящие, причем



– x

= h (i=0,1,2, ..., n–1)

то, полагая

на основании формулы (14.5) предыдущего параграфа получили остаточный

член первой интерполяционной формулы Ньютона

, (11.23)

где некоторое промежуточное значение между узлами интерполирования

120

ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ



, x



, ... , x

и рассматриваемой точкой х, т.е. [a,b].

Аналогично, полагая

получим остаточный член второй интерполяционной формулы Ньютона

, (11.24)

где некоторое промежуточное значение между узлами интерполирования



, x



, ... , x

и точкой х.

Если

то можно записать оценки абсолютных погрешностей интерполирования по

формуле Ньютона:

, (11.25)

, (11.26)

Продемонстрируем связь между конечными разностями и точностью

интерполирования по формулам Ньютона. Примем во внимание, что при

малых значениях h и при условии непрерывности f

(n+1)

(x), учитывая, что

а также, предполагая, что 

n+1

y почти постоянны, можно приблизительно

считать

в этом случае остаточный член первой интерполяционной формулы Ньютона

получит вид:

, (11.27)

, (11.28)

Очевидно, что при составлении интерполяционных формул Ньютона

на практике можно пренебречь членами, в которых соответствующие

конечные разности равны или близки к нулю. Поэтому в практических

вычислениях интерполяционные формулы Ньютона обрывают на членах,

содержащих такие разности, которые в пределах заданной точности можно

считать постоянными.

Формулы (11..27) и (11.28) удобны тем, что позволяют делать оценку

ошибки метода интерполирования без исследования (n+1)-й производной

интерполируемой функции f (в частности, когда аналитическое выражение f

вовсе не известно).

Применим формулу (11.27) к оценке погрешности при линейной

интерполяции. Приняв n=1, получим

Если мы используем интерполяцию для лежащего между точками x





 значения х, то t удовлетворяет условию 0<t<1 и при этих значениях t

справедливо неравенство , то .

121

ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ

Таким образом, абсолютная ошибка линейной интерполяции по

таблице с постоянным шагом и практически постоянными вторыми

разностями не превосходит восьмой части величины второй разности.

Из этого правила мы заключаем, что линейная интерполяция дает

приблизительно на один верный знак больше, чем величина второй разности.

Это означает, что если, например, вторая разность есть величина порядка

десяти единиц последнего знака таблицы, то линейная интерполяция дает

точность порядка единицы последнего знака. Если вторая разность

существенно больше, то линейная интерполяция может оказаться уже

непригодной. Она будет тем более непригодной, если вторые разности на

рассматриваемом участке таблицы заметно изменяются. В таких случаях

требуется интерполяция более высокой степени.

11.9. Экстраполяция. Обратная интерполяция

Интерполяционные формулы могут быть использованы и для

нахождения значений функции, соответствующих значениям аргумента,

находящимся вне пределов таблицы, т.е. для экстраполяции.

Применение интерполяционных формул для экстраполяции ничем не

отличается. Единственным различием является то, что при интерполяции по

первой формуле Ньютона значение t оказывается положительным, а при

экстраполяции – отрицательным. Для второй формулы Ньютона, наоборот,

при интерполяции t отрицательно, а при экстраполяции – положительно.

Таким образом, первая интерполяционная формула Ньютона

применяется для интерполирования вперед и экстраполирования назад, а

вторая – для интерполирования назад и экстраполирования вперед.

Отметим, что экстраполяция, вообще говоря, дает большие ошибки,

нежели интерполяция, и пределы ее применения ограничены.

До сих пор мы рассматривали лишь задачи нахождения значений

функции, соответствующих данным значениям аргумента, отсутствующим в

таблице. Между тем, нередко приходится сталкиваться и с задачами иного,

обратного характера: по таблице функции отыскать значение аргумента х,

которому соответствует данное значение функции, отсутствующее в таблице.

Так поставленную задачу называют задачей обратной интерполяции.

Задачу обратной интерполяции можно легко обратить, считая

значение функции, наоборот, значениями аргумента. Однако, разности

функции не постоянны, поэтому обратная интерполяция приводит к

необходимости интерполировать по таблице, значения аргумента в которой

не является равноотстоящими. По этой причине для обратной интерполяции

применяется обычно интерполяционная формула Лагранжа.

122

ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ

11.10. Контрольные вопросы и упражнения

1. Сформулируйте постановку задачи приближения функции. Задача

аналитического приближения табличной функции в общем виде.

2. Сформулируйте постановку задачи интерполирования табличной

функции и постройте ее геометрическая интерпретация.

3. Сформулируйте задачу полиномиального интерполирования.

Докажите единственность интерполяционного полинома n-ой степени,

построенного по n+1 узлу интерполяции.

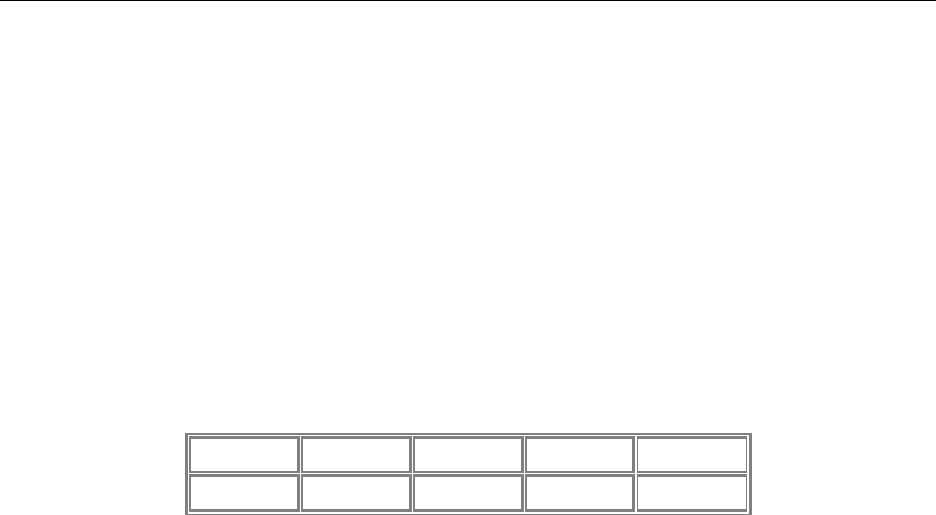
4. По таблице постройте интерполяционный многочлен

x -1 0 1 2

y 4 2 0 1

5. Сформулируйте задачу экстраполирования и пути ее решения.

6. Сформулируйте задачу обратного интерполирования и пути ее

решения.

7. Найдите значения функции y=x

+3 для x=1,2,3,4,5. Постройте таблицу

конечных разностей и постройте многочлены Ньютона по первой и

второй формулам интерполяции.

123

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

Лекция 12

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

12.1. Постановка задачи

Пусть в результате измерений в процессе опыта получена таблица

некоторой зависимости f, а именно, при фиксированных х

, х

, ..., х

имеем у

, ..., у

, полученные экспериментальным путем.

Задача: Найти формулу, выражающую эту зависимость аналитически.

Один из путей решения задачи: интерполирование с помощью

полиномов Лагранжа или линейной интерполяции, где требуется совпадение

значений в узлах интерполяции, но

1) это не означает совпадения функции в промежутках между узлами,

2) значения y

, y

, ..., y

получены экспериментально, а следовательно

являются приближенными, поэтому применение интерполирования не

оправдано.

Поставим задачу: Найти функцию F(x) заданного вида, которая в

точках x

,px

, ..., x

принимает значения как можно более близкие к

табличным значениям y

, y

, ..., y

x x

... x

f(x) y

... y

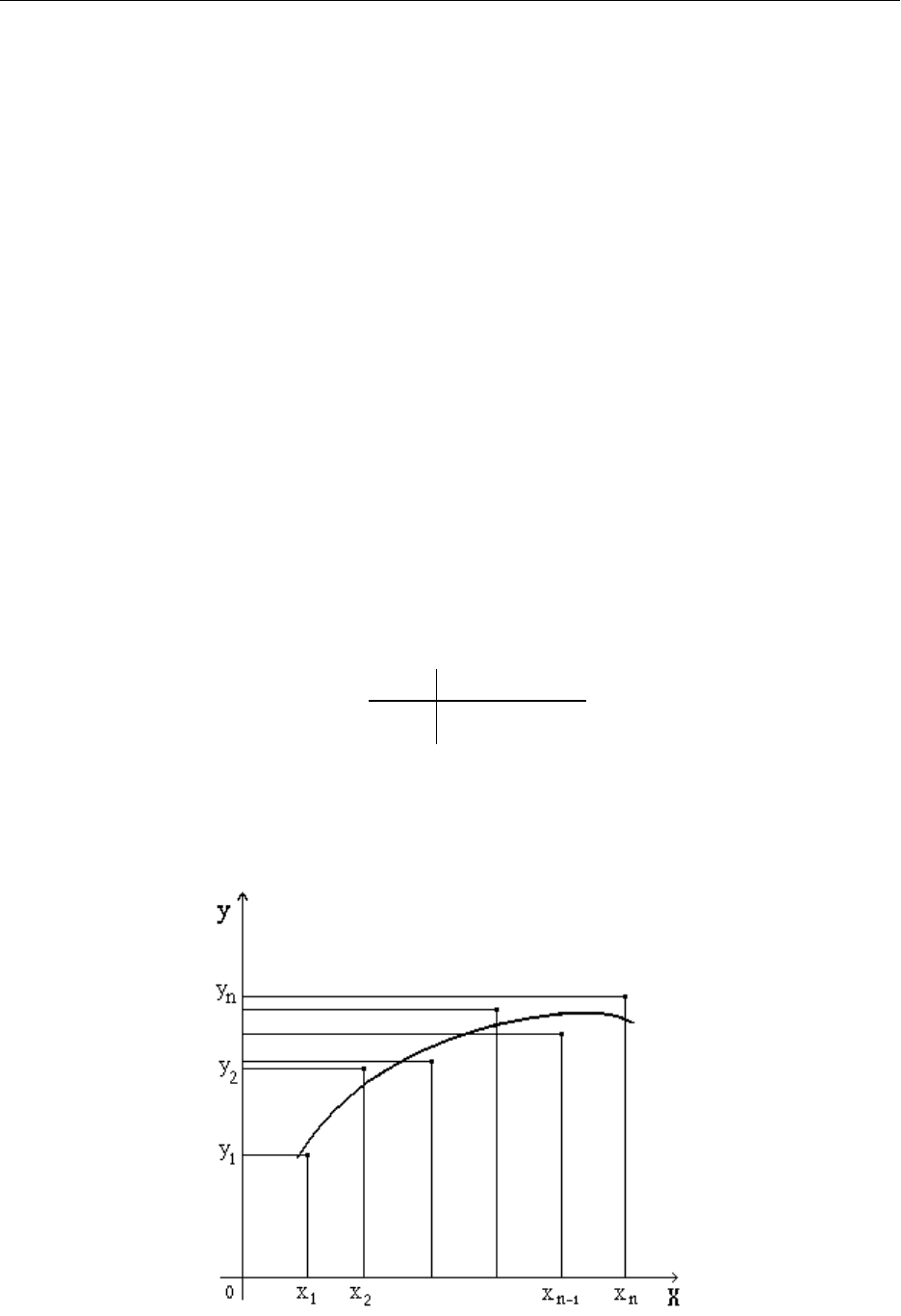
12.2. Геометрическая интерпретация

Практически вид приближающей функции F(x) можно определить

следующим образом. По таблице строится точечный график функции f.

124

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

Затем проводится кривая, по возможности наилучшим образом

отражающая характер расположения точек. По полученной таким образом

кривой устанавливается вид приближающей функции.

Рассмотрим один из самых распространенных способов нахождения

F(x).

Пусть

y y y

n1 2

, ,...,

- значения функции F(x) в точках x

,px

, ..., x

y F x

i i

 ( )

i=1,n

Требование близости табличных значений y

, y

, ..., y

и значений

y y y

n1 2

, ,...,

можно истолковать следующим образом.

Пусть M(y

, y

, ..., y

 

M y y y

n1 2

, ...,

- точки в n-мерном пространстве.

Задача приближения может быть переформулирована следующим образом:

найти такую функцию F заданного вида, чтобы расстояние между точками

было наименьшим. Т.е. (

) должно быть минимальным:

(

) =

(y - y ) + (y - y ) + ... + (y - y )

2 2

n n

 min.

Это требование равносильно следующему

(y - y ) + (y - y ) + ... + (y - y )

2 2

n n

 min. ()

Итак, задача приближения функции f состоит в следующем: для

функции f, заданной таблично, найти функцию F(x) определенного вида так,

чтобы сумма квадратов соответствующих значений () была наименьшей -

отсюда название: метод наименьших квадратов.

В качестве приближающей функции в зависимости от характера

точечного графика функции f часто используют следующие функции:

1) y = ax + b

линейная

5) y =

дробно-линейная

2) y = ax

+ bх +c

квадратичная

6) y =

d +cx

дробно-рациональная

3) y = kx

степенная

7) y = a lnx + b

логарифмическая

4) y = ke

показательная

8) y = a + b

гипербола

где a, b, c, m - параметры.

После того, как определен вид приближающей функции, задача

сводится к определению параметров a, b, c, m.

125

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

12.3. Нахождение параметров приближающей функции в общем

виде

Рассмотрим метод нахождения параметров приближающей функции

на примере приближающей функции с тремя параметрами, т.е.

 

y F x a b c , , ,

Таким образом, имеем:

 

y F x a b c

i i

 , , ,

i=1, 2, ..., n

Сумма квадратов разностей соответствующих значений функций f и F

будет иметь вид:

   

),,(),,,(

cbacbaxFyyy









Эта сумма является функцией



(a,b,c) трех переменных (параметров a, b, c).

Задача сводится к отысканию min



Используем необходимые условия экстремума функции трех

переменных.

,0

















Таким образом, имеем

 

y F x a b c F x a b c

i i a i

i i b i

i i c i

 





 





 



















, , , , , ,

Решив эту систему трех уравнений с тремя неизвестными

относительно параметров a, b, c, получим конкретный вид функции

 

F x a b c, , ,

Изменение количества параметров не приведет к искажению

сущности самого подхода, а выразится лишь в изменении количества

уравнений в системе.

12.4. Нахождение приближающей функции в виде линейной

функции

Будем искать приближающую функцию в виде:

 

F x a b c, , , 

ax + b

1. Найдем частные производные по параметрам

2. Составим систему

126

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

 

y ax b x

y ax b

i i i

i i

   

  















Далее имеем

y x a x b x

y a x nb

i i i i

i i

    

   



















111

Или деля каждое уравнение на n

a x b x x y

a x nb y

i i i i

i i

    

  



















111

Решая систему находим a и b, а следовательно конкретный вид

функции y=ax+b:

a x b x x y

a x nb y

i i i i

i i

    

  



















111

S a S b S

S a nb S

1 2 3

2 4

 











Главный определитель:

   

S S

S n

nS S

1 2

Дополнительные определители:



3 2

3 2 4

  

S S

S n

nS S S



1 3

2 4

1 4 2 3

  

S S

S S S S

127

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ









, ba

128