Федченко Г.М. Лекции. Численные методы
Подождите немного. Документ загружается.


ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
8.8. Контрольные вопросы и упражнения
1. В каких случаях прибегают к численным методам решения нелинейного
уравнения с одним неизвестным?
2. Назовите основные этапы численного решения нелинейного уравнения с
одним неизвестным.
3. В чем заключается этап отделения корней?
4. Как аналитически проверить и уточнить графическое отделение корней?
5. Даны уравнения: а)
0
1
ln
x
x
, б)
01cos3 xx
. Отделите их корни
графически и проверьте результаты аналитически.
6. Приведите примеры уравнения вида P
4
(x)=0, имеющего четыре, три, два
один, ни одного действительных корня, постройте схематично их
графики.
7. Корень некоторого уравнения отделен на отрезке [2; 3]. Определить,
сколько шагов метода половинного деления надо выполнить для
уточнения корня с точностью =0,1; 0,01; 0,001; 10
-6
.
8. Что означает замечание 1 к теореме 8.3?
9. Докажите утверждение, сформулированное в замечании 2 к теореме 8.3.
10.Оформите подробное доказательство теоремы 8.4.
11.Докажите, что при 0<
(x)<1 на [a; b] итерационная последовательность
сходится к t монотонно, а при –1p<p
(x)p<p0 последовательные
приближения колеблются около корня t. Указание: Следует
рассмотреть отдельно случаи x
0p
<pt, x
0p
>pt и воспользоваться теоремой
Лагранжа.
12.Докажите утверждение, сформулированное в третьем способе приведения
уравнения f(x)=0 к виду, удобному для применения метода простой
итерации. При этом
mM
mM
qx
|)(|
. Покажите, что итерационная
последовательность сходится быстрее, чем та, которая получается в
первом способе приведения уравнения к виду x=
(x).
13.Проверьте, какие из представлений, приведенных в примере 8.3 пригодны
для уточнения корня t
1
уравнения x
3
–3x+1=0 методом простой итерации.
Для удачных представлений найдите соответствующие отрезки и
значения q.
89

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
14.Покажите, что уравнение
0ln xx
имеет единственный корень.
Составьте различными способами эквивалентные уравнения вида x=
(x),
удобные для уточнения этого корня методом простой итерации.
15.Докажите утверждение в замечании 3 п .8.7 об оценке погрешности
приближений методом простой итерации.
16.Оцените абсолютные погрешности каждого из приближений,
вычисленных методом простой итерации в примере 8.3.
90
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ (ПРОДОЛЖЕНИЕ)
Лекция 9
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
(ПРОДОЛЖЕНИЕ)
9.1. Метод хорд
Итак, пусть дано уравнение f(x)=0. Будем полагать, что:
1) f непрерывна на отрезке [a; b];
2) f на концах отрезка [a; b] принимает значения
разных знаков, т.е. f(a)pf(b)<0;
3) f
непрерывна и сохраняет постоянный знак на
отрезке [a;pb], т.е. f
(x)>0 (или f
(x)<0) для всех x1[a; b];
4) f
непрерывна и сохраняет постоянный знак на
отрезке [a;pb], т.е. f
(x)>0 (или f
(x)<0) для всех x1[a; b].
Для выполнения приведенных условий иногда приходится сужать
первоначально найденные отрезки изоляции корня.
Возможны четыре случая:
1. f
1>p0, f
1>p0 – функция возрастающая, ее график вогнутый,
2. f
1<p0, f
1<p0 – функция убывающая, ее график выпуклый,
3. f
1<p0, f
1>p0 – функция убывающая, ее график вогнутый,
4. f
1>p0, f
1<p0 – функция возрастающая, ее график выпуклый.
Не теряя общности, в дальнейшем мы будем рассматривать случай 1.
Остальные случаи можно свести к первому, применяя замену f(x) на –f(x)
и/или x на –x, переходя, таким образом, к решению нового уравнения:
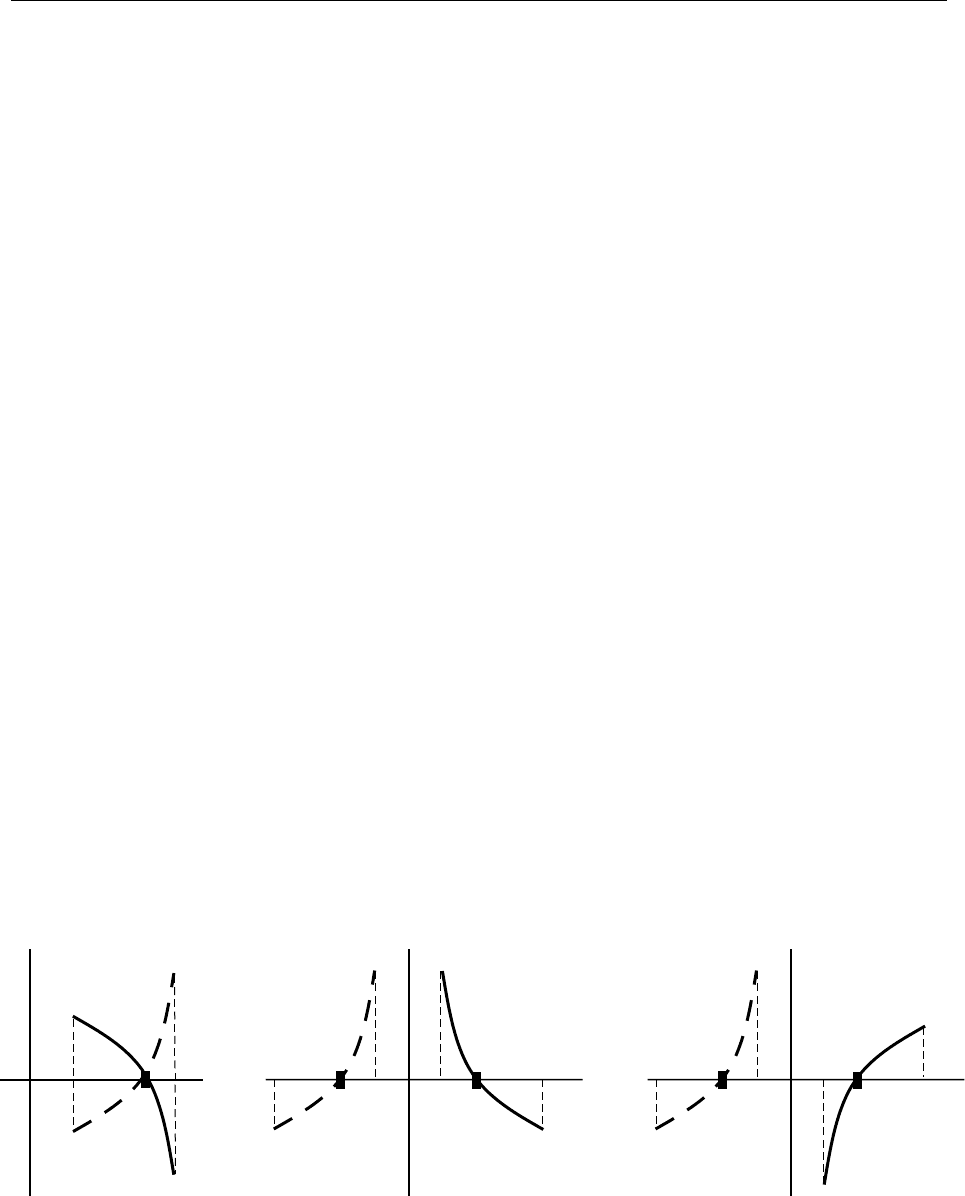
2) 3) 4)
Рис. 9.1
Отметим, что в случае 2) получается уравнение равносильное исходному. В
случаях 3) и 4) корень нового уравнения локализован на отрезке [–b; –a] и
противоположен по значению t – корню исходного уравнения.
91
y=f(x)
a
t
b
y=–f(x)
0
y
x
y=f(x)
a
t
y=f(–x)
0
y
x
–a b
–b
–t
y=f(x)
a
t
y=–f(–x)
0
y
x
–a b
–b
–t
(9.1)
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ (ПРОДОЛЖЕНИЕ)
Упражнение. Докажите аналитически, что при сведении случаев 2), 3), 4) к случаю
1) первая и вторая производная функции, стоящей в левой части
нового уравнения положительны.
Пример 9.1. Геометрически легко локализовать корень уравнения lnpx+x=0 на
отрезке [0,2; 1]. Здесь f(x)=lnpx+x. На данном отрезке
01
1
)(
x
xf
,
0
1
)(
2
x
xf
. Следовательно, имеет место случай 4 и исходное уравнение
можно заменить уравнением вида –f(–x)=0:
– (lnp(– x) – x) = 0 x – lnp(– x) = 0.
Корень полученного уравнения лежит на отрезке [–1; –0,2]. Нетрудно
проверить, что (x – lnp(– x)) и (x1–plnp(–px)) положительны на отрезке [–1; –
0,2].
Рассмотрим метод хорд для уточнения корня уравнения f(x)=0 на
отрезке [a; b], причем f непрерывна на [a; b], f(a)pf(b)<0, f
и f
непрерывны и положительны на [a; b].
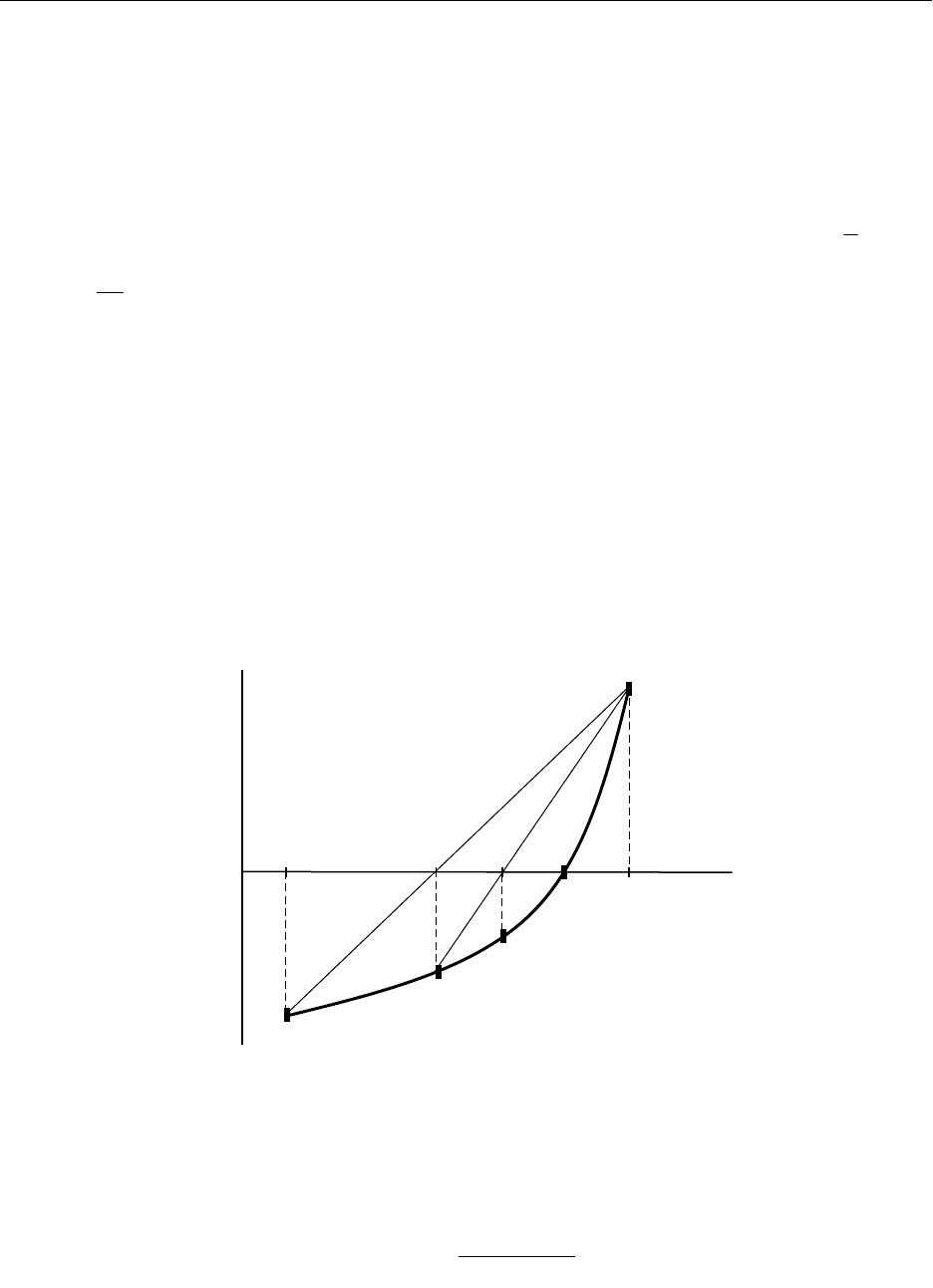
Рис. 9.2. Геометрическая интерпретация метода хорд (f
#>O0, f
#>O0)
Проведем хорду AB и найдем абсциссу x
1
точки ее пересечения с осью Ox:
)()(
))((
1
afbf
abaf
ax
.
Далее построим хорду, соединяющую точки A
1
(x
1
, f(x
1
)) и B(b, f(b)), и
подставим в ее уравнение координаты точки пересечения с осью Ox – (x
2
, 0).
Получим формулу для вычисления абсциссы x
2
точки пересечения A
1
B с Ox:
92
0
a
b
x
1
x
2
x
0
A(a, f(a))
B(b, f(b))
y
x
t
A
1
A
2

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ (ПРОДОЛЖЕНИЕ)
)()(
))((
1
11
12
xfbf
xbxf
xx
.
Продолжая подобным образом и обозначив a через x
0
, получим
итерационную последовательность, вычисляемую по рекуррентной
5)
формуле
,...,2,1,0,
)()(
))((
1
0
n
xfbf
xbxf
xx
ax
n
nn
nn
(9.2)
где правый конец b отрезка [a; b] остается неподвижным, а слева получаем
последовательные приближения, образующие монотонно возрастающую
ограниченную последовательность a = x
0
< x
1
< x
2
< … x
n
< x
n+1
< … < t < b.
Упражнение. Докажите аналитически, что последовательность (x
n
),
порожденная методом хорд для уточнения корня уравнения
f(x)=0, локализованного на отрезке [a;pb], где f
1>p0, f
1>p0,
возрастает и ограничена сверху корнем t.
Теорема 9.1. Пусть корень t уравнения f(x)=0 отделен на отрезке [a;pb],
f(a)pf(b)<0, производные f
, f
непрерывны и положительны на всем [a;pb].
Тогда последовательность (x
n
), определяемая формулами (9.2) сходится к
корню t:
tx
n
n
lim
.
Последовательность (x
n
) в соответствии с теоремой о возрастающей и
ограниченной сверху последовательности имеет предел, не превышающий t.
Пусть
btzx
n
n
lim
. Переходя к пределу в соотношении (9.2), учитывая
непрерывность f и свойства пределов последовательностей, получим
)lim()(
)lim)(lim(
limlim
1
n
n
n
n
n
n
n
n
n
n
xfbf
xbxf
xx
,
)()(
))((
zfbf
zbzf
zz
.
Так как b z, получаем f(z) = 0. Поскольку корень уравнения на отрезке [a;
b] единственный, то t = z.
Замечание: Заметим, что неподвижен тот конец отрезка [a; b], для которого
знак функции f совпадает со знаком ее второй производной f
в этой точке,
а последовательные приближения по ту сторону корня t, где функция f имеет
знак, противоположный знаку ее второй производной f
. Поэтому можно
записать общую рекуррентную формулу метода хорд для любого сочетания
знаков первой и второй производных функции f :
5)
Рекуррентная формула (от лат recurrens – возвращающийся) – формула, выражающая последующий член
последовательности через несколько предыдущих ее членов.
93
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ (ПРОДОЛЖЕНИЕ)
,...,2,1,0,
)()(
))((
1
n
xfcf
xcxf
xx
n
nn
nn
(9.3)
где c тот конец отрезка [a; b], для которого f(c)pf
(c)>0, а в качестве x
0
берется противоположный конец этого отрезка.
9.2. Оценка погрешности приближений по методу хорд
В силу сходимости итерационной последовательности, полученной по
методу хорд, к корню уравнения f(x)=0 при выполнении условий (9.1) ясно,
что рекуррентная формула (9.3) дает нам метод получения приближенного
значения корня с любой наперед заданной точностью >0. Необходимо
оценить точность вычисления приближенного значения корня и выработать
критерий остановки итерационного процесса.
Удобны для этого те методы, которые позволяют сужать общий
интервал (
;
), содержащий корень t и его приближенное значение x
*
. Тогда
|pt1–px
*
|<
1–p
и критерием остановки итераций является выполнение
неравенства |
p–p
|. В методе хорд длины интервалов, содержащих корень
становятся все меньше, но не сходятся к нулю.
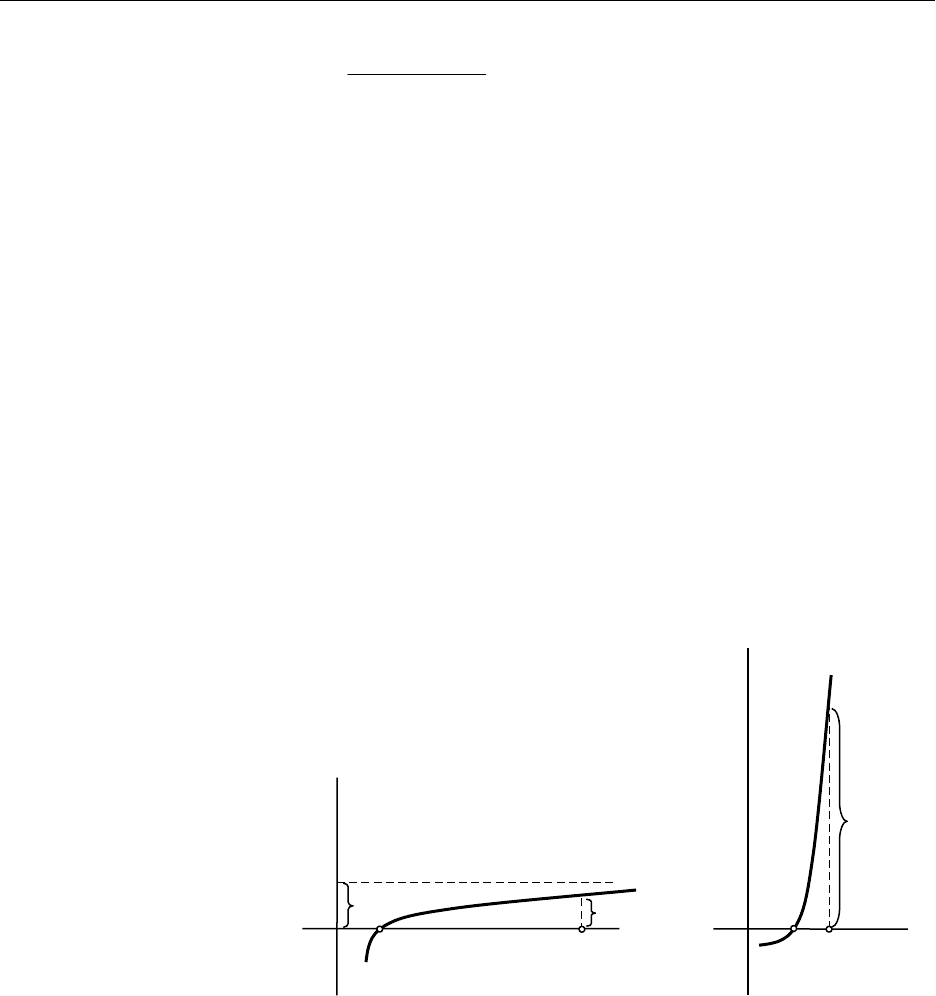
Иногда на практике точность приближенного
значения корня x
*
оценивают по тому, насколько хорошо
он
удовлетворяет данному
уравнению f(x)=0, т.е.
насколько мало
значение |f(x
*
)|. Такой
подход, как показывает
рисунок 9.3, является
неправильным.
Не следует также забывать, что если уравнение f(x)=0 умножить на
произвольное число N0, то получается равносильное уравнение N1f(x)=0,
причем величину |N1f(x
*
)| можно сделать сколь угодно большой или сколь
угодно малой за счет выбора множителя N.
Приведем несколько вариантов оценки точности приближении к
корню, пригодных для метода хорд.
Вариант 1. Пусть корень t уравнения f(x)=0 отделен на отрезке [a; b], и все
члены последовательности (x
n
) приближений к t расположены на этом же
94
f(x
*
)
t
y=f(x)
0
y
x
x
*
Рис. 7.3
f(x
*
)
t
y=f(x)
0
y
x
x
*
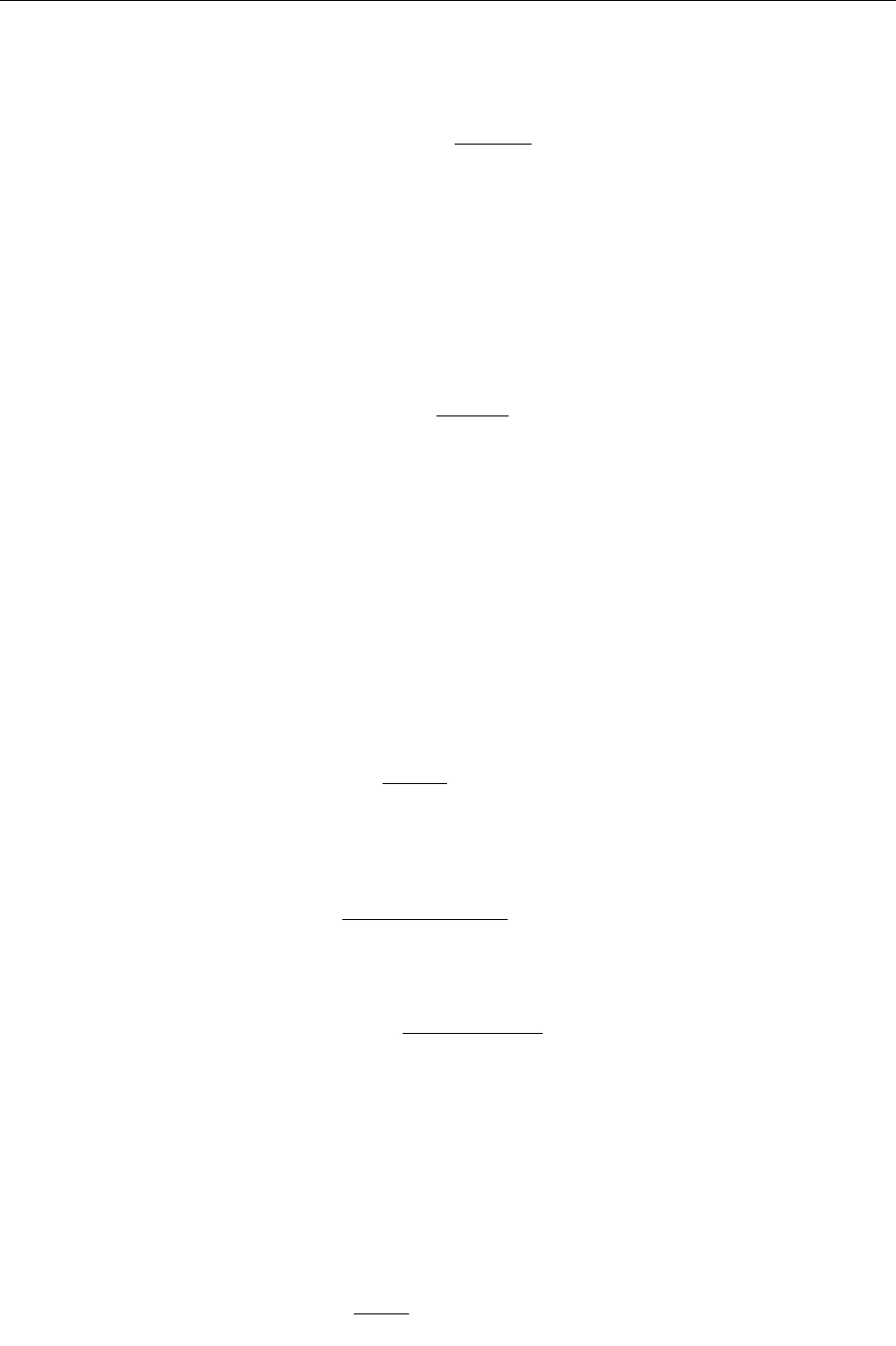
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ (ПРОДОЛЖЕНИЕ)
отрезке. Если производная f
конечна на [a; b] и |pf
(x)p|p m1>p0 для всех
x1p[a;pb], то имеет место неравенство:
,...2,1,0
|)(|
|| n
m
xf
xt
n
n
(9.4)
Возьмем произвольное x
n
. По теореме Лагранжа
))(()()(
nn
xtcfxftf
,
где c1p(t; x
n
)p [a; b]. Перейдем к модулю и, учитывая, что f(t)=0, получим
|||||)(||)(||)()(|
nnnn
xtmxtcfxfxftf
.
Следовательно,
m
xf
xt
n
n
|)(|
||
.
Следующая формула позволяет оценить погрешность приближенного
значения, полученного по методу хорд x
n
, если известны два
последовательных приближения x
n
и x
n-1
.
Вариант 2. Пусть корень t уравнения f(x)=0 отделен на отрезке [a; b], первая и
вторая производные f
и f
непрерывны и сохраняют постоянный знак на
[a;pb], причем 0p<pm1p|pf
(x)p| pM для всех x1p[a; b]. Тогда погрешность
приближения x
n
, полученного по методу хорд, оценивается формулой
,...2,1||||
1
nxx
m
mM
xt
nnn
(9.5)
Доказательство проведем в предположении, что f
(x)p>p0, f
(x)p>p0 для всех
x1p[a; b]. Тогда x
0
=a и приближения x
n
вычисляются по формуле
...,2,1,
)()(
))((
1
11
1
n
xfbf
xbxf
xx
n
nn
nn
Выделив f (x
n-1
) и учитывая, что f(t)=0, получим
)(
)(
)()(
)()(
1
1
1
1
nn
n
n
n
xx
xb
xfbf
xftf
.
По теореме Лагранжа
))(()()(
11
nn
xtcfxftf
,
))(()()(
11
nn
xbdfxfbf
,
где c1p(x
n-1
; t)p [a; b], d1p(x
n-1
; b)p [a; b]. Таким образом,
))(())((
11
nnn
xxdfxtcf
,
11
)(
)(
)(
nnn
xxx
cf
df
t
,
95

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ (ПРОДОЛЖЕНИЕ)
)(
)(
)()(
1
nnn
xx
cf
cfdf
xt
.
Перейдем к модулю
||
|)(|
|)()(|
||
1
nnn
xx
cf
cfdf
xt
.
Так как f
сохраняет постоянный знак на [a;pb], c1p[a; b], d1p[a; b], то
mMmMcfdf
|||)()(|
.
Учитывая, что |pf
(x)p|ppm, окончательно получаем
||||
1
nnn
xx
m
mM
xt
.
Формулы (9.3), (9.4) позволяют вычислять абсолютную погрешность каждого
приближения к корню и выработать критерий остановки итерационного
процесса. Если задана абсолютная погрешность >0, то вычисления в методе
хорд ведутся до выполнения одного из неравенств:
||,
|)(|
1nn
n
xx
m
mM
m
xf
.
Упражнение. Покажите, что если отрезок [a;pb] столь узок, что для значений f
верно неравенство M1p2m, то оценить погрешность приближений в
методе хорд можно по формуле |pt–x
n
p|pp|px
n
–x
n-1
p|.
9.3. Метод Ньютона (касательных)
Пусть для уравнения f(x)=0 выполнены все условия (9.1) на отрезке
[a;pb] (в случае 1). Таким образом, [a;pb] содержит единственный корень
уравнения.
Метод касательных, связанный с именем Ньютона, является одним из
самых известных и быстрых численных методов решения уравнений.
Геометрически он сводится к замене дуги кривой
y=f(x) касательной,
проведенной в некоторой
точке кривой.
96
0
a
b
x
1
x
2
x
0
A
B(b, f(b))
y
x
t
B
1
B
2

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ (ПРОДОЛЖЕНИЕ)
Рис. 9.4. Геометрическая интерпретация метода касательных (f
#>O0, f
#>O0)
Проведем касательную к графику функции y=f(x) в точке B(b, f(b)).
Уравнение касательной имеет вид:
))(()( bxbfbfy
.
Касательная пересекает ось Ox в точке (x
1
, 0). Подставив координаты точки в
уравнение, найдем абсциссу x
1
точки пересечения
)(
)(
1
bf
bf
bx
.
Далее построим касательную в точке B
1
(x
1
, f(x
1
)) и подставим в ее уравнение
координаты точки пересечения с осью Ox – (x
1
, 0). Получим формулу для
вычисления абсциссы x
2
точки пересечения с Ox:
)(
)(
1
1
12
xf
xf
xx
.
Продолжая подобным образом и обозначив b через x
0
, получим
итерационную последовательность, вычисляемую по рекуррентной формуле
...,2,1,0,
)(
)(
1
0
n
xf
xf
xx
bx
n
n
nn
. (9.6)
Таким образом, получаем справа последовательные приближения,
образующие монотонно убывающую ограниченную последовательность b =
x
0
> x
1
> x
2
> … x
n
> x
n+1
> … > t > a.
Для метода касательных важно какая точка x
0
[a; b] выбрана в
качестве начального приближения к корню. Так, если в качестве x
0
для
функции, изображенной на рисунке 4.4 выбрать точку a, то касательная
пересечет ось Ox за пределами [a; b] и x
1
может оказать в области, где не
выполняются условия метода. В качестве начального приближения следует
брать такую точку x
0p
p[a; b], в которой знак функции f совпадает со знаком
ее второй производной f
#: f(x
0
)pf
(x
0
)>0.
97

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ (ПРОДОЛЖЕНИЕ)
Теорема 9.2. Пусть корень t уравнения f(x)=0 отделен на отрезке [a;pb],
f(a)pf(b)<0, производные f
, f
непрерывны и положительны на всем [a;pb].
Тогда последовательность (x
n
), определяемая формулами (4.5) сходится к
корню t:
tx
n
n
lim
.
Сначала методом математической индукции покажем, что
последовательность (x
n
) убывает и ограничена снизу числом t, т.е.
...,2,1,0,
1
n
xt
xx
n
nn
1. При n1=p0 t1< x
0p
=pb, т.к. t p(a; b).
Исходя из формулы (4.5) и свойств функции f1:
0101
00
0
0
01
0
0)(,0)(
)(
)(
xxxx
xfxf
xf
xf
xx
Положим
)(
00
xtxt
и разложим f(t) в ряд Тейлора по степеням
)(
0
xt
,
учитывая существование производных функции f до второго порядка
включительно:
2
0000
))((
2
1
))(()()(0 xtcfxtxfxftf
,
где t1<pc1<px
0
. Так как fp>p0 на всем отрезке [a;pb] третье слагаемое
0))((
2
1
2
0
xtcf
. Учитывая это и знак первой производной f
1:
1
0
0
0
0
000
)(
)(
0)(
0))(()(
x
xf
xf
xt
xf
xtxfxf
.
Таким образом, t1<px
1
1<px
0
.
2. Пусть x
np
>pt. Учитывая, что функция f монотонно возрастает на отрезке
[a;pb]:
0)(
n
xf
.
nnnn
nn
n
n
nn
xxxx
xfxf
xf
xf
xx
11
1
0
0)(,0)(
)(
)(
Полагая
)(
nn
xtxt
и разложив f(t) в ряд Тейлора по степеням
)(
n
xt
,
можно доказать по аналогии с шагом 1, что t1< x
n+1
.
Таким образом, последовательность (x
n
) в соответствии с теоремой о
убывающей и ограниченной снизу последовательности имеет предел, не
меньший t. Пусть
tzx
n
n
lim
. Переходя к пределу в соотношении (9.6),
учитывая непрерывность f и известные свойства пределов, получим
)lim(
)lim(
limlim
1
n
n
n
n
n
n
n
n
xf
xf
xx
,
98
