Федченко Г.М. Лекции. Численные методы
Подождите немного. Документ загружается.


ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ (ПРОДОЛЖЕНИЕ)
)(
)(
zf
zf
zz
.
Так как f
(z) > 0, получаем f (z) = 0. Поскольку корень уравнения на отрезке
[a; b] единственный, то t = z.
9.4. Оценка погрешности приближений по методу касательных
Вариант 1. Формула
,...2,1,0
|)(|
|| n
m
xf
xt
n
n
подходит и для вычисления погрешности приближений к корню t,
полученных по методу касательных, так как все x
n
расположены на отрезке
[a; b] локализации корня.
Получим формулу для оценки погрешности приближенного значения,
полученного по методу касательных x
n
, если известны два последовательных
приближения x
n
и x
n-1
.
Вариант 2. Пусть корень t уравнения f(x)=0 отделен на отрезке [a; b], первая и
вторая производные f
и f
непрерывны и сохраняют постоянный знак на
[a;pb], причемp|pf
(x)p|ppm1>p0,p|pf
(x)p| pM
2
для всех x1p[a; b]. Тогда
погрешность приближения x
n
, полученного по методу касательных,
оценивается формулой
,...2,1)(
2
||
2
1
2
nxx
m
M
xt
nnn
(9.7)
Приближения x
n
в методе касательных вычисляются по формуле
...,2,1,
)(
)(
1
1
1
n
xf
xf
xx
n
n
nn
Следовательно
0))(()(
111
nnnn
xxxfxf
.
Так как все приближения находятся на отрезке [a; b], полагая
)(
11
nnnn
xxxx
, можем записать разложение в ряд Тейлора по степеням
)(
1
nn
xx
с остаточным членом в форме Лагранжа:
2
1111
))((
2
1
))(()()(
nnnnnnn
xxсfxxxfxfxf
.
Учитывая предыдущее равенство, имеем
2
1
))((
2
1
)(
nnn
xxсfxf
.
Перейдем к модулю
99

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ (ПРОДОЛЖЕНИЕ)
2
1
2
2
1
)(
2
)(
2
|)(|
|)(|
nnnnn
xx
M
xx
сf
xf
.
Учитывая оценку погрешности приближения в варианте 1, получаем
искомую оценку
2
1
2
)(
2
||
nnn
xx
m
M
xt
.
Формулы (9.4), (9.7) позволяют вычислять абсолютную погрешность
каждого приближения к корню и выработать критерий остановки
итерационного процесса. Если задана абсолютная погрешность >0, то
вычисления в методе хорд ведутся до выполнения одного из неравенств:
2
1
2
)(
2
,
|)(|
nn
n
xx
m
M
m
xf
.
Упражнение. Покажите, что если отрезок [a;pb] столь узок, что для значений f
, f
верно неравенство M
2p
p2m, то оценить погрешность приближений в
методе касательных можно по формуле |pt-x
np
|pp(x
n
–x
n-1
)
2
.
Замечания:
1. Если отрезок локализации корня в методах хорд,
касательных выбран неудачно, дроби
m
M
m
mM
m 2
,,
1
2
могут оказаться
большими и формулы (9.4), (9.5), (9.7) будут определять грубо
завышенные абсолютные погрешности приближений.
2. В случае когда f
и f
сохраняют постоянный знак на [a;pb],
|pf
1| принимает свои наибольшее и наименьшее значения на концах
отрезка, следовательно, неравенства (9.4), (9.5), (9.7) определяют
зависимость оценок погрешности приближений от свойств функции f на
концах отрезка, а не в непосредственной близости корня, а значит и
зависимость от размера отрезка [a;pb]
9.5. Комбинированный метод
В методах хорд и касательных при выполнении условий (9.1)
приближения расположены с одной стороны корня, что затрудняет оценку их
погрешности. Фактически погрешность приближений часто оказывается
гораздо меньше, чем показывают формулы их оценки, что приводит к
лишним итерационным шагам. Если эти методы применять в сочетании друг
с другом, то от этого недостатка можно избавиться.
В каждом из случаев относительно знаков f
и f
последовательные
приближения по методу хорд и по методу касательных находятся по разные
100
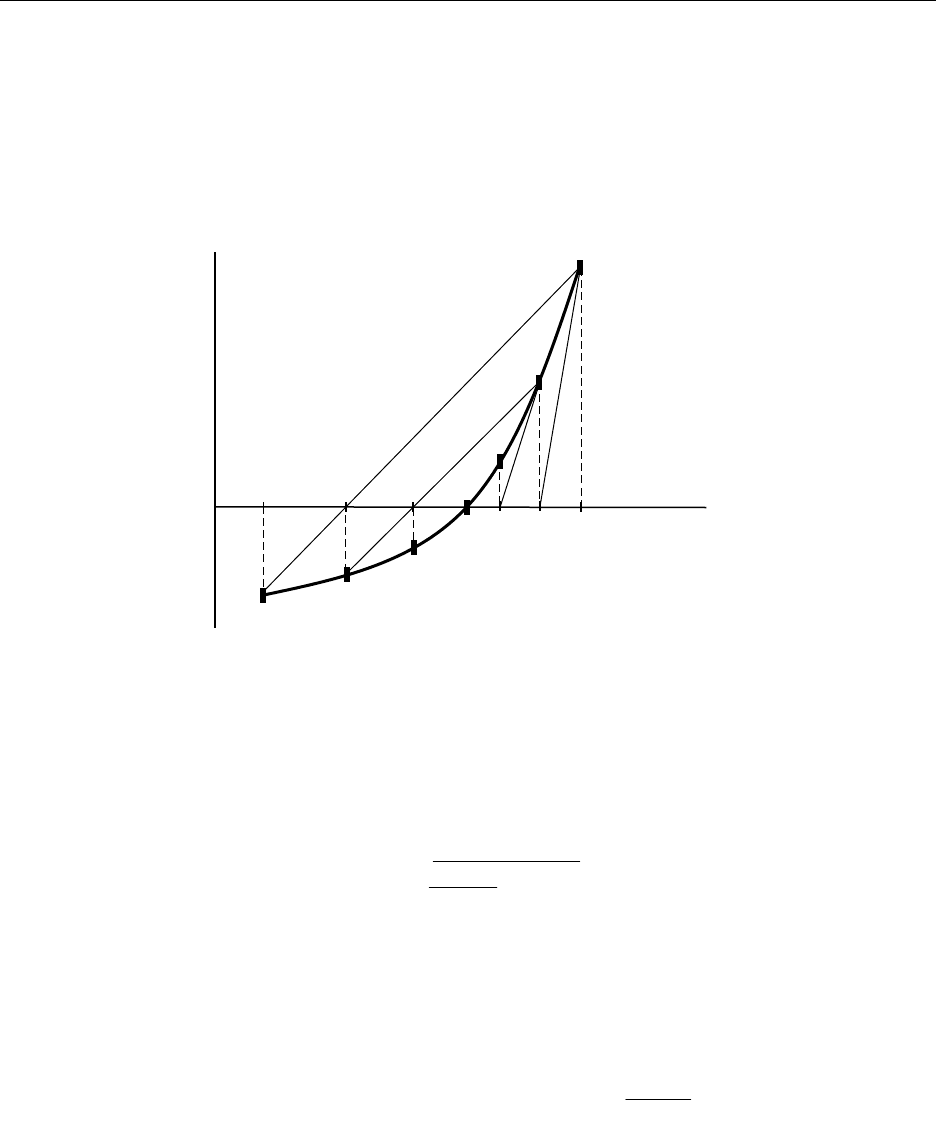
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ (ПРОДОЛЖЕНИЕ)
стороны от корня. Пусть для уравнения f(x)=0 корень локализован на отрезке
[a;pb], причем f – непрерывна, f(a)pf(b)<0, f
, f
– непрерывны и f
1(x)p>p0,
f
1(x)p>p0 для всех x1p[a; b]. На каждом шаге комбинированного метода
будем одновременно строить хорду, находя очередное приближение слева, и
касательную, находя очередное приближение справа.
Рис. 9.5. Геометрическая интерпретация комбинированного метода (f
#>O0, f
#>O0)
Расчетные формулы комбинированного метода имеют вид:
...,2,1,0
)(
)(
)()(
))((
,
1
1
00
n
bf
bf
bb
afbf
abaf
aa
bbaa
n
n
nn
nn
nnn
nn
(9.8)
Согласно теоремам 9.1 и 9.2
ntbta
nn
при,
, причем для любого
n
nn
bta
. Таким образом, как и в методе половинного деления получаем
последовательность вложенных отрезков [a;pb] = [a
0
;pb
0
] [a
1
;pb
1
] [a
2
;pb
2
]
… [a
n
;pb
n
]…, где длина отрезков
0
nn
ab
при n. Процесс уточнения
корня с точностью до
>0 можно остановить как только b
n
– a
n
2. и за
приближенное значение корня взять величину
2
*
nn
ba
x
:
*
xt
с точностью
.
9.5. Контрольные вопросы и упражнения
1. Постройте геометрические интерпретации метода хорд для случаев 2)
f
1<p0, f
1<p0, 3) f
1<p0, f
1>p0, 4) f
1>p0, f
1<p0. Проверьте условие
неподвижности конца отрезка [a; b] для этих случаев.
101
0
a
b
b
1
b
2
b
0
A(a, f(a))
B(b, f(b))
y
x
t
B
1
a
1
a
0
a
2
A
1

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ (ПРОДОЛЖЕНИЕ)
2. Как соотносятся знаки первой и второй производных функции f на
отрезке [a;pb] в случаях, когда в методе хорд неподвижной является точка
a (точка b)?
3. Покажите, что когда знаки f
и f
на [a; b] различны, рекуррентная
формула метода хорд для приближения к корню имеет вид
...,2,1,0,
)()(
))((
1
n
afxf
axxf
xx
n
nn
nn
, (9.9)
при этом левый конец a неподвижен, а начальное приближение x
0
= b.
4. Убедитесь в применимости метода хорд для уравнения
01
1
x
на
отрезке [0,5; 2] изоляции его корня. Запишите соответствующую
рекуррентную формулу метода хорд и вычислите с тремя значащими
цифрами первые два приближения к корню x
1
, x
2
.
5. Для уравнений: а)
05,0arctg xx
, б)
xx sin1
найдите отрезки
изоляции корней, где применимы методы хорд и касательных. Выберите
для уточнения каждого корня соответствующее уравнение и отрезок так,
чтобы значения первой и второй производных функции f были
положительны на этом отрезке.
6. Почему обращение в 0 первой производной f
в точке отрезка [a;pb]
делает неприменимым метод касательных? Является ли это препятствием
для применения на этом отрезке метода хорд? Пояснение
проиллюстрируйте графически.
7. Почему обращение в 0 второй производной f
в точке отрезка [a;pb]
делает неприменимым метод касательных? Является ли это препятствием
для применения на этом отрезке метода хорд? Пояснение
проиллюстрируйте графически.
8. Постройте геометрические интерпретации метода касательных для
случаев 2) f
1<p0, f
1<p0, 3) f
1<p0, f
1>p0, 4) f
1>p0, f
1<p0. Убедитесь
графически, что когда f
и f
одного знака на отрезке [a; b], следует
брать x
0
=pb, а если разных знаков, то x
0
=pa.
9. Докажите теорему 9.2 для другой комбинации знаков f
и f
на отрезке
[a;pb].
10. Если производная f
(x) мало изменяется на отрезке [a; b], можно
применять упрощенную рекуррентную формулу метода касательных,
выбрав подходящее начальное приближение x
0
:
...,2,1,0,
)(
)(
0
1
n
xf
xf
xx
n
nn
(9.10)
102

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ (ПРОДОЛЖЕНИЕ)
(модифицированный метод Ньютона). В этом случае не надо каждый
раз вычислять значение f
(x
n
). Постройте геометрическую
интерпретацию.
11. Сформулируйте и докажите соответствующую теорему о сходимости
итерационной последовательности для (x
n
), полученной с помощью
формул (4.9).
12. Убедитесь в применимости метода касательных для уравнения
033
2
x
на отрезке [0,1; 2] изоляции его корня. Запишите рекуррентную
формулу метода касательных и, выбрав соответствующее начальное
приближение, вычислите с тремя значащими цифрами первые два
приближения к корню x
1
, x
2
и их абсолютные погрешности.
13. Постройте геометрические интерпретации комбинированного метода
для случаев 2) f
1<p0, f
1<p0, 3) f
1<p0, f
1>p0, 4) f
1>p0, f
1<p0.
14. Как изменится комбинированный метод, если в формулах (9.8)
изменить порядок вычисления приближений a
n
и b
n
? Постройте
геометрическую интерпретацию комбинированного метода уточнения
корня, задаваемого следующими рекуррентными формулами:
...,2,1,0
)()(
))((
)(
)(
,
1
1
1
1
00
n
afbf
abaf
aa
bf
bf
bb
bbaa
nn
nnn
nn
n
n
nn
(9.11)
103

РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Лекция 10
РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
10.1. Постановка задачи
Решение систем нелинейных уравнений является в общем случае
задачей несравненно более сложной, чем решение систем линейных
уравнений. Не существует методов, которые гарантировали бы успех
решения любой такой задачи.
Наибольшую проблему представляет задача отделения решений
(корней). Для системы уравнений с n неизвестными необходимо, во-первых,
определить, сколько у нее решений, а во-вторых, выделить области n-
мерного пространства, в каждой из которых локализовано одно и только
одно решение. После этого можно находить решение с заданной точностью.
Для отделения корней общих методов, гарантирующих успех, не существует.
Для системы двух неизвестных можно пытаться геометрически проводить
локализацию решений. При решении прикладных задачах, в которых
моделируется какой-то объект или процесс, можно исходить из
содержательных условий модели.
Далее мы будем исходить из предположения, что задача отделения
корней решена и имеется достаточно малая область n-мерного пространства,
в которой находится корень, подлежащий уточнению.
Пусть требуется решить систему уравнений
, (10.1)
где f
1
, f
2
, …, f
n
– заданные вещественнозначные функции n вещественных
переменных x
1
, x
2
, …, x
n
. Обозначив
, = , ,
систему (10.1) можно записать в векторной форме
F(x)=0, (10.2)
где F – векторная функция векторного аргумента. Таким образом, задачу
(10.1) можно рассматривать как задачу о нулях нелинейного отображения
F:, т.е. как обобщение задачи решения нелинейного уравнения f(x)=0 на
многомерный случай.
10.2. Метод простой итерации
104

РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Метод простой итерации для решения системы нелинейных
уравнений аналогичен методам простой итерации, рассмотренным ранее для
нелинейных уравнений и СЛАУ. На первом шаге система (10.1)
преобразуется к равносильной системе вида
. (10.3)
Или в векторной форме:
x =
(x). (10.4)
Таким образом задача сводится к задаче о неподвижной точке нелинейного
отображения
: в пространстве . Задав начальное приближение для
вектора решения, строится итерационная последовательность с помощью
рекуррентного соотношения
=
(), k=1, 2, …, (10.5)
которое определяет метод простой итерации или метод
последовательных приближений для задачи 10.1.
Если отображение
является сжимающим в некоторой окрестности
корня, начальное приближение лежит в той же окрестности и итерации не
выходят за ее пределы, то последовательность сходится и ее предел является
решением системы (10.3), а значит и исходной системы (10.1).
Требование сходимости итерационного процесса требует
конкретизации, придания ему реально проверяемого вида.
Теорема 10.1. (достаточное условие сходимости метода простых итераций)
Пусть вектор-функция
(x) и замкнутое множество MD
таковы, что
1) xM:
(x)M;
2) q<1: x, x; \s\up6((M ||
(x) –
( x; \s\up6(()|| q∙|| x – x; \s\
up6((||.
Тогда
(x) в M имеет единственную неподвижную точку x
*
и
последовательность , определяемая методом простой итерации при x
(0)
M
сходится к x
*
и справедливы оценки
kN. (10.6)
Условия 1) и 2) неконструктивны, трудно проверяемы. Больший
интерес для приложений может представить следующая теорема.
Теорема 10.2. (достаточное условие сходимости метода простых итераций)
Если вектор-функция
(x) непрерывно дифференцируема на множестве
MD
и для xM ||
(x)|| q < 1, то итерационная последовательность
метода простой итерации сходится к x
*
– решению исходной системы
уравнений x =
(x).
(x) – матрица Якоби:
105
РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
.
Пример 10.1. Пусть задана система уравнений
(10.7)
Представим ее в виде 10.3, отделим ее решения и построим
соответствующую итерационную последовательность с каким-либо
начальным вектором.
Наиболее очевидным вариантом приведенной системы здесь может
быть такой:
(10.8)
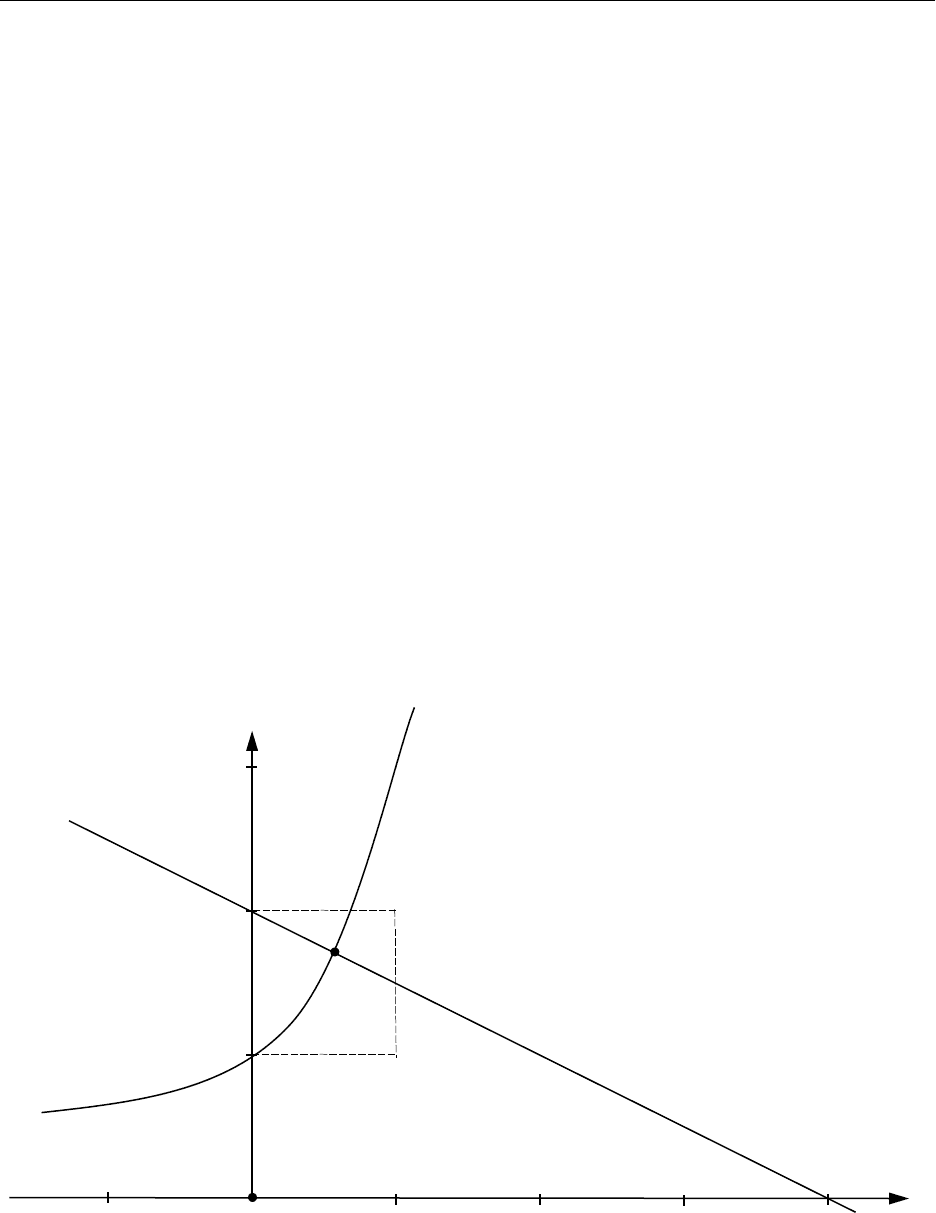
Изобразим линии, задаваемые уравнениями y=e
x
и x=4–2y.
Очевидно, что они пересекаются в единственной точке,
расположенной внутри квадрата M={(x,y): 0 x1, 1y2}.
, ||
|| > 1 на множестве M,
106
x
y
O
y=e
x
x=4–2y
1

РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
следовательно, построить сходящуюся итерационную последовательность не
удастся.
Приведем систему (10.7) к виду (10.4) другим способом:
(10.9)
и на множестве M={(x,y): 0 x1, 1.01y2} ||
|| < 1.
Следовательно, можно построить сходящуюся итерационную
последовательность.
Выберем в качестве начального приближения x
(0)
=1, y
(0)
=2.
10.3. Метод Зейделя
Нередко сходимость метода простой итерации можно улучшить, если
вновь вычисленные значения компонент вектора неизвестных немедленно
включить в расчет. Такая модификация называется методом Зейделя.
Итерационный процесс примет вид
. (10.10)
где k=1, 2, …, а – начальное приближение.
, i=1,…,n.
Пример 10.2. Построим итерационную последовательность метода Зейделя
для системы из примера 10.1, приведенной к виду 10.9.
Можно поставить задачу отыскания оптимальной на каждой итерации
последовательности уточнения компонент вектора решения. Общих
подходов построения оптимальной последовательности нет. На практике
иногда используется упорядочение неизвестных по убыванию разности их
значений на двух последовательных итерациях
10.4. Метод Ньютона
Очевидный недостаток метода простой итерации – необходимость
приведения системы к виду, пригодному для итераций. При решении систем
нелинейных уравнений часто используют метод Ньютона, являющийся
обобщением метода касательных, применяемого для решения нелинейных
уравнений. Существенную роль в этом методе играет матрица Якоби
(якобиан) функционала F:
107

РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
.
Очевидно, что построить ее можно лишь при условии, что каждая из
функций, входящая в систему (12.1), дифференцируема по каждой из
переменных.
Напомним, что метод касательных применительно к одному
уравнению f(x)=0 заключается в построении итерационной
последовательности
)(
)(
1
k
k
kk
xf
xf
xx
.
Обобщением этой формулы на систему уравнений является формула
, k=0, 1, 2, … (12.12)
Если начальное приближение выбрано достаточно близко к решению
системы, то итерационная последовательность сходится к этому решению.
Если задана абсолютная погрешность приближенного решения
системы , то в соответствии с эмпирическим правилом процесс итерации в
большинстве случаев можно остановить, если
.
Метод Ньютона весьма трудоемок, поскольку на каждом шаге
итерационного процесса необходимо найти матрицу, обратную матрице
Якоби. Чаще всего для этого используют метод Гаусса. Тем не менее, для
системы из небольшого количества уравнений можно найти обратную
матрицу аналитическим методом, известным из курса алгебры.
В частности, рассмотрим решение системы из двух уравнений
. (12.13)
Тогда матрица Якоби – матрица второго порядка:
,
а обратная матрица имеет вид
, где . (12.14)
Итерационные формулы (12.12) в этом случае примут вид,
непосредственно пригодный для вычислений:
, k=0, 1, 2, … (12.15)
Верхний индекс (k) означает, что соответствующая величина вычисляется в
точке (x
k
, y
k
).
Пример 12.3. Рассмотрим решение методом Ньютона системы уравнений
, k = 0, 1, 2, …
108
