Федченко Г.М. Лекции. Численные методы
Подождите немного. Документ загружается.

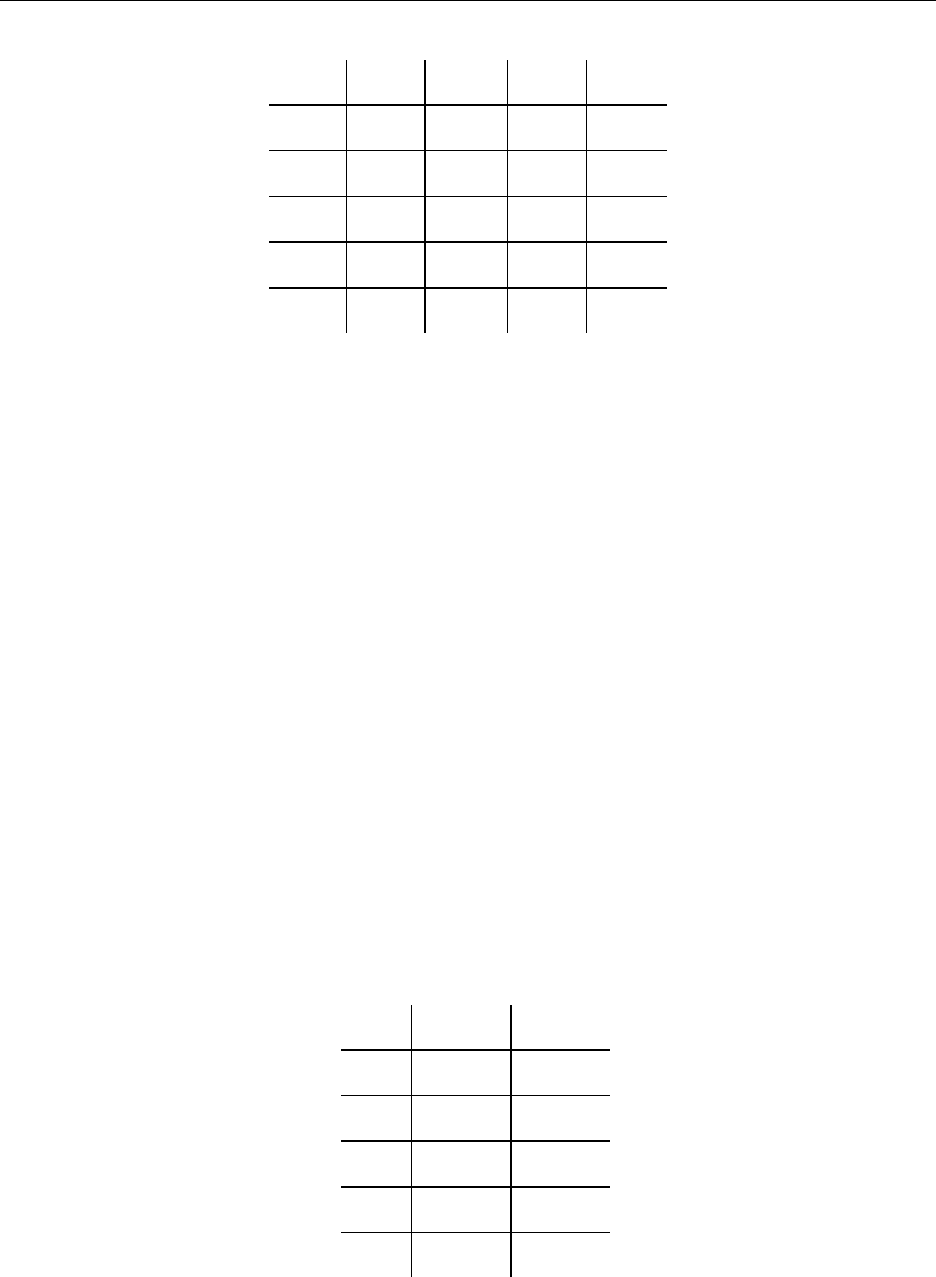
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Пример. n=4
i x
i
y
i
x
i
∙y
i
x
i
2
0 1 0 0
1 3 3 1
3 7 21 9
5 9 45 25
9 20 69 35
35 9 69
9 4 20
a b
a b
59a=96
a=96/591,6 , b=(20-1,69)/41.4
y=1.6x+1.4
12.5. Нахождение приближающей функции в виде других
элементарных функций
Покажем, что нахождение приближающей функции в виде других
элементарных функций сводится к нахождению параметров линейной
функции.
1. Логарифмическая функция y=a ln(x)+b.
Сделаем подстановку u=ln(x) и получим y=au+b, отсюда следует, что
для нахождения коэффициентов a, b нужно воспользоваться новой таблицей
значений аргументов.
x
i
ln(x
i
) y
i
x
1
ln(x
1
) y
1
x
2
ln(x
2
) y
2
. . .
. . .
x
n
ln(x
n
) y
n
2. Гипербола y = a + b.
Сделаем замену u=и перейдем к линейной функции y=au+b, будем
рассматривать таблицу
129
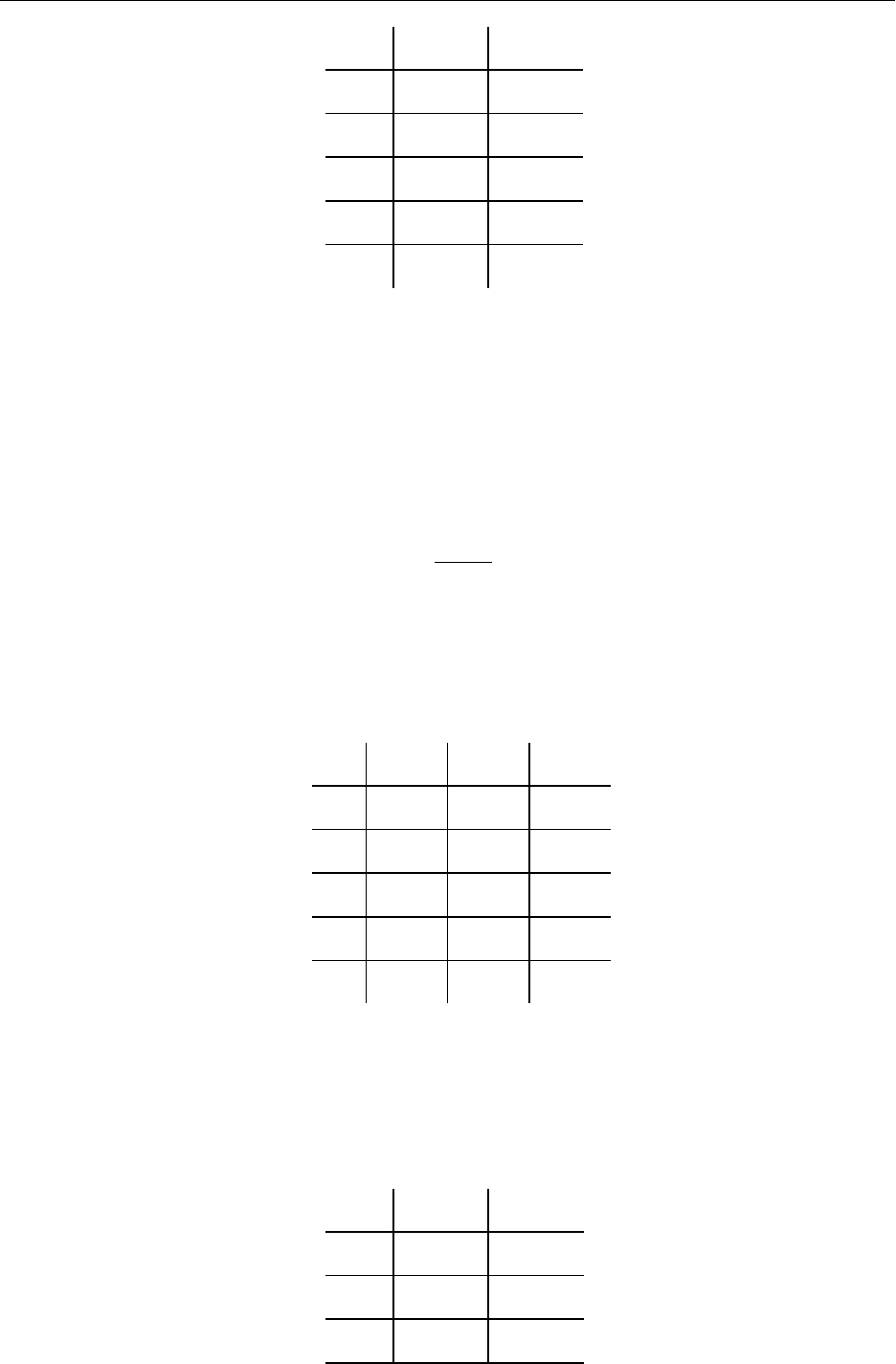
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
xi 1/xi yi
x1 1/x1 y1
x2 1/x2 y2
. . .
. . .
xn 1/xn yn
3. Дробно-линейная функция y=.
Перепишем в виде: = ax+b
Из последнего равенства следует, что для нахождения параметров a, b
по заданной таблице нужно составить новую, где y
i
заменить на обратные им
и после этого получим приближенную функцию вида ax+b, затем найденные
значения подставим в формулу.
4. Дробно-рациональная функция y =
d +сx
x
Сделаем преобразования:
1/y=(cx+d)/x
1/y=c+d/x, 1/x=u
1/y=du+c
Для нахождения параметров a=d, b=c будем работать с таблицами
x
i
1/x
i
y
i
1/y
i
x
1
1/x
1
y
1
1/y
1
x
2
1/x
2
y
2
1/y
2
. . . .
. . . .
x
n
1/x
n
y
n
1/y
n
5. Показательная функция y = ke
mx
Прологарифмируем обе части (значение y
i
>0, i)
ln(y)=ln(k)+mx
Для нахождения коэффициентов a=m, b=ln(k) нужно воспользоваться
новой таблицей значений аргументов.
x
i
x
i
ln(у
i
)
x
1
x
1
ln(у
1
)
x
2
x
2
ln(у
2
)
. . .
130

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
. . .
x
n
x
n
ln(у
n
)
Таким образом, получили
m=a, b=ln(k) k=e
b
.
6. Степенная функция y=kx
m
Прологарифмируем обе части (значение y
i
>0, x
i
>0 i):
ln(y)=ln(k)+m·ln(x), сделаем замену u=ln(x)
ln(y)=m·u + ln(k)
x
i
ln(x
i
) y
i
ln(y
i
)
x
1
ln(x
1
) y
1
ln(y
1
)
x
2
ln(x
2
) y
2
ln(y
2
)
. . . .
. . . .
x
n
ln(x
n
) y
n
ln(y
n
)
После нахождения параметров a, b найдем m=a, k=e
b
и подставим в
исходное уравнение.
12.6. Контрольные вопросы и упражнения
1. Сформулируйте постановку задачиp приближения функции по методу
наименьших квадратов.
2. Сформулируйте алгоритм нахождения параметров линейной
зависимости по методу наименьших квадратов.
3. Сформулируйте алгоритм нахождения приближающей функции по
методу наименьших квадратов в нелинейном виде.
4. Функция y=y(x) задана таблицей своих значений:
x -1 0 1 2
y 1.8 2.4 2.2 2
Постройте многочлены нулевой и первой степени, приближающие
функцию по методу наименьших квадратов. Определите величину средне-
квадратичного отклонения. Постройте на одном чертеже точечный график
функции и графики многочленов.
131

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
132

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
Лекция 13
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
13.1. Постановка задачи
Если функция f(х) непрерывна на отрезке [a,b] и известна ее
первообразная F(x), то определенный интеграл от этой функции в пределах
от a до b может быть вычислен по формуле Ньютона-Лейбница
где .
Но часто возникают ситуации, когда вычислить интеграл можно
только с помощью численных методов:
1) F(x) не выражается через элементарные функции.
;
2) F(x) существует и выражается через элементарные функции, но ее
сложно найти
;
3) Найдена F(x), но сложно вычислить ее значение;
4) f(х) задана таблично или графиком.
Итак, как вычислить .
Обычный прием состоит в том, что данную функцию f(х) на
рассматриваемом отрезке [a,b] заменяют интерполирующей функцией P
n
(x)
простого вида, а затем приближенно полагают:
.
Функция P
n
(x) должна быть такова, чтобы интеграл вычислялся
непосредственно.
Можно использовать интерполяционный многочлен P
n
(x) различной
степени n, n =
13.2. Формулы прямоугольников
При n=
Для построения Р
0
(х) требуется одна точка (х
0
, f(х
0
) ).
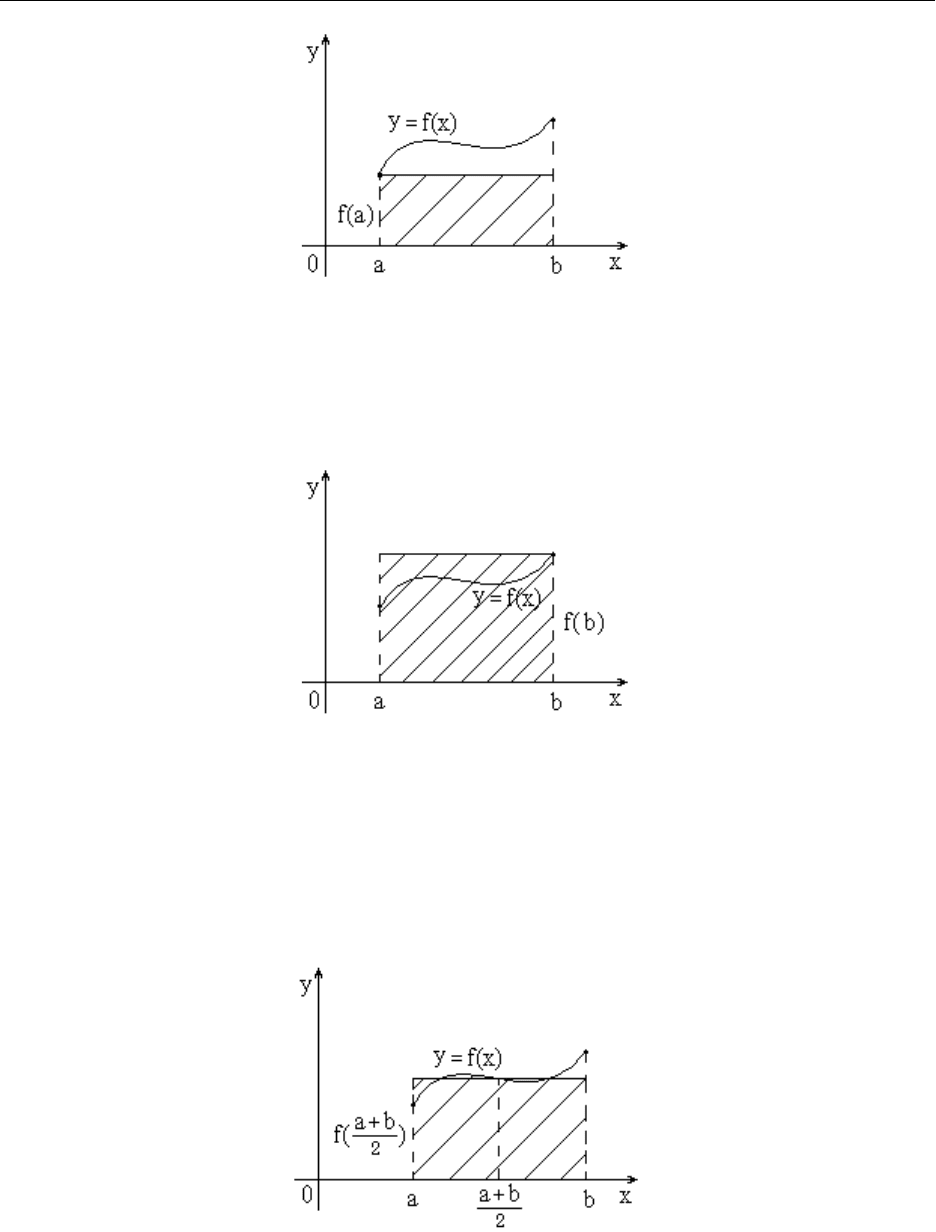
Формула левых прямоугольников:
( а, f(а) )
Геометрическая иллюстрация
133
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
Формула правых прямоугольников:
( b, f(b) )
Геометрическая иллюстрация
Формула центральных прямоугольников:
Геометрическая иллюстрация
13.3. Формула трапеций
При n=
Для построения Р
1
(х) требуется две точки:
134
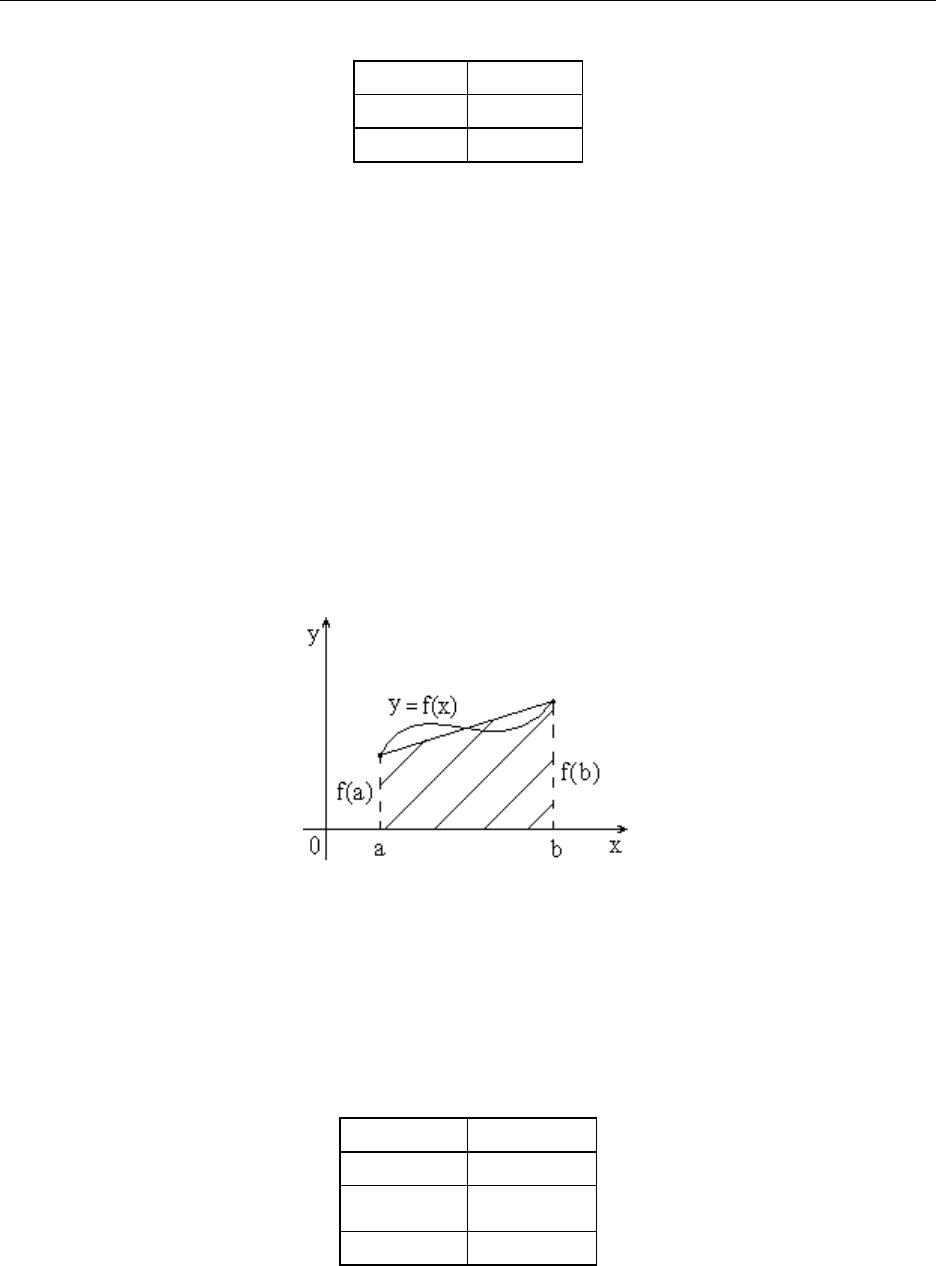
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
х у
х
0
=а у
0
=f(а)
х
1
=b y
1
=f(b)
Геометрическая иллюстрация
13.4. Формула Симпсона
При n=
Для построения Р
2
(х) требуется три точки:
х у
х
0
=а у
0
=f(а)
х
2
=b у
2
=f(b)
135

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
136
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
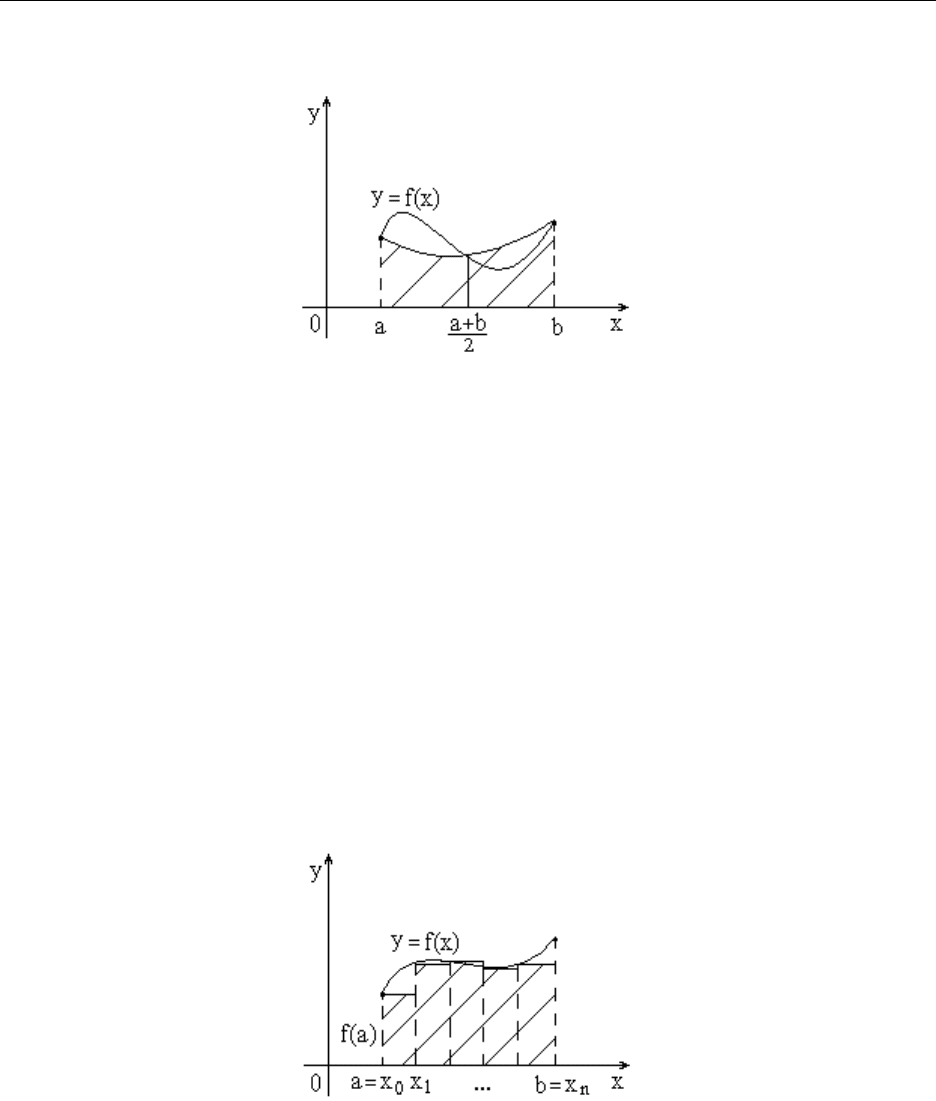
Геометрическая иллюстрация
13.5. Обобщенные формулы
На практике обычно пользуются обобщенными формулами, т.к. [a,b]
может быть большим и, следовательно, большой и погрешность вычисления
интеграла по формулам прямоугольников, трапеции и Симпсона.
Как же добиться повышения точности вычисления?
[a,b] разбивают на n равных частей точками a=x
0
x
1
... x
n
=b, и на
каждом отрезке [x
i
, x
i+1
] применяется конкретный метод прямоугольников,
трапеции или Симпсона, результаты суммируются, пользуясь условием
аддитивности определения интеграла.
Величина - шаг интегрирования, x
i
=x
0
+ih , где .
Обобщенная формула левых прямоугольников
Геометрическая иллюстрация
Введем обозначение :
(13.1)
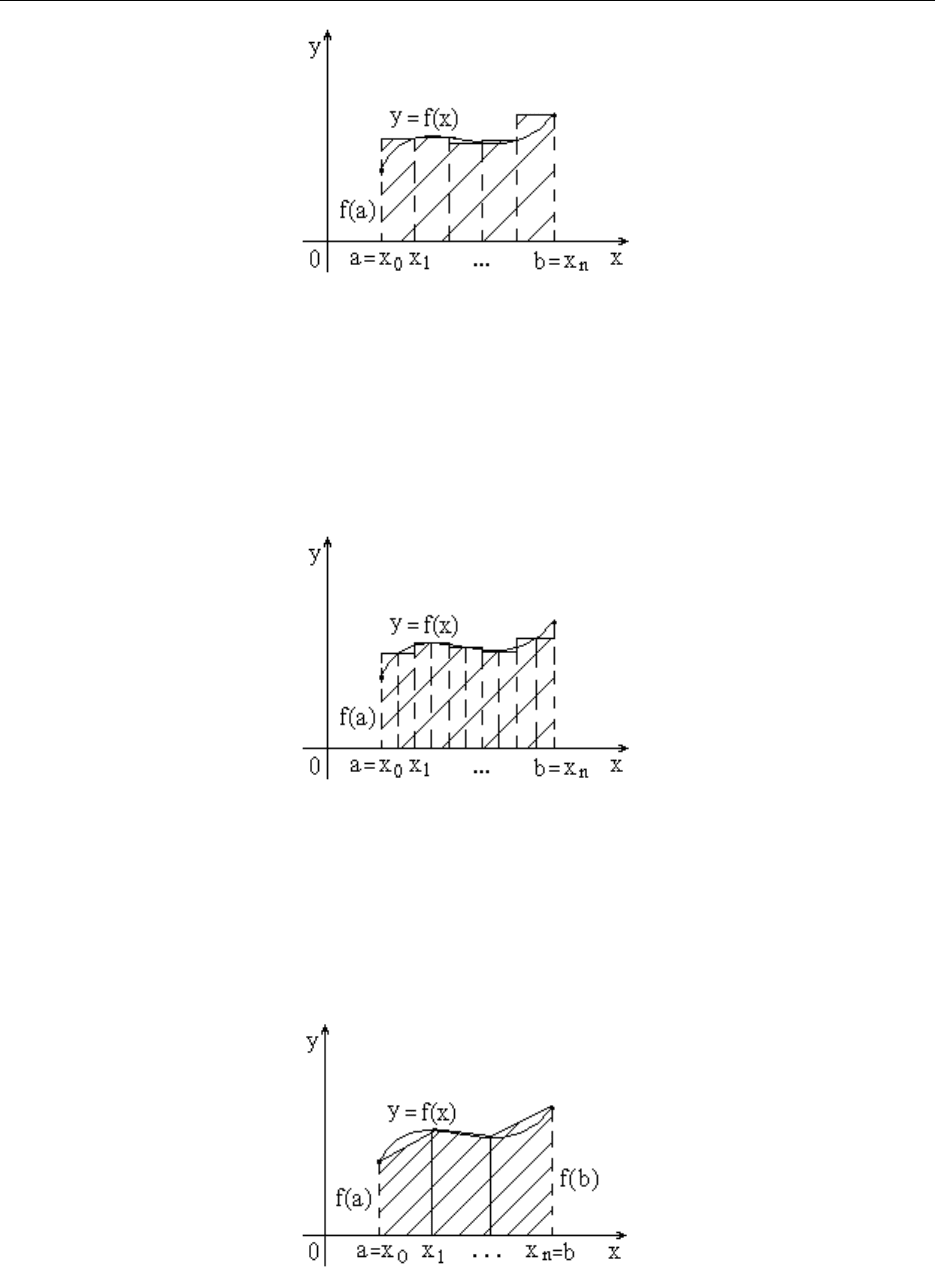
Обобщенная формула правых прямоугольников
Геометрическая иллюстрация
137
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
Введем обозначение :
(13.2)
Обобщенная формула центральных прямоугольников
Геометрическая иллюстрация
Введем обозначение :
(13.3)
Обобщенная формула трапеции
Геометрическая иллюстрация
(13.4)
Обобщенная формула Симпсона
138
