Федченко Г.М. Лекции. Численные методы

Подождите немного. Документ загружается.

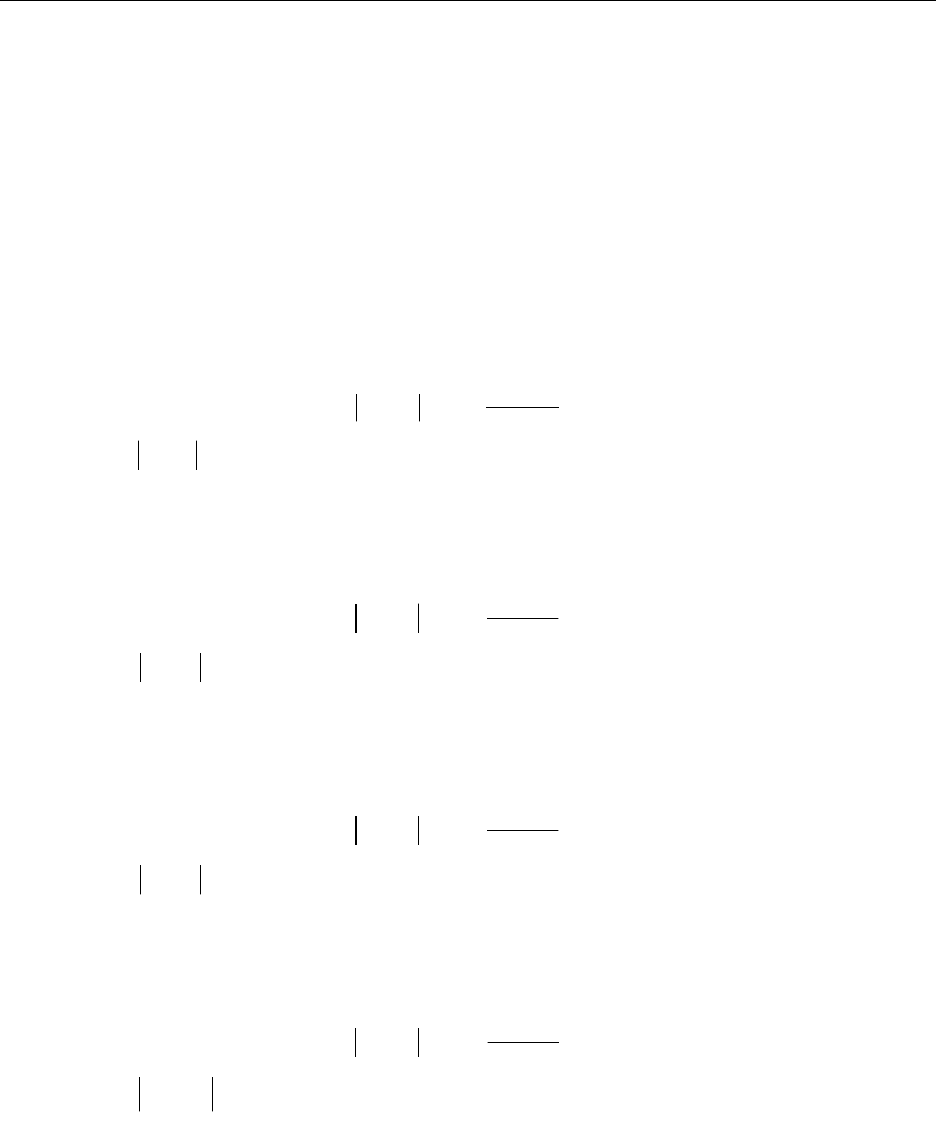
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ

(13.5)

13.6. Оценка погрешности

Если подинтегральная функция f имеет на отрезке [a,b] непрерывную

производную f , то оценка погрешностей формул (13.1) и (13.2) дается

неравенством

 

MJJ





где

 

)(max

xfM





Если подинтегральная функция f имеет на отрезке [a,b] непрерывную

вторую производную f , то оценка погрешностей формулы (13.3) дается

неравенством

 

24n

MJJ





где

 

)(max

xfM





Если подинтегральная функция f имеет на отрезке [a,b] непрерывную

вторую производную f , то оценка погрешностей формулы (4.4) дается

неравенством

 

12n

MJJ





где

 

)(max

xfM





Если подинтегральная функция f имеет на отрезке [a,b] непрерывную

четвертую производную f

, то оценка погрешностей формулы (4.5) дается

неравенством

 

180n

MJJ





где

 

)(max

xfM



Эмпирический критерий оценки точности вычисления интеграла

На практике широко применяется следующий прием, пригодный для

каждого из рассматриваемых методов. Искомый интеграл вычисляется

дважды: при делении отрезка [a,b] на n частей и на 2n частей.

Полученные интегралы J

сравниваются, и совпадающие первые

десятичные знаки считаются верными.

139

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ

13.7. Контрольные вопросы и упражнения

1. Сформулируйте постановку задачи вычисления значения

определенного интеграла и ее геометрический смысл.

2. Сформулируйте общие подходы к решению задачи интегрирования

численными методами.

3. Вычислите приближенно интеграл



dxx

для n=4 по формулам:

a) правых прямоугольников,

b) левых прямоугольников,

c) центральных прямоугольников,

d) трапеций,

e) Симпсона.

Вычислив точное значение интеграла по формуле Ньютона-Лейбница,

оцените абсолютную и относительные погрешности полученных каждым

методом приближенных значений.

4. Убедитесь в том, что формула центральных прямоугольников точна

для многочленов

t,1

, а формула Симпсона – для многочленов

,,,1 ttt

5. Оцените теоретически значение шага интегрирования h для

приближенного вычисления интеграла



)sin( dxx

по формуле Симпсона

с точностью







6. Оцените минимальное число разбиений отрезка интегрирования n для

приближенного вычисления интеграла



)sin( dxx

по формуле трапеций,

обеспечивающее точность







140

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Лекция14

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ

УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА

14.1. Постановка задачи

В классическом анализе разработано немало приемов нахождения

решений дифференциальных уравнений через элементарные (или

специальные) функции. Между тем весьма часто при решении практических

задач эти методы оказываются либо совсем неприменимыми, либо их

решение связывается с недопустимыми затратами усилий и времени.

По этой причине для решения задач практики созданы методы

приближенного решения дифференциальных уравнений. В зависимости от

формы представления решения, эти методы подразделяются на три основные

группы.

1. Аналитические методы, применение которых дает решение

дифференциального уравнения в виде аналитического выражения.

2. Графические методы, дающие приближенное решение в виде графика.

3. Численные методы, когда искомая функция получается в виде таблицы.

Остановимся на численных методах. Решим простейшее

обыкновенное дифференциальное уравнение первого порядка, разрешенное

относительно первой производной

. (14.1)

Общее решение уравнения (14.1) имеет вид

, (14.2)

где С - произвольная постоянная. Геометрически общее решение (14.2)

представляет собой семейство интегральных кривых, т.е. совокупность

линий, соответствующих различным значениям постоянной С.

Интегральные кривые обладают тем свойством, что в каждой точке

М(х,у) наклон касательной удовлетворяет условию

Таким образом, дифференциальное уравнение в разрешенном

относительно производной виде устанавливает явную связь между

141

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

координатами точки М(х,у) и угловым коэффициентом касательной к

интегральной кривой в этой точке.

Если функция определена на некоторой области D плоскости, то

каждой точке соответствует некоторое направление, угловой коэффициент

которого равен . Указывая это направление единичным вектором,

проходящим через точку М, мы получим на D поле направлений.

Интегральные кривые (14.2) суть кривые, для которых упомянутые

направления являются направлениями касательных. Следовательно, с

геометрической точки зрения задача решения дифференциального уравнения

(14.1) заключается в нахождении кривых, направление касательных к

которым в каждой точке совпадает с направлением поля. Конечно, в данном

случае интегральные кривые принадлежат области D.

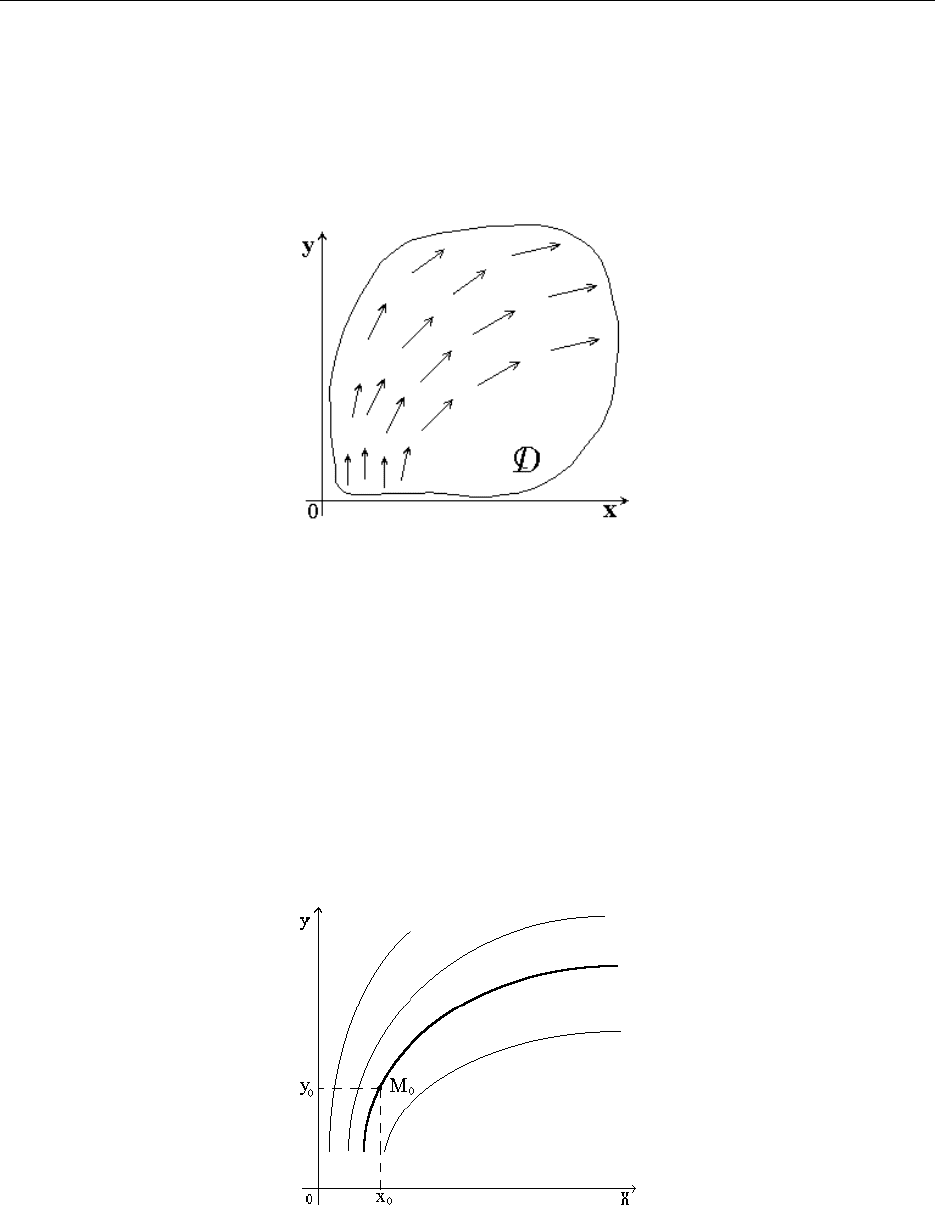
Если задать точку , через которую должна проходить интегральная

кривая, то тем самым из бесконечного семейства интегральных кривых, в

простейшем случае, выделяется некоторая определенная интегральная

кривая, которая соответствует частному решению дифференциального

уравнения (14.1).

Аналитически это требование сводится к так называемому

начальному условию: при .

Задача Коши (начальная задача): найти решение уравнения в виде

функции , удовлетворяющей начальному условию:

, (14.3)

т.е. принимающей при заданное значение .

Геометрически задача Коши формулируется так: найти интегральную кривую дифференциального

142

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

уравнения , проходящую через заданную точку .

Замечание: Дифференциальные уравнения являются математическим

аппаратом, с помощью которого мы можем изучать процессы, протекающие

в природе. Если условия задачи полностью определяют процесс, то он

должен протекать однозначно, т.е. решение дифференциального уравнения,

дающее закон протекания процесса, должно быть единственным. Общее

решение дифференциального уравнения содержит произвольные постоянные

и, следовательно, не дает определенного ответа на поставленный вопрос.

Поэтому при решении конкретных задач, кроме дифференциального

уравнения, нужны еще дополнительные условия. В простейшем случае, это

начальные условия, и мы приходим к задаче Коши.

В курсе математического анализа рассматривалась теорема о

существовании и единственности решения задачи Коши.

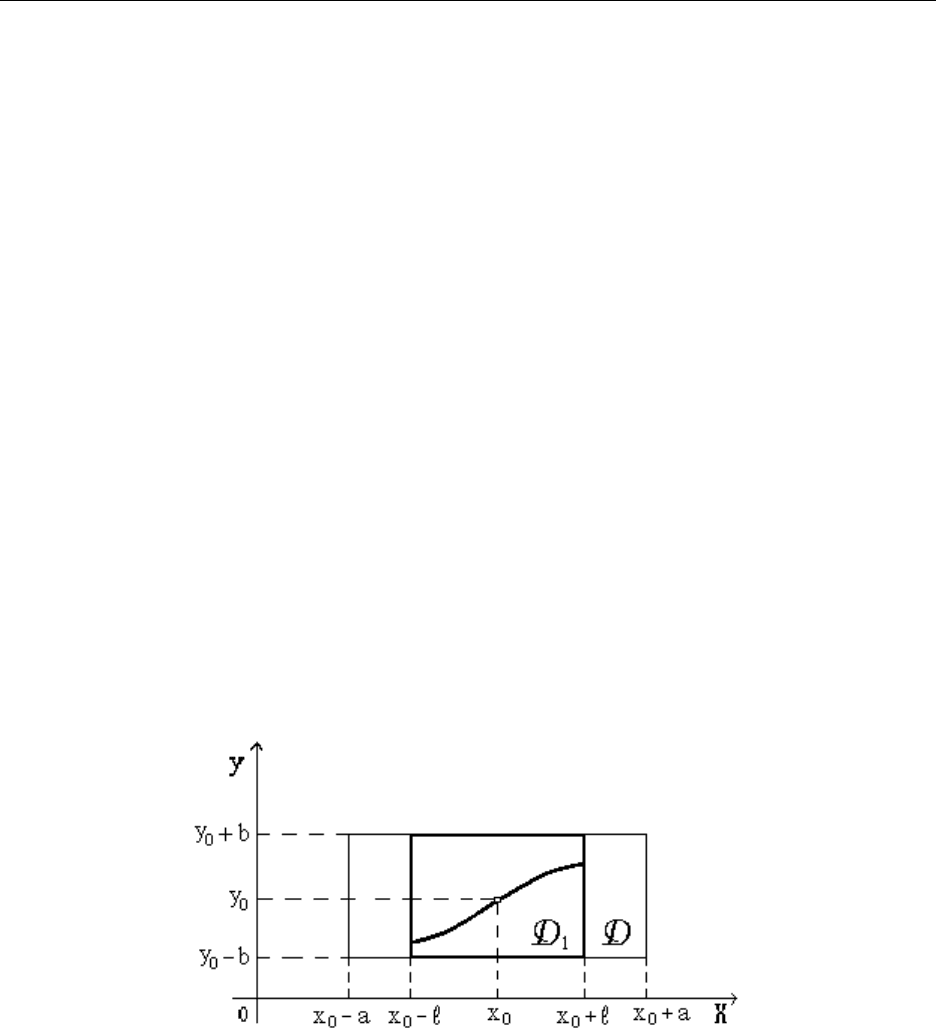
Теорема: Пусть функция определена и непрерывна в области D,

и имеет в ней ограниченную производную , т.е. при .

Тогда на отрезке , где , существует и притом единственное решение

уравнения , удовлетворяющее начальному условию . При этом выполняется

неравенство , при .

На рисунке в плоскости х0у изображен прямоугольник D и

принадлежащий ему прямоугольник

Теорема утверждает, что если на прямоугольнике D функция

непрерывна и имеет ограниченную производную , то через точку проходит

единственная интегральная кривая , определенная для всех значений . Она

полностью принадлежит прямоугольнику D

Подчеркнем, что теорема гарантирует существование определенного

отрезка , на котором заведомо существует и единственно решение

уравнения (1), проходящее через точку . В дальнейшем мы будем искать

приближенное решение именно на этом отрезке, потому что нельзя ручаться,

что указанное решение определено вне L.

143

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

14.2. Метод Эйлера

Классы уравнений, для которых разработаны методы получения

точных решений, сравнительно узки и охватывают только малую часть

возникающих на практике задач. Общего же метода для нахождения точного

решения произвольного дифференциального уравнения первого порядка не

существует. Поэтому важное значение приобретают приближенные методы

решений дифференциальных уравнений. Мы рассмотрим простейший из них,

так называемый метод Эйлера для решения задачи Коши.

Пусть дано уравнение

с начальным условием

Найдем таблицу значений функции на отрезке с шагом

табулирования h. Будем предполагать, что на отрезке , где ищется решение,

выполнены все условия, обеспечивающие существование и единственность

решения задачи Коши. Выбрав достаточно малый шаг h, построим, начиная с

точки , систему равностоящих точек . При достаточно малом h производную

в каждой точке заменим на отношение приращения функции к приращению

аргумента:

Подставим приближенное значение в уравнение (14.1):

Выразим :

Вместе с начальным условием получены расчетные формулы метода

Эйлера для вычисления приближенных значений функции у(х) в точках

(14.4)

Расчетные формулы метода Эйлера (14.4) можно получить и из иных

соображений. Проинтегрируем обе части уравнения (14.1) на отрезке

(14.5)

Вычислим приближенное значение определенного интеграла

по методу левых прямоугольников. Получим, что

Следовательно,

Геометрический смысл метода Эйлера

Пусть на заданном отрезке требуется найти решение

144

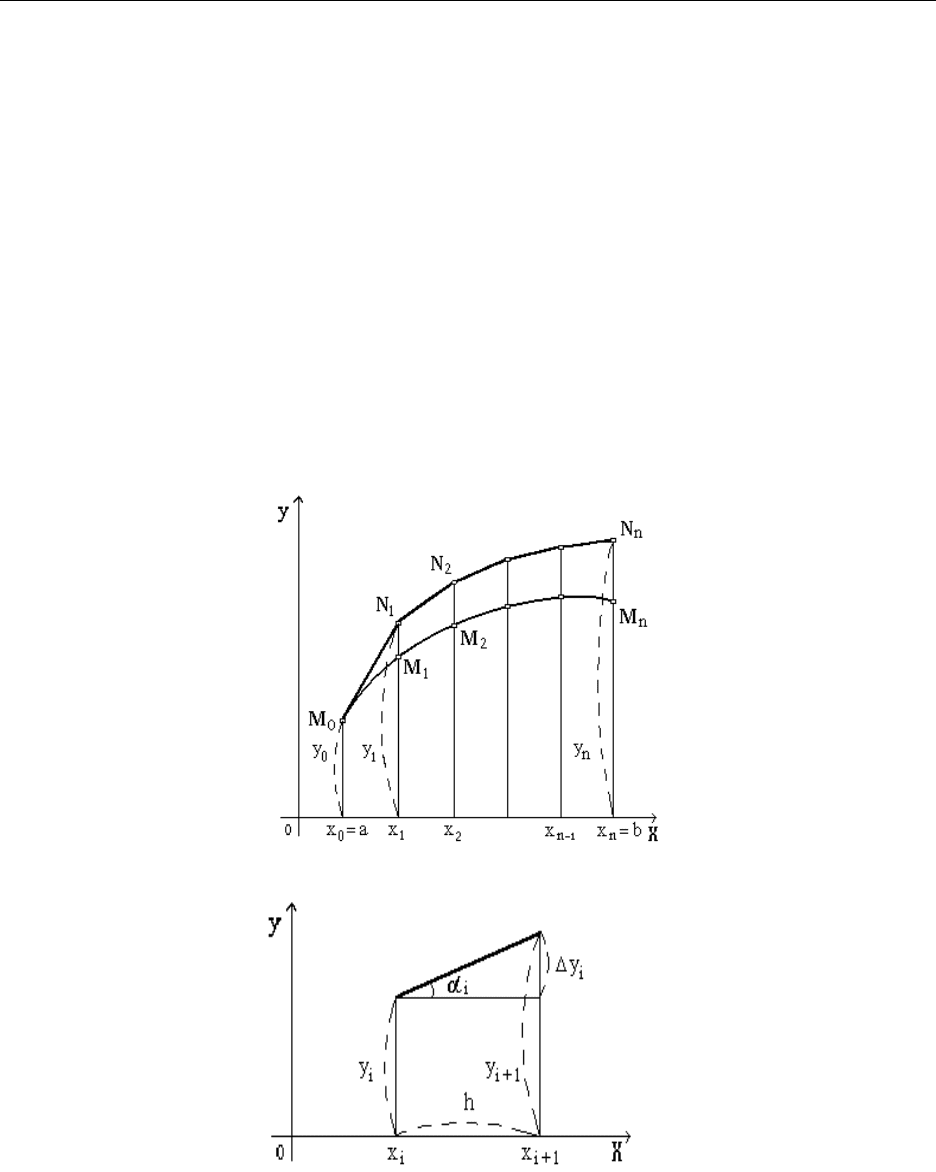
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

дифференциального уравнения первого порядка , удовлетворяющее

начальному условию: .

Геометрически это значит, что для дифференциального уравнения (1)

нужно построить интегральную кривую , проходящую через точку . Из

геометрического смысла производной получаем, что в каждой точке М(х,у)

интегральной кривой ее наклон ( т.е. угловой коэффициент касательной )

удовлетворяет условию

Напомним расчетные формулы метода Эйлера:

Каждое последующее значение функции, начиная с у

, получается

путем добавления к предыдущему значению приращения , зависящее от

наклона интегральной кривой в точке .

Таким образом, по методу Эйлера интегральная кривая M

...M

где заменяется ломаной с вершинами называемой ломаной Эйлера.

Первое звено ломаной касается искомой интегральной кривой в точке . Все

последующие звенья имеют такие же наклоны, что и касательные к

интегральной кривой в точках .

график кусочно-линейной функции у

(x), определяемой на с

145

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

помощью равенств (3) при разбиении отрезка на n частей. Можно доказать

что если существует единственное решение y(x) уравнения (14.1),

удовлетворяющее начальному условию и определенное на отрезке , то

последовательность ломаных Эйлера сходится на к истинному решению

задачи Коши при .

Думаем, что теперь уже очевидна возможность вывода формул метода

Эйлера и из чисто геометрических соображений.

Физический смысл метода Эйлера

С механической точки зрения мы непрерывный процесс,

описываемый дифференциальным уравнением (14.1), заменяем импульсным

процессом, протекающим с постоянной скоростью на элементарных

промежутках , скорость которого меняется скачками при переходе к

последующему промежутку.

Недостатки метода Эйлера:

1) Малая точность при значительном шаге h, большой объем работы при

малом шаге.

2) Систематическое накопление ошибок, т.к. при вычислении значений на

последующих отрезках исходные данные не являются точными и содержат

погрешности, зависящие от неточности предшествующих вычислений.

Оценка точности

Метод Эйлера обладает малой точностью (в пределах одной-двух

значащих цифр), к тому же погрешность каждого шага систематически

возрастает. Наиболее приемлемым для практики методом оценки точности

является способ двойного счета - с шагом h и с шагом . Если -

приближенное значение решения, полученное при расчете с шагом h, -

улучшенное значение, полученное при шаге , и - точное значение решения,

то абсолютную погрешность определяют из приближенного равенства.

Совпадение десятичных знаков в полученных двумя способами

результатах дает естественные основания считать их верными.

14.3. Модифицированный метод Эйлера

Модифицированный метод Эйлера при практически том же объеме

вычислительной работы дает погрешность порядка h

, вместо h в обычном

методе Эйлера, что достигается с помощью очень простого приема.

Возвратимся к формуле (14.5). При получении из нее формулы метода

Доказательство см., например, в книге: Петровский И.Г. Лекции по теории обыкновенных

дифференциальных уравнений.- М.: Наука, 1970.

146

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Эйлера мы полагали подынтегральную функцию постоянной, равной ее

значению в левом конце отрезка . Более точное значение получится, если

при вычислении интеграла применить метод центральных прямоугольников,

полагая равной значению в центральной точке отрезка

Но для вычислений по этой формуле необходимо знать значение . Это

значение можно найти приближенно с помощью обычного метода Эйлера с

шагом .

Таким образом, получим следующую последовательность вычислений

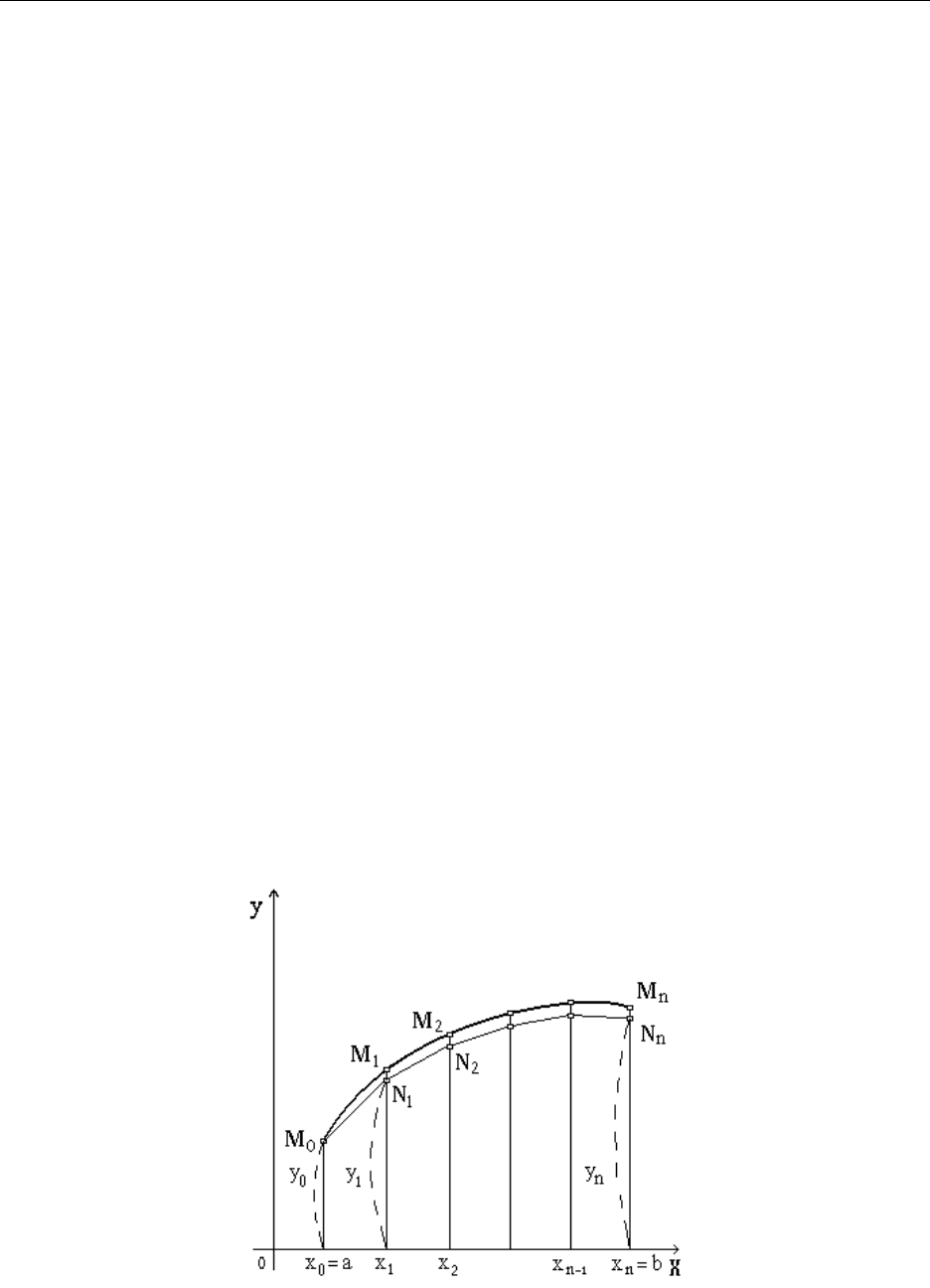
Геометрический смысл модифицированного метода Эйлера

Модификации метода Эйлера применяются для того, чтобы более

точно определить направление перехода из точки в точку .

В модифицированном методе Эйлера сначала делаем половинный шаг

по методу Эйлера, вычисляя промежуточные значения

Затем в найденной средней точке определяем наклон интегральной

кривой

По этому наклону определяем приращение функции на целом шаге

И окончательно

147

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Таким образом, интегральная кривая M

M

, где заменяется

ломаной M

...N

. Каждое звено ломаной на отрезке (i=0,1,…,n–1) имеет

то же направление, что и касательная к интегральной кривой в средней точке

отрезка.

Обосновать модифицированный метод Эйлера можно с помощью

идеи графического построения решения дифференциального уравнения.

Пусть для уравнения с начальным условием выполнены на отрезке

все условия существования и единственности решения. Выберем шаг h для

разбиения отрезка системой точек настолько малым, что для всех х между

значения функции у мало отличались от линейной функции. На каждом

участке интегральная кривая заменяется отрезком прямой линии,

параллельной касательной, проведенной к графику решения задачи Коши в

средней точке отрезка.

14.4. Метод Эйлера-Коши

Другой модификацией метода Эйлера является метод Эйлера-Коши.

Его расчетные формулы легко получить, применив при вычислении

интеграла

в уравнении (14.5) метод трапеций.

148