Эськов В.Д., Каталевская А.В. Теоретические основы электротехники. Часть 2
Подождите немного. Документ загружается.

101
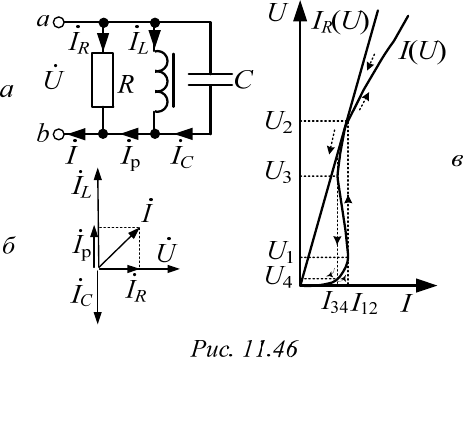
(естественно, при одном напряжении). Кривая I(U) построена на
рис. 11.46, в. Она может быть снята экспериментально только при пита-
нии от источника плавно изменяющегося напряжения. При использова-
нии же источника плавно регулируемого тока наблюдаются скачки
напряжения и «опрокидывание фазы». Так, при плавном увеличении тока
по достижении значения
12
I
происходит скачок напряжения с
1
U
до
2
U
,
дальше ток изменяется плавно. А при плавном уменьшении тока по до-
стижении значения
34
I
происходит скачок напряжения с
3
U
до
4
U
.
Феррорезонанс находит применение в релейных устройствах, кото-
рые используют вышеупомянутые скачки тока или напряжения (релей-
ный или триггерный эффект). Так, например, для защиты нагрузки от
перенапряжений в сети можно подключить к ней параллельно схему
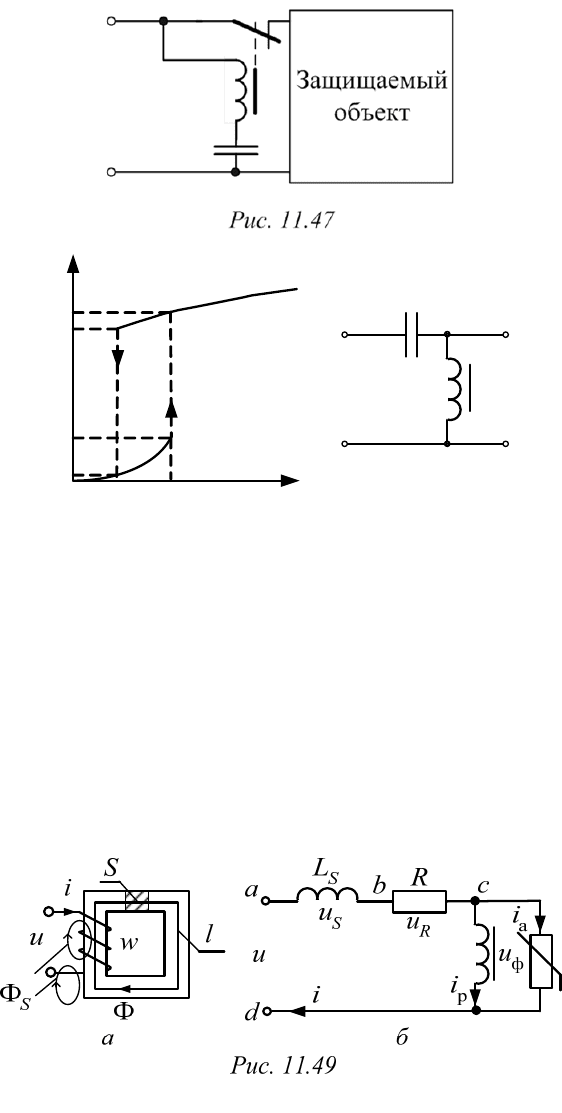
рис. 11.44, а, связанную в свою очередь с реле (рис. 11.47). Тогда при
увеличении напряжения до значений, больших
1
U
, произойдет резкое
увеличение тока. Срабатывание реле от этого тока позволит отключить
нагрузку от сети. Для защиты нагрузки от тока короткого замыкания
можно последовательно с ней включить схему рис. 11.46, а. Если ток в
этой схеме превысит значение
12
,
I
ее полное сопротивление резко воз-
растет и ограничит ток.
Феррорезонансная цепь может быть использована и в стабилизаторах
напряжения. Покажем это с помощью зависимости
(),
L
UI
изображенной на
рис. 11.48, а, которая может быть построена по графикам рис. 11.43 и 11.44.
При работе в области напряжений, превышающих
12
,U
существенное изме-
нение напряжения на входе последовательной цепи приводит к незначитель-
ному изменению напряжения на катушке с ферромагнитным сердечником.
Поэтому, подключив параллельно катушке нагрузку (рис. 11.48, б), можно
обеспечить стабилизацию нагрузочного напряжения.
102
а б
Рис. 11.48
U
12
U
34
U
L4
U
L3
U
L2
U
L1
U
L
(U)
U
L
U
0
U
U
L
11.5.7. Векторная диаграмма и схема замещения
катушки с ферромагнитным сердечником
Воспользуемся методом эквивалентных синусоид, чтобы учесть ре-
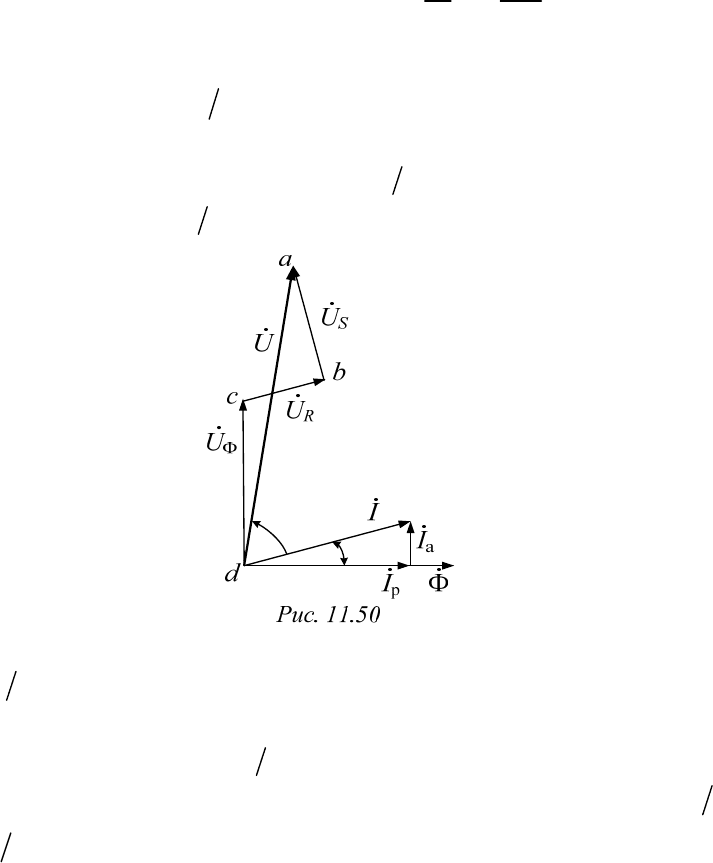
альные свойства катушки со сталью (рис. 11.49, а): потери в стали и ме-
ди, потоки рассеяния, при этом петлю гистерезиса заменим эллипсом
равной площади. Схему замещения, учитывающую вышеперечисленные
свойства, можно представить в виде, показанном на
рис. 11.49, б.
Потоки рассеяния, которые замыкаются вне сердечника, пропорци-
ональны току:
Ф , где
ss s
Li L
индуктивность рассеяния. Линейное
сопротивление R – это активное сопротивление обмотки. Оно учитывает
«потери в меди». Нелинейное сопротивление, параллельное нелинейной
индуктивности, учитывает потери на гистерезис и вихревые токи. Токи
в обоих нелинейных элементах определяются величиной магнитного
потока в сердечнике.
103
Будем считать, что этот поток изменяется по синусоидальному за-
кону:
Ф() Ф (sin ).
m
tt
Тогда мгновенное значение напряжения скла-
дывается из трех составляющих:
.
S
di d
uiRL w
dt dt
В комплексной форме:
ФФ
j,
RS S
UU U U RI LIU
где
Ф
j, 1,414.
m
Uw
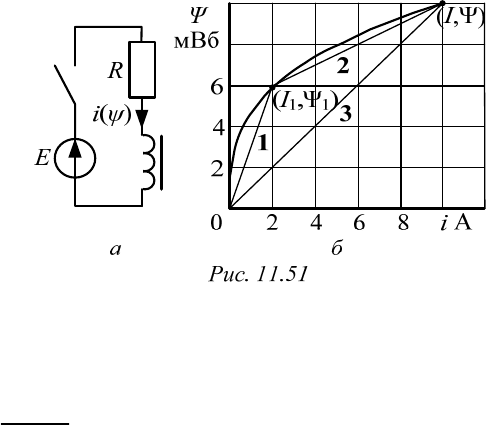
Если построение векторной диаграммы начать с магнитного потока
(рис. 11.50), то
Ф
U
опережает его на
2.
Однако ток отстает от по-
следнего менее, чем на
2,
опережая поток на угол потерь
.
В справочниках в зависимости от амплитуды магнитной индукции
mm
BS
приводятся значения удельных (на единицу массы G) по-
терь в стали
0
()
m
P
B
и намагничивающей мощности
0
()
m
QB
для
определенной частоты
2.f
Затем при известной массе сердеч-
ника можно подсчитать
СТ 0 СТ 0
,,PPGQQG
а затем
рСТФ
,IQU
аСТФ
,
I
PU
ар
j
I
II
и построить их на диаграмме. Наконец, по
известному току вычислим
R
URI
(вектор параллелен I
) и
j
SS
ULI
(вектор перпендикулярен
),I
дополним ими диаграмму,
найдем U и
. Таким образом, будут получены точки
() и ()UI I
на
вольт- и фазо-амперной характеристиках реальной катушки соответ-
ственно. Задаваясь значениями амплитуды магнитного потока в пред-
полагаемом диапазоне изменений и повторяя вышеописанные дей-
ствия, можно построить характеристики полностью и использовать их
в расчетах.
104
11.6. Переходные процессы в нелинейных цепях
11.6.1. Принципиальное отличие переходных процессов
в нелинейных цепях от переходных процессов
в линейных цепях
Переходные процессы в нелинейных цепях существенно отличают-
ся от переходных процессов в линейных цепях.
Нелинейность характеристики даже одного элемента может приве-
сти не только к количественным, но и к качественным изменениям ха-
рактера процесса. Количественные изменения сводятся к тому, что про-
цесс протекает с переменной скоростью, причем по сравнению с уста
-
новившимся режимом могут резко возрасти максимальные значения то-
ков и напряжений. А среди качественных изменений можно отметить
явления, принципиально невозможные в линейных цепях, где процесс
затухает к установившемуся режиму, характер которого обусловлен ха-
рактером источников. В нелинейных цепях возможны колебания с ча-
стотой, отличной от частоты источников, – автоколебания. Процесс мо-
жет оказаться при определенных условиях нарастающим, что заканчи-
вается аварией. Возникают проблемы устойчивости режима и т. д.
Не существует общих методов расчета переходных процессов в не-
линейных цепях. Мы рассмотрим наиболее употребительные и простые
на примере цепи, состоящей из линейного сопротивления R и нелиней-
ной катушки с вебер-амперной характеристикой
,i
которая подклю-
чается к источнику постоянной ЭДС Е (рис. 11.51, а).
Пример 11.13
Дано:
100 В,E
10 Ом,R
ВбАХ за-
дана на рис. 11.51, б
кривой
.i
Найти i(t).
Решение
Состояние послекоммутационной цепи описывается нелинейным
дифференциальным уравнением первого порядка:
()
.
di
R
iE
dt
(11.22)

105
Независимые начальные условия – нулевые (ни ток, ни потокос-
цепление в момент коммутации скачком измениться не могут):
(0) 0, (0) 0.i
Со временем переходный процесс приведет к установившемуся
режиму с постоянным током
( ) 100 10 10 AiIER
и соответ-
ствующим значением потокосцепления
() () 10мВб.I
Рас-
смотрим несколько методов определения i(t) и сравним результаты.
11.6.2. Метод условной линеаризации
Сущность метода заключается в том, что часть характеристики не-
линейного элемента между точками, соответствующими началу
(0)t
и
концу
()t
переходного процесса, заменяется отрезком прямой. Не-
линейный элемент заменяется линейным, чей параметр считается рав-
ным условному дифференциальному параметру нелинейного элемента,
который, в свою очередь, определяется по наклону этого отрезка. Нели-
нейное дифференциальное уравнение переходит в линейное, которое
решается известными методами (например, классическим). Полученное
решение затем можно уточнить с помощью исходной
нелинейной ха-
рактеристики. Метод прост, но неточен, особенно если линеаризующий
отрезок значительно отдаляется от реальной характеристики.
Соединив на рис. 11.51, б отрезком прямой (
3) начало координат
(0)t
с точкой
,,I
соответствующей
,t
получим линеаризо-
ванный рабочий участок характеристики катушки, для которого услов-
ная дифференциальная индуктивность равна
д
1 мГн.LI
Если в дифференциальном уравнении (11.22) заменить
д
,Li
то
оно станет линейным:
д
di
L
Ri E
dt
(11.23)
и его решение, как и в примере 10.4, будет иметь вид:
10000
д
() (1 ) 10 (1 ) А, где 0,1 мс.
tt
it I e e L R
Ему соответствует экспоненциальная кривая
2 на рис. 11.52.
Если в том же уравнении произвести замену
д
,iL
то решение
линейного уравнения
д
dR
E
dt L
будет аналогичным:
10000
() (1 ) 10 (1 ) мВб.
tt
te e

106
Задаваясь значениями t = 0; 0,5
;
; 1,5
; …, подсчитаем
(),t
затем
по ВбАХ найдем соответствующие значения
()i
и построим
()it
кривую
1 на рис. 11.52. Она проходит гораздо ниже кривой 2, так как
реальная ВбАХ обращена выпуклостью к оси
.
11.6.3. Метод кусочно-линейной аппроксимации
Его смысл в том, что рабочий участок характеристики нелинейного
элемента заменяется ломаной линией, для каждого отрезка которой
определяется свой условный дифференциальный параметр. Уравне-
ние (11.22) с использованием этого параметра переходит в линейное и
может быть решено известными методами. Постоянные интегрирования
в решении находятся из условия непрерывности искомой величины на
границах участков (припасовывание
решений). Метод более точен, чем
предыдущий, особенно при увеличении количества отрезков ломаной
линии, но и, соответственно, более громоздок.
На рис. 11.51, б точку с координатами
1
2I
А,
1
6
мВб соеди-
ним с началом координат и с точкой [I,
], заменив тем самым реаль-
ную кривую
(i) двумя отрезками ломаной. Для первого из них (1)
1
L
i
, где
11
1
62 3LI
мГн, тогда
11
310 0,3LR
мс.
Для второго (
2)
12 1
(),
L
iI
где
21
1
()()480,5мГн,LII
при этом
22
0,5 10 0,05 мс.LR
Соответствующие решения линеаризованного уравнения:
1
11
() (1 ) при ,
t
it I e t t
1
2
21 1
() ( ) при ,
tt
it I I Ie t t
где момент перехода рабочей точки с одного отрезка ломаной на другой
11 1
ln(1 ) 0,3ln(1 2 10) 0,09 мс.tII
По этим формулам построена кри-
вая с изломом
3 на рис. 11.52. Она
проходит выше кривой
2 и пересекает
кривую
1 (что неудивительно, так как
и значит
A
t
1
2
2
4
6
8
0
3
4
0,20,1 0,3 0,4
i
мс
Рис. 11.52
1 д 2
L
LL
12
).
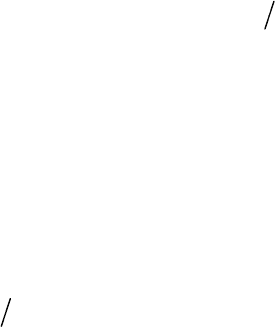
107
11.6.4. Метод последовательных интервалов времени
Суть этого метода в том, что время переходного процесса разбива-
ется на небольшие (обычно равные) промежутки времени, в течение
каждого из которых условный дифференциальный параметр нелинейно-
го элемента считается неизменным. Дифференциальное уравнение при
этом переходит в разностное (уравнение в конечных приращениях) [9],
что позволяет находить значение искомой величины в конце каждого
интервала
по ее значению в начале этого интервала.
Метод хорошо алгоритмизируется, что дает возможность исполь-
зовать в расчетах стандартные программы для ЭВМ по методам Эйлера,
Рунге–Кутта и др. При выборе достаточно малой длительности каждого
интервала обеспечивается высокая точность расчета.
В рассматриваемом примере уравнение в конечных приращениях
имеет вид:
.tRiE
На k-м интервале
()
k
tkt
приращение потокосцепления
k
определяется током
k
i
в начале этого интервала, который в свою оче-
редь находится по ВбАХ для уже известного значения
.
k
По методу Эйлера
().
kk
E
iR t
Затем подсчитываются
1kkk
в момент времени
1
(1)
k
tkt
и
11
()
kk
ii
и т. д.
Выбор шага по времени
t диктуется точностью расчета. Она ока-
жется вполне удовлетворительной для графических построений при
5,t
где
определяется методом условной линеаризации.
Примем
t = 0,01 мс. Первые циклы расчета таковы:
k = 0; t = 0;
0
0;
0
0i
;
00 0
0; 0; 0; 0; 100 0,01 1 мВб;kt i
11
1; 0, 0 1 мс;1мВб;0,3A;kt i
1
0,3i
А;
1
(100 0,3 10) 0,01 0,97 мВб;
22
2; 0,02 мс; 1 0,97 1,97 мВб;0,7Akt i
и т. д.
Вычисления продолжаются до тех пор, пока не окажется
n
iI
с
заданной точностью.
В данном примере вполне достаточно получить значение
9,99 A
n
i
при
30,n
что соответствует моменту времени
0,3 мс.t
По результатам расчета на рис. 11.52 построена плавная кривая
4. Она
близка к кривой
3, но вычисления гораздо более просты, да и те могут
быть поручены ЭВМ.
Если сравнить все четыре кривые между собой, то можно отметить
следующее. Во-первых, наиболее точным является метод последова-

108
тельных интервалов времени при выборе достаточно малого шага по
времени. Во-вторых, метод кусочно-линейной аппроксимации тоже
весьма точен. Ведь даже при минимальном числе отрезков ломаной
кривая
3 близка к кривой 4. Наконец, кривые 1 и 2 тем больше отлича-
ются от кривой
4, чем дальше отрезок прямой 3 на рис. 11.51, б отходит
от реальной ВбАХ. Поэтому метод условной линеаризации есть смысл
применять для оценки реальной длительности переходного процесса
(3)
и последующего выбора шага по времени при использовании ме-
тода последовательных интервалов времени.
11.6.5. Особенности применения метода переменных состояния
к расчету переходных процессов в нелинейных цепях
Если цепь линейная, то коэффициенты, входящие в уравнения со-
стояния, – постоянные величины, выражающиеся через параметры пас-
сивной части цепи. Если нелинейная, то в уравнения входят также ана-
литические выражения или функциональные зависимости, описываю-
щие характеристики нелинейных элементов.
При наличии в цепи нелинейной индуктивности в качестве одной
из переменных состояния следует выбрать
ее потокосцепление, так как
именно его производная
L
d
u
dt
– напряжение на катушке – входит в
уравнения второго закона Кирхгофа, а ток будет представлен в уравне-
ниях вебер-амперной характеристикой
().
L
i
Соответствовать нелинейному конденсатору в числе переменных со-
стояния должен его заряд, поскольку именно его производная
C
i
dt
dq
– ток
конденсатора – входит в уравнения первого закона Кирхгофа, а его напряже-
ние будет фигурировать в виде кулон-вольтной характеристики
().
C
uq
Когда в цепи есть нелинейное сопротивление, то переменной со-
стояния будет либо ток линейной индуктивности, если она включена
последовательно с сопротивлением, либо напряжение на линейной ем-
кости, если последняя включена параллельно этому сопротивлению.
Вольтамперная характеристика введет вторую величину в уравнения
как функцию переменной состояния. В иных случаях и комбинация
ВАХ
с переменными состояния окажется более сложной.
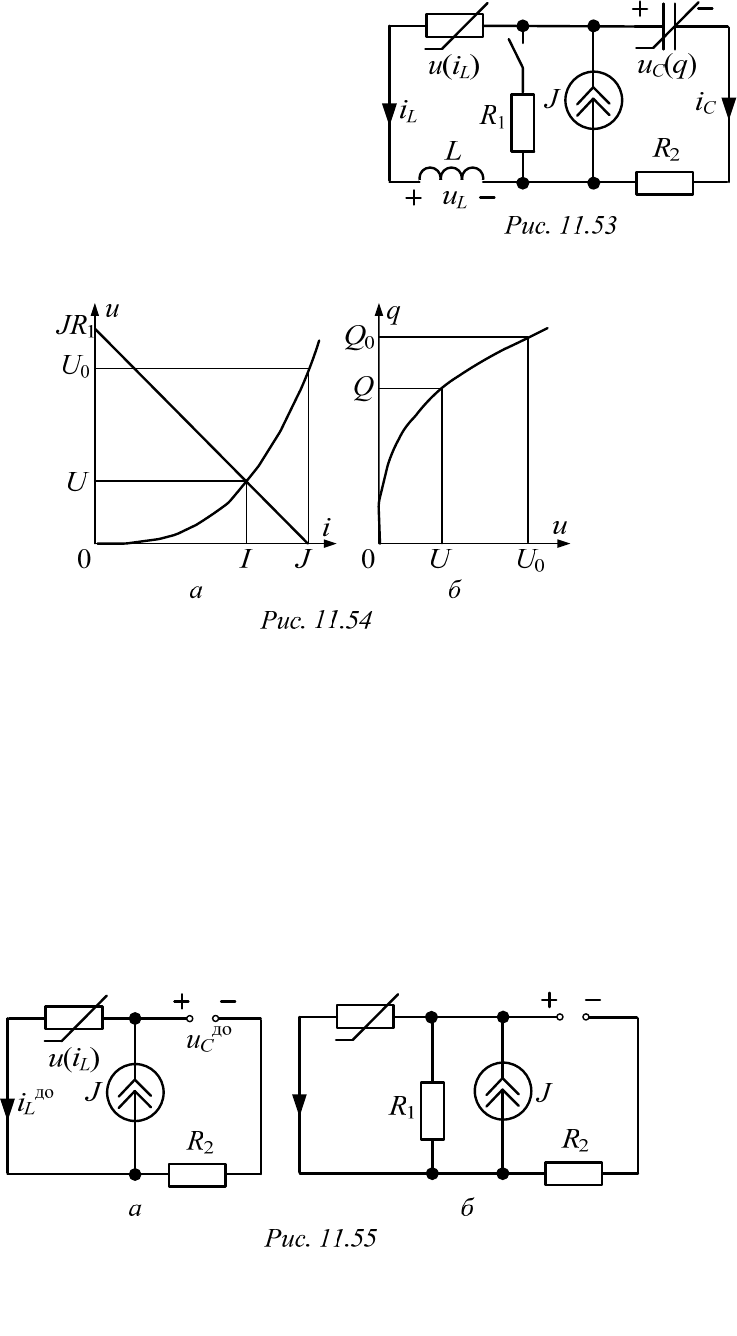
В качестве примера составления уравнений состояния в цепи вто-
рого порядка с двумя нелинейными элементами рассмотрим схему,
приведенную на рис. 11.53. Заодно наметим и порядок расчета методом
переменных состояния.
109
Пример 11.14
Известны ток источника
const
J
, сопротивления
1
R
и
2
R
,
индуктивность L, а также ВАХ
()
L
ui
и КлВХ
()
C
uq
, которые показаны на
р
ис. 11.54, а и б.
Найти
() ().
L
C
it и ut
Решение
1. Расчет докоммутационной цепи в установившемся
режиме и
определение независимых начальных условий по законам коммутации.
В схеме действует источник постоянного тока, поэтому в устано-
вившемся режиме катушка представляет собой закоротку, а конденса-
тор – разрыв цепи (рис. 11.55, а). Поэтому
до
(0),
L
L
iJi
по ВАХ
0
() (0).
C
uJ U u
Затем по КлВХ найдем
00
() (0).qU Q q
2. Расчет послекоммутационной цепи в установившемся режиме
по схеме рис. 11.55, б.
()
L
i
()
C
u
()u

110
Параллельно включенные J и
1
R
по отношению к зажимам нели-
нейного сопротивления представляют известную схему эквивалентного
генератора с током короткого замыкания J и напряжением холостого
хода
1
JR
. Его внешняя характеристика – прямая на рис. 11.54, б, а ее
точка пересечения с ВАХ нелинейного сопротивления позволяет найти
() , () () .
L
C
iIuuU
После этого по КлВХ конденсатора найдем
() () .qqUQ
3. Выбор переменных состояния.
Очевидно, это
и ,
L
qi
так как их производные
C
i
dt
dq
и
L
u
dt
di
LL
легко выражаются через
,,(), ()
L
LC
iJui uq
по законам
Кирхгофа.
4. Уравнения состояния. Будем искать их в виде:
111 1 1
222 2 2
() ( );
() ( ).
LL
CC
LL
L
L
C
dq
iAJBqCiDuqEui
dt
udi
A
JBqCi Duq Eui
Ldt
(11.24)
Заменим (рис. 11.56, а), в соответствии с теоремой компенсации,
катушку источником тока
,
L
i
направленного так же, как и в исходной
схеме, конденсатор – источником ЭДС
C
u
c такой же полярностью, как
у напряжения в той же схеме. Затем воспользуемся принципом наложе-
ния для определения составляющих тока в конденсаторе
C
i
и напряже-
ния на катушке
,
L
u
оставляя в каждой подсхеме по одному источнику:
123
123
;
.
CC C C
L
L
LL
ii i i
uu u u
(11.25)
В подсхеме с источником тока J (второй источник тока отключен,
вместо источника ЭДС стоит закоротка – рис. 11.56, б) имеем:
112
11
12 12
и .
CL
JR JR R
iu
R
RRR
В подсхеме с источником тока
L
i
(рис. 11.5, в)
112
22
12 12
и ().
LL
CLL
iR iRR
iuui
RR RR
Наконец, в подсхеме с источником ЭДС
C
u
(рис. 11.56, г)
1
33
12 12
() ()
и .
CC
CL
uq uqR
iu
R
RRR
