Эськов В.Д., Каталевская А.В. Теоретические основы электротехники. Часть 2
Подождите немного. Документ загружается.


91
Обмотки с числом витков
2
w
также включены последовательно, но
на левом сердечнике согласно, а на правом – встречно по отношению к
обмоткам с числом витков
1
.w
В этом случае напряжение
dt
d
w
dt
d
w
dt
d
wuuu
ВАВА
2
242022222
2...)(2)(
не содержит нечетных гармоник и постоянной
0
0.
d
dt
Основной при этом оказывается гармоника второго порядка, часто-
та которой вдвое больше частоты тока
1
i
.
11.5.3.3. Магнитный усилитель
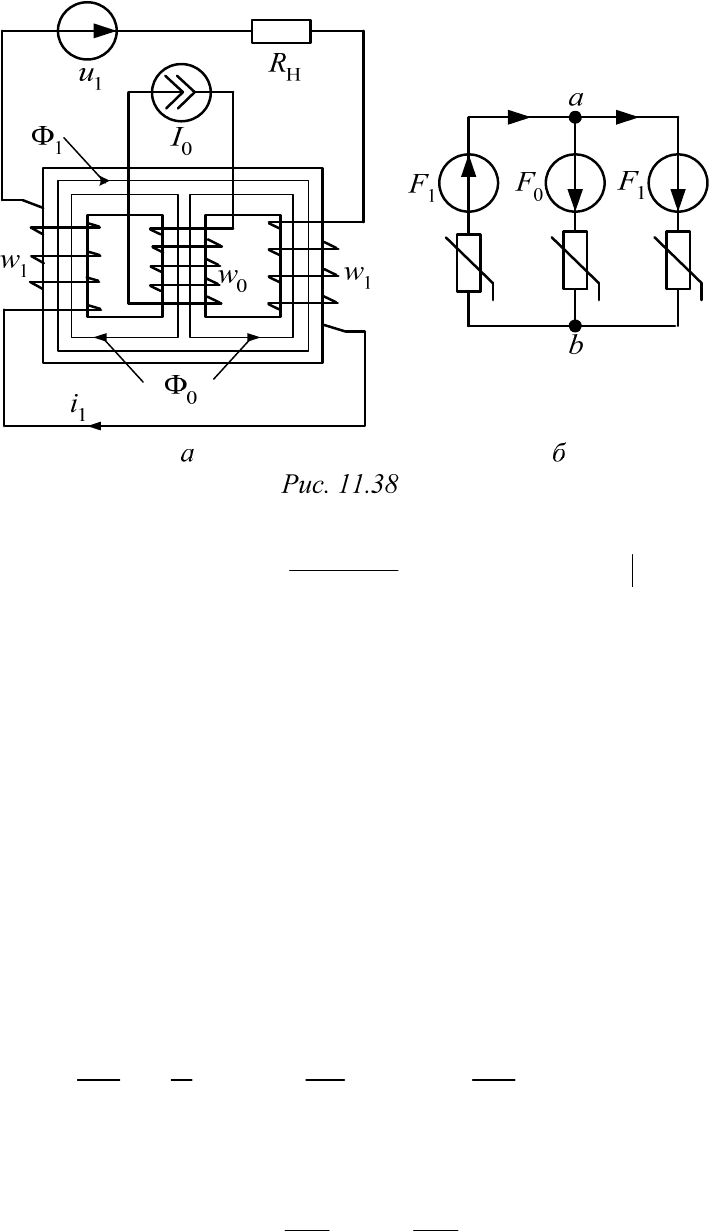
На рис. 11.38, а показана схема так называемого усилителя мощно-
сти с последовательным соединением обмоток переменного тока, а на
рис. 11.38, б – схема замещения его магнитной цепи. В левом стержне
постоянный и переменный магнитный потоки имеют одинаковые поло-
жительные направления, а в правом – противоположные. Принцип дей-
ствия усилителя тот же, что и у
катушки с подмагничиванием, рассмот-
ренной в примере 11.11. За счет изменения малого постоянного тока
0
I
в обмотке с большим числом витков
0
w
можно управлять большим пе-
ременным
1
i
(без изменения амплитуды напряжения
1
() sin( )
m
ut U t
и
сопротивления
Н
),R
а значит, и мощностью нагрузки
2
Н 1 Н
P
IR
(отсю-
да и название усилителя).
Переменный магнитный поток замыкается по внешнему контуру
магнитной цепи, поэтому цепь постоянного тока не нужно защищать от
действия больших переменных ЭДС, которые наводились этим потоком
в обмотке с числом витков
0
w
в вышеуказанном примере. В данном
случае и ток, и магнитный поток несинусоидальны. В силу симметрии
ВбАХ сердечника четные гармоники тока в обмотках
1
w
должны были
бы иметь разные знаки, но это невозможно, поскольку эти обмотки со-
единены последовательно и в них протекает один и тот же ток. Поэтому
переменный ток
1
i
содержит только нечетные гармоники.
92
10
10
Эффективность работы устройства оценивается коэффициентом
усиления по мощности
0
HH0
H0 H
0
0
. Здесь
P
I
PP
kPP
P
мощ-
ность нагрузки при отсутствии тока управления, а
000
PIU
мощ-
ность цепи управления.
11.5.4. Электрические цепи с вентилями
Нелинейные сопротивления с несимметричной ВАХ широко при-
меняются для преобразования переменного тока в постоянный. Такие
нелинейные элементы, обладающие односторонней проводимостью,
называются выпрямителями или электрическими вентилями.
Схема однополупериодного выпрямления переменного тока была
рассмотрена в примере 11.12. В ней использовался лишь один вентиль,
который в течение одного полупериода пропускал ток в нагрузку, а во
время второго был заперт. Разложение напряжения на нагрузке в ряд
Фурье в этом случае выглядит так:
22
( ) 1 cos( ) cos(2 ) cos(4 ) ...
213 35
m
U
ut iR t t t
(11.18а)
Здесь
НД
,RR R
.
mm
UE
Постоянная составляющая и дей-
ствующее значение напряжения в этой схеме равны:
.
2
,
0
mm
U
U
U
U
(11.18б)
93
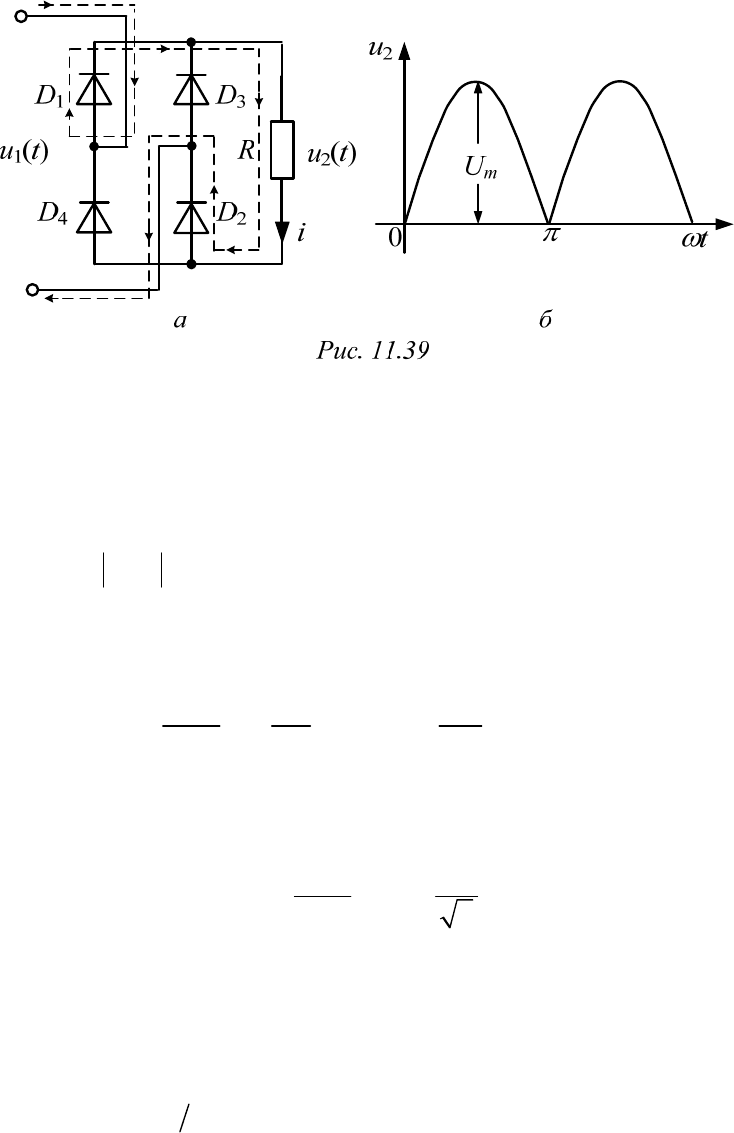
Схема двухполупериодного выпрямления (мостовая) приведена на
рис. 11.39, а. При изменении полярности приложенного напряжения ток
течет разными путями, но через нагрузку всегда в одном направлении.
Здесь пунктиром показан путь тока при положительной полярности
напряжения
1
() sin( ),
m
ut U t
когда открыты диоды
1
иD
2
,D
а
3
иD
4
D
заперты. При отрицательной полярности этого напряжения
откроются диоды
3
иD
4
D
, а
1
иD
2
D
будут заперты. В обе полови-
ны периода ток в сопротивлении R течет сверху вниз. Поэтому зависи-
мость
)()(
12
tutu
имеет вид, показанный на рис. 11.39, б. В разложе-
нии этой кривой по сравнению с напряжением однополупериодного вы-
прямления (11.18а) исчезает первая гармоника, а остальные слагаемые
удваиваются:
2
2
22
( ) 1 cos(2 ) cos(4 ) ...
13 35
m
U
ut t t
(11.19а)
Поэтому в данной схеме постоянная составляющая выходного
напряжения возрастает вдвое, а его действующее значение становится
таким же, как у входного напряжения:
0
2
,.
2
mm
UU
UU
(11.19б)
Трехфазная схема выпрямления с нагрузкой в нулевом проводе
показана на рис. 11.40, а. В ней диоды работают поочередно. Открыт
диод только в той фазе, напряжение на которой при положительной по-
лярности окажется в данный момент больше, чем на другой фазе. Если
система фазных напряжений симметрична, причем
cos( ),
A
m
uU t
то в
интервале
03t
открыт диод в фазе А, затем на протяжении трети
периода – диод в фазе В и так далее. Ток в любом случае замыкается по
нулевому проводу в одном направлении. На рис. 11.40, в утолщенная
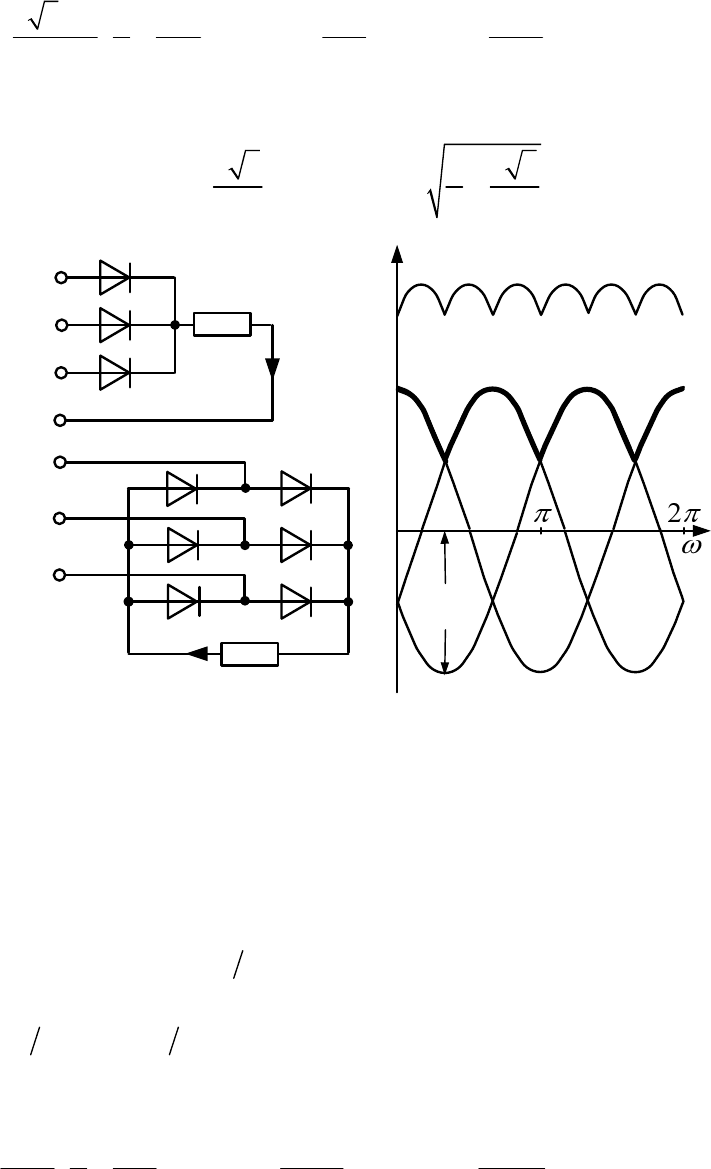
94
кривая напряжения на нагрузке
()ut
огибает кривые фазных напряже-
ний в верхней полуплоскости. Разложение этой кривой в ряд Фурье
имеет вид:
33
11 1 1
( ) cos(3 ) cos(6 ) cos(9 ) ...
224 57 810
m
U
ut t t t
(11.20а)
Постоянная составляющая и действующее значение напряжения
увеличиваются по сравнению с предыдущей схемой:
0
33 1 33
,.
224
mm
UUUU
(11.20б)
Рис. 11.40
u(t)
i
A
B
C
N
R
u(t)
i
A
B
C
R
а
б
u
0
t
U
m
AC AB
u
A
u
B
u
C
BC
CA
CB
BA
в
Схема Ларионова (трехфазная мостовая) показана на рис. 11.40, б. В
этой схеме каждую шестую часть периода открыта лишь та пара диодов, к
которой приложено в данный момент наибольшее линейное (междуфаз-
ное) напряжение положительной полярности. Естественно, возрастают по-
стоянная составляющая и действующее значение напряжения на выходе
выпрямителя. При тех же фазных напряжениях, что и
в предыдущей схе-
ме, в интервале
03t
открыт правый диод фазы А и левый – фазы
С, так что нагрузка находится под напряжением
() ().
A
C
ut u t
В проме-
жутке
323t
действует линейное напряжение
(),
B
C
ut
затем
()
B
A
ut
и так далее. Соответствующая кривая напряжения на нагрузке
также показана на рис. 11.40, в, ее разложение в ряд Фурье:
3
12 2 2
( ) cos(6 ) cos(12 ) cos(18 ) ...
257 1113 1719
m
U
ut t t t
(11.21а)
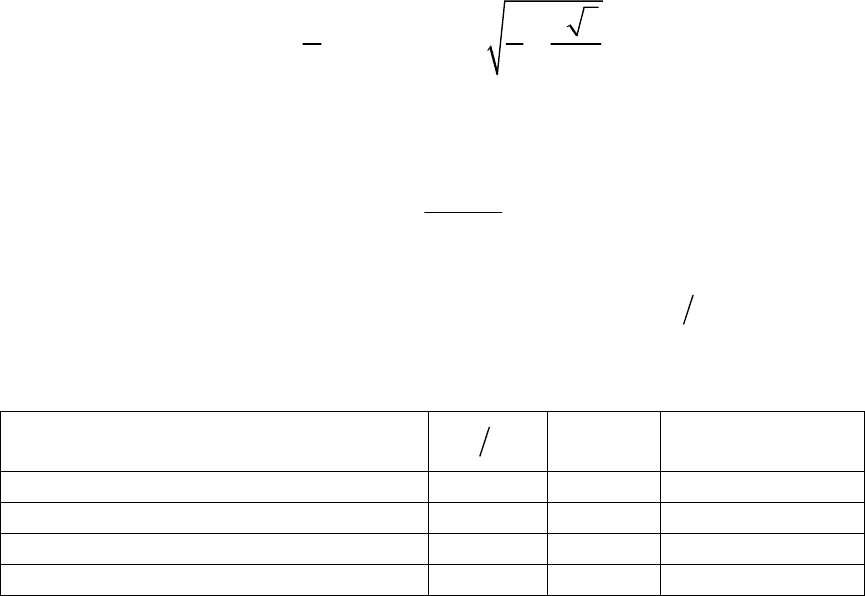
95
Максимумы кривой равны амплитуде линейного напряжения, а
наименьшие значения превышают амплитуду фазного в полтора раза.
При этом ток в нагрузке течет в одном и том же направлении, а посто-
янная составляющая и действующее значение напряжения u(t) становят-
ся почти равными друг другу:
0
3393
,
24
mm
UUUU
. (11.21б)
Качество выпрямления оценивают коэффициентом пульсации, ко-
торый определяется как отношение амплитуды основной гармоники
выпрямленного напряжения к его постоянной составляющей
осн
П
0
.
m
U
k
U
Разумеется, чем меньше
П
,k
тем ближе выпрямленное напряжение
к постоянному. Для сравнения значения отношения
0 m
UU
и коэффи-
циента пульсации в различных схемах приведены в табл. 11.4.
Таблица 11.4
Схема выпрямления
0 m
UU
П
k
Расчетные
формулы
Однополупериодная 0,318 1,57 (11.18a)
Двухполупериодная мостовая 0,636 0,67 (11.19a)
Трехфазная с нулевым проводом 0,828 0,25 (11.20a)
Трехфазная мостовая Ларионова 1,656 0,057 (11.21a)
Отсюда видно, что наименьшие пульсации при наибольшей вели-
чине постоянной составляющей обеспечивает схема Ларионова. Но и в
других схемах результат выпрямления можно улучшить за счет приме-
нения электрических фильтров, даже самых простых (например, вклю-
чить параллельно нагрузке конденсатор или последовательно с ней ка-
тушку индуктивности).
11.5.5. Расчет нелинейных цепей по характеристикам
для действующих значений (метод эквивалентных синусоид)
Значительную часть расчета сложной цепи обычно занимают
упрощающие ее преобразования. Если цепь состоит из инерционных
элементов, то при синусоидальных ЭДС или токах источников синусои-
дальны и остальные токи и напряжения. В этом случае расчеты будут
подобны расчету нелинейных цепей постоянного тока, но придется ис-
пользовать комплексный метод или векторные диаграммы.

96
Если же в цепи есть безынерционные элементы, то токи в них ока-
жутся несинусоидальными. Поэтому подобный подход может быть ис-
пользован лишь при замене реальных несинусоидальных кривых экви-
валентными синусоидами с теми же действующими значениями I и U и
таким углом сдвига фаз
arccos ( ) ,PUI
который бы обеспечивал ту
же активную мощность P. В этом и заключается смысл метода эквива-
лентных синусоид.
В расчетах используются вольт- и фазо-амперные характеристики
элементов (ВАХ и ФАХ), которые можно получить экспериментально
(с помощью амперметра, вольтметра и фазометра или ваттметра). Ино-
гда в качестве эквивалентных синусоид выбирают первые гармоники
тока и напряжения, тогда и в расчет вводятся соответствующие харак-
теристики.
Для упрощения электрических схем можно производить замену по-
следовательно или параллельно включенных элементов одним эквива-
лентным подобно тому, как это делалось в нелинейных цепях постоян-
ного тока.
При последовательном соединении элементов суммируются ком-
плексы падений напряжений на них при
одном токе. ВАХ и ФАХ экви-
валентного нелинейного элемента получаются на основе второго закона
Кирхгофа:
Э
j() j()
Э
()e ()e .
k
I
I
k
UI UI
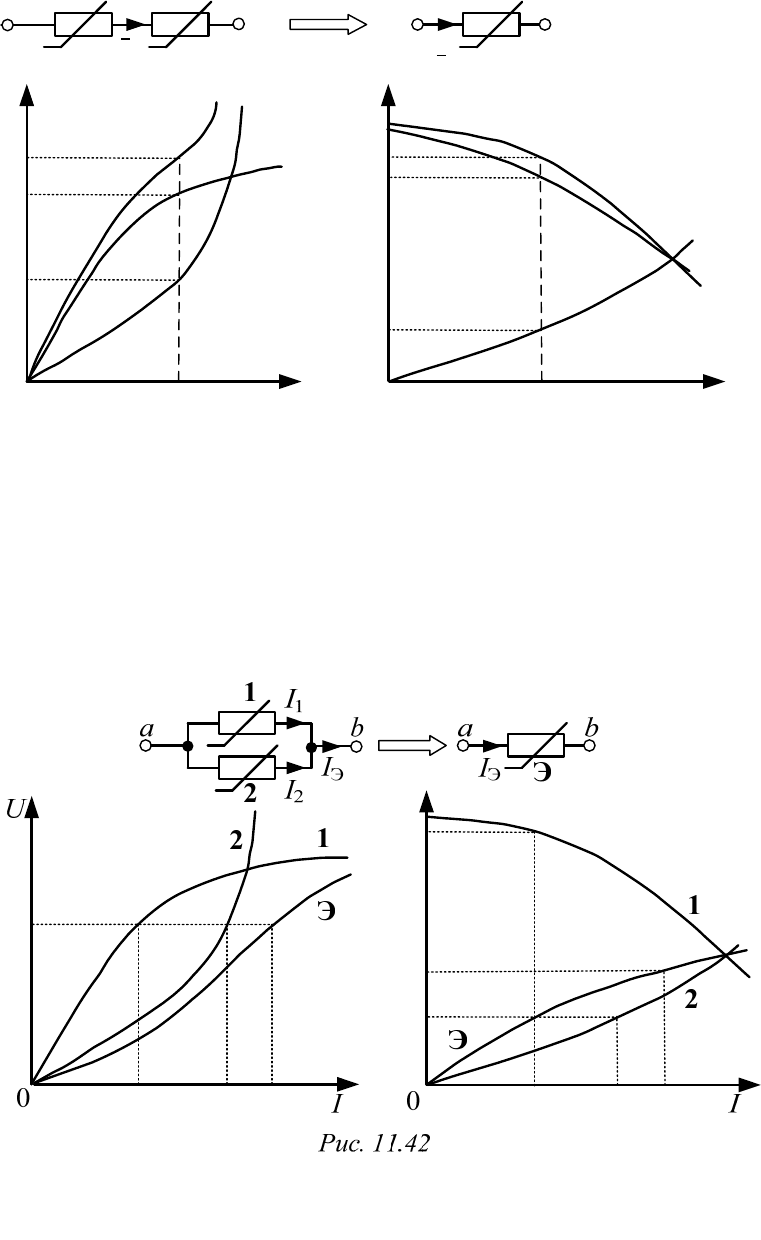
Так, в схеме с двумя элементами (рис. 11.41) следует задаться ка-
ким-либо значением тока, например,
,I
по ВАХ и ФАХ (помечены
цифрами
1 и 2) найти соответствующие ему значения
1
U
,
1
,
2
U
,
2
.
Затем нужно сложить комплексы напряжений на элементах
12
jj
Э 12
ee.UU U
Выделив из результата модуль
ЭЭ
UU
и аргу-
мент
ЭЭ
arg ,U
нанести точки
ЭЭ
(), ()UI I
на графики. Проделав
такую операцию несколько раз и соединив кривыми (помечены бук-
вой
Э) отдельные точки, можно построить характеристики эквивалент-
ного элемента. Если задано напряжение на зажимах цепи и нужно найти
напряжения на отдельных элементах, то сначала по эквивалентной ВАХ
нужно найти ток I, а уже затем по характеристикам элементов – напря-
жения
12
и .UU
Чтобы построить эквивалентные ВАХ и ФАХ при параллельном
соединении, суммируются комплексы токов при одном напряжении в
соответствии с первым законом Кирхгофа
ЭЭ
-j ( ) -j ( )
Э
()e ()e
kk
I
I
k
IU IU
97
и выполняются построения, подобные вышеописанным.
Если проделать такую операцию неоднократно и соединить кри-
выми (
Э) отдельные точки, то будут построены вольт- и фазо-амперная
характеристики эквивалентного элемента.
Пример для схемы с теми же двумя элементами, включенными па-
раллельно, показан на рис. 11.42.
Для определения координат одной из точек на каждой из эквива-
лентных характеристик следует задаться определенным значением
U
и
по ВАХ (
1, 2) найти
12
,.
I
I
Затем по ФАХ (1, 2) нужно определить со-
Рис. 11.41
a
b
ab
I
U
0
I
I
Э
I
0
2
U
1
U
I
I
1
2
1
2
1
2
Э
Э
Э
U
2
Э
1
1
I
2
I
Э
I
U
1
I
2
I
Э
I
2
Э
1
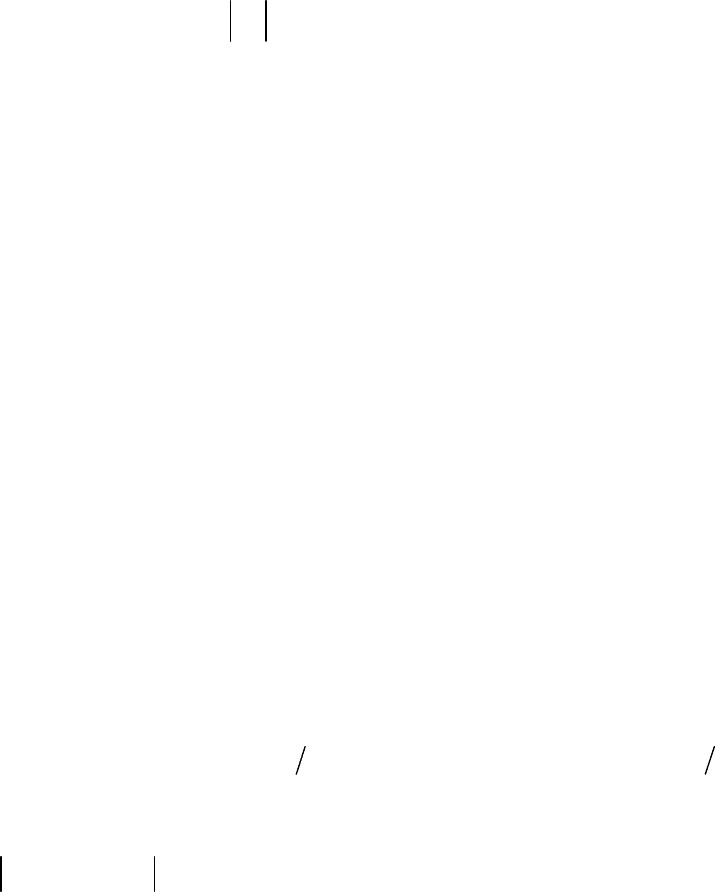
98
ответствующие этим токам значения
12
и .
Потом придется под-
считать комплекс
12
jj
Э 12
,IIе I е
выделить из него аргумент
ЭЭ
arg I
и модуль
ЭЭ
,
I
I
после чего нанести точки
Э
UI
и
ЭЭ
I
на соответствующие графики.
Для расчета упрощенной схемы может применяться метод после-
довательных приближений. Разумеется, все вычисления в этом случае
выполняются в комплексной форме. Метод эквивалентных синусоид,
как показывает опыт, дает неплохие результаты, если, конечно, целью
исследования не является изучение гармонического состава кривых то-
ков и напряжений.
11.5.6. Резонансные явления в нелинейных цепях
Эти явления протекают иначе, чем в линейных цепях, поскольку
параметры нелинейных элементов зависят от режима работы. Измене-
ния режима могут приводить к нарушению условия резонанса или,
наоборот, к его возникновению. При этом возможны неустойчивые со-
стояния и скачкообразные изменения величин.
Чаще всего нелинейность резонансной цепи обусловлена наличием
в ней катушки с
ферромагнитным сердечником. Отсюда и название яв-
ления – феррорезонанс. Анализ его с учетом несинусоидальности кри-
вых весьма сложен, поэтому для знакомства с явлением феррорезонанса
воспользуемся методом эквивалентных синусоид и ограничимся рас-
смотрением простейших случаев.
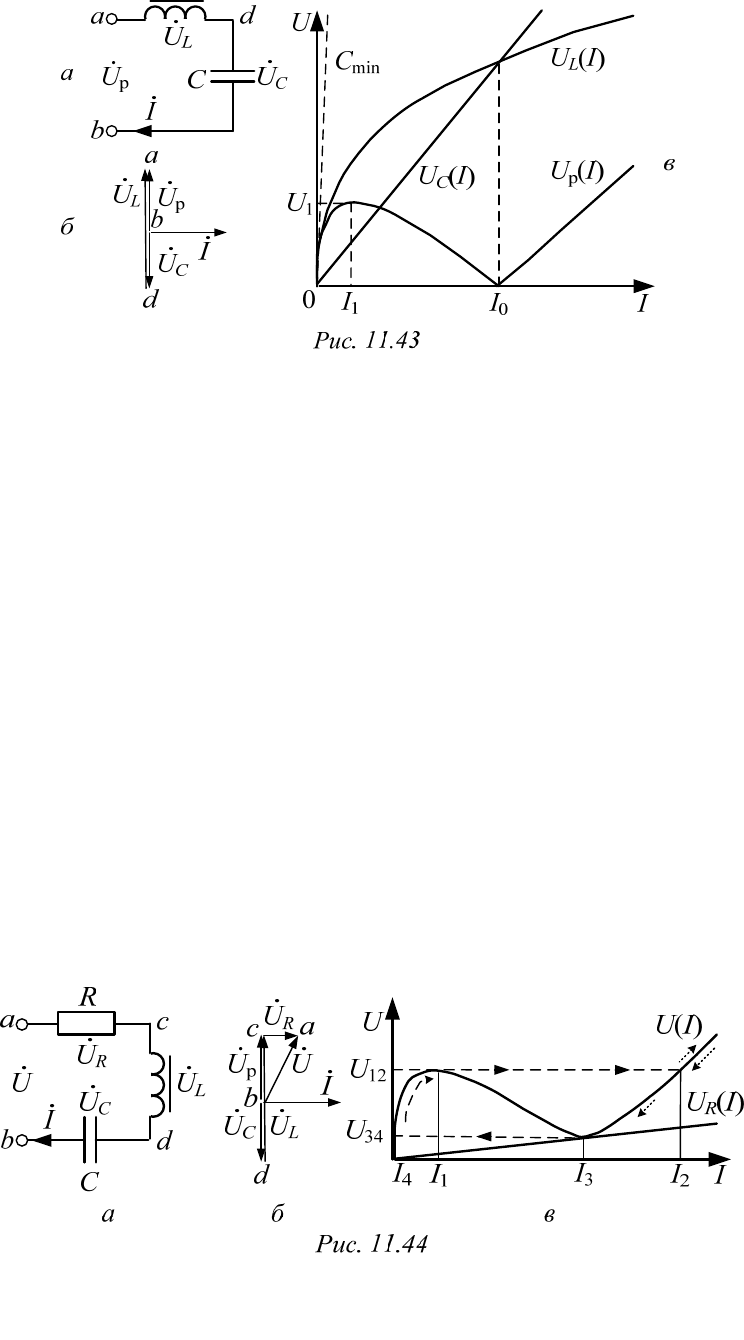
На рис. 11.43, а изображена схема с последовательным соединением
нелинейной индуктивности
(2)
и линейной емкости
(2).
На рис. 11.43, б показана векторная диаграмма, а на рис. 11.43, в – ВАХ
элементов. Если принять
,II
то по второму закону Кирхгофа
р
j()j () .
L С
UI UI Х I
Поэтому для построения эквивалентной вольт-
амперной характеристики цепи на графике при одном токе нужно вычи-
тать напряжения и, взяв модуль результата, строить кривую
р
().UI
При
токе
0
I
напряжения на индуктивности и емкости взаимно компенсиру-
ются, поэтому в данном случае речь идет о феррорезонансе напряжений.
Правда, точка пересечения кривой
()
L
UI
и прямой
()
C С
UI
Х
I
суще-
ствует только в том случае, если
min
,CC
характеристика которой
представляет собой касательную к кривой
()
L
UI
в начале координат.
99
При токах меньших, чем
0
,
L
C
I
UU
и угол сдвига фаз между
входными током и напряжением положителен, при токах больших,
чем
0
,
CL
I
UU
и угол сдвига фаз – отрицателен.
Обратим внимание на неоднозначность характеристики
р
()UI
при
напряжениях
р 1
.UU
Здесь каждому значению
р
U
соответствуют три
значения I (при
р 1
UU
два значения). Причем на падающем участке
характеристики
10
III
положительному изменению тока соответ-
ствует отрицательное изменение напряжения, это говорит о неустойчи-
вости режима работы цепи на этом участке.
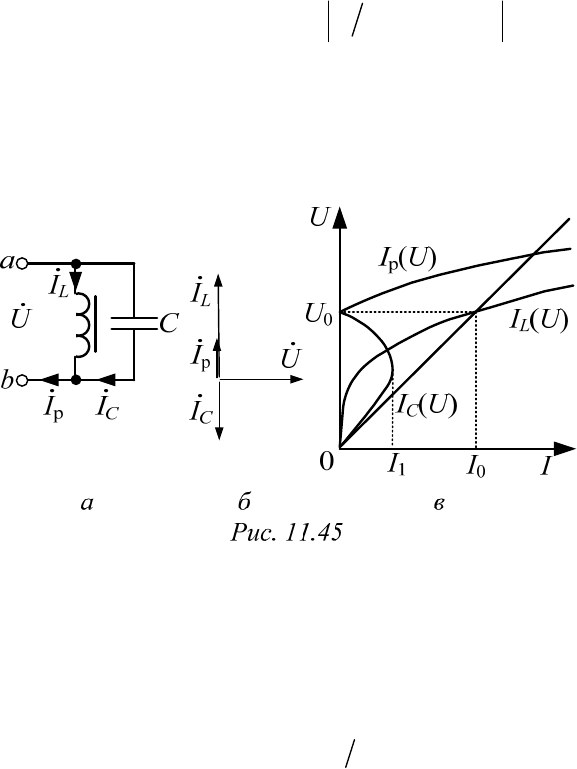
Если учесть активные потери в катушке постоянным сопротивле-
нием R (схема на рис. 11.44, а, векторная диаграмма – на рис. 11.44, б),
то результирующее напряжение найдется из формулы
222
a р
.UUU
Реактивная составляющая
р
U
найдена выше, а активная определяется
законом Ома:
а
.
R
UU RI
Вольтамперная характеристика такой цепи
U(I) построена на рис. 11.44, в.
100
Эту зависимость можно получить экспериментально лишь при пи-
тании цепи от источника тока, плавно изменяя его задающий ток. Если
же плавно увеличивать напряжение на входе цепи, то при достижении
значения
12
U
(максимум кривой U(I)) произойдет скачок тока с
1
I
до
2
I
при одновременном изменении знака угла сдвига фаз.
Если плавно уменьшать напряжение U, то при достижении значе-
ния
34
U
(минимум кривой) произойдет новый скачок тока с
3
I
до
4
I
и
обратное изменение знака угла
. Разумеется, угол меняется тоже скач-
ком – происходит так называемое опрокидывание фазы. Все эти явления
также входят в понятие феррорезонанса напряжений, хотя взаимная
компенсация напряжений на индуктивности и емкости происходит
лишь при вполне конкретном значении тока и соответствующего ему
напряжения.
Аналогичные соображения можно высказать и по поводу схем и
графиков феррорезонанса
токов. Ток на входе схемы без потерь
(рис. 11.45, а) при
UU
определяется по первому закону Кирхгофа.
Как видно из рис. 11.45, б,
p
j() j ().
CL
I
UUXIU
Поэтому эквива-
лентная ВАХ находится вычитанием токов при одном напряжении (по
модулю – рис. 11.45, в). Эта зависимость неоднозначна при токах мень-
ших, чем
1
I
.
Если учесть потери в катушке добавлением в схему замещения парал-
лельного сопротивления R (схема на рис. 11.46, а, векторная диаграмма
на рис. 11.46, б), результирующий ток можно найти из выражения
222
ар
.
I
II
Здесь реактивная составляющая тока
2
р
I
найдена, как пока-
зано выше, а активная – по закону Ома:
а
R
I
IUR
